Some Comments About Guessing

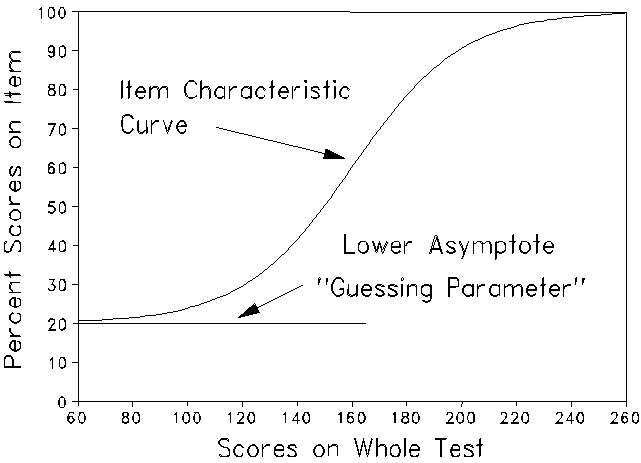
When low scoring persons are found to succeed more often on a multiple choice item than the performance of high scoring persons would imply, a suspicion of guessing on that item is often aroused. In a plot of percent scores on that item versus scores on the whole test, this situation appears as an ogive the left lower tail of which does not asymptote toward zero but rather to some greater value such as 20%.

It is tempting to accept this empirical asymptote as an estimate of the item's "guessing parameter". The trouble is that the credibility of that estimate requires the assumption that the tendency to guess on this item is entirely a quality of the item which has exactly the same fixed effect on all persons. But we know from personal experience as well as research that persons vary in their tendency to guess. Some persons guess a lot, some a little, and some hardly ever. Research into who guesses usually shows that only a small proportion of persons do much guessing. This means that the asymptote observed depends on who has been sampled at this score level and that the value of this asymptote must be expected to vary from sample to sample. Attempts to extract an item characteristic that will be invariant with sampling are doomed, as studies of item "guessing" parameters show.

What can be done about this problem? We can make an effort to avoid the occurrence of guessing by taking care to keep the items we ask persons at their ability levels. This is what tailored testing attempts, and, when it works, guessing disappears.

There is another approach which can help when we have asked persons an item so difficult for them that we have provoked them into guessing. The particular low-scoring persons, whose lucky guesses on items too hard for them have prevented the left lower asymptote of the item characteristic curve from approaching zero, can be identified and dealt with. We can use their low scores as indications of their low abilities and we can use the item's low score as an indication of its high difficulty. From these data we can calculate the probability that persons of this ability would succeed on items of this difficulty.

Since, by definition, a lucky guess is an unexpected, i.e., improbable, right answer, we have found exactly the persons who have done the lucky guessing and thus interfered with the expected item characteristic curve.

This not only allows us to remove lucky guesses from the data and thus obtain an estimate of item difficulty unspoiled by lucky guessing. It also allows us to find and correct person scores that have become exaggerated by extra right answers due to lucky guessing rather than ability.

Some comments about guessing. Wright BD. … Rasch Measurement Transactions 1:2 p.9

Some comments about guessing. Wright BD. … Rasch Measurement Transactions, 1988, 1:2 p.9

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt12a.htm

Website: www.rasch.org/rmt/contents.htm