Communicating Examinee Measures as Expected Ratings

In rating scale analysis, logit measures are a better basis for statistical inference than the original rating scale categories, but the rating scale categories may be a better basis for communication. Content experts and end-users have often internalized the meaning of each rating scale category, so that they know immediately what a "2" or a "6"implies to them in terms of performance. With experience, they can even recognize a "2.5" or a "3.3". Consequently, users may request that a logit measure be converted back onto the rating scale metric for interpretability.

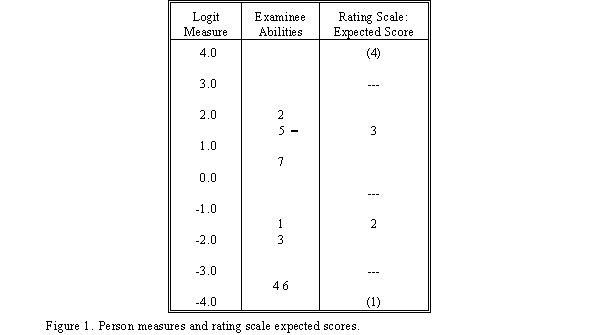
When all items employ the same rating scale, and the mean item difficulty is set to zero (and also judge severity, task challenge, etc.), then a rating scale value corresponding to any person measure can be obtained directly from the generic expected score curve. The Facets computer program provides this, reporting it is as the "Fair Average"rating. This Fair Average can also be obtained by inspection directly from graphical output. In Figure 1, the Fair Average for student 5 (with a measure of 1.5 logits) is at 3.0 on the rating scale metric.

Approximating the Rating Scale Curve

Approximating the rating scale expected score curve (model item characteristic curve) with a logistic ogive aids understanding and simplifies arithmetical operations when performing logit-measure to rating-metric conversions.

A typical Rasch performance assessment model is:

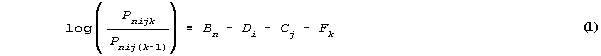
where B_n is the ability of person n; D_i the difficulty of item i; C_j the severity of judge j; F_k the impediment to being observed in category k relative to category k-1; P_nijk is the probability of being observed in category k; and P_nij(k-1) in category k-1.

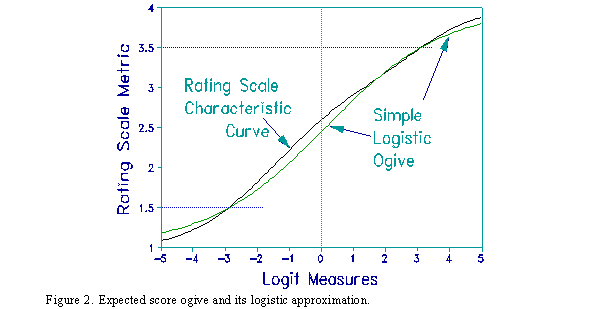
Exact computation of the rating scale characteristic curve is arduous and error-prone. The curve, however, can be usefully approximated with a simple logistic curve with two parameters, one for location and one for slope. The close relationship between the Rasch characteristic curve and a logistic approximation is shown in Figure 2.

Estimating Logistic Parameters

Inspect the output of your Rasch analysis program.

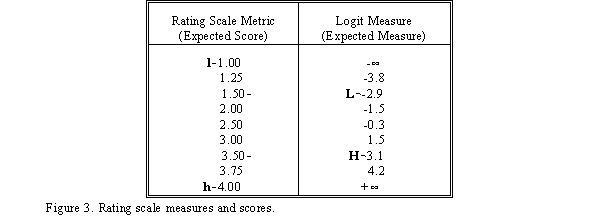
Identify the rating scale parameters (e.g., Table 3 in BIGSTEPS, Table 8 in Facets). Figure 3 is a typical example. Plotting the category scores against the expectation measures produces the rating scale characteristic curve shown in Figure 2.

A logistic approximation is:

where B is the examinee's measure, s is the corresponding value on the rating scale metric; l is the bottom category(1 in the example) and h is the top category (4 in the example); X is a slope parameter and M is a location parameter. The corresponding explicit form for s is:

A serviceable value for X can be estimated from the output of a Rasch calibration program. Decide the range of the expected score curve you wish to match. In this example, I've decided to match the curve along as much of its useful range as possible. In particular, I've chosen to have exact agreement at the points corresponding to expected scores of 1.5 and 3.5. The measure corresponding to 1.5 is -2.9, labeled L, that corresponding to 3.5 is 3.1 labeled H. Then, we have two simultaneous equations using the two points:

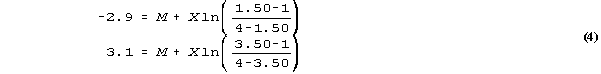
yielding M = 0.1, X = 6/(2*ln(5)) = 1.9.

What Measure corresponds to an Expected Rating of 3?

In equation 2,

B = 0.1 + 1.9log[(3-1)/(4-3)]) = .1 + 1.9log(2) = 1.4, which approximates the reported estimate of 1.5.

What Expected Rating corresponds to a Measure of -1.5?

In equation 3,

which approximates the reported value of 2.0.

Estimating the Effect of Items and Judges

The difference between the expected rating and the average observed rating can be used to compute the effect of the item difficulties and judge severities on the examinee measure. The reported measure has been adjusted for item difficulty and judge severity and so corresponds to the expected rating. The observed average rating (Obs Avge)includes a context effect due to the particular items and judges encountered by the examinee. An observed measure corresponding to the observed average rating can be computed using the logistic approximation:

where B_Obs is the measure based on the Observed Average. Then the impact of the context on the measure is

How much impact has context had on a examinee's measure?

Here is one examinee from a Facets report, using the same 4 category rating scale as before:

--------------------------------------
|Obsvd  Obsvd  Obsvd   Fair    Logit |
|Score  Count Average Average Measure|
--------------------------------------
|  87     15     2.8   3.0     1.51  |
--------------------------------------

This examinee's reported measure is 1.51 logits. The Fair Average (expected rating) is 3.0 rating points. According to the logistic approximation, the measure corresponding to 3.0 is 1.4, which is close to the reported measure of 1.51, as expected.

The observed score is 87 from 15 observations, producing an observed average of 2.8 as shown. The observed measure, B_Obs, is, by the logistic approximation,

Thus, the effect of the examination context (of more severe than average judges and/or more challenging than usual items) is to make this examinee appear to perform 1.51 - 0.9 = .6 logits worse than in a standard situation.

John Michael Linacre

Communicating Examinee Measures as Expected Ratings. Linacre J. M. … Rasch Measurement Transactions, 1997, 11:1 p. 550-551.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt111m.htm

Website: www.rasch.org/rmt/contents.htm