The Hierarchical Rater Model from a Rasch Perspective

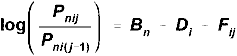
Modeling rater behavior is problematic. Are the rater's intended to be acting as locally-independent experts, each with a unique perspective of what is the "true" rating? If so, each rater provides new information about the person being rated. The raters have the same status as test items, and a many-facet Rasch model is indicated. In general, more ratings by more raters of the same person-item interaction produce more measurement information.

Are the raters merely human scoring machines, all expected to produce the same one, "true" rating? If so, then the same type of quality control that would be applied to optical scanning equipment is indicated. More ratings by more raters of the same person-item interaction produce no additional measurement information, nor more information about the "true" rating.

In practice, however, the situation is ambivalent. Raters are told to use their expertise, but are also instructed to conform with other raters in awarding "true" ratings. More ratings by more raters of the same person-item interaction produce more information about the "true" rating, but not otherwise more measurement information about the performance.

So how is this asymmetry in the rating process to be modeled? The Hierarchical Rater Model (HRM) is one approach.

HRM (Patz et al., 2000, a variant is Donoghue & Hombo, 2003) uses a two-level approach. At the first level is modeling person performance. HRM uses a Rasch Partial Credit Model with persons and items, but the estimates are based on idealized "true" (not empirical) ratings.

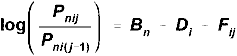
where "j" represents "true", not empirical, ratings.

At the second level are the idealized "true" ratings. HRM models each rater's empirical ratings to follow a normal distribution on a "raw rating" variable. Somewhere on this treated-as-linear variable is the "ideal" or "true category" rating, i.e., the rating that would have been awarded by a perfect rating machine to a particular person on a particular item.

Each empirical rating, however, is displaced from its corresponding ideal by
(a) its rater r's leniency, μ_r, expressed as a fractional-raw-score rating adjustment, and
(b) its rater r's unreliability, expressed as the fractional-raw-score standard deviation, σ_r, of a normal distribution around the rater's severity.

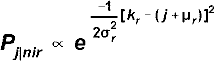
where j is the ideal "true" rating of person n on item i and k is the empirical rating observed for rater r.

Donoghue & Hombo differ from Patz et al. in using the generalized partial credit model (i.e., the Rasch partial credit model with an item discrimination parameter) and a "fixed effect" rating model (not completely specified in their paper).

From a Rasch perspective, using the "partial credit" model is impeccable. The "ideal" rating model, however, is deficient. The "raw rating" variable is definitely not interval, it is ordinal, and may only be dichotomous. For a very lenient rater on a long rating scale, the most probable rating, according to HRM, could be a category above the top of the scale. This is impossible, so an adjustment must be made. Most obviously, the probability of awarding categories above the top category should be added to the probability of the top category. But this does not appear to have been done. Instead, out- of-range categories are merely ignored. The effect of this is that lenient raters are estimated to be even more lenient, and vice-versa for severe raters.

This suggests that an immediate improvement to the HRM model would be to express the "idealized rating" model in logistic terms, e.g., most simply,
log_e ((x-"bottom")/("top"-x)),
where "bottom" and "top" are the extreme categories.

The probability of observing any particular category then becomes the integral of the probabilities of the rating occurring within 0.5 rating-points of that category on the logistic rating variable. A further improvement (perhaps already made by Patz or Donoghue) would be to bring into the "partial credit" model not merely the "idealized rating" for each person-item confluence, but the set of all possible ratings, and the probability that each one is ideal.

This area of research is at an early stage. Here is an opportunity for a Rasch-oriented doctoral student to formulate a truly measurement-based HRM model.
John Michael Linacre

Patz R.J., Junker B.W., Johnson M.S. (2000) The Hierarchical Rater Model for Rated Test Items and its Application to Large-Scale Educational Assessment Data. Revised AERA Paper.

Donoghue J.R., Hombo C.M. (2003) An Extension of the Hierarchical Raters' Model to Polytomous Items. NCME Paper.

The Hierarchical Rater Model HRM from a Rasch perspective. J.M. Linacre, R.J. Patz, J.R. Donoghue … 17:2 p. 928

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt172k.htm

Website: www.rasch.org/rmt/contents.htm