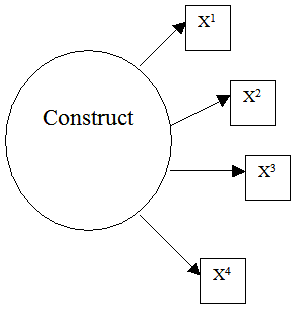
Reflective
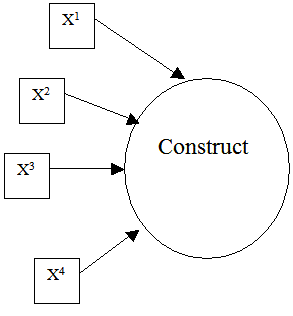
Formative
Structural equation modeling (SEM) distinguishes two measurement models: reflective and formative (Edwards & Bagozzi, 2000). Figure 1 contrasts the very different causal structure hypothesized in the two models. In a reflective model (left panel), a latent variable (e.g., temperature, reading ability, or extraversion) is posited as the common cause of item or indicator behavior. The causal action flows from the latent variable to the indicators. Manipulation of the latent variable via changing pressure, instruction, or therapy causes a change in indicator behavior. Contrariwise, direct manipulation of a particular indicator is not expected to have a causal effect on the latent variable.

Reflective |

Formative |
| Figure 1. Causal Structures. | |
A formative model, illustrated on the right-hand side of Figure 1, posits a composite variable that summarizes the common variation in a collection of indicators. A composite variable is considered to be composed of independent, albeit correlated, variables. The causal action flows from the independent variables (indicators) to the composite variable. As noted by Bollen and Lennox (1991), these two models are conceptually, substantively, and psychometrically different. We suggest that the distinction between these models requires a careful consideration of the basis for inferring the direction of causal flow between the construct and its indicators.
Given the primacy of the causal story we tell about indicators and constructs, what kind of experiment, data, or analysis could differentiate between a latent variable story and a composite variable story? For example, does a Rasch analysis or a variable map or a set of fit statistics distinguish between these two different kinds of constructs? We think not! A Rasch model is an associational (think: correlational) model and as such is incapable of distinguishing between the latent-variable-causes-indicators story and the indicators-cause-composite-variable story.
Some examples from without and within the Rasch literature should help illustrate the distinction between formative and reflective models. The paradigmatic example of a formative or composite variable is socioeconomic status (SES). Suppose the four indicators are education, occupational prestige, income, and neighborhood. Clearly, these indicators are the causes of SES rather than the reverse. If a person finishes four years of college, SES increases even if where the person lives, how much they earn, and their occupation stay the same. The causal flow is from indicators to construct because an increase in SES (job promotion) does not imply a simultaneous change in the other indicators. Bollen and Lennox (1991) gave another example: life stress. The four indicators are job loss, divorce, recent bodily injury, and death in the family. These indicators cause life stress. Change in life stress does not imply a uniform change in probabilities across the indicators. Lastly, the construct could be accuracy of eyewitness identification and its indicators could be recall of specific characteristics of the person of interest. These characteristics might include weight, hair style, eye color, clothing, facial hair, voice timber, and so on. Again, these indicators cause accuracy; they are not caused by changes in the probability of correct identification.
The examples of formative models presented above are drawn from the traditional classical test theory (CTT), factor analysis, and SEM literatures. Are Rasch analyses immune to confusion of formative and reflective models?
Imagine constructing a reading rating scale. A teacher might complete the rating scale at the beginning of the school year for each student in the class. Example items (rating structure) might include: (1) free or reduced price lunch (1,0), (2) periodicals in the home (0,1,2,3), (3) daily newspaper delivered at home, (4) student read a book for fun during the previous summer (1,0), (5) student placement in reading group (0,1,2,3), (6) student repeated a grade (1,0), (7) students current grade (1,2,3,…), (8) English is student's first language (1,0), and so on. Now, suppose that each student, in addition to being rated by the teacher, took a Lexile-calibrated reading test. The rating scale items and reading test items could be jointly analyzed using WINSTEPS or RUMM2020. The analysis could be anchored so that all item calibrations for the reading rating items would be denominated in Lexiles. After calibration, the best-fitting rating scale items might be organized into a final scale and accompanied by a scoring guide that converts raw counts on the rating scale into Lexile reader measures. The reading scale is conceptually a composite formative model. The causal action flows from the indicators to the construct. Arbitrary removal of two or three of the rating items could have a disastrous effect on the predictive power of the set and, thus, on the very definition of the construct, whereas, removal of two or three reading items from a reading test will not alter the construct's definition. Indicators (e.g., items) are exchangeable in the reflective case and definitional in the formative case.
Perline, Wainer, and Wright (1979), in a classic paper, used parole data to "measure a latent trait which might be labeled 'the ability to successfully complete parole without any violations'" (p. 235). Nine dichotomously scored items rated for each of 490 participants were submitted to a BICAL analysis. The items were rated for presence or absence of: high school diploma or GED, 18 years or older at first incarceration, two or less prior convictions, no history of opiate or barbiturate use, release plan to live with spouse or children, and so on. The authors concluded, "In summary, the parole data appeared to fit [the Rasch Model] overall. . . . However, when the specific test for item stability over score groups was performed . . . there were serious signs of item instability" (p. 249). For our purposes, we simply note that the Rasch analysis was interpreted as indicating a latent variable when it seems clear that it is likely a composite or formative construct.
A typical Rasch analysis carries no implication of manipulation and thus can make no claim about causal action. This means that there may be little information in a traditional Rasch analysis that speaks to whether the discovered regularity in the data is best characterized as reflective (latent variable) or formative (composite variable).
Rasch models are associational (i.e., correlational) models and because correlation is necessary but not sufficient for causation, a Rasch analysis cannot distinguish between composite and latent variable models. The Rubin-Holland framework for causal inference specifies: no causation without manipulation. It seems that many Rasch calibration efforts omit the crucial last step in a latent variable argument: that is, answering the question, "What causes the variation that the measurement instrument detects?" (Borsboom, 2005). We suggest that there is no single piece of evidence more important to a construct's definition than the causal relationship between the construct and its indicators.
A. Jackson Stenner, Donald S. Burdick, & Mark H. Stone
Bollen, K. A., & Lennox, R. (1991). Conventional wisdom on measurement: A structural equation perspective. Psychological Bulletin, 100, 305-314.
Borsboom, D. (2005). Measuring the Mind. Cambridge, MA: Cambridge University Press.
Burdick, D. S., Stone, M. H., & Stenner, A. J. (2006). The combined gas law and a Rasch reading law. Rasch Measurement Transactions, 20(2), 1059-1060.
Edwards, J. R., & Bagozzi, R. P. (2000). On the nature and direction of relationships between constructs and measures. Psychological Methods, 5, 155-174.
Perline, R., Wainer H., & Wright, B. D. (1979). The Rasch model as additive conjoint measurement. Applied Psychological Measurement, 3(2), 237-255.
Formative and Reflective Models: Can a Rasch Analysis Tell the Difference? A. Jackson Stenner, Donald S. Burdick, & Mark H. Stone … Rasch Measurement Transactions, 2008, 22:1 p. 1152-3
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| May 17 - June 21, 2024, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 12 - 14, 2024, Wed.-Fri. | 1st Scandinavian Applied Measurement Conference, Kristianstad University, Kristianstad, Sweden http://www.hkr.se/samc2024 |
| June 21 - July 19, 2024, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 5 - Aug. 6, 2024, Fri.-Fri. | 2024 Inaugural Conference of the Society for the Study of Measurement (Berkeley, CA), Call for Proposals |
| Aug. 9 - Sept. 6, 2024, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Oct. 4 - Nov. 8, 2024, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Jan. 17 - Feb. 21, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| May 16 - June 20, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 20 - July 18, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com |
| Oct. 3 - Nov. 7, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt221d.htm
Website: www.rasch.org/rmt/contents.htm