Old Rasch Forum - Rasch on the Run: 2008
Rasch Forum: 2006
Rasch Forum: 2007
Rasch Forum: 2009
Rasch Forum: 2010
Rasch Forum: 2011
Rasch Forum: 2012
Rasch Forum: 2013 January-June
Rasch Forum: 2013 July-December
Rasch Forum: 2014
Current Rasch Forum
161. Using RASCH to determine uni-dimensionality
pjiman1 June 18th, 2008, 8:22pm:
Greetings Mike
I really appreciate your assistance in the past.
I have questions about determining uni-dimensionality.
From what I read on the boards there are a couple of rules of thumb for dimensionality.
Background:
I am in the field of social and emotional competencies. In general, it is not surprising to see the same construct either defined in different ways, multiple constructs with similar items, or constructs with overlapping definitions. For example, what is the difference between self-control, self-management, self-discipline? In my opinion, it appears that different operationalizations of a construct are used depending on the lens that a research adopts. Self-control is usually talked about when discussing anger outbursts, self-management is sometimes defined as handling stress, controlling impulses, and motivating oneself to persevere in overcoming obstacles to goal achievement, etc. In some ways, the overlap among these constructs is fine, as long as the purpose of the construct is clear.
RASCH assumes uni-dimensionality of the measure, not of the data (i.e. the person's responses). Uni-dimensionality of the measure is cleaner for interpretation. However, from what I gathered, it is not possible to prove that a measure is uni-dimensional, but we can gather enough evidence to argue that a measure is uni-dimensional.
Is the following correct - RASCH is concerned with establishing the uni-dimensionality of the measure. That means that RASCH will determine if a set of items is measuring one math skill.
I have a measure of social-emotional constructs for the lower elementary grades. It has 19-items, each item is scored yes or no. It is a student self-report measure. Higher scores indicate higher levels of the social-emotional construct. There are several constructs being measured, and (unfortunately) 1 or 2 items per domain of social and emotional construct. N = 1571
I am trying to establish the uni-dimensionality of the measure. The findings are:
SUMMARY OF MEASURED (NON-EXTREME) Persons
+-----------------------------------------------------------------------------+
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 33.4 18.6 1.94 .73 1.00 .1 .94 .1 |
| S.D. 3.4 1.2 1.06 .19 .27 .8 .72 .8 |
| MAX. 37.0 19.0 3.50 1.57 2.05 3.2 9.54 3.4 |
| MIN. 7.0 4.0 -1.71 .53 .21 -2.3 .14 -1.9 |
|-----------------------------------------------------------------------------|
| REAL RMSE .79 ADJ.SD .71 SEPARATION .90 Person RELIABILITY .45 |
|MODEL RMSE .75 ADJ.SD .75 SEPARATION 1.00 Person RELIABILITY .50 |
| S.E. OF Person MEAN = .03 |
+-----------------------------------------------------------------------------+
SUMMARY OF 19 MEASURED (NON-EXTREME) Items
+-----------------------------------------------------------------------------+
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 2765.1 1541.4 .00 .08 .99 .1 .94 -.1 |
| S.D. 242.0 9.8 1.22 .03 .07 1.9 .23 2.7 |
| MAX. 3058.0 1554.0 2.43 .15 1.11 4.7 1.29 4.5 |
| MIN. 2170.0 1514.0 -2.08 .06 .89 -2.2 .53 -3.2 |
|-----------------------------------------------------------------------------|
| REAL RMSE .09 ADJ.SD 1.22 SEPARATION 13.55 Item RELIABILITY .99 |
|MODEL RMSE .09 ADJ.SD 1.22 SEPARATION 13.66 Item RELIABILITY .99 |
| S.E. OF Item MEAN = .29 |
+-----------------------------------------------------------------------------+
One rule - MnSq is not a good indicator of deviation from uni-dimensionality, so the findings here will not help me. Although, the extremely low person separation and reliability figures are worrisome.
Second rule - Principal contrasts are better for examining dimensionality.
STANDARDIZED RESIDUAL VARIANCE SCREE PLOT
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
Empirical Modeled
Total variance in observations = 38.7 100.0% 100.0%
Variance explained by measures = 19.7 50.9% 48.9%
Unexplained variance (total) = 19.0 49.1% 100.0% 51.1%
Unexplned variance in 1st contrast = 1.8 4.8% 9.7%
Unexplned variance in 2nd contrast = 1.4 3.5% 7.1%
Unexplned variance in 3rd contrast = 1.2 3.2% 6.5%
Unexplned variance in 4th contrast = 1.2 3.0% 6.1%
Unexplned variance in 5th contrast = 1.1 2.9% 5.9%
The unexplained variance is practically equal to variance explained. That seems to indicate that there is a lot of noise in this data, not necessarily the measure. Is this a correct interpretation?
Third rule - I should examine the contrasts and a size of 2.0 and a noticeable ratio of first contrast to measure-explained variance. The ration is 4.8 to 50.8 = .09. This seems good.
I assume that contrast refers to the eigenvalue is this correct? If so the eigenvalue of the first contrast is 1.8. Using a horseshoes and in grenades viewpoint, this value sounds like it be cause for concern that there is multi-dimensionality.
Fourth rule - at least 40% variance in the explained and less than 20% in the next component. The output above clearly meets this criteria.
Fifth rule - examine the cluster of contrasting items for change. I viewed the contrast loadings for the 1st contrast and the second contrast. At the strictest level, there is change in the item clusters. At a relaxed level, some of the items are clustered, some are not. Overall there does appear to be change.
Final rule - does the degree of multi-dimensionality matter? are the differences important enough that the measure has to be separated into two measures?
In my case, it is not uncommon for social and emotional constructs to be conceptually related to each other. Just like a story math problem employs both math and reading skills, positive social relationships involves successful management of emotions. So perhaps the degree of multi-dimensionality does not matter in my case.
Moreover, I did a confirmatory factor analysis of the scale. A one factor model did not fit the data. After tinkering, a three factor model did fit, but with interfactor correlations of .42, .48, .70, which suggests to me that a multi-factor model fits the data and that the factors are related to each other. The exploratory factor analysis did suggest that a one-factor solution was clearly not present and that a 2 or 3 factor solution was more viable.
As I think about this, factor analysis examines the multi-dimensionality of the data, whereas RASCH examines multi-dimensionality of the measure. So it should not be surprising that factor analysis and RASCH dimensionality analysis do not converge because they are examine dimensionality in different ways. In fact, if a person does fit the measure, person measure will likely show up as a misfit rather than as possible evidence that the measure is multi-dimensional. Am I correct?
So after all this, my conclusion is that while there may be multiple factors in the data, from a measurement perspective, it is a one-dimensional measure. It is simpler to analyze and use the measure as a single dimension and I have enough RASCH support to back my conclusion.
However, the greater point in my case is the poor person separation and reliability and I need to go back to the drawing board to get better person measures. Additional, self-report of social and emotional constructs at the early elementary student level are generally known to be difficult, so I might end up scrapping this effort.
Am I correct?
Thanks for wading through this.
Pjiman1
MikeLinacre:
Thank you for your post and your questions, Pjiman1. Very perceptive!
Strictly unidimensional data do not exist in the empirical world. Even straight lines have widths as soon as we draw them.
So a central question is "How close to unidimensional is good enough for our purposes?"
For an arithmetic test, the administrators are happy to combine addition, subtraction, multiplication, division into one measure. But a diagnostician working with learning difficulties may well consider them four different dimensions of mental functioning, producing four different measures.
But statistics can be helpful in making decisions about multidimensionality.
1a. Mean-squares. You are correct.Individual item and person fit statistics are usually too much influenced by local accidents in the data (e.g., lucky guesses) to be strongly indicative of secondary dimensions.
1b. Low reliability. Not indicative of multidimensionality, but indicative of either a test that has too few items for your purposes (only 19), or a sample with not enough performance spread.
2. Unexplained variance = Explained variance. Again an indication of narrow spread of the measures. The wider the spread of the measures, the more variance explained. Not an indicator of multidimensionality.
3. Simulation studies indicate that, for data generated to fit a Rasch model, the 1st contrast can have an eigenvalue of up to 2. This is 2-items strength. A secondary "dimension" with a strength of less than 2 items is very weak.
4. These percents may apply to someone's data, but in general the "Modeled" column tells you what would happen in your data if they fit the Rasch model perfectly. In fact your measures appear to be over-explaining the variance in the data slightly (50.9% vs. 48.9%), suggesting that the data are in some way constrained (not enough randomness), e.g., by a "halo effect" in the responses.
5. Look at the 1st Contrast. Compare the items loading one way (at the top) against the items loading the other way (at the bottom). Is the substantive difference between the items important? This would be the first sub-dimension in the data. If it is important, act on it.
If the 1st Contrast is important, then the second contrast may be worth inspecting etc.
6. "does the degree of multi-dimensionality matter?" - The crucial question. One way is to divide the items into two instruments, one for each sub-dimension. Estimate the person measures and cross-plot them. Does the difference in the person measures matter? (Remember that the standard errors of your "split" person measures will be large, about 1.1 logits).
You concluded: "I need to go back to the drawing board to get better person measures."
Assuming your person sample are representative, then your instrument needs more items and/or your items need longer rating scales (more categories).
If you doubled the length of the instrument from 19 to 38 items, then its reliability would increase from about 0.5 to about 0.7. So it does look as though precise measurement at an individual-person level will be difficult to obtain. But your instrument does produce usefully precise measures for group-level reporting.
pjiman1:
Thanks Mike, most helpful.
Two questions:
You stated - "If you doubled the length of the instrument from 19 to 38 items, then its reliability would increase from about 0.5 to about 0.7. So it does look as though precise measurement at an individual-person level will be difficult to obtain. But your instrument does produce usefully precise measures for group-level reporting."
You stated this because the person reliability could probably only go to .7 and concluded that precision at the individual-person level would be difficult to obtain. What value for person reliability or what other output would you need for you to say that precision at the individual person level was achieved?
Second, what RASCH output values did you use to conclude that the instrument has useful precise measures for group-level reporting? I never thought it was possible that an instrument could be useful for group-level reporting but not individual level reporting. What does this mean in a practical sense? What kind of conclusions could I draw from an instrument that has good group-level precision but not individual level precision.
Finally, I am beginning to think that my thinking about dimensionality has a serious flaw because I thought that dimensionality has the same properties in RASCH as it is discussed in a factor model. I originally thought that I should establish dimensionality for a scale by first using a confirmatory factor analysis to see what is the factor structure. Based on the inter-factor correlations, I could determine if each factor in the model is uni-dimensional. I could also explore alternative factor models using exploratory factor analysis and see if there are factors that are uni-dimensional. Based on the factor model, I would have conducted a RASCH analysis on just those items that load on each of the uni-dimensional factors. So if my CFA had a 3 -factor model, and each was uni-dimensional, I would run three separate RASCH models, one for each dimension. Based on this and other discussions, I am starting to think my thinking is wrong. It is an error to think that dimensionality in RASCH has the same properties as in a factor model. So, say my factor model has three factors with moderate intercorrelations, that says nothing about the dimensionality of the measure in the RASCH world and if RASCH says that the measure (not the data) is uni-dimensional, then it is.
I am now beginning to wonder if RASCH analysis and factor analysis should be used in conjunction with each other. I learned about scale analysis using the factor model. Is there any advantage to using the results obtained from a factor analysis to inform the results obtained from a RASCH? Or should RASCH be the only analysis that matters when investigating the measurement properties of a scale?
Thanks again for reading through this as I try to untangle my thoughts on this topic.
pjiman1
MikeLinacre:
Let's see if these answers will help you, Pjiman1.
You asked: "What value for person reliability or what other output would you need for you to say that precision at the individual person level was achieved?"
To reliabily differentiate between high and low performers in your sample, a test needs a reliability of 0.8. If you are only concerned to discriminate between very high and very low performers, than 0.7.
You asked: "Group level reporting".
If we summarize many measures all imprecise, then the summary, e.g., the mean, can have precision much greater than the precision of any of the individual measures. We apply this every time we measure several times and then base our decisions on the average.
You asked: "Factor analysis and Rasch"
CFA or PCA of the original observations are difficult to align with Rasch dimensionality for several reasons. Here are some
1. The original observations are non-linear. This curvature will distort the factor structure.
2. Unevenness in the distributions of persons or items will produce spurious factors, see "Too many factors" www.rasch.org/rmt/rmt81p.htm
3. If you are using rotation or obliqueness in your CFA, then the variance structure is no longer that in the data, so the factor structure will not match the orthogonal, unrotated variance structure in the Rasch analysis.
4. In CFA, some variance is not allocated to the factors. Rasch corresponds more closely to PCA in which all variance is allocated.
pjiman1:
Mike, thank you again for your invaluable comments.
Final question - should factor analysis and RASCH analysis be used in conjunction with each other to examine scale properties? The reason I ask is that most audiences would want to see results from a factor analysis because that is what they are used to seeing. I am starting to think that perhaps I should skip reporting results from a factor analysis and just report RASCH analysis results.
Thanks for letting me ask this final one.
Peter
MikeLinacre:
Communication of our findings is our biggest challenge, Pjiman1.
If your audience is convinced by factor analysis, then please report it.
A basic rule in science is that reasonable alternative methods should produce the same findings. If they don't, then we need to examine whether the findings are really in the data or merely artifacts of the methods. So if Rasch and factor analysis come to different conclusions about the data, then more thought is definitely necessary. Explaining the reasons for the different conclusions could be the most valuable feature of your research report.
pjiman1:
Sounds good to me. THANK YOU!!!
Pjiman1
mve:
Hi. This thread is very useful. From what I understand, simulation studies indicate that eigenvalues less than 1.4 most likely indicats unidimensionality. In my case, the 1st contrast has an eigenvalue of 3.0. Thus, I would like to look at the 1st contrast and compare the items loading one way against the items loading the other way (looking at loading factors greater than +-0.3). Here is where I get stuck. How do you do this? From what I found in previous literature, it seems that you need to do a paired t-test of the person estimates between the positive subset and the person estimates from all items. Then do the same for the negative subsets. If this is correct, my question is: What is it meant by person estimate? Which Winsteps Table will provide me with person estimate values? Sorry if this sounds to obvious but I've been thinking about it and don't seem to find the answer.
Also, when you said estimate the person measures and cross-plot them. How do you do this in Winsteps? Once again, thanks in advance for your help. Marta
MikeLinacre:
Thank you for this question, Marta.
"eigenvalues less than 1.4 most likely indicates unidimensionality"
If the first eigenvalue is much smaller than 1.4, then the data are "too good" (not random enough in a Rasch conforming way). Examine the data to be sure that there is not something else distorting the randomness. For instance, systematic missing data. We expect the first contrast to be somewhere between 1.4 and 2.0.
"I would like to look at the 1st contrast and compare the items loading one way against the items loading the other way"
Yes, the first step is to identify the substantive content of the contrast. What is this contrast? Is it meaningful, or only an accident of the sample? Is it important to you, or is it something you are prepared to ignore? For instance, on a language test, some items will be relatively easier for native-language speakers (e.g., colloquialisms) but other items will be relatively easier for second-language speakers (e.g., words with similarities to their native speakers). This could be the first contrast in the items. Is this "native-second" dimension important? If we are using the language test to screen job applicants, it probably is not. We only want to know "does this person have high or low language proficiency?" But you may decide to add or omit items which favor one group of speakers.
"a paired t-test of the person estimates"
I'm not familiar with this approach, but here's how to do it in Winsteps
You have your positive subset of items and your negative subset of items (two lists).
Edit your Winsteps control file.
Put a "+" sign in column 1 of all the item labels for the positive items
Put a "-" sign in column 1 of all the item labels for the negative items
Put a "#" sign in column 1 of all the other items
Save your control file.
Analyze your control file.
Produce Table 23. You should see all "+" items at one end, the "-" items at the other end, and the "#" items in the middle.
That confirms everything is correct.
1. Paired t-tests for each person in the sample (perhaps a huge list).
Produce Winsteps Table 31 (differential person functioning) specifying column 1 in the item labels (+,-,#). The numbers you want are in Table 31.3
2. Paired t-test for the subsets of measures.
Copy-and-paste the relevant measures from Winsteps Table 31.3 into Excel ("Text to columns" is the Excel function you will probably want to use).
One column for "Baseline Measure", one column for "+ DPF Measure", one column for "- DPF Measure". Instruct Excel to perform paired t-tests on the three columns.
"cross-plot them."
You can cross-plot with Excel, but the Winsteps scatterplot (Plots menu) may be more useful. Perform separate analyses using ISELECT= for the two sets of items. Write out PFILE= person files. Then, in an analysis of all the data, use the Winsteps scatterplot option to cross-plot each PFILE against the person measures for all the items.
Does this meet your needs, Marta?
mve:
Hi Mike! Your reply is exactly what I needed! Thanks a lot for helping me (and others in this forum). Unfortunately, every answer creates further questions... Can I clarify the following points?
1. When dividing the items as "+", "-", or "#", I guess is up to me whether or not to use a cut-off for the loadings (e.g. only consider + those with loadings more than 0.3).
2. When I create the Excel Table with 'Baseline', 'DPF+' and 'DPF-' columns I have some values with maximum or minimum score (e.g. 3.56>). To perform the t-tests I have removed the > or < signs. I guess this will be fine...
3. When we cross-plot with Winsteps, I have written a PFILE= for all the data, another PDFILE when re-running the analysis for ISELECT="-" and another PDFILE for ISELECT="+". Then we compare whether the graphs that we get are similar or not for:
person measures PFIFLE(all) vs PFILE(+)
and
person measures PFILE (all) vs PFILE (-)
If no major differences seen, again it suggests unidimensionality. Is this right?
4. I suppose that if the first contrast suggest unidimensionality, there is no need to further examine the remaining contrasts? In my case there is 19.8 variance explained by measures and 21 unexplained variance (with 5 contrasts).
5. A final question, I understand that the aim of analysing PCA of the residuals is to establish whether the responses to the items of the questionnaire can be explained by the Rasch model or whether there are any further associations between the resiudals (Table 23). However, I can not fully understand the conceptual difference between this analysis and the info that we can get if we ask for Table 24.
Once again, thanks for your help and sorry for being so inquisitive. Marta
MikeLinacre:
Yes, one set of questions leads to another, Marta.
1. "loadings more than 0.3"
Better to look at the plot in Table 23.2 and see how the items cluster vertically. Often there are 2 or 3 outlying items vs. everything else. Then the contrast dimensions is those items vs. everything else. There are no neutral items.
2. "I have removed the > or < signs"
Yes, but these signs warn you that the values next to them are very uncertain.
3. "If no major differences seen, again it suggests unidimensionality"
It really suggests, "if there is multidimensionality, it is too small to have any meaningful impact on person measurement". So, we may see two types of items in the contrast-plot, but their difference, though statistically significant, does not have a substantive impact on person measurement.
4. "there is no need to further examine the remaining contrasts?"
Look at least one more. (Winsteps always reports 5). Sometimes the first contrast is a small effect among many items, but the second contrast is a big effect among a few items. The big effect may be more important to you than the small effect.
5. Table 23 (item dimensionality) and Table 24 (person dimensionality) are looking at the same data (and the same residuals) from different perspectives.
Table 23 is investigating "Are there two or more types of items?"
Table 24 is investigating "Are there two or more types of persons?"
Usually the two interact: one type of person does better on one type of item, but another type of person does better on another type of item.
Since there are usually many more persons than there are items, it is easier to start by looking at the items. Often we can see the dimensionality pattern so clearly from the items that there is no need to look at the persons.
mve:
Mike, Thanks for all your help. I'm working on everything we've recently been discussing. Marta
OlivierMairesse:
Hi fellow Rasch enthusiasts. I've had a nice e-mail conversation with Mike about multidimensionality, CFA, etc. and he agreed to let me publish it on this forum. Hope this helps! It sure helped me.
QUESTION: In a study to determine the factors influencing car purchase decisions, we asked 1200 people to rate how important they find a particular car attribute in their purchase decision. We used 17 items (e.g. perfomance, design, fuel consumption,...) all to be rated on a 7-point scale. Our results show a strong “bias” towards the end of the response scale (probably meaning that most of the respondents find all attributes important). Performing a PCA (and intentionally violating the assumptions) we found a 5-factor model accounting for about 60% of the variance. Those 5-factors are very meaningfull from an empirical point of vue (e;g; fuel cost, purchase cost and life-cycle costs loading strongly on the same factor with very low crossloadings). However, our response scale was far from linear. I thought it would be a good idea to assess the linearity of the measures by means of the rating scale model. The data showed indeed the need to collapse categories and after a few combinations I found that a 3-point scale would do the job very well. After recoding the data, I redid a PCA. Again, I found comparable factors explaining 56% of the variance. The 5 factors now make even more sense and the loadings are very satisfactory. I was just wondering if the procedure I proposed is a sensible one, or is my rationale hopelessly flawed?
REPLY: This sounds like a situation in which your respondents are being asked to discriminate more levels (7) of importance than they have inside them (3). It probably makes sense to offer them 7 levels, so they think carefully about their choice. But the analysis of 3 levels probably matches their mental perception better.
This is a common situation when persons are asked to rate on long rating scales. For instance, "on a scale from 1 to 10 ....". Few people can imagine 10 qualitatively different levels of something. Similarly for 0-100 visual-analog scales. Collapsing (combining) categories during the analysis nearly always makes the picture clearer. It reduces the noise due to the arbitrary choice by the respondent between categories which have the same substantive meaning to that respondent.
QUESTION: I was more concerned about the fact that you use -please correct me if I’m wrong- a model (rating scale model) that assumes 1 continuous underlying factor to adapt you response scale, while afterwards you perform an analysis searching for more dimensionality in the data.
I believe it is conceivable that the use of the response scale can be dependent on the dimension one is investigating... But I also remember having read somewhere that multidimensionality can be validated by performing a FA on standardized Rasch-residuals, so I’ll pursue that way!
REPLY: Yes, this is also the manner in which physical science proceeds. They propose a theory, such as the "top quark", and then try to make the data confirm it. If the data cooperate (as it did with the "top quark") then the theory is confirmed. If the data cannot be made to cooperate (as with Lysenkoism), then the theory is rejected. In Rasch methodology, we try to make the data confirm that the variable is unidimensional. If the data do not cooperate (using, for instance, analysis of the residuals from a Rasch analysis), then the variable is demonstrated to be multidimensional. We then try to identify unidimensional pieces of the data, and we also investigate whether the multidimensionality is large enough to bias our findings.
QUESTION: Lately, I have been reading on the multidimensionality issue in the Winsteps forum, in the Winsteps help files and in Bond&Fox. Also, your previous emails have helped a great deal.
Still, I seem to struggle a little bit with the interpretation of some of the data.
As it was not my primary concern of constructing a unidimensional instrument to measure importance of car attributes in a purchase decision, I am not surprised that my data do not support the Rasch model.
My main concern is, can I use contrast-loadings of items as a basis for constructing latent factors for a confirmatory factor-analysis?
But, maybe I should display some results to illustrate up my question.
First I did recode the 7-point response scale into a 3-point scale with satisfactory scale diagnostics. Second, I take from horizontal arrangement the pathway analysis that the item difficulties are somewhat similar but that the majority of the items do not fit an unidimensional measure. This is not necessarily bad for me...
This is also confirmed with the following table I guess:
--------------------------------------------------------------------------------------------------------
|ENTRY TOTAL MODEL| INFIT | OUTFIT |PT-MEASURE |EXACT MATCH| |
|NUMBER SCORE COUNT MEASURE S.E. |MNSQ ZSTD|MNSQ ZSTD|CORR. EXP.| OBS% EXP%| Item |
|------------------------------------+----------+----------+-----------+-----------+-------------------|
| 1 2229 939 37.34 .59|1.39 8.5|1.54 9.9| .27 .45| 53.8 60.5| Purchase price |
| 7 1279 935 69.32 .69|1.35 6.7|1.43 6.2| .39 .47| 68.2 70.9| Origin |
| 3 1779 935 51.36 .56|1.16 3.8|1.20 4.5| .40 .50| 54.3 58.9| Design |
| 9 1654 932 55.16 .57|1.17 3.9|1.16 3.8| .43 .50| 53.4 58.3| Ecological aspects|
| 8 1366 937 65.75 .64|1.17 3.7|1.16 2.9| .43 .49| 63.9 66.0| Brand image |
| 16 1863 934 48.70 .56|1.09 2.2|1.11 2.5| .47 .50| 56.8 59.2| Type |
| 2 2323 936 33.75 .61| .79 -5.4| .85 -3.1| .49 .43| 69.6 62.6| Reliability |
| 15 2185 931 38.21 .58| .97 -.7| .95 -1.1| .50 .46| 60.8 59.9| Fuel costs |
| 12 1589 934 57.47 .58|1.04 .9|1.03 .7| .51 .50| 59.6 58.9| Performance |
| 5 1532 936 59.50 .59|1.17 3.9|1.18 4.0| .52 .50| 56.2 59.8| Dealer |
| 10 1922 935 46.95 .56| .82 -4.6| .84 -4.1| .52 .49| 68.1 59.4| Maintenance costs |
| 17 1789 935 51.09 .56| .88 -3.1| .88 -3.0| .54 .50| 62.9 59.0| Size |
| 14 2258 936 36.09 .59| .84 -4.1| .80 -4.4| .55 .45| 65.0 60.4| Safety |
| 13 1937 936 46.55 .56| .86 -3.6| .85 -3.7| .55 .49| 63.8 59.5| Space |
| 11 1666 935 54.98 .57| .77 -6.1| .77 -6.0| .56 .50| 69.4 58.4| Options |
| 4 1914 937 47.32 .56| .71 -7.9| .71 -7.6| .57 .49| 69.9 59.4| Ergonomy |
| 6 1812 937 50.47 .56| .96 -1.1| .94 -1.4| .58 .50| 60.1 59.1| Warranty |
|------------------------------------+----------+----------+-----------+-----------+-------------------|
| MEAN 1829.2 935.3 50.00 .58|1.01 -.2|1.02 .0| | 62.1 60.6| |
| S.D. 293.8 1.8 9.73 .03| .20 4.7| .23 4.6| | 5.6 3.1| |
--------------------------------------------------------------------------------------------------------
I am not really inclined to delete items from the list as they all seem to misfit the Rasch model (except for warranty and fuel costs). Which, again, in my case is not necessarily bad.
However, deleting items based on infit/outfit MNSQ only (ignoring ZSTD) could serve my purpose later on, but I am wondering if it is allowed to proceed this way?
Despite not being a proof of multidimensionality in the measure, it could on the other hand be an indication of multidimensionality in the data, or am I mistaken?
Third, from the following dimensionality map I presume that what I expected (multidimensionality) is (partially) confirmed:
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
-- Empirical -- Modeled
Total raw variance in observations = 27.7 100.0% 100.0%
Raw variance explained by measures = 10.7 38.6% 38.5%
Raw variance explained by persons = 5.3 19.1% 19.1%
Raw Variance explained by items = 5.4 19.5% 19.4%
Raw unexplained variance (total) = 17.0 61.4% 100.0% 61.5%
Unexplned variance in 1st contrast = 2.7 9.9% 16.1%
Unexplned variance in 2nd contrast = 1.7 6.3% 10.2%
Unexplned variance in 3rd contrast = 1.4 5.1% 8.3%
Unexplned variance in 4th contrast = 1.4 4.9% 8.0%
Unexplned variance in 5th contrast = 1.2 4.2% 6.9%
---------------------------------------------------------------
|CON- | | INFIT OUTFIT| ENTRY |
| TRAST|LOADING|MEASURE MNSQ MNSQ |NUMBER Item |
|------+-------+-------------------+--------------------------|
| 1 | .64 | 51.36 1.16 1.20 |A 3 Design |
| 1 | .56 | 65.75 1.17 1.16 |B 8 Brand image |
| 1 | .51 | 57.47 1.04 1.03 |C 12 Performance |
| 1 | .40 | 69.32 1.35 1.43 |D 7 Origin |
| 1 | .32 | 48.70 1.09 1.11 |E 16 Type |
| 1 | .27 | 47.32 .71 .71 |F 4 Ergonomy |
| 1 | .13 | 54.98 .77 .77 |G 11 Options |
| 1 | .08 | 51.09 .88 .88 |H 17 Size |
| 1 | .04 | 59.50 1.17 1.18 |I 5 Dealer |
| |-------+-------------------+--------------------------|
| 1 | -.63 | 38.21 .97 .95 |a 15 Fuel costs |
| 1 | -.60 | 46.95 .82 .84 |b 10 Maintenance costs |
| 1 | -.51 | 55.16 1.17 1.16 |c 9 Ecological aspects |
| 1 | -.37 | 36.09 .84 .80 |d 14 Safety |
| 1 | -.37 | 37.34 1.39 1.54 |e 1 Purchase price |
| 1 | -.23 | 33.75 .79 .85 |f 2 Reliability |
| 1 | -.16 | 50.47 .96 .94 |g 6 Warranty |
| 1 | -.16 | 46.55 .86 .85 |h 13 Space |
---------------------------------------------------------------
---------------------------------------------------------------
|CON- | | INFIT OUTFIT| ENTRY |
| TRAST|LOADING|MEASURE MNSQ MNSQ |NUMBER Item |
|------+-------+-------------------+--------------------------|
| 2 | .75 | 51.09 .88 .88 |H 17 Size |
| 2 | .59 | 48.70 1.09 1.11 |E 16 Type |
| 2 | .55 | 46.55 .86 .85 |h 13 Space |
| 2 | .13 | 37.34 1.39 1.54 |e 1 Purchase price |
| 2 | .02 | 38.21 .97 .95 |a 15 Fuel costs |
| |-------+-------------------+--------------------------|
| 2 | -.41 | 50.47 .96 .94 |g 6 Warranty |
| 2 | -.37 | 59.50 1.17 1.18 |I 5 Dealer |
| 2 | -.23 | 69.32 1.35 1.43 |D 7 Origin |
| 2 | -.21 | 65.75 1.17 1.16 |B 8 Brand image |
| 2 | -.19 | 33.75 .79 .85 |f 2 Reliability |
| 2 | -.14 | 51.36 1.16 1.20 |A 3 Design |
| 2 | -.14 | 36.09 .84 .80 |d 14 Safety |
| 2 | -.12 | 46.95 .82 .84 |b 10 Maintenance costs |
| 2 | -.07 | 47.32 .71 .71 |F 4 Ergonomy |
| 2 | -.07 | 55.16 1.17 1.16 |c 9 Ecological aspects |
| 2 | -.06 | 54.98 .77 .77 |G 11 Options |
| 2 | -.06 | 57.47 1.04 1.03 |C 12 Performance |
---------------------------------------------------------------
From these data I could be inclined to recognize three plausible dimensions in the measure. The + items in the first contrast describe something like “driver experience or status aspects”, the - items something like “life cycle costs”. In the second contrast the + items describe something like “practical aspects”, while the - items describe something related to the “dealer”.
Based on the remaining items the Rasch dimension, one could tentatively describe this as a “decency-luxury dimension”, (going from safety/reliability to option list/ergonomy/comfort)
The second dimension could be a “budget dimension” where people which are concerned with their budget find fuel and maintenance costs important, while on the other hand endorsers of perfomance and design items are less concerned about budget issues.
A third dimension could be something of a “supplier or car-specific dimension”. People concerned with practical specs of their vehicle could be less concerned about where it actually comes from.
I tried to incorporate those dimensions into a SEM (CFA in LISREL). Not surprisingly I had a bad fit of the data (when the model actually converged...). Especially combining the contrast-items of the first contrast proved to be a bad idea.
I believe this was because of my initial misunderstanding of FA trying to find multidimensionality in the data (even when the scores are “linearized”) whereas RaschFA seeks to explain departures from unidimensionality in the measure.
However, when using the contrasting items to construct latent factors, I have a very good fit of the data to the hypothesized model. (See graph below). Coincidence? I guess not, but this made me wonder what the nature of the relationship between CFA and RFA actually is....
So again, from a practical point of view I am curious if analyzing contrast-loadings of items can be used as a basis for constructing latent factors for a confirmatory factor-analysis? Also, it seems that omitting items with infit/outfit MNSQ > 1.4 (regardless of the ZSTD) serves the CFA a great deal in terms of fit. Do you have any idea why that is, because I expected it to be related to the testing of an unidimensional construct.
REPLY: You wrote: As it was not my primary concern of constructing a unidimensional instrument to measure importance of car attributes in a purchase decision, I am not surprised that my data do not support the Rasch model.
Reply: Do not despair! Perhaps your data do accord with the Rasch model for the most part. Let us see ...
Comment: Carefully constructed and administered surveys, intended to probe one main idea, nearly always accord with the Rasch model. If they don't, then that tells us our "one main idea" is not "one main idea", but more like a grab bag of different ideas, similar to a game of Trivial Pursuit.
You wrote: My main concern is, can I use contrast-loadings of items as a basis for constructing latent factors for a confirmatory factor-analysis?
Reply: Yes.
You wrote: First I did recode the 7-point response scale into a 3-point scale with satisfactory scale diagnostics:
Reply: Take another look at your 7-point scale. I suspect your sample can discriminate 5 levels. But with your large sample size, any loss of statistical information going from 5 categories to 3 categories probably doesn't matter.
You wrote: Second, I take from horizontal arrangement the pathway analysis that the item difficulties are somewhat similar but that the majority of the items do not fit an unidimensional measure. This is not necessarily bad for me...
Reply: That plot may be misleading to the eye. Perhaps it has squashed the y-axis and stretched the x-axis. Edward Tufte and Howard Wainer have published intriguing papers on the topic of how plotting interacts with inference.
You wrote: This is also confirmed with the following table I guess:
Reply: Yes the plot is constructed from the table. But notice your sample sizes are around 2,000. These sample sizes are over-powering the "ZSTD" t-test. See the plot at https://www.winsteps.com/winman/index.htm?diagnosingmisfit.htm - meaningful sample sizes for significance tests are 30 to 300.
So ignore the ZSTD (t-test) values in this analysis, and look at the MNSQ values (chi-squares divided by their d.f.). Only one MNSQ value (1.54) is high enough to be doubtful. And even that does not degrade the usefulness of the Rasch measures (degradation occurs with MNSQ > 2.0).
Overall your data fit the Rasch model well.
--------------------------------------------------------------------------------------------------------
|ENTRY TOTAL MODEL| INFIT | OUTFIT |PT-MEASURE |EXACT MATCH| |
|NUMBER SCORE COUNT MEASURE S.E. |MNSQ ZSTD|MNSQ ZSTD|CORR. EXP.| OBS% EXP%| Item |
|------------------------------------+----------+----------+-----------+-----------+-------------------|
| 1 2229 939 37.34 .59|1.39 8.5|1.54 9.9| .27 .45| 53.8 60.5| Purchase price |
You wrote: I am not really inclined to delete items from the list as they all seem to misfit the Rasch model (except for warranty and fuel costs). Which, again, in my case is not necessarily bad.
Reply: Please distinguish between underfit (noise) and overfit (excessive predictability). Anything with a negative ZSTD or mean-square less than 1.0 is overfitting (too predictable) in the statistical sense, but is not leading to incorrect measures or incorrect inferences in the substantive sense.
You wrote: However, deleting items based on infit/outfit MNSQ only (ignoring ZSTD) could serve my purpose later on, but I am wondering if it is allowed to proceed this way?
Reply: Rasch measurement is a tool (like an electric drill). You can use it when it is useful, and how it is useful. That is your choice.
You wrote: Despite not being a proof of multidimensionality in the measure, it could on the other hand be an indication of multidimensionality in the data, or am I mistaken? Third, from the following dimensionality map I presume that what I expected (multidimensionality) is (partially) confirmed:
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
-- Empirical -- Modeled
Total raw variance in observations = 27.7 100.0% 100.0%
Raw variance explained by measures = 10.7 38.6% 38.5%
Raw variance explained by persons = 5.3 19.1% 19.1%
Raw Variance explained by items = 5.4 19.5% 19.4%
Raw unexplained variance (total) = 17.0 61.4% 100.0% 61.5%
Unexplned variance in 1st contrast = 2.7 9.9% 16.1%
Reply: Yes, there is noticeable multi-dimensionality. The variance explained by the first contrast (9.9%) is about half that explained by the item difficulty range (19.5%). The first contrast also has the strength of the unmodeled variance in about 3 items (eigenvalue 2.7). This is more than the Rasch-predicted chance-value which is usually between 1.5 and 2.0.
This Table tells us the contrast is between items like Design ("Sales appeal") and items like Fuel Cost ("Practicality"). This makes sense to us as car buyers
---------------------------------------------------------------
|CON- | | INFIT OUTFIT| ENTRY |
| TRAST|LOADING|MEASURE MNSQ MNSQ |NUMBER Item |
|------+-------+-------------------+--------------------------|
| 1 | .64 | 51.36 1.16 1.20 |A 3 Design |
| 1 | .56 | 65.75 1.17 1.16 |B 8 Brand image |
| 1 | .51 | 57.47 1.04 1.03 |C 12 Performance |
| |-------+-------------------+--------------------------|
| 1 | -.63 | 38.21 .97 .95 |a 15 Fuel costs |
| 1 | -.60 | 46.95 .82 .84 |b 10 Maintenance costs |
| 1 | -.51 | 55.16 1.17 1.16 |c 9 Ecological aspects |
You wrote: From these data I could be inclined to recognize three plausible dimensions in the measure. The + items in the first contrast describe something like “driver experience or status aspects”, the - items something like “life cycle costs”. In the second contrast the + items describe something like “practical aspects”, while the - items describe something related to the “dealer”.
Reply: Yes, but there is also the bigger overall Rasch dimension of "buyability". The contrasts are lesser variations in the data.
You wrote: I tried to incorporate those dimensions into a SEM (CFA in LISREL). Not surprisingly I had a bad fit of the data (when the model actually converged...). Especially combining the contrast-items of the first contrast proved to be a bad idea.
Reply: Rasch and SEM are different perspectives on the data. Rasch is looking for more-and-less amounts (with predicted randomness in the data). SEM is looking for more-and-less correlations (and trying to explain away randomness in the data). So, sometimes the methodologies concur, and sometimes they disagree.
QUESTION: 1) You wrote: “Rasch and SEM are different perspectives on the data. Rasch is looking for more-and-less amounts (with predicted randomness in the data).
SEM is looking for more-and-less correlations (and trying to explain away randomness in the data).”
I am not quite sure what you mean by “amounts”. If I understand correcly this refers to “locations” on a latent Rasch dimension, is it?
So, bridging both CFA and RaschFA, a Rasch dimension may host different “factors” in the ‘traditional’ sense of the term. This makes sense, seeing that instruments like the SCL90 is alleged to have a 9-factor structure while the Rasch analysis uncovers only two dimensions.
Incase of the car survey, items with positive loadings on the 1st contrast (design, brand image, performance) may constitute a latent factor (“driving experience/status”)
and the items with negative loadings (fuel costs, environmental aspects, maintenance costs) another latent factor (“life-cycle costs”). The fact that items cluster is probably because of similar substantive meaning to the respondents, translated in high intercorrelations in the data.
In a Rasch sense, these two factors operate on different (opposing) locations of a secondary Rasch dimension. In the CFA these dynamics seem to be translated in near zero-correlations.
2) You wrote: “Take another look at your 7-point scale. I suspect your sample can discriminate 5 levels”.
Actually I did that before. I went from 7 to 6 to 5 to 4 to 3. Because the nature of the question asked “How important is this car attribute when you purchase a car”, a lot of people scored only in the top 2-3 categories. I had to collapse the original categories 1,2,3 and 4 into ‘1’; 5 and6 into ‘2’ and 7 became ‘3’ in order for each category to represent a distinct categrory of the latent variable.
3) You wrote: “That plot may be misleading to the eye. Perhaps it has squashed the y-axis and stretched the x-axis.” And “These sample sizes are over-powering the "ZSTD" t-test.”
I guess the problem I had with the bubble chart is indeed because of these inflated t-statistics because of the large sample. I should probably dispose of using this chart in my report.
About the sample size sensitivity of the ZSTD t-test in polytomous items, a recent open access paper has been published about this issue. Maybe it could be useful to include this in the manual as well... http://www.biomedcentral.com/content/pdf/1471-2288-8-33.pdf
I was thinking maybe it could be useful to inlcude effect sizes next to the t-test values, so that the guidelines could remain free of sample size issues...
REPLY: This becomes complicated for the Rasch model.
The Rasch model predicts values for SS1 (explained variance) and SS2 (unexplained variance). Empirical SS1 values that are too high overfit the model, and values that are too low underfit the model. The Rasch-reported INFIT statistics are also the (observed SS2 / expected SS2).
Winsteps could report the observed and expected values of SS1/(SS1+SS2). We can obtain the predicted values from the math underlying www.rasch.org/rmt/rmt221j.htm
You wrote: Does the t/sqrt(df) have a similar 0 to 1 range?
Reply: No. It is a more central t-statistic, with range -infinity to +infinity.
The correlation of the square-root (mean-square) with t/sqrt(df) is 0.98 with my simulated data.
So perhaps that is what you are looking for ...
pjiman1:
Hello Mike,
I wish to get your impression of my analysis of dimensionality across three waves.
Task - Analysis of dimensionality of implementation Rubric. Determine if the rubric is uni-dimensional and if this dimensionality remains invariant across waves.
Background - Items are for a rubric for assessing quality of implementation of prevention programs. 16 items, 4 rating categories. Rating categories have their own criteria. Criteria for rating category 1 is different from 2.
Items 1, 2 represent a readiness phase, items 3,4,5,6 represent a planning phase, items 7, 8, 9, 10 represent an implementation phase, items 11, 12, 13, 14, 15, 16 represent a sustainability phase.
Rubric administered at 3 waves
Using a Rating Scale model for the analysis
Steps for determining dimensionality
1. Empirical variance explained is equivalent to Modeled Variance
2. person measure var > item difficulty variance, person measure SD > Item difficult S.D.
3. Unexplained variance 1st contrast, the eigenvalue is not greater than 2.0 (indication of how many items there might be).
4. Variance explained by 1st contrast < variance of item difficulties
5. 1st constrast variance < simulated RASCH data 1st contrast variance, 1% difference between the simulated and actual data is okay, 10% is a red flag.
6. Variance in items is at least 4 times more than the variance in the 1st contrast
7. Variance of the measures is greater than 60%
8. Unexplained variance in the 1st contrast eigenvalue < 3.0, < 1.5 is excellent, and < 5% is excellent
9. Dimensionality plot - look at the items from top to bottom, any difference?
10. cross-plot the person measures
11. Invariance of the scale over time -
a) Stack , items x 3 waves of persons, perform DIF analysis of items vs. wave. We are interested in the stability of the item difficulties (measures) across time. Want to see who (persons) have changed over time as the item difficulties remain stable over time. Use a cross-plot of the persons measures wave 1 by wave 2.
b) Rack - No need to Rack given the current version of Winsteps. Racking the data see what has changed. Analysis might be appropriate here because over time, interventions occurred that impact specific items of the scale. Identify the impact of the activity by racking the items 3 waves of items by persons and seeing the change in item difficulty as an effect of treatment.
Plan - examine steps 1-10 for the measure at each wave. Look at rack and stack across all waves.
results in attached document.
My conclusion is that I have multi-dimensionality. Would you concur? Sorry for the long document.
Pjiman1
MikeLinacre:
Thank you for your post, Pjiman1.
Your list of 10 steps are indicators of multidimensionality, much as a medical doctor might use 10 steps to identify if you have a disease. At end, the doctor will say "No!" or "The disease is ....".
It is this last conclusion that is missing. What is the multidimensionality?
Based on your 23.2, and the item difficulty and misfit statistics, there is a difference between STEPS1-5 and the other items. Is this another dimension or something else?
Your scatterplot on page 34 is instructive. It measures each person on STEPS1-5 (S.E. 1 logit) and on the other items (S.E. .5 logits). So we can conceptualize the confidence intervals on your plot: the 95% confidence band extends about 1.6 logits perpendicularly away from the trend line.
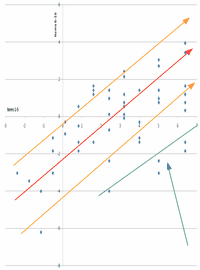
In the plot, my guess at the trendline is the red line. The confidence bands are indicated by the orange lines. The plot is more scattered than the Rasch model predicts, but is it two dimensions? The persons for which the two dimensions would be different are indicated by the green arrow. Those people have much higher measures on the first five items than on the other items. Is this a learning or familiarity effect? Is it a difference in the item dimension or a different style among the persons?
We can think of the same situation on a language test. The green area would be "second-language learners". They are much better at reading than at speaking, compared to the native-language learners of the same overall ability.
Based on this plot, for most purposes this instrument is unidimensional. But if we are concerned about the off-dimensional people, then it is two-dimensional.
Does this make sense, Pjiman1 ?
pjiman1:
Mike,
Your assistance is much appreciated. I am still reviewing your response and my response and I hope to post something soon. Just wanted to thank you for reviewing that large document.
Pjiman1
pjiman1:
Thank you very much for your insights Mike. And as always, like the previous RASCH poster Marta said, every answer leads to more questions...
Your question “what is the dimensionality” is a good one. I suspect that because dimensionality is in some ways, a social construction and based upon the needs of the measurement, the more we can connect the RASCH results with theory, the better we can justify the dimensionality of the scale.
The scale is a school wide prevention program implementation scale. Here are the items:
1. Principal commits to schoolwide SEL
2. Engage stakeholders and form steering committee
3. Develop and articulate shared vision
4. Conduct needs and resources assessment
5. Develop action plan
6. Select Evidence based program
7. Conduct initial staff development
8. Launch SEL instruction in classrooms
9. Expand instruction and integrate SEL schoolwide
10. Revisit activities and adjust for improvement
11. Provide ongoing professional Development
12. Evaluate practices and outcomes for improvement
13. Develop infrastructure to support SEL
14. Integrate SEL framework schoolwide
15. Nurture partnerships with families and communities
16. Communicate with Stakeholders
Items 1 through 10 are supposed to be conducted in sequence. Items 11 through 16 are items that are to be addressed after 1 through 10 are completed.
To me when I review the item content, Steps 1-5 constitute a “planning” dimension. Steps 6 - 10 and 11 through 16 constitute an “action” dimension. These two dimensions fit the theory of prevention program implementation and also theories of learning and adopting new innovations. Usually, when schools adopt new programs, they tend to engage in planning to adopt the new program, but they also try it out and see how it works and from that experience, make adjustments to the program. So there usually is a planning and action phase that takes place at the same time within the school as it adopts a program. The combination of engaging in both phases helps inform the school on how best to adopt the program. The dimensionality could look like this:
(2 program implementation dimensions)
<------------------------------------------------------------------------------------------>
Easy Planning tasks Hard planning tasks
<------------------------------------------------------------------------------------------>
Easy Action tasks Hard Action Tasks
However, based on the scatterplot on page 34 (and thank you for your comment on that plot) you stated - “Based on this plot, for most purposes this instrument is unidimensional. But if we are concerned about the off-dimensional people, then it is two-dimensional.” The 5 persons who scored outside the green line had high person measures on steps 1-5 and very low scores on the remaining items. So it would seem that these 5 persons saw steps 1-5 very differently than steps 6 -10 and items 11-16. Upon examination of the persons that produced these scores, not sure if there are learning or familiarity effects here and not sure if a different style is evident (schools that attend to steps 1-5 more so than other schools). I am sensing that you are wondering if the 2nd dimension of this instrument means anything to those 5 persons who are outside of the 95% confidence band. Based on what I know of those persons, I cannot think of anything that would distinguish those 5 persons on this second dimension. I have no reason to think that the 2nd dimension helps me discriminate between the persons. It could be that those 5 persons (schools) had low scores on the 2nd dimension. In other words, I am not concerned about those 5 persons that are off dimension.
You also said that based on the PCA 23.2 tables, item difficulties and misfit statistics that items 1-5 are a 2nd dimension. So for the most part, there are two dimensions here, but if the persons do not produce scores that suggest that they are using the two dimensions of the scale in notably different ways, then we can say that the scale is uni-dimensional?
Let’s say the two dimensions are planning and action dimensions. If the planning dimension is easiest to do and the action dimension is harder to do, then perhaps this is a one dimensional scale with planning on the easy end and action on the harder end. Like this:
(program implementation dimension)
<----------------------------------------------------------------------------------------->
Planning tasks (Easy) Action tasks (Hard)
I am leaning towards the one dimensional scale for simplicity sake. I can say that there are two dimensions here, but in some ways (based on the scatterplots), the two dimensions do not give me much more information than if I had just a one dimensional scale. So to answer your question - “what is the multi-dimensionality?” I would say that there is a planning and an action dimension, but all the information I need is best served when the two dimensions are together on the same scale.
If this conclusion satisfies your question “What is the multidimensionality?” then I believe my work in establishing the two dimensions of the scale, but treating them as if they are one scale, is done, correct?
Additional questions:
Thank you for your comment on the scatterplot on page 34. You made a guess at the trend line, how did you arrive at that guess? Were the scatterplots for wave 1 (p.9) and wave 2 (p.22) not as instructive or did they not show signs of multi-dimensionality, that is they did not have enough persons that were outside the 95% confidence band.
You mentioned that based on the item difficulties and the misfit statistics, you saw another dimension. What did you see in those stats that helped you come to this conclusion?
Based on the results, do you think there might be additional dimensions within steps 6 -10 and steps 11-16?
Were the rack and stack plots (p. 36 - 39) helpful in any way? Did the Stack plot, with its items locating at beyond the +-2 band at different waves suggest something about the non-invariance of the items across waves? Does it say something about the dimensionality of the measure? Did the Rack plots say something about which items changed from wave to wave? Does it say something about the dimensionality of the measure?
Thanks again for your valuable work and assistance. The message board is a great way to learn about RASCH.
pjiman1
pjiman1:
Hi Mike,
Got a message that you had replied to my latest post on this thread, but when I logged on, I could not find it. Just wanted to let you know in case the reply did not go through properly. Thanks!
pjiman1
MikeLinacre:
Pjiman1, I started to respond, and then realized that you understand your project much better than I do. You are now the expert!
pjiman1:
Thanks Mike for the affirmation. It's nice to know I can proceed.
pjiman1
mathoman:
thank you all
we are folow up your posts
dr.basimaust:
Dear sir, would you answer my question concerning best method to determin unidimenstionality of an five category attitude scale composing 30 items distrubuting on three subscales, each has 10 items. the scale has been applied on 183 students. thank you dr. Basim Al-Samarrai
MikeLinacre:
Thank you for your post, Dr. Basim Al-Samarrai.
In the Winsteps software, Table 23 "dimensionality" is helpful.
https://www.winsteps.com/winman/index.htm?multidimensionality.htm in Winsteps Help suggests a procedure to follow.
sailbot:
I wish this post could be kept at the top. It does seem that many of us have dimensionality questions, and this is probably the best thread on the issue. I found it 1000 time helpful.
rag:
I have found this thread super helpful, thank you Michael and everyone else.
I follow the key differences between the CFA and Rasch PCA methods to assess dimensionality, and why they may converge in some cases and not in others. My question relates to how we identify what is going on when the results diverge dramatically.
I have an assessment that contains 9 dichotomous items with 417 respondents, which hypothetically reflect a single latent construct or dimension. Running it through a Rasch model, and looking at the PCA of the residuals, the first contrast/eigenvalue is 1.4. See results:
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
-- Empirical -- Modeled
Total raw variance in observations = 12.5 100.0% 100.0%
Raw variance explained by measures = 3.5 28.0% 27.7%
Raw variance explained by persons = 1.8 14.0% 13.9%
Raw Variance explained by items = 1.7 14.0% 13.8%
Raw unexplained variance (total) = 9.0 72.0% 100.0% 72.3%
Unexplned variance in 1st contrast = 1.4 11.4% 15.8%
Unexplned variance in 2nd contrast = 1.3 10.5% 14.5%
Unexplned variance in 3rd contrast = 1.2 10.0% 13.9%
Unexplned variance in 4th contrast = 1.1 9.0% 12.5%
Unexplned variance in 5th contrast = 1.0 8.4% 11.6%
This tells me that I've got evidence for a single dimension.
However, when I run through a CFA, the story is very different. I am using the lavaan package in R, which deals with dichotomous items by calculating tetrachoric correlations and then running some form of a weighted least squares algorithm. A single factor model gives me poor fit (RMSEA=0.063, Comparative Fit Index=0.714). The loadings are all over the place, some positive and some very negative. A 2 factor model fits somewhat better, but still has problems.
I should also point out that while KR20 is around 0.6, person-separation reliability is .04, so my data are not the greatest (looking at the item/person map, most items are way below most respondents scores, with 8 of 9 items having a pvalue over 0.80).
From a Rasch perspective, I have evidence for unidimensionality, from a CFA perspective I most certainly do not. My thought is initially that the measures explain a small portion of respondent variance (28%), the remaining variance may not be systematically dependent in any other way, so the PCA of Rasch residuals wouldn't find a high contrast. The CFA, running against the full item variance (rather than what is leftover after the measure variance is removed) just picks up a lot of that noise that isn't related to anything else. If I am right about this, then it looks like I have evidence that the assessment isn't really measuring anything systematic and should probably be given a serious examination from the conceptual perspective before moving forward.
Any thoughts?
Mike.Linacre:
rag, have you looked at https://www.rasch.org/rmt/rmt81p.htm ? It indicates that one Rasch dimension = two CFA factors.
177. Ability strata
Raschmad January 1st, 2008, 5:45pm:
Hello folks,
Separation is the number of ability strata in a data set.
For example, a person separation index of 4 indicates that the test can identify 4 ability groups in the sample.
I was just wondering if there's a way to distinguish these 4 ability groups. Is there a way to (empirically) conclude that, for instance, persons with measures from say, -3 to -1.5 are in stratum 1, persons with measure between -1.5 and 0.5 are in stratum 2 and so on?
Cheers
MikeLinacre:
Thank you for your question Raschmad.
You write: "Separation is the number of ability strata in a data set."
Almost "Separation is the number of statistically different abilities in a normal distribution with the same mean and standard deviation as the sample of measures estimated from your data set." - so it is a mixture of empirical and theoretical properties, in exactly the same way as "Reliability" is.
You can see pictures of how this works at www.rasch.org/rmt/rmt94n.htm.
Empirically, one ability level blends into the next level, but dividing the range of the measures by the separation indicates the levels.
drmattbarney:
[quote=MikeLinacre]Thank you for your question Raschmad.
dividing the range of the measures by the separation indicates the levels.
Great question Raschmad; and excellent clarification Mike. The pictures were terrific. This seems very helpful for setting cut scores, whether passing a class, or pre-employment testing. Naturally, depends on the theory and applied problem one is addressing with Rasch measures, but am I on the right track?
Matt
MikeLinacre:
Sounds good, Drmattbarney. You would probably also want to look at www.rasch.org/rmt/rmt73e.htm
Raschmad:
Mike and Matt,
I had standard setting in mind when I posted the question.
However, I am not sure to what extent this can help.
Probably some qualitative studies are required to establishthe the validity of the procedure (Range/Separation).
Cheeers
jimsick:
Mike,
I'm reviewing a paper that reports a Rasch scale with a person reliability of .42 and a separation of .86. I'm just pondering what it means to have a separation of less than 1. From the Winsteps manual:
SEPARATION is the ratio of the PERSON (or ITEM) ADJ.S.D., the "true" standard deviation, to RMSE, the error standard deviation. It provides a ratio measure of separation in RMSE units, which is easier to interpret than the reliability correlation. This is analogous to the Fisher Discriminant Ratio. SEPARATION2 is the signal-to-noise ratio, the ratio of "true" variance to error variance.
If the ratio of the true variance to error variance is less than one, does that imply that the error variance is greater than the total variance (not logically possible)?
Or does "true variance" = true score plus error variance? Clearly, it is an inadequate scale, but does separation below one indicate that NO decisions can be reliably made?
regards,
Tokyo Jim
MikeLinacre:
Tokyo Jim: the fundamental relationship is:
Observed variance = True variance (what we want) + Error variance (what we don't want).
When the relability <0.5 and the separation <1.0, then the error variance is bigger than the true variance. So, if two people have different measures, the difference is more likely to due to measurement error than to "true" differences in ability.
In real life, we often encounter situations like this, but we ignore the measurement error. The winner is the winner. But the real difference in ability has been overwhelmed by the accidents of the measurement situation.
The 2009 year-end tennis tournament in London is a good example. The world #2, #3 and #4 players have all been eliminated from the last 4. Are their "true" abilities all less than the world #5, #7 and #9? Surely not. But the differences in ability have been overwhelmed by accidents of the local situation, i.e., measurement error.
C411i3:
Hi I am having some trouble interpreting my separation/strata analysis. I've got person separation values from 1.03 to 1.17, person strata values from 1.71 to 1.89 , and person reliabilities from 0.52 to 0.58 (depending on if extreme measures are included).
These values lead me to think that my test cannot differentiate more than 1 group, perhaps 2 at best. However, previous research has shown that this test (sustained attention task) can detect significant differences in performance in clinical groups (e.g., ADHD kids on- and off-medication).
I am having trouble reconciling the Rasch result (only 1 group) with what I know the test can do in application (distinguish groups).
The items on the test calibrate to a very small range of difficulties (10 items), which is why this result is produced. Is there another way to look at group classification that I am overlooking? Do these statistics mean this test can't really distinguish groups? Counter to other evidence
Any and all advice is appreciated!
-Callie
Mike.Linacre:
Thank you for your question, Callie.
Reliability and separation statistics are for differentiating between individuals. With groups, the differentiation depends on the size of the group. For instance, very approximately, if we are comparing groups of 100, then the standard error of the group mean is around 1/10th of the individual amount, and so the separation for group means would be around 10 times greater than for individuals.
579. Control file
ning April 13th, 2008, 6:12pm:
Dear Mike,
If I set ISGROUP=0, it's PCM that applies to all items...what if I want to run part of the items using RSM and part of the items using PCM using one data set in one analysis? How do I set up the control file?
Thanks
MikeLinacre:
Here's how to do it Gunny. Give each group of items, that are to share the same rating scale, a code letter, e.g., "R". Each PCM item has the special code letter "0" (zero). Then
ISGROUPS = RRR0RRR000RRRRRRRRR
where each letter corresponds to one item, in entry order.
ning:
Thanks, Mike, I should of known that by now...
ning:
Dear Mike, Could you please help me out on the following control file...what am I doing wrong? I'm not able to run at all in the Winsteps.
Thanks,
ITEM1 = 1 ; column of response to first item in data record
NI = 8 ; number of items
XWIDE = 3 ; number of columns per item response
ISGROUPS =RRRRRRR0 ; R=RSM, 0=PCM,
IREFER=AAAAAAAB
IVALUEA=" 1 2 3"
IVALUEB=" 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99100"
MikeLinacre:
There is something strange about this, Gunny. There is no CODES=. Perhaps you mean:
CODES = " 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99100..."
IVALUEA=" 1 2 3"
IVALUEB=" 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99100..."
ning:
Dear Mike,
You just saved my day...I've been staring at it long enough...
Thanks.
mukki:
I'm steal have problem to develop Control fine
MikeLinacre:
Mukki, what is your problem?
dachengruoque:
oh, learned a lot from the post as well, thanks a lot, dr linacre!
783. convert raw data to rasch scaled
danielcui March 31st, 2008, 1:53am:
hi, mike,
i am a rookie in rasch. i am interested in performing confirmatory factor analysis on rasch scaled data. where do i start? i use winsteps.thanks.
MikeLinacre:
Thank you for your question, Daniel.
Do you want to do CFA with Rasch measures as one of the variables?
Or do you want to do CFA on the observations that are used to estimate Rasch measures?
Or .... ?
danielcui:
hi, mike,
thanks for your response. i am validating a questionnaire using rasch analysis. however, i found there is only 40% variance explained by measures, when run the PCA. so i guess it's not in unidemensionality, therefore, i intend to use CFA on rasch scores to conclude the dimensions. please correct me if i am wrong.
daniel
MikeLinacre:
"only 40% ... so i guess it's not unidimensional"
The good news is that "only 40%" indicates that the person and item samples may be central. It does not indicate dimensionality.
For multidimensionality, we need the 40% and the size of the next explanatory component. If it is 20%, then the data are multidimensional, but if it is 2% then they are not ....
danielcui:
hi, mike,
the next component is 7.8%, would it suggest unidimensionality?thanks.
daniel
MikeLinacre:
No test (or even physical measurement) is perfectly unidimensional, Daniel. So the crucial question is "Does this degree of multidimensionality matter?" It did in measuring heat with the earliest thermometers, but it no longer does with most modern thermometers. Then the next question is "what are we going to do about the multidimensionality?"
7.8% would certainly suggest that you should take a look at the items loading on each end of the component. What is the substantive difference between them? Is the difference important enough to merit two separate measurements (like height and weight) or is it not worth the effort (like addition and subtraction).
You could also divide the test in two halves, correspond to the "top" and "bottom" items. Perform two analyses, then cross-plot the person measures from each half. What does it tell you? Are the differences in the person measures between the two halves big enough to impact decision-making based on the test? Which half of the test is more substantively accurate for decision-making?
danielcui:
hi, mike,
i looked at the two halved and found there is some different between each other, in terms of the item dimension. then, what could i next? thanks.
MikeLinacre:
Daniel, "there is some different between each other" - so the question becomes "Does the difference matter in the context of the test?" This is a substantive question about the content of the test. Should there be two test scores or measures reported for each person, or is one enough?
danielcui:
thanks, mike, i guess it need to be separate into two measures.
danielcui:
Hi Mike,
There is IPMATRIX output file in Winsteps. When intend to apply Rasch scaled data in factor analysis, should I use expected response value or predicted item measure? thanks.
MikeLinacre:
What is the purpose of your factor analysis, Daniel?
If we use the "expected responses", then we are factor-analyzing Guttman data. Our factor analyis should discover factors related to the Rasch dimension and the item and person distributions.
If we use the predicted item measures, then we are removing the item difficulties from the raw observations, so the factor analysis will emphasize the person ability distribution. But I have never tried this myself. It would be an interesting experiment, perhaps meriting a research note in Rasch Measurement Transactions.
danielcui:
Hi Mike,
Thanks for your quick reply.
My research is about to refine a questionnaire in quality of life. My intention using Rasch is to convert the response of the questionnaire into interval data, then use factor analysis to identify domains of the construct. Thanks to your online course,I have completed item reduction and category collapse, now I need know the response pattern from the sample subjects,which is the domain of the construct, according to my subjects sample.
I reckon what I mentioned two parameters in the post might not be appropriate, I tried "predicted person measure" instead, which seemed reasonable with the results.( see in the attachment) What do you think? Thank you.
Cheers,
Daniel
MikeLinacre:
There are two factor-analytic approaches to dimensionality (factor) investigations, Daniel:
1. Exploratory common-factor analysis (CFA) of the observations. This looks for possible factors in the raw data. The expectation is that the biggest factor will be the Rasch dimension, and the other factors will be small enough to ignore.
2. Confirmatory principal-components analyis (PCA) of the residuals. The Rasch dimension has been removed from the observations leaving behind the residuals. The PCA is intended to confirm that there are no meaningful dimensions remaining in the residuals. Thus the Rasch dimension is the (only) dimension in the data.
The analysis of "predicted person measure" is closer to CFA of the observations, but with the observations adjusted for their item difficulties. An analysis of data with known dimensionality would tell you whether this approach is advantageous or not.
danielcui:
Hi Mike,
Thanks for clarify the definitions. Sometimes people use CFA as abbreviation for comfirmatory fact analysis and EFA for exploratory factor analysis.
One advantage of Rasch analysis is to convert ordinal data to interval ones. In my case, I try to use Rasch analysis convert the ordinal response "very happy", "happy", "not happy"into interval data so I can use them for linear data analysis. Does predicted person measures provide this information? It looks as give each item with a calibrated measures from each respondent.Please correct me if I am wrong. Thank you.
Daniel
MikeLinacre:
Apologies for the confusion about abbreviations, Daniel.
Rasch converts ordinal data to the interval measures they imply. We can attempt to convert the ordinal data into interval data by making some assumptions.
If we believe that the estimated item measures are definitive, then we would use the predicted person measures.
But if we belive that the estimated person measures are definitive, then we could use the predicted item measures.
This suggests that "predicted person measure - predicted item measure" may be a more linear form of the original data.
danielcui:
thank you so much, mike.
811. The mean measure for the cented facet is not 0
Jade December 28th, 2008, 5:31am:
Dear Mike,
I am doing a Facets analysis of rater performance on a speaking test. I non-centered the rater facet since it is the facet I am interested. The output, however, shows the mean measure for the Examinee facet is .16. I was expecting a 0 for the centered facets such as examinee. I did get a 0 on the item facet. Could anyone here help to explain why the mean measure is .16 not 0 for the centered facet of examinee? My model statement is like this,
Facets = 3 ;3 Facets Model: Rater x Examinee x Item
Non-center = 1
Positive = 2
Pt-biserial = Yes
inter-rater = 1
Model = #,?,?,RATING,1 ;Partial Credit Model
Rating Scale = RATING,R6,General,Ordinal
Also I am confused with the SD on the rater facet. I got SD 1.22 (for sample). In Bonk and Ockey (2003), they square the SD to get the variance value to see to what extent each facet contributes to the total variance. In my case, how do I explain the variance that raters contribute to the total variance?
Thank you.
MikeLinacre:
Thank you for your questions, Jade. Does this help?
1. Your specifications are correct. In your examinee facet, the centering of 0 applies to the non-extreme examinee measures. There are probably some extreme person measures (corresponding to minimum and maximum possible scores) which are included in the computation of the mean, but not of the centering.
2. Explained variance can be approximated by using the element S.D.
Facets Table 5:
Explained variance = Step S.D.^2 - Resid^2
Explained variance % = Explained variance * 100 / Step S.D.^2
b. From Table 7:
v1 = (measure S.D. facet 1)^2
v2 = (measure S.D. facet 2)^2
v3 = (measure S.D. facet 3)^2
vsum = v1 + v2 + v3
b. Compute Explained variance for each facet:
Explained variance % by facet 1 = (Explained variance %) * v1 /vsum
Explained variance % by facet 2 = (Explained variance %) * v2 /vsum
Explained variance % by facet 3 = (Explained variance %) * v3 /vsum
MikeLinacre:
Good, that explains everything, Jade.
1. Extreme measures are outliers in the distribution of measures, but they may be what you want. For instance, on a classroom test, teachers are delighted when someone "aces" the test.
2. Unexplained variance is 22.37%. The Rasch model predicts and requires random unexplained variance in the data. The variance explained by the items is very low (0.03%). As your Table 6 shows, your items have almost equal difficulty. Perhaps this is also intended. This does suggest that your data could be usefully modeled using two facets (Examinees and Raters). You could then use two-facet software, such as Winsteps, to do a more-detailed investigation into the dimensionality of your data.
You are modeling each rater to operationalize a personal rating scale (#). This is good for investigating rater behavior, but obscures dimensionality and "variance explained". Please model all raters to share the same rating scale. (? instead of #). This will give you a more accurate perspective on the variance explained by the raters.
MikeLinacre:
Thank you, Jade. Sorry, the documentation of "agreement" is inadequate.
What it means is "Agreement on qualitative levels relative to the lowest observed qualitative level".
So, imagine all your ratings are 4,5,6 and all my ratings are 1,2,3.
If we use the (shared) Rating Scale model. Then we will have no exact agreements.
But if we use the (individual) Partial Credit model, then we agree when you rate a 4 (your bottom observed category) and I rate a 1 (my bottom observed category). Similarly, your 5 agrees with my 2, and your 6 agrees with my 3.
Since you want "exact agreement" to mean "exact agreement of data values", then please use the Rating Scale model statistics.
Jade:
So it is the ranking. It now makes sense. Thank you very much for the clarification.
Happy New Year!
812. Seeking advice about ConQuest
Tommy December 22nd, 2008, 7:32am:
I am a research assistant of Hong Kong Institute of Education. I want to use ConQuest to run a partial credit model. However, I have found some problems. I hope someone can give me some advice to solve them. Below is part of the syntax of my program:
Data irt01.dat;
Format gender 1 paper 2 responses 3-71;
Labels << text05.lab;
codes 1,0.5,0;
recode (1,2,3,4,n,o,z) (1,0,0,0,0,0,0) !item(1);
recode (1,2,3,n,o,z) (1,0,0,0,0,0) !item(2);
recode (1,2,3,4,5,m,n,z) (0,0,0,0,1,0,0,0) !item(3);
recode (0,1,n,z) (0,1,0,0) !item(4);
recode (0,1,n,z) (0,1,0,0) !item(5);
recode (0,1,n,z) (0,1,0,0) !item(6);
recode (0,1,n,z) (0,1,0,0) !item(7);
recode (0,1,n,z) (0,1,0,0) !item(8);
recode (0,1,2) (0,0.5,1) !item(9);
recode (0,1,2) (0,0.5,1) !item(10);
......
My first question is can I recode the answers into decimal? Such as items 9 and 10, I want to give 0.5 mark only for choice 1 to indicate the students are only partially correct. However, the program cannot be executed. How can I do?
Later, I change the scoring system for these two questions like this: 2 marks represents fully correct, 1 mark represents partially correct and zero represents wrong, then I get the reuslt. Can I make this modification?
Indeed, I want to make the weighting of all items are the same. If I can recode all the items into 1,0.5 & 0 is prefect. Moreover, I have tried to increase the full marks of items 1,2,3...... into 2 marks instead of 1 mark. However, the program cannot be executed. How can I solve it?
My second question is the execution time of the program is rather long, also I spend a lot of time to write the syntax "recode" in my program because there are around 70 questions. However, only four of them are needed to be counted as 1 (fully correctly), 0.5 (partially correct) & 0(wrong). The remaining questions are simply counted as 1 (correct) & 0 (wrong). Any improvement can be made to let the program looks more precisely and the execution time is shorter?
MikeLinacre:
Tommy, a ConQuest expert will respond.
But here's a start:
ConQuest does not accept decimals. The scoring must be consecutive integers.
So not: 0-0.5-1, but 0-1-2
Suggestion: If you want 0-2, then put in a dummy record with a "1" in it, so that the data look like 0-1-2.
Or, enter the 0-1 item twice in the data.
Tommy:
Thank you very much !! :)
813. How to attach files to posts on the forum
Jade December 28th, 2008, 5:36am:
Dear Mike,
How do I attach tables or my Facets program when I post? I just couldn't find any icons for attachment.
Thanks.
Happy New Year
Jade
MikeLinacre:
Thank you for asking, Jade. The attachment feature is now activated.
Click on "More Post Options"
Then "Browse" to the file you want to attach.
814. basic stuff pls
harry December 15th, 2008, 10:48am:
hello, i need some basic assisstance in interpreting rasch analyis. My assignment is to determine unidimensionality and fit of data for depression scale with 20 items on two different group of subjects, one on children without parents and on children with parents. The results indicate that the scale works totally differently in two samples. In children without parents total explained variance is 63.2% (1 kontrast 5,2% unexplained) and for children with parents explained variance is 38.3% (1 kontrast 14,8% unexplained). Further, almost whole scale presents item misfits for children with parents (12 items misfit, outside the range 0,7-1,3). For children without parents number of misfits is 8 and the items excluded are different in two samples. Now my question is: 1. Is there something wrong with the scale because different items are excluded from the scale in 2 samples in order to represent the fit (or does it work on type of data obtained from the scale, meaning i cant mix two groups together) children without parents are significalntly more depressed) eg. can i use it on both samples?
2. Is there anything else i need to be aware of in interpreting these data?
I have to mention i analized two groups separately (each group sample is 70)
thank you!
MikeLinacre:
Thank you for your questions, Harry. This is an ambitious project.
1. The easiest way to discover whether the depression scale can be used for both samples is to:
a) analyze all the data together, but with a code in each person label (child identification) indicating which sample the child belongs to.
b) do a DIF analysis of the items by child-type. This will tell you which items had different measures for the two samples, and how much the difference is. Differences less than 0.5 logits are not differences.
2. Fit: the fit range 0.7 - 1.3 is tight for these data. That range is more suited to a multiple-choice test. https://www.rasch.org/rmt/rmt83b.htm "Reasonable mean-square fit statistics" suggests 0.5 - 1.7 for clinical-observational data, or perhaps 0.6 - 1.4 for survey data. Based on Rasch theory, 0.5 - 1.5 are productive for measurement. Values above 2.0 are destructive for measurement.
3. Contrast: it is useful to look at the eigenvalues (first column of numbers in Table 23.0). From your numbers, for children without parents Contrast 1 has an eigenvalue = 20* 5.2 / (100-63.2) = 4 items. This is large, so it suggests that you look at the plot in Table 23.2. Is there a cluster of items at the top or the bottom? These items could be a meaningful sub-dimension. In the MMPI, depression and lethargy are included in the same scale. Rasch analysis of MMPI data shows they are different variables, but the developers of the MMPI chose to keep them together. So you must decide the same thing: are the two variables different enough for two scales, or are they similar enough to be included in one scale.
Does this help, Harry?
harry:
thx a lot for the answer, but what i am not sure is how can a test such as that be differently calibrated for two groups and other thing is what is the best way of interpreting validity of the test (through eigenvalues or percentage of variance explained, which tells me that the test is valid, is there a minimum on variance explained or eigenvalue)?
I must say i am new to rasch analysis and you replies really inspire me to deepen my knowledge in this interesting field. Again, thx a lot
MikeLinacre:
These are challenging questions, Harry.
1. "How can a test such as that be differently calibrated for two groups?"
Each person sample would provide slightly different estimates of the item difficulties. We expect these differences to be roughly the size of the standard errors of the item difficulty measures. So we need to investigate whether the differences are within statistical expectations, or due to something substantive. You could cross-plot the two sets of item difficulties, or the two sets of person measures (for the same raw scores). Draw in the confidence intervals on the plots, and you will see whether the measures are invariant (statistically the same) or not.
2. "what is the best way of interpreting validity?"
There are many different types of validity. In Rasch analysis, we usually start with
a. Construct validity - does the item difficulty hierarchy agree with the hierarchy based on what we want to measure, e.g., on an arithmetic test, are "division" items shown as generally more difficult than "addition" items?
b. Predictive validity - do the person measures agree with the external evidence we have about the persons. For instance, on our arithmetic test, do upper-grade children have higher measures than lower-grade children?
c. Statistical validity - these include "reliability" (is the measure hierarchy statistically reproducible?) and 'unidimensionality" (is the instrument measuring one latent trait?).
Your concern is unidimensionality.
We could look at the amount of variance explained, but it depends on the dispersion of the person and item measureswhich has no minimum proportion - see www.rasch.org/rmt/rmt221j.htm
So a more useful approach is to look at the strength of the biggest sub-dimension in the data (identified by the 1st Contrast in the PCA of residuals). This needs to have at least 2-item-strength (eigenvalue 2) for us to seriously consider it a sub-dimension. Then we look at the substance of those items (e.g., "division" vs. "addition" on an arithmetic test) to identify whether the sub-dimension is a separate dimension (which it could be for test diagnosing learning difficulties) or whether the sub-dimension is a content strand within the dimension (which it could be for a standardized math test).
How are we doing so far?
harry:
It is going great, thank you! If i may be free to ask some additional questions:
1. in interpreting 23.2 plot, do items need to be equally distributed across the plot or should there be kind of line distribution (like regression line, so all items are more or less on the same line).
2. What if items that are clustered together do not make logical sense to be considered a separate dimension, should i just conclude that sample is not representative?
3. In almost all items differance between categories is higher then 0.5 logits. What are the possible conclusions?
And finally, i cant stress enough how your assistance has been valuable for me. Thank you so much
MikeLinacre:
Glad you are looking into the details, Harry.
1. In Table 23.2, the important distinction is the "contrast" between the top and the bottom of the plot. We expect to see a random scatter around the x-axis.
2. "clustered together do not make logical sense" - this is what we hope to see. It indicates that the plot is reporting random noise, which is what the Rasch model predicts we should see.
3. "In almost all items differance between categories is higher then 0.5 logits."
Does this mean "difference between item difficulty measures in different analyses"? If so, stratify the items by difference to see if there is any pattern to the meaning, or cross-plot the item measures with labeled points to see if they have any meaning. In one of our analyses, this revealed that "motor" and "mental" items had different profiles in different samples.
But if "categories" refers to "rating scale categories", then differences greater than 0.5 logits between adjacent rating-scale categories are desirable.
harry:
Hi again and thx again!
What i meant in 3rd question was that the difference between children with and without parents on all items was higher then 0,5 logits. Does it change anything?
And finally how do you check for the "rating scale categories difference in logits", what plot should i look at?
I really appreciate all the effort you put in answering these questions!
MikeLinacre:
You are busy, Harry!
1. One of your findings is that children with parents are more than 0.5 logits more (or less?) depressed than children without parents. This is probably a statistically significant difference (i.e., not due to chance alone). Please look at your items to see what 0.5 logits means in substantively.
2. "Rating scale categories difference in logits" -This was my guess at what you meant. But you do need to check that your rating scale is functioning as intended. This is Table 3.2 in Winsteps. Is there a noticeable advance from one category to the next? Do the responses fit in the categories?
harry:
I will never understand rasch if i dont understand it now with such a great teacher :)
Ok, my rating scale has 4 categories. In outfit/misfit they are all in the range between .87-1.14.
1. How to interpret results in structure calibration and category measure, what numbers are we expecting to see?
2. Also what is the interpretation of M-C and C-M and is it the estimate discrimination what am i supposed to look at? Estimate discrimination for the 1st category- none, 2nd- 1.34, for 3rd- 0.74 and for 4th 0.94 (interpretation?)
thank you
MikeLinacre:
Harry, if your mean-squares are in the range .87-1.14, then they are very good.
1. Rating scale categories: Please see https://www.rasch.org/rn2.htm
2. Obscure fit statistics: Winsteps, like almost all statistical software, reports many more numbers than are needed for any research project. It is likely that none of the numbers in your 2. are informative for you project. These other numbers are useful for diagnosing problems when the mean-squares are bad.
harry:
thanks a lot! No more question at this stage
815. Measuring magnification
hellogreen November 27th, 2008, 1:03am:
How to Measure magnification
How can I see how strong a magnifying glass is?
I bought this magnifying glass http://www.liangdianup.com/inventory/189901.htm and I want
to know how to test it to see how strong it is. I hear a lot of people talk about
magnifying and how strong the magnification is, but I would like to know the true
magnification of my magnifying glass. I have a few of them and some seem stronger then
others. How can I rate these? How can I pin a correct number on mine? How do the companies
that make these come up with these numbers.
MikeLinacre:
Sorry, this is outside my area of expertise. But you (or someone) has posted this question on many Forums, so perhaps one of those has a simple answer.
816. Assessing Unidimensionality with Scree Plots
mdeitchl November 20th, 2008, 3:50pm:
Hi -
I'm analyzed polytomous data using the partial credit model (ISGROUPS=0). I'm trying to assess unidimensionality but struggling to understand/interpret the output. I have multiple samples so I am, at the same time, trying to assess the comparability of the scale across different populations. My scree plot results are fairly consistent across data sets which I know is good, but I wish I could understand better what the results mean.
So far, I have been using the scree plot generated for the first contrast (component?) and assessing which item residuals showed similar correlations. Several item residuals load at 0.5 to 0.8, most of the others load at -0.7 to -0.6 and a few at -0.1 to 0.0. Does this mean there are likely 3 dimensions in my initial scale?
When I eliminate several items from my scale (e.g. those not in the 0.5-0.8 range), then the remaining items all load very near together (-0.7 to -.5) but one of the items (previously in the same range as those now loading at -0.7 to -0.5) now loads at 1.0 in all data sets. What does this mean? Given the content of the items, I have a hard time believing that the one item at 1.0 actually reflects a different dimension of my construct.
My scale consists of very few items and each items has 3 possible responses (2 steps) - could this have anything to do with it?
A related question: when assessing unidimensionality for polytomous data, does the scree plot reflect the residual for the item (by taking the average of the residuals of the items steps for that item)?
Is there anything else that should be checked when using few items in a scale to confirm that the items reflect only 1 dimension? Should I be looking at more than just the first scree plot generated from the output - and what do these additional scree plots actually mean?
Thanks in advance!!! Megan
MikeLinacre:
Thank you for your post, Megan.
You wrote: "My scale consists of very few items" - this makes any dimensionality analysis doubtful.
In Rasch theory, there is one unifying dimension, the Rasch dimension, and then as many uncorrelated sub-dimensions as there are items. This means that, in data which fit the Rasch model, we expect the first contrast to be between one or two items (which accidentally correlate) and the other items.
There is not a secondary dimension until there are at least two items which correlate strongly together, or better 3 items. These 3 or more items should share some clear substantive aspect, for instance, they should all be focused on the same aspect of behavior. These 3 items would contrast with the other (at least 3) items.
The data structure (dichotomous or polytomous, rating scale or partial credit) has only a minor influence on dimensionality.
Residuals are the difference between the observed ratings and their expectations, irrespective of the data structure. For instance, in a 3-category rating scale (1-3), the observed rating may be "2", but its model-based expectation is 1.7. So the residual is 2 - 1.7 = 0.3.
OK? Does this help, Megan?
mdeitchl:
Thanks, Mike - this gets me started - though I still have a couple of questions.
I am starting with 9 items. You write "we expect the first contrast to be between one or two items". Translating this to the Winsteps output, does this mean the "unexplained variance in the 1st contrast" should be between 1 and 2? And what if it is higher -does that mean the fit is not good?
You write "there is not a secondary dimension until there are at least two items which correlate strongly together, or better 3 items....These 3 items would contrast with the other (at least 3 items)." To assess this, do I look at the output from contrast 1? or a later contrast? If I look at contrast 1, I have 3 items that load at -0.55 to -0.62 and 3 items that load at 0.62-0.70. The substance between the two sets of items is somewhat different. Would this lead one to believe the 6 items could together reflect 2 dimensions?
If I am on the right track here, I then still need advice on what is the next step. If I retain only the set of items (in this case the 3 item loading at 0.62-0.70) representing the attribute I am interested in, do I need to assess unidimensionality again using only a 3 item scale or is unidimensionality assessed only once at the outset (using all items)? Of course, I will assess infits/outfits, etc. for the 3 item scale but I am just not clear if unidimensionality also need to be verified when a revised scale is identified.
From your message below, I think I understand that unidimensionality in way of a scree plot cannot really be assessed for a 3 item scale. Is that right? As a note: in one of my samples, the 3 item scale explains 31.5 of the 34.5 total variance in the observations. It is more modest in the other data sets but still acceptable - I think - at around 70-75%.
Thanks for your help!
Megan
MikeLinacre:
Thank you for your questions, Megan.
1. "does this mean the "unexplained variance in the 1st contrast" should be between 1 and 2?"
Reply: Yes, that is what simulation studes indicate, e.g., https://www.rasch.org/rmt/rmt191h.htm
2. "Would this lead one to believe the [9] items could together reflect 2 dimensions?"
Reply: Yes, but your test is already short.
3. "unidimensionality in way of a scree plot cannot really be assessed for a 3 item scale"
Reply: Yes. Each item is modeled to share the Rasch dimension, but otherwise to manifest its own dimension, ("the items are to be as similar as possible on the Rasch dimension, but as different as possible on all other dimensions"). But there are always some accidental item correlations. With only 3 items we are investigating each item's idiosyncratic, unique, dimensionality.
Comment: The statistics are advisory, not mandatory. With only 9 items, you have a decision:
a. Do I want the less accurate, more precise measures produced by 9 items?
or
b. Do I want the less precise, more accurate measures produced by 6 items?
To make this choice, you need to think about the intended use of the instrument.
If it is to track individual change, then you need greater precision.
If it is to produce summaries of thousands of individuals, then you need greater accuracy.
With long instruments, the increased accuracy of stricter unidimensionality is usually more important than the loss of precision (loss of reliability) from decreasing test length. But with only 9 items, the standard errors of the person measures are probably large (and person "test" reliability is small). Reducing to 6 items will noticeably increase the person standard errors and reduce the person reliability.
mdeitchl:
Thank you, Mike! This helps me tremendously. In fact, I am most interested in accuracy than precision - as this instrument is not intended to be used for individual screening - only to report prevalences at a population level.
817. CAT Question
rblack November 20th, 2008, 2:47pm:
Hello again,
I hope it's okay, but I have another question! I'm trying to figure out if I should consider 1, 2, *and* 3-parameter models when developing a CAT version of a scale. Is there something unique to a CAT version that would lend itself to a Rasch (1 parameter model) approach only or would it be appropriate to consider all three models in terms of model fit?
Thanks!
Ryan
MikeLinacre:
Thank you for your post about CAT testing, Rblack.
If your CAT test is targeted correctly, then discrimination and guessing are difficult to estimate from the resulting CAT data. So Rasch (1-PL) is the practical option. There is almost no guessing, so 3-PL does not apply. 1-PL and 2-PL would give almost the same item difficulties.
If you are analyzing paper-and-pencil data to use the item difficulties in a CAT test, then, how about trimming the off-target responses? For instance, lucky guesses by low performers on difficult items will not happen in a CAT context (nor will careless mistakes by high performers on easy items), so there is no point in allowing the estimation process to skew the item difficulties to allow for these eventualities.
rblack:
Hi!
Thank you so much for responding! I hope it's okay, but I have a couple follow-up comments and questions.
I'm rating individuals on their level on a psychological construct (e.g. depression), and I don't believe I need the full set of items to accurately measure someone.
I understand the concept of item discrimination, but I'm struggling with how guessing would even apply to my situation. I'm thinking aloud for a moment, but I suppose guessing would be someone rating him/herself high or low on an item without any thought about the item (aka guessing?). I suppose that guessing wouldn't really be an issue with a CAT test, since a person would very rapidly return back to their actual state, even if they inadvertenly reported being high or low on an item. Am I correct so far? I also think you're recommending that I remove anybody who appears to be guessing from the analysis used to estimate item difficulties for the CAT. I'm not entirely sure how I'd do that in this context, but I understand the concept--remove extreme outliers (e.g. someone says he/she is suicidal, but reports being in a good mood every day). Does that sound correct?
So, 3-PL is out.
I'm now struggling with not considering a 2-PL model. I'm going to think out loud again. In CAT tests, we're not interested in item discrimination. We're only interested in item difficulty. Item discrimination is never incorporated into a CAT test. Am I correct? If yes, then I see your point. Even if I had a 2-PL model that provided a better fit (to the Rasch model), it would not be incorporated directly into the actual CAT test. Moreover, the actual item difficulty will change very little even if I added item discrimination. Might you have a reference for that observation? Are there any other reasons a 2-PL would not be recommended for this situation? Perhaps one needs to assume equal item discrimination in this context?
After writing this message, I think I understand your suggestions. I'm really sorry for the long follow-up response. I'd just like to make sure I'm not misinterpreting your comments.
I'm really looking forward to your response!
Ryan
MikeLinacre:
Ryan, thank you for your explanation.
3-PL is only for MCQ items, so 3-PL is out.
If you are using items with a rating-scale, then 2-PL is also out. It is only for dichotomous (2 category) items.
So your remaining options are polytomous Rasch models (Andrich rating scale model, Masters partial credit model, or one of the other Rasch models), or the IRT Generalized Partial Credit Model (which models varying item discriminations), or the Graded Response model.
rblack:
Thank you for responding, Mike!
I didn't realize that 2-parameter models were only used on dichotomous items. Anyway, your help has been invaluable!
Thanks again,
Ryan
818. Missingness?
rblack November 18th, 2008, 4:19pm:
Has anyone heard of the term, missingness, before in the context of Rasch/IRT modeling? If yes, what does this usually refer to? I'd really appreciate any help! Thanks, Ryan
MikeLinacre:
Googling - missingness rasch - produces 2,000+ hits.
Missingness seems to mean "missing data"
rblack:
Thank you for responding. I had googled the term with Rasch modeling as well. I figured it simply meant missing data, but wanted to make sure. Thanks again for confirming. -Ryan
connert:
Missingness refers to the way in which data are missing. See:
http://www.lshtm.ac.uk/msu/missingdata/understanding_web/node4.html
MikeLinacre:
Thanks for prompting us to look further, Connert.
http://en.wiktionary.org/wiki/missingness provides three meanings for "missingness": "absence", or "missing data", or "the manner in which data are missing from a sample of a population"
But, in practice, they probably all mean the same thing to the reader.
rblack:
Thank you both for responding. Very helpful. -Ryan
819. Winsteps analysis of subtests
aliend October 19th, 2008, 4:16pm:
I am setting up a control file for an assessment with 10 subtests. three very basic questions I am sure:
1) Two of the subtests have a 1-10 rating on a single item. Can I analyze these two single item?
2) Also subtests have various rating scales, some dichotomous and some polytomous. If I set these up using the group command is that sufficient?
3) Is it appropriate to set these all up in a single control file?
Thanks
MikeLinacre:
Thank you for your questions, Aliend.
1) A Rasch analysis must usually have more than one item. If there is only one item, there is not usually enough information in the data to construct linear measures.
2) Yes. Put all the valid data codes in CODES=, then specify the items in ISGROUPS= so that items with the same response structure have the same letters.
3) Yes, put everything in a single control file. Put a letter in each of the item labels to indicate its subtest. Then you can use ISELECT= if you want to include or omit subtests from your analysis.
OlivierMairesse:
About the analysis of a single item scale, I read an article where they use multifacets to assess the linearity of the response. In their case, one of the facets represents repeated measurements...
Improving Subjective Scaling of Pain Using Rasch Analysis
The Journal of Pain, Volume 6, Issue 9, Pages 630-636
K.Pesudovs, B.Noble
http://linkinghub.elsevier.com/retrieve/pii/S1526590005005948
Hope this helps,
Olivier
820. analyzing simulated rating data
brightle November 11th, 2008, 7:07pm:
Hi, I am trying to use FACETS(3.62) to analyze a series of rating data sets. with varying conditions of number of tasks and raters, in a fully crossed design.
I am wondering whether the FACETS would allow me to code all the command in one file (like batch), and run all in one shot.
I'd appreciate greatly if anyone would like to share the experience.
Thanks
Brightle
MikeLinacre:
Facets does support batch-mode operation, Brightie. Thank you for your question.
Please see: www.winsteps.com/facetman/batchyes.htm which is also in Facets Help.
brightle:
Hi Mike, thanks for your help.
Brightle
821. Some questions of a Rasch novice
RLS November 7th, 2008, 7:54pm:
1) Has Winsteps included the likelihood ratio test to compare two samples (e.g. male/female) for inspecting homogeneity? I know DIF, but this is to my knowledge only an investigation of several items. I want to investigate the whole scale. If yes, where can I find LRT and if not, has Winsteps something similar?
2) I have one study. In the first investigation (N=140) I have one time of assessment, so it is clear I have to use estimated Person Measure. In the second investigation I have from 20 persons also a second measurement; I want to look if there is a difference between the first and the second measurement (dependent sample). My question is now, which values should I use? Observed score (Totalscore) or estimated Person Measure (how do I get this values for the 20 Persons of the second measurement?)
3) Partial Credit model vs. Andrich Rating Scale Model: Is it right, that the applying of the Rating Scale Model is only correct if the response structure of the items of a scale (e.g. seen in the PCM) is very similar?
4) I have a test battery of 5 tests (160 items) and every test contains about 3-10 (more or less) independent subtests. Is it correct to analyse the subtest separately (N=140)?
Many Thanks!
RLS
MikeLinacre:
Thank you for your questions, RLS. Rasch measurement can be challenging to conceptualize.
1. LRT? - No. But you may be able to construct your own test from the Winsteps XFILE=. It contains the log-likelihood of every observation.
To compare the functioning of the test for two samples, one approach could be to do two separate analyses, and then to cross-plot the item difficulties.
2. Definitely the measures! In this design, the second measurement of the 20 persons would be analyzed along with the 140 of the first measurement. This would be an analysis of N=160. Put codes in the person labels for the 120 unique, 20 first time and 20 second time. Winsteps can then give you subtotals by group. Or you can do DIF by group. And you can export the measures to other statistical software to do whatever analyses you wish.
3. When comparing PCM and RSM, communicating the meaning of the rating scale is more important than the statistics of the PCM. For instance, if all the items have a conventional Likert agreement (SD,D,N,A,SA) rating scale. It would require very strong evidence to report these data using PCM. If some items are agreement and some are intensity. Then it makes sense to group the items with the same rating scale to share that rating scale. PCM was originally designed for partial-credit-scoring of MCQ items, where these is no expectation that the rating-scale structure will be shared between even two items.
4. Analysts have different approaches to subtests. Test constructors often perceive distinctions inside their tests which the responses do not reflect. So my approach would be to analyze all the items together to see how the analysis looks. There may well be such a strong dimension going through all the subtests that their variation from that dimension is at the noise level. You can investigate this using the Winsteps Dimensionality (PCA of residuals) analysis.
Hope some of these thoughts help. Anyone else - please share your thoughts too.
RLS:
All of these thoughts help! Many thanks!
1) LRT and log-likelihood. Is there somewhere an instruction?
2) Is it also correct to analyse (DIF etc.) the scales with the entire sample of 160 persons? I ask, because then 20 persons are double integrated (measure 1 and 2) in the data.
3) So I can apply RSM, even if the thresholds between the items are not the same.
4) The 5 tests have all a rating scale, but with different answering categories (3-7). So I can only apply PCM to analyse all the items together (N=160, Items=160 ?) or I can analyse the subtests of one test together. Is this thought right?
RLS
MikeLinacre:
Thank you for your further questions, RLS.
1. "LRT and log-likelihood. Is there somewhere an instruction?"
Winsteps reports the log-probability for each observation. These are summed and compared in log-likelihood tests. You need to specify the test, which will be a comparison of two log-likelihoods. Add up the log-probabilities into each log-likelihood. For more about LRT, google "likelihood ratio tests".
2. There may be dependency between the two instances of the 20 persons, but there are many possible sources of dependency within Rasch data. Consequently an approach is to analyze all the data together, and then inspect the local fit statistics to see whether the dependency is large enough to be of concern. If the dependency is large enough to skew your findings (or your think it might be), then analyze only the first measure for each person. Anchor the items and rating scale structures at the values from that analysis. Then estimate measures for each of the second measures using these anchor values.
3. Apologies, no. If the thresholds of the items are definitely not the same, then RSM is not a suitable model. RSM is only a suitable model if the thresholds may be the same across all items.
4. If the tests have different numbers of categories, then the rating-scale model (all items share the same rating scale structure) cannot be applicable. But PCM (every item has a different rating scale structure) may also be too extreme. Try to model together items which could share the same rating-scale structure:
log (Pnij / Pni(j-1) ) = Bn - Dig - Fjg
where g indicates a group of items sharing the same rating-scale structure.
OK?
RLS:
Thanks Mike!
I appreciate your effort and efficient answeres highly. Working with Rasch/Winsteps is really challenging and exciting. There are so many options to investigate data.
RLS
822. geometric mean of item discrimination
omardelariva November 3rd, 2008, 7:55pm:
Hello, everybody:
Winsteps makes an estimation of item discrimination in an assumed a 2-p irt model. Winsteps manual says that discrimination parameters are presented so that their geometric equal to 1.0.
How can I get the discrimination of items without this adjustment?
Thank you.
MikeLinacre:
Thank you for your question, omardelariva.
Let me clarify the Winsteps documentation:
1. Winsteps doesn't adjust for item discrimination (unlike 2-PL IRT models).
Winsteps does report an item discrimination index, which is computed in the same way that 2-PL estimates its discrimination "b" item parameter. But this discrimination index is merely reported (like the point-biserial correlation). It does not alter the person ability or item difficulty estimates.
2. The "geometric mean" is not forced on the reported discrimination indexes in Winsteps. They are each independently estimated. The "geometric mean" is a comment on the mathematics of item discrimination under the Rasch model.
But, in 2-PL, the 'b' parameters may be constrained to have a geometric mean of "1", e.g., by modeling them to fit a log-normal distribution.
OK?
823. Item bank
RS October 29th, 2008, 12:10am:
I have developed an item bank with 500 items. The initial analysis of this item bank revealed that there are not enough hard items. As a result, I have developed a test with hard to extremely hard items with some common items from the current item bank. This test was given to a sample of bright students.
I would appreciate your comments on the following issues:
1. The impact of using a non-systematic random sample on the item parameter estimates
2. The impact of adding these new items to the existing item bank
Many thanks
RS
MikeLinacre:
Thank you, RS.
1. The impact of using a non-systematic random sample on the item parameter estimates.
The problem is usually whether the items were responded to in a "high stakes" situation (little off-dimensional behavior by the respondents) or "low stakes" situation (much off-dimensional behavior by the respondents). If the situation is high-stakes, then the sampling procedure is usually irrelevant to the Rasch item difficulty estimates.
2. The impact of adding these new items to the existing item bank
Usually improves the bank, but please cross-plot the bank difficulties of the common-items against the difficulties of the items in a free analysis of the hard test. The line of commonality should parallel the identity line. It it does not, you may need to rescale the item difficulties of the hard test to match those in the bank.
824. What algorithm is used in Winsteps?
Andreich October 20th, 2008, 6:54am:
Hello! I am interested in the following question ... There are several algorithms to estimate the parameters of Rasch model: abilities of persons and difficulties of items!
What algorithm is used in Winsteps?
MikeLinacre:
Thank you for your question, Andreich.
The algorithm in Winsteps is Joint Maximum Likelihood Estimation (JMLE), also called Unconditional MLE (UCON). The parameters are estimated when (the observed score = the expected score) for each and every parameter (item difficulty, person ability, Rasch-Andrich threshold).
Andreich:
But how then to explain that Winsteps works with politomous data? JMLE (other name UCON) under the Best Test Design (chapter 3, p.62-65) handles only dihotomous matrix, where it can count the number of correct answers.
MikeLinacre:
Yes, initially there was considerable difficulty with polytomous data, Andreich. Georg Rasch proposed a model for those data, but it did not produce useful results. Then David Andrich proposed his polytomous model. It had not been implemented in software when Best Test Design was published (1979), but it had been by the time that Rating Scale Analysis (RSA, Wright & Masters, 1982, www.rasch.org/rsa.htm ) was published. It is the JMLE algorithm in RSA that is implemented in Winsteps.
Andreich:
Thank you for response! I'll try to look at information from the Rating Scale Analysis.
825. Looking for a Rasch consultant
soutsey October 13th, 2008, 12:45am:
Greetings,
I am looking for a consultant to run several analysis using Rasch. I am developing 2 measures; 1 measure of stress and 1 measure of academic stress. I need someone with reasonable fees and relatively reasonable turn-around time. Please email me at afropsych -/at/- aol.com. thanks.
Shawn
MikeLinacre:
Soutsey, thank you for your request. Perhaps you have already seen the list of consultants at www.winsteps.com/consult.htm
826. Category Reduction Question
baywoof October 10th, 2008, 4:11am:
A graduate student brought me a data set with 77 items using two rating scales: 5 points and 9 points. The analysis indicated category confusion, so we collapsed the items to 3 categories.
The Separation improved from 3.79 to 4.02 (Persons) and the Infit (Persons) improved from 1.12 to .91. The Outfit (Persons) got larger 1.11 to 1.21?
For the Item Separation, the value after collapsing was slightly worse while the infit improved and the outfit was worse.
Why would that happen? I assumed they would get worse or better together as the categories changed. :o
MikeLinacre:
Thank you for your questions, baywoof.
You are not specific about the nature of the category confusion, but let's imagine ....
Suppose that the 5 category rating-scale was a standard Likert rating-scale: SD, D, N, A, SA. Usually this is coded in order, such as 1,2,3,4,5. But suppose your student coded it 2,3,1,4,5.
The effect would be to decrease the predictability of the data or, in other words, to increase the unmodeled noise in the data.
Now it starts to get complicated ....
Rasch estimation rescales the logit measures to equalize the observed and expected randomness in the data. When the randomness in the data increases, the logit distances in the data reduce. Since the logit distances have changed, the average infit and outfit mean-squares should remain close to 1.0 (with or without the miscoding). An effect of the miscoding is usually to make the mean-square differences bigger between the overfitting measures (<1.0 i.e., not showing the effect of the miscoding) and the underfitting measures (>1.0, i.e., showing the effect miscoding).
Reliability = reproducibility of the item hierarchy. Separation = number of statistical strata in the distribution. Since the logit distances have been reduced as a result of the miscoding, the person (and item) reliabilities (and separations) generally reduce when there is miscoding.
But, the incorrect coding has changed the empirical definition of the item difficulties. The item difficulty is the point on the latent variable at which the categories coded highest and lowest are equally probable. The effect of the miscoding has been to change the item difficulty locations on the latent variable. So the effect on item reliability and separation is somewhat unpredictable.
Does any of this correspond to what you see? Or do we need to dig deeper .... ?
baywoof:
Thanks, Mike. You're correct that it was version of a rating scale, but some category descriptions were vague. Obviously, we didn't author the scale or it would have been clearer.
At the first pass, both the 1 to 5 and 1 to 9 items were changed to 1 to 3 using IREFER and IVALUE (11233 and 111222333) or similar strings after looking at the original item analysis. A few items (mostly the 1 to 9) had disordered categories that were "clumped" together and we hoped that collapsing would help, which it did. We may need to experiment with a few other recodes.
We set STKEEP=NO.
I'm still thinking about the decrease in infit while increasing outfit. I simply had not considered the change in "logit distances" and didn't expect the contrasting change between infit and outfit. I may have to play with some artificial data and see it happen before I really understand the dynamics because this is the first time that I remember seeing this. The only other times that I've collapsed categories, things got better (or they didn't) across the board. If I figure it out, I'll send something to RMT.
MikeLinacre:
Thank you for the explanation, Baywoof.
Please take a look at www.rasch.org/rmt/rmt101k.htm - that may have been a similar situation.
And please do send me a research note for publication in RMT.
827. different weights for the rating scale
bahrouni October 2nd, 2008, 4:34pm:
Hi,
I am measuring the rating of 31 EFL students' essays (1st facet) rated by 11 raters (2nd facet) on 2 elements in the category (3rd facet): Language Use (element 1) and Content (element 2). These 2 elements have different weights: Lge Use 18, while Cont. 12.
Could anyone tell me
1)how to enter those 2 elements in the control file and have FACETS account for that difference in the analysis.
2) whether FACETS supports decimals.
When I entered the decimals and ran the program, it gave this message: "Invalid datum, location ..., datum (9.5 for example) is too long or not a positive integer, treated as missing." For the time being, I've rounded up all decimals to get around the problem, but I know it's not as accurate as it is with decimals.
Thanks
Bahrouni
MikeLinacre:
Thank you for your questions about Facets, Bahrouni.
1. You can set the weights of the bobservations in the Models=
Models =
?, ?, ?, R3, weight
*
See "Data weighting" in Help at www.winsteps.com/facetman/models.htm
2. Facets doesn't support decimals. Multiply your observations by 2, then use a model-weight of 0.5 to adjust the raw scores back to their original range..
Comment about weighting:
Weighting distorts reliability computations, so report the reliabilities from an unweighted analysis.
bahrouni:
Thank you Mike.
This is what I've done:
?,?,?,R18,1,3
?,?,?,R12,2,3
where the maximum score for the first element of facet 3 is 18, while it is 12 for the second element of the same facet.
It seems it has worked! I'm still skeptical about the reliability of the category (3rd facet) though.
Examinee Measurement: Reliabilty .94 (very good)
Rater Measurement: Reliabilty .83 (quite good, still acceptable)
Category Measurement: Reliability 1 (? too good to be true! = sth might still be wrong?)
Pls have a look at the summary. Thanks
Table 7.1.1 Examinee Measurement Report (arranged by mN).
| Obsvd Obsvd Obsvd Fair-M| Model | Infit Outfit |Estim.| |
| Score Count Average Avrage|Measure S.E. | MnSq ZStd MnSq ZStd|Discrm| Nu Examinee |
-------------------------------------------------------------------------------------------------
| 235.1 22.0 10.7 10.51| -.01 .16 | 1.00 -.2 .98 -.2| | Mean (Count: 31) |
| 25.0 .0 1.1 1.09| .64 .00 | .68 1.5 .64 1.5| | S.D. (Populn) |
| 25.4 .0 1.2 1.11| .65 .00 | .69 1.5 .65 1.5| | S.D. (Sample) |
-------------------------------------------------------------------------------------------------
Model, Populn: RMSE .16 Adj (True) S.D. .62 Separation 3.88 Reliability .94
Model, Sample: RMSE .16 Adj (True) S.D. .63 Separation 3.95 Reliability .94
Model, Fixed (all same) chi-square: 482.3 d.f.: 30 significance (probability): .00
Model, Random (normal) chi-square: 28.3 d.f.: 29 significance (probability): .50
-------------------------------------------------------------------------------------------------
Training on FACET 10-03-2008 06:59:46
Table 7.2.1 Raters Measurement Report (arranged by mN).
Model, Populn: RMSE .10 Adj (True) S.D. .21 Separation 2.22 Reliability .83
Model, Sample: RMSE .10 Adj (True) S.D. .22 Separation 2.35 Reliability .85
Model, Fixed (all same) chi-square: 65.5 d.f.: 10 significance (probability): .00
Model, Random (normal) chi-square: 8.7 d.f.: 9 significance (probability): .47
-------------------------------------------------------------------------------------------------
Table 7.3.1 Category Measurement Report (arranged by mN).
Model, Populn: RMSE .04 Adj (True) S.D. .93 Separation 22.57 Reliability 1.00
Model, Sample: RMSE .04 Adj (True) S.D. 1.31 Separation 31.93 Reliability 1.00
Model, Fixed (all same) chi-square: 1020.7 d.f.: 1 significance (probability): .00
MikeLinacre:
Please check your model statements, Bahrouni.
I expected to see something like:
Models =
?,?,1,R18
?,?,2,R12
*
Now let's say some of your observations have 0.5 in them. Then
multiply all the observations in the data file by 2 before the analysis.
Models =
?,?,1,R36,0.5
?,?,2,R24,0.5
*
We expect the "category" items to be statistically very different in difficulty, so reliability=1.0 is a likely report.
bahrouni:
Hi Mike,
Thanks a lot for your helpful and prompt replies.
I've tried it both ways, and surprisingly I've got very different results:
1) ?,?,1,R36,0.5 (Data doubled = the '0.5' becomes 1)
?,?,2,R24,0.5
Examinee Measurement Reliability: .88
Rater Measurement Reliability: .66
Category Measurement Reliability: .53
2) ?,?,1,R18 (the same data rounded up = below 0.5 down, above 0.5 up)
?,?,2,R12
Examinee Measurement Reliability: .94
Rater Measurement Reliability: .84
Category Measurement Reliability: .92
Shouldn't these measures be the same in the 2 models as the first model is simply double the second?
I'm confused! I don'y know which model to take and why.
Thanks
Bahrouni
MikeLinacre:
Bahrouni, thank you for asking: "I don'y know which model to take and why."
This is very technical, and requires you to think about how the rating scales are intended to function.
The two models are not the same models. We expect that the rounded observations are less discriminating than the doubled observations.
Also, please look carefully at Facets Table 8 from each analysis. Verify that the unobserved category numbers are reported in the way you intend (as structural zeroes or incidental zeroes).
The Facets default is "structural zeroes", i.e., unobserved categories do not correspond to qualitative levels.
If you intend the unobserved categories to be "incidental zeroes", i.e., to correspond to qualitative levels, then the models are:
?,?,1,R18K (the same data rounded up = below 0.5 down, above 0.5 up)
?,?,2,R12K
and
?,?,1,R36K,0.5 (Data doubled = the '0.5' becomes 1)
?,?,2,R24K,0.5
Please look carefully at Table 8 from each analysis. Verify that the unobserved category numbers are reported in the way you intend (as structural zeroes or incidental zeroes).
bahrouni:
Hi Mike,
Thanks a lot for your invaluable assistance.
As you said, it's a very technical issue, and it's a bit difficult to grasp it from the first time. I'll have to do more reading to find more about it.
For the time being, I have those 2 models at hand to play around with. I'll definitely keep you informed of whatever I come up with or come across.
Your new ideas, great suggestions and comments are always welcome.
Once again, thanks a lot and God bless you.
A la prochaine
Bahrouni
MikeLinacre:
Good, Bahrouni.
Here is an example of "Structural zero" (unobservable) category, and "Incidental zero" (sampling zero) category.
Unobserved Categories: Structural Zeroes or Incidental (Sampling) Zeroes
Structural zero: A category cannot be observed, and is omitted from qualitative levels. (The default.)
Model = ?,?,R3
+------------------------------------------------------------------------------------------------------------+
| DATA | QUALITY CONTROL | STEP | EXPECTATION | MOST |.5 Cumultv| Cat| Obsd-Expd|
| Category Counts Cum.| Avge Exp. OUTFIT|CALIBRATIONS | Measure at |PROBABLE|Probabilty|PEAK|Diagnostic|
|Score Used % % | Meas Meas MnSq |Measure S.E.|Category -0.5 | from | at |Prob| Residual |
|----------------------+-------------------+-------------+---------------+--------+----------+----+----------|
| 0 378 20% 20%| -.87 -1.03 1.2 | |( -2.04) | low | low |100%| -.9 |
| 1 620 34% 54%| .13 .33 .7 | -.85 .07| .00 -1.17| -.85 | -1.00 | 54%| |
| 2 | | | | | | | | <= Structural zero - no count shown
| 3 852 46% 100%| 2.23 2.15 1.5 | .85 .06|( 2.05) 1.18| .85 | .99 |100%| |
+------------------------------------------------------------------------------------------------------------+
Incidental zero: A category can be observed (but not in this dataset). It is included in the qualitative levels. (Keep.)
Model = ?,?,R3K <= K means "Keep unobserved intermediate categories"
+------------------------------------------------------------------------------------------------------------+
| DATA | QUALITY CONTROL | STEP | EXPECTATION | MOST |.5 Cumultv| Cat| Obsd-Expd|
| Category Counts Cum.| Avge Exp. OUTFIT|CALIBRATIONS | Measure at |PROBABLE|Probabilty|PEAK|Diagnostic|
|Score Used % % | Meas Meas MnSq |Measure S.E.|Category -0.5 | from | at |Prob| Residual |
|----------------------+-------------------+-------------+---------------+--------+----------+----+----------|
| 0 378 20% 20%| -.68 -.74 1.2 | |( -1.99) | low | low |100%| 1.0 |
| 1 620 34% 54%| -.11 -.06 .6 | -.90 .07| -.23 -1.09| -.90 | -.95 | 56%| -.7 |
| 2 0 0% 54%| | | .63 .24| | .55 | 0%| | <= Incidental zero (count shown as 0)
| 3 852 46% 100%| 1.35 1.34 1.7 | .90 .07|( 1.50) 1.10| .90 | .55 |100%| |
+------------------------------------------------------------------------------------------------------------+
bahrouni:
Thanks Mike.
I'm trying to digest this big bite.
You know what, the more I read about Rasch, the more bits and pits I discover. Some are abysses, not even pits! The important thing is that I'm enjoying it. Isn't confusion the beginning of true learning, as somebody once put it??
Thanks a lot
A la prochaine
Bahrouni
828. Separate vs Concurrent calibration
RS September 24th, 2008, 7:00am:
Two language tests with equal number of items are given to the same students (n = 500). The first test (Spelling) contains 50 multiple choice items while the second one (Grammar) consists of 50 short response items (0 incorrect & 1 correct). Two steps were taken to analyse the data:
In the first step, each test was calibrated separately using RUMM software. The results indicate that there are only three under-discriminating items in the Grammar test. There is no misfitting item in the Spelling test.
In the second step, two tests were calibrated simultaneously (with 100 items) to construct a single language scale. The results of this analysis signify that data do not fit the Rasch measurement model. There are 24 misfitting items (item fit residual greater than 2.5 or smaller than -2.5 with a chi square probability smaller that 0.01). More specifically, there are 8 over-discriminating spelling items and 16 under-discriminating Grammar items.
My questions are:
1. Why the combined data set does not fit the Rasch model?
2. Do Spelling and Grammar tests measure different construct?
3. Do the ICC of multiple choice and dichotomous items have a different slope?
Many thanks in advance
RS
MikeLinacre:
This is an instructive analysis, RS.
You have two well-behaved tests, but their combination is not so good.
Here is a suggestion: obtain the person ability measures from the two separate analyses and cross-plot them.
A. Do the points on your scatterplot form a statistical line or a cloud? If they form a cloud, then spelling and grammar are different constructs. So combining them would not fit a Rasch model.
B. If they form a line, is it parallel to the identity line. Does it have a slope of approximately 1? If the slope is near 1, then the concurrent calibration should have worked well.
If the line is not parallel to the identity line, then you have a Fahrenheit-Celsius situation. The two tests could be measuring the same construct but with different test discriminations. Concurrent calibration won't work, but the results of the two tests can be compared in the same way that we compare Fahrenheit and Celsius termperatures.
Multiple-choice items are usually scored (1 correct option, 0 incorrect options) so they are a type of dichotomy, but constructed-response dichotomies are usually much more idiosyncratic (noisy, subject to over-dimensional behavior) than MCQ dichotomies. This means that the CR items tend to be less discriminating than MCQ items. In general, the MCQ dichotomies would have a steeper slope than CR dichotomies. So, when combined in one dichotomous Rasch analysis (where all items are modeled to have the same discrimination), we would expect the MCQ (spelling) items to be over-discriminating, and the CR (grammar) items to be under-discriminating - which matches what your report.
OK? Does this help?
RS:
Thanks a lot Mike. It certainly helped.
I have plotted the person ability measures from the two separate analyses and found that the points on scatter plot form a cloud (Pearson correlation is 0.71) rather than a line. As you have mentioned, it means that spelling and grammar are two different constructs. So combining them would not fit a Rasch model.
RS
MikeLinacre:
RS, to be extra sure, you could disattenuate the correlation:
revised correlation = observed correlation / sqrt (reliability(grammar)*reliability(spelling))
This will indicate whether the 0.71 is due to a difference in constructs or measurement error. www.rasch.org/rmt/rmt101g.htm
RS:
Disattenuated value is .98 indicating that measurement error is randomly distributed.
Thus, I decided do not combine the Spelling and Grammar tests as they measure different constructs.
Many thanks.
MikeLinacre:
RS, a disattenuated correlation of 0.98 indicates that the relationship between the variables is almost 1.0, after adjusting for measurement error. This is about as good as it gets!
You research is giving contradictory findings about the relationship between Spelling and Grammar. This suggests that a closer investigation is required. In particular, that a wider range of person-ability needs to be tested.
829. DIF vs mean differences in item responses
mve September 4th, 2008, 2:37pm:
Hi. I am trying to understand the advantage of Rasch for DIF across groups vs. comparing mean differences in item responses. In an article it says:
'Rasch models remove the effects of person ability and developed item difficulty ratings for each group separately. Thus, differences in total scale score, or person effects, are removed when comparing item difficulty estimates'.
Unfortunately, I'm new to Rasch and can not fully understand it. I have tried using Winsteps Help but still confused. I would appreciate your help.
Thanks
Marta
MikeLinacre:
Marta, there are two aspects to this. Let's compare boys and girls:
1. Overall, boys are stronger than girls, so boys will do better on a weight-lifting test. This is not DIF. This is a difference in the mean strengths of the two groups.
2. If weight-lifting items are included with other items on an athletics test including running, jumping, etc., boys will do better than girls on average. That is not DIF. Boys are better at athletics than girls.
But boys will perform especially well on the weight-lifting items. That is DIF. Because the weight-lifting items are relatively easier for boys than for girls, after adjusting for their overall performance levels of the two groups.
Does this help? Can anyone think of a better example?
Raschmad:
Hi Mike
This is a clear example
you wrote:
"after adjusting for their overall performance levels of the two groups"
Can you please explain about the technicalities and how this is done in Rasch and in Winsteps?
Thanks
MikeLinacre:
Certainly, Raschmad.
Please see www.winsteps.com/winman/difconcepts.htm - look down the webpage at "The Mathematics of Winsteps DIF and DPF Estimation"
RLS:
Thanks for the great forum!
I have also a question to DIF:
Inspect the Likelihood-Ratio-Test (Andersen, 1973) the same as DIF?
RLS
MikeLinacre:
RLS, the Andersen LRT appears to be equivalent to a test of non-uniform DIF for the entire sample. It appears that it could be reformulated into a uniform DIF test for different sub-samples. Other researchers may have done this, because Cees Glas refers to LRT DIF tests in Fischer & Molenaar, "Rasch Models".
mve:
Hi Mike. I have another question about the two types of DIF: uniform vs. non-uniform. Do you always need to investigate for both of them? In such case, how do you know how many levels of ability to specify in the non-uniform (e.g. MA2 - 2 levels). Thanks Marta
MikeLinacre:
Uniform DIF is much easier to quantify, and to remedy if discovered, than non-uniform DIF, Marta.
If non-uniform DIF is identified, there is no simple remedy (that I know of), other than to make responses to that item for the disadvantaged group into missing data.
The number of ability levels is a matter of the analyst's choice, but I would look at the empirical ICCs for each group first to see how often they cross the model ICC. If the number of levels contradicts the shape of the empirical ICCs for a group then non-uniform DIF may be undetected or over-detected.
830. Response-Structure ISFILE
mve September 12th, 2008, 3:48pm:
Hi Mike. I wonder if you can clarify this for me. I have a 5-point scale. To produce a table of expected measures per item-category I look at the output from ISFILE. From the Winsteps help I understand that I should use the column CAT+0.25 (for 1st category) and AT CAT for the remaining categories. However, I do not have an AT CAT column for my last category. Should I use CAT-0.25 for the last category only? I beleive so but would appreciate your help once again...
Marta
MikeLinacre:
Yes, mve, CAT-0.25 is a measure which usefully represents performance in the top category of an item.
mve:
Mike, Thanks for your help.
831. Over Discrimination items
RS September 12th, 2008, 6:19am:
I am new to this Forum and would like to ask a question regarding item discrimination.
What would you do with over discriminating items?
Regards
RS
MikeLinacre:
Thanks for your question, RS.
What you do with over-discriminating items depends on where you are in the test-development-and-use cycle.
If this is a pilot item (brand-new item under test), then the high discrimination probably means that it duplicates other items or incorporates another variable (for instance, a math item with a high reading-comprehension component).
If you are reporting test scores on a production test, then the over-discrimination will have little influence on the meaning of the measures (it is like asking the same question twice). So it is probably less trouble to leave the item in the test than to remove it from the test, and then have to explain to CTT folk why you omitted their "best" item.
What is your situation?
RS:
Thanks Mike.
I am trialing 60 new Maths items and expecting to have 45 items in the final form.
MikeLinacre:
Thanks for the info., RS.
Take a look at those over-discriminating items. We can usually identify why they over-discriminate ...
Are they almost identical to other items on the test?
Do they summarize other items?
Are they double-items (it takes two steps to come to an answer)?
Do they rely on external information (e.g., knowledge of baseball, the metric system, reading ability)
832. Item-trait interaction (chi square)
mve September 9th, 2008, 2:58pm:
Hi again... I notice that some recent publications in my field of research report overall fit of the data to the Rasch model using item-trait interation (chi square) values (with RUMM software). Does Winsteps also report this fit statistics? Otherwise, which statistic would report similar information with Winsteps? I apologise if this question is too basic but I am trying to understand why different statistics are reported in different studies... Thanks Marta
MikeLinacre:
Certainly, Marta.
The item-trait interaction chi-square is a standard statistic in RUMM2020. It reports the interaction between item difficulty and person ability-level, i.e., non-uniform DIF for the sample. Usually there are 4 or 5 ability levels.
You can obtain equivalent statistics in Winsteps by doing a DIF analysis specifying DIF=MA4 and then looking at Table 30.4.
The item-trait interaction chi-square summarizes the empirical ICC. So, first, look at the empirical ICC on the Graphs menu. You will then know how strong is the interaction reported by the chi-square (which reports statistical significance, not substantive size).
833. Winsteps version 3.35
mve September 3rd, 2008, 3:35pm:
Anyone with Winsteps version 3.35 having probs calculating DIF? The table that I get does not have t values. Is there any extra specification that I should provide to get t values? Otherwise, how can i tell whether the differences are significantly different?Many thanks
Marta
MikeLinacre:
Thank you for your questions, Marta.
According to www.winsteps.com/wingood.htm, Winsteps 3.35 was released in July 2002. The current version is 3.66 - released Sept. 2, 2008.
Sorry, I don't have 3.35 installed on my computer, but I do have Winsteps 3.32. It reports a t-statistic column in Table 30.1. The Help file for 3.32 suggests that this value can be interpreted as a unit-normal deviate (when sample sizes are large).
What do you see in your Table 30.1?
Current versions of Winsteps provide considerably more DIF-related output in Table 30 and its subtables. They are linked from www.winsteps.com/winman/outputtableindex.htm
mve:
Thanks for your reply. I have tried Ministep and noticed the improvement in DIF tables. I will most likely update my Winstep version.
834. person ability and item difficulty
barman September 4th, 2008, 8:35am:
Can any one help me how to calculate (not estimate) person ability and item difficulty not by using FACETS or WINSTEP?
MikeLinacre:
Thank you for your question, barman.
Other computer software (much of it free) is listed at www.winsteps.com/rasch.htm
If you want to write your own computer software, then Wright & Stone "Best Test Design" includes some practical algorithms for dichotomous data, including a simple one that you can do by hand. For polytomous data, see Wright & Masters "Rating Scale Analysis".
835. Principal component analysis
vijaya August 26th, 2008, 10:34am:
Hi all,
I am trying to detect evidence of mulitidimensionality in the persons. I am using Winsteps version 3.57.2 and cannot obtain the "table of standardized residual variance in Eigenvalue units)". I would appreciate any advise on this.
Thanks,
Vijaya.
MikeLinacre:
Thank you for your request, Vijaya.
In Table 23.2 you should see something like this:
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
Empirical Modeled
Total variance in observations = 1482.9 100.0% 100.0%
Variance explained by measures = 1468.9 99.1% 98.6%
Unexplained variance (total) = 14.0 .9% 1.4%
Unexpl var explained by 1st factor = 2.7 .2%
The first column of numbers is in Eigenvalue units, but they are too big.
Developments since Winsteps 3.57 indicate that this Table computed with raw residuals PRCOMP=R gives more accurate sizes to the variance components:
Table of RESIDUAL variance (in Eigenvalue units)
Empirical Modeled
Total variance in observations = 49.2 100.0% 100.0%
Variance explained by measures = 35.2 71.6% 71.0%
Unexplained variance (total) = 14.0 28.4% 29.0%
Unexpl var explained by 1st factor = 2.7 5.6%
vijaya:
Thanks very much for the reply Dr. Linacre. Now does this mean that I will have to use the higher version (3.65) of Winsteps to obtain the table of residual variance. Please advise.
Vijaya.
vijaya:
Thanks for the reply Dr. Linacre. I am sorry for my earlier email asking if I needed to upgrade to a higher version of Winsteps. I have now been able to obtain the table of residual variance for persons. However I need to know the total variance explained by all the 5 factors together in a single table. In the help menu of Winsteps such a table showing variance explained by 5 factors exists but I am not able to obtain it. Please advise if such a table does exist in the current version that I am using..
MikeLinacre:
Sorry, Vijaya, not in that version of Winsteps. But you can copy-and-paste the pieces from the 5 variance tables to make one complete variance table.
vijaya:
Thanks very much for the reply, Dr. Linacre. I have been able to do as suggested and obtain the information.
836. Some questions on facets of assessment
limks888 August 27th, 2008, 7:57am:
Hi Mike,
I've read some articles on the multi-facets Rasch model. Most of them listed rater severity or leniency as a facet, besides item/task difficulty and student ability.
My question is :
If I want to use different assessment inventories/tests to assess the presence of a latent trait of , say, physics literacry e.g., quantitative item based test and qualitative item based test, etc. Can test type be considered as a facet?
Regards,
Lim
MikeLinacre:
Thank you for your question, Limks888.
In your design, your test items are probably nested within test-type.
So you would need to make a decision:
A. Is "test-type" a dummy-facet which is not used for measurement, but only for producing summaries. Each item within the test-type has its own difficulty.
or
B. Does "test-type" have a difficulty, so that the difficulties of the items within the test-type are relative to the test-type, i.e., the sum of the difficulties of the items within the test-type is zero relative to the difficulty of the test-type.
limks888:
Thanks for your answer Mike,
Correct me if I'm wrong. You mentioned that for decision B,the sum of the difficulties of the items within the test type is zero relative to the difficulty of the test type. Is the purpose to eliminate the item facet from the measurement model without changing the estimates for the ability and test type facets?
Kindly elaborate.
Regards,
lim
MikeLinacre:
Limks888, you asked: "Is the purpose to eliminate the item facet from the measurement model?"
No, it is make the measurement model function. It is:
Ability + test-type + item = Observation
Since items are nested within test-type, we can add anything to a test-type provided we subtract the same amount from the items. So we must constrain test-type or item. A convenient constraint on the items is to make their difficulties be relative to the test-type. If we do this, then the sum of the item difficulties within test-type is zero.
837. DIF Computation
Raschmad August 23rd, 2008, 7:16am:
Dear Mike,
In table 30 of WINSTEPS there are person calsses, DIF measure for each class, their difference and the statistical significance of this difference. How do we know that statistically significant differences are not due to real diffrences in ability of the two classes?
How does Winstpes make sure that the ability groups- for computing DIF measures for an item in each class- are equally able?
Thanks
MikeLinacre:
Thank you for your question, Raschmad.
DIF is computed after adjusting for differences in overall classification-group ability. The classification-groups are not expected to be of equal ability, but that does not matter.
For more details, please see Winsteps Help "DIF Concepts"
838. Sample Size Questions
jinbee July 31st, 2008, 9:07pm:
Hi Mike,
I appreciate the help you've given me in the past (and to others...I have learned a lot from reading through other threads), and was hoping you might be able to provide some insight into a few sample size questions I have.
I read through other posts about sample sizes and read the "Sample Size and Item Calibration [or Person Measure] Stability" article: https://www.rasch.org/rmt/rmt74m.htm
but didn't find all the answers I'm looking for. I'm working with dichotomous data and I'd like to know:
1. Is item parameter estimation problematic if you have more items than people? e.g., 100 items and 30 people? From the article it seems that 30 items administered to 30 persons should produce statistically stable measures, and I know there is no problem calibrating 30 items administered to 100 persons, but I'm not sure about the other way around. The article says, "The Rasch model is blind to what is a person and what is an item..." so is that my answer? It doesn't matter what number you have of each as long as it is above 30/30?
2. Does the minimum of 30/30 only hold for the 1PL, or can that be extended to the 3PL?
3. Are there any extra considerations to make regarding sample size when you're working in a high-stakes environment? e.g., passing or failing a student, granting a license or certifying an individual
Thanks for your consideration!
MikeLinacre:
Thank you for your questions, Jinbee.
For the Rasch model, any rules for items are the same for persons. However, 30 by 30 is a very small dataset. Some work by a colleague indicates that at least 250 persons are needed for a high-stakes situation.
3-PL estimation is very unstable. Authors in that area suggest that samples of thousands of persons are required. The lower asymptote will probably need to be imputed, not estimated.
jinbee:
Hi Mike,
Thanks so much for your thoughts on the situation. Do you happen to have any references that would provide more information on what you shared?
Thanks!
MikeLinacre:
Does anyone know of any good references about sample size? Please post them here.
winderdr:
Sample Size for Stable Rasch Model Item Calibrations
Item Calibrations stable within Confidence Minimum sample size range
(best to poor targeting) Size for most purposes
± 1 logit 95% 16 - 36 30
± 1 logit 99% 27 - 61 50
± ˝ logit 95% 64 - 144 100
± ˝ logit 99% 108 - 243 150
839. Unfolding IRT models
connert August 13th, 2008, 1:06am:
Does anyone know if these models:
http://www.psychology.gatech.edu/departmentinfo/faculty/bio-JRoberts.html
produce true interval scales? Are there references to support whether they do or don't?
MikeLinacre:
Thanks for the question, Connert.
Unfolding models cannot produce mathematically-rigorous interval scales, in the way that Rasch models can, but unfolding models can produce approximately interval scales. And, for almost all purposes, approximately-interval scales are good enough.
Folded data (such as "Are we spending the right amount on food?" Yes/No) incorporate ambiguities. Where possible, generate unfolded data("Are ... food?" Too little/About right/Too much).
840. Anchoring Raters
jimsick July 27th, 2008, 9:09am:
Mike, I have a data set where 8 interviewers provided a single holistic oral proficiency interview to 100 examinees. One interview per examinee, so single observation, no overlap. On the same day, all examinees took a second speaking test in a group discussion format, this time observed by two raters. I've constructed measures from the discussion test. Now I'm wondering if there is some way i can use that data to anchor or link the interview and construct measures for that.
Tried anchoring the interview examinees to the measures derived from the discussion to estimate the interviewers' severity. Worked great. Very clear who the tough interviewers are.
Next tried to run the interview data with the interviewers anchored and examinees free. But it wouldn't run. (Error F36: All data eliminated as extreme). I assume this is because there is only one observation per person?
Tried adding the interview scores as an extra item (observed only by one) to the discussion test analysis. Works, but there is no way to recover just the interview, which is what I'd like.
Any ideas?
MikeLinacre:
This is very thin data, Tko-jim. It seems you want a measure based on only one observation. This will have huge imprecision.
In your "extra item" analysis, a possibility would be to do an examinee x item bias analysis in the Output Tables menu. Then look at the Excel plot.
The "Absolute Measure" for the examinees would be what you want.
841. Anchoring
limks888 July 23rd, 2008, 2:34am:
Hi Mike,
Hope you can help a Rasch novice like me.
I read that when data are 'stacked', each person is assessed twice, that is, before intervention and after intervention. Moreover these two sets of observations need to be converted into measures in the same frame of reference. What does this actually mean? Also what is meant by 'measure at time 1, anchor at time 2' and vice versa. Any underlying theory on this? Any suitable reference recommended?
Thank-you,
Lim
MikeLinacre:
Thank you for your questions, Lim.
If someone is assessed twice, then we have two data records for that person.
When those data are "stacked", they are treated as independent data records in the analysis (two cases in the datafile). When the data are analyzed, then the measures estimated from the two data records will be in the same frame of reference. This means that the two measures for that person are directly comparable, exactly the same as if we had weighed the person twice.
If we assess the person at two time-points, "admission" and "discharge", or "pre-treatment" and "post-treatment", or "beginning" and "ending", often one of the time-points is more important than the other. For medical applications, treatment decisions are made at admission. For educational applications, certification is made at completion of the training.
If one time-point is much more important than the other, we may want to calibrate the item difficulties at the important time-point, and then impose these difficulties on the less important time-point. This is done by "anchoring". We estimate the item difficulties only from the data records for the important time-point. Then anchor (fix) these difficulty measures, and measure the performances at the other time point.
To find a reference, Google - Rasch anchor -
That gives a useful list of places to look.
limks888:
Thanks Mike for you reply.
After some additiional reading, let me try to figure out what you mean.
When you said that " ... we estimate the item difficulties only from the data records for the important time-point. Then anchor (fix) these difficulty measures, and measure the performances at the other time point"
does this mean that we can use the 'equating constant procedure' such that the item difficulties for the anchor test items on the other time point are subtracted from their corresponding anchor item difficulties on the important time point; summed and divided by the total number of anchor test items”?
Another question is if the the persons sat for the same test items at the two time points, doesn't it mean that all the items are now anchor items,, instead of a smaller common set of anchor items in the two tests?
Moreover is it possible for the same group of persons to be considered as two independent groups?
Regards,
Lim
MikeLinacre:
Sorry for my ambiguity, Lim. Here is what I mean ...
"Common items" = items on both tests.
"Anchor items" = items in one test whose difficulty measures are anchored at the estimate provided by a common item in the other test.
So, we analyze the first test, and obtain the item difficulties.
Then we find the common items in the second test, and anchor the difficulties of the common items in the second test at the difficulties of those same common items in the first test.
There is no "summing and dividing".
842. Correlation between logit measures
limks888 June 30th, 2008, 6:18am:
Hi Mike,
Pls help me on this.
Distributions of person abilities in logits, and of item difficulties in logits have interval scales of measurements. Is it possible for me to do the following:
1. Using the Pearson-r correlation to look at the relationship between distributions of person ability (in logits) on two different tests?
2.Can parametric tests, say of ANOVA, t-tests, etc be used for distribution of logit measures - will the assumptions for use of these tests be met?
Still learning!
Lim
Raschmad:
hi Lim,
when people use all these tests and analyses with raw scores, then why not with interval scale measures?
Raschmad
MikeLinacre:
In fact, most of these statistical operations assume that the numbers being analyzed are interval measures, so those operations should work better with Rasch measures than with raw scores.
limks888:
Thanks Mike, Raschmad for your quick replies,
One thing though, when Mike said "statistical operations work better with Rasch measures than wtih raw scores" what do you actually mean by working better. Do you mean the power of the statistical tests are improved? or there is less measurement error if the test is comparing measures on, for example, a pscyhological construct?
Lim
MikeLinacre:
Typical statistical tests do not account for the non-linearity of the numbers they are analyzing, such as the floor- and ceiling-effects inherent in raw scores. Accordingly the results of those statistical tests can be misleading.
An example is in the use of raw scores to track gains. The curvi-linear nature of raw scores produces findings such as "average gains by high and low scorers were small, but gains by middle scorers were high", even when high and low scorers may have gained more along the latent variable than middle scorers.
limks888:
Thanks Mike,
It is clear to me now.
Lim
843. Computing degrees of freedom
Michelangelo June 28th, 2008, 2:35pm:
Hi!
I can't figure out how to compute degrees of freedom when I compare two elements of the same facet.
Suppose I have 3 facets: 116 subjects, 20 items, and 2 conditions (time 1 and time 2).
I want to compare measures of item #1 and item #2 so I take the differenze between their measures and then I divide this difference by the joint std error. In this way, I should get a t, right? If so, how many degrees of freedom does this t have? I know it's N-1 + N-1, but the question is: N is the number of elements or the number of observations (observed count)?
In my example, at a first time, I thought df were equal to 20-1 + 20-1 = 38. But then, I thought that maybe I should look to observations, not elements. In this way, df would be equal to 232-1 + 232-1 = 462.
Quite a big difference...
I would really appreciate if someone can take me out of this dilemma :-)
MikeLinacre:
Thank you for your question, Michelangelo.
In principle, the d.f. for the comparison of two element measures is the number of "free" observations: (sum of observations for the two elements - 2). But there are other considerations, such as the interdependence of estimates and also misfit of the data to the model. So a conservative position would be to half the d.f. when estimating significance.
So, in your example, the highest possible d.f. for the comparison of 2 items is 2x(116 -1) = 462, giving p<=.05, t= 1.965.
If we take the conservative position, d.f. = 462/2 = 231, p<=.05, t=1.970.
This difference is very slight, so t=1.97 as a significance value is reasonable.
Your other d.f. = 20-1 = 19 would refer to an estimate of the mean of the item difficulties.
844. CAT
Raschmad June 11th, 2008, 6:20pm:
Hi Mike,
I want to use CAT for an English placement test.
My understanding of CAT is that one first calibrates a large pool of items. Using an equating technique the difficulty estimate of all these items are estimated on a common scale.
Then the items are put in an item bank. A computer programmes is written and the formula for estimating ability measures with known item difficulty is implemented in the programme (your paper in RMT) and the ability of test-takers is estimated based on the number of items they reply, the difficulty of the items they encounter and the formula. Is that right?
Cheers
MikeLinacre:
The technique your describe for CAT item-bank construction is widely used for high-stakes testing, particularly those originating in paper-and-pencil tests.
But you may find it more convenient to start with a small bank of calibrated items, then introduce new items as you go along. This is easy to do in CAT testing. Administer one or two pilot items (from your pool of pilot items) to the test-takers as part of the test. The pilot items are not used for ability estimation. Then when you have calibrated each pilot item, make it a live item. This way, you can bring new items online easily, and also drop old items that no longer function as intended (e.g., through over-exposure).
Your description of the ability estimation is correct. It is done after each item is administered so that a usefully-targeted next-item can be selected.
drmattbarney:
[quote=MikeLinacre] This is easy to do in CAT testing. Administer one or two pilot items (from your pool of pilot items) to the test-takers as part of the test. The pilot items are not used for ability estimation. Then when you have calibrated each pilot item, make it a live item. This way, you can bring new items online easily, and also drop old items that no longer function as intended (e.g., through over-exposure).
Your description of the ability estimation is correct. It is done after each item is administered so that a usefully-targeted next-item can be selected.
Mike,
What is your opinion of a few alternative ways of using new items such as
a) Using a Facets approach to get experts to estimate item logits (adjusting for severity/leniency
b) Using Yao's approach https://www.rasch.org/rmt/rmt52b.htm
Instead of holding items out for the time being. On a related note, do you have a recommendation for Rasch-CAT on the web (not on a PC)?
Matt
MikeLinacre:
Glad you are involved, Matt.
Yes, to get a CAT system started "from scratch", use reasonable "theoretical" item difficulties, and then adjust them as the empirical data comes in. In the re-estimation process, maintain the person mean (not the item mean) and few ability estimates will change noticeably. And then re-estimate item difficulties every month or every 1,000 persons, or whatever - again maintaining the person mean.
CAT on the web and the PC can be identical if the CAT routine is written in Javascript or some other transportable language. You may want to download part of the item database (selected and encrypted) to the end-user as part of the test initialization. This avoids having to communicate with the user after every response. The response string would be uploaded when the test completes.
drmattbarney:
Hi Mike
As usual, thanks for the fast, cheerful and useful reply. Are there any commercial web-based CAT programs that would avoid me writing javascript (I'm not a good programmer)
Matt
845. Anchoring when disordered
ning May 20th, 2008, 5:37pm:
Hi Mike,
In your stacking approach, what if I end up with a set of threshold values that are disordered? Should I "fix" them and make sure they are ordered before I use them as anchor values in stage III?
Thanks.
MikeLinacre:
Thank you for your question, Gunny.
If the Rasch-Andrich thresholds are disordered, then some of your intermediate categories have relatively low frequencies. This means that they correspond to intervals on the latent variable too narrow to become modal (distinct peaks on the probability-curves plot).
What you do depends on how you conceptualize your rating scale. If your rating scale categories must all be modal, then you need to combine each narrow category with an adjacent category. Use the "Average Measures" to do this. Combine the category with the adjacent category with the nearest "average measure".
For most applications, modality of categories is not required, though it is generally desirable. Exceptions include rating scales with categories such as "Don't know". We like this category to be as narrow as possible, so we expect it to have disordered thresholds.
ning:
Dear Mike,
Thank you for your reply. I'm sorry I'm still not clear...say, I'm conducting a retrospective data analysis....data collected using existing instruments...assume my thresholds are disordered and I did according to what you suggested..........if I have 10 items, each with 5 categories, so 4 thresholds...if 3 of the items had disordered steps and I collapsed them accordingly...so they end up with only 3 or 2 steps, how do I anchor the "altered or reduced" step values to recalibrate the items that all have 4 steps values?
Thanks, Mike.
MikeLinacre:
If you collapse categories, Gunny, you have changed the structure of the data. You have to go back and re-analyze. Another reason not to collapse unless it is essential to the meaning of your measures ....
ning:
Thanks, Mike, This leads to the question of a series of missing data questions that have been puzzling me.
1) In your FACET user manual, page12, you stated that Rasch models are robust against missing data...are you referring to missing observations or missing categories? Are all missing data assumed to be missing at random?
2) In your "Many-Facet Rasch Measurement" book, page 67-68, you stated "If a category were missing from the empirical data, the structure of the rating scale would change and consequently the estimates of the parameters would be biased....No estimated algorithm takes account of the probabilities of empty categories...." Could you please clarify these statements?
3) Again in FACET user manual, page 214, treating missing data as either incidental or structural zeroes....how do I determine whether I should treat the miss in my data incidental or structural? What's the criteria? If I don't take this step, will the estimates still robust? or will the estimates be biased? Does 'ORDINAL" approach equivalent to collapsing the categories?
Sorry about the long email, your help is greatly appreciated!
MikeLinacre:
Important questions, Gunny.
1. "robust against missing data" - means that most incomplete data designs are acceptable. I have successfully analyzed datasets with 99+% missing data.
Data are not assumed to be missing at random. Missing data are merely omitted from estimation (skipped over).
2. Missing (unobserved) categories. These are always a problem. The analyst must make some assumption about how they relate to the observed categories. If they could be observed in another dataset, then they are incidental, sampling zeroes. If they could never be observed, then they are structural zeroes.
If they are structural zeroes, the best solution is to recode the data (Rating scale=) to remove them. If they are incidental intermediate categories, then "Keep". if they are incidental extreme categories, then the best solution is to include some dummy data records in which they are observed.
3. The Facets default is to treat all missing categories as structural and to renumber the categories ordinally from the lowest category upward.
"collapsing categories" is done through recoding two categories to have the same ordinal value, e.g., with Rating scale=
ning:
Thanks, Mike.
1) What's the best way to include the dummy data records in which they are observed for incidental extreme categories? And, are there different ways to handle this in Facet as opposed to in Winsteps?
2) For your #3, can I understand..."The Facets default is to treat all missing categories as structural and to renumber the categories ordinally from the lowest category upward," unless I manually specified it's incidental missing, correct? Does the Winsteps has the same default approach on this matter?
Thanks again.
MikeLinacre:
Gunny, Winsteps and Facets are the same on both questions.
1. Dummy records: include in the data file some reasonable records which include both extreme incidental and non-extreme observations. Usually only two records for a dummy person are needed. These will produce too small an effect to alter substantive findings.
2. The default in Facets is to renumber categories ordinally. In Winsteps this is STKEEP=No.
To keep incidental unobserved categories, in Facets, it is "Keep". In Winsteps: STKEEP=Yes
SteveH:
[quote=ning]Hi Mike,
In your stacking approach, what if I end up with a set of threshold values that are disordered? Should I "fix" them and make sure they are ordered before I use them as anchor values in stage III?
Thanks.
Yes, you should fix 'them' or fix the problem that produces them.
The polytomous Rasch model requires ordered thresholds. The thresholds partition the latent continuum into contiguous regions. For example, if there are three categories you might have regions
----A----><---B----><-----C------
The locations >< are the thresholds, where it is equally likely that a person will respond in two categories; e.g. A or B. The score x = 0,1,2 is the number of thresholds in order exceeded by a person at a given location. Andrich (2005) shows in great detail that the score x summarizes a Guttman pattern at the (latent) thresholds. The score is the number of thresholds IN ORDER that are exceeded by a person:
0,0,0 <=> 0
1,0,0 <=> 1
1,1,0 <=> 2
1,1,1 <=> 3
where 0 and 1 denote that a threshold is not and is exceeded respectively.
The probabilities of these patterns have corresponding terms in the denominator of the polytomous Rasch model. The probabilities of non-Guttman patterns do NOT appear in the denominator. For example, there is no term corresponding with the pattern 0,1,0 as implied when thresholds are disordered. Disordered thresholds are clearly incompatible with the polytomous Rasch model (Andrich, 2005). You can keep them if you wish, but you're not using the Rasch model (and this is the same for the Partial Credit Model).
The *threshold* is a point between two regions. When threshold ESTIMATES are disordered, something is wrong. Above, threshold 1 lies between regions A and B, threshold 2 lies between regions B and C. Can you imagine how the continuum is partitioned into regions if they are disordered? It's not possible.
Good luck. There is a lot of confusion about the model, which is all explained in the following:
Andrich, D. (2005). The Rasch model explained. In Sivakumar Alagumalai, David D Durtis, and Njora Hungi (Eds.) Applied Rasch Measurement: A book of exemplars. Springer-Kluwer. Chapter 3, 308-328.
MikeLinacre:
SteveH writes: "The polytomous Rasch model requires ordered thresholds."
This is only true if one conceptualizes the categories as modal, i.e., each category in turn is more probable than any other category. But be sure to verify that the categories are ordered before being concerned about whether the Rasch-Andrich thresholds are ordered. See www.rasch.org/rmt/rmt131a.htm - "Category Disordering vs. Step (Threshold) Disordering"
If the conceptualization is ordinal (each category in turn is more of the latent variable) then disordered thresholds, but ordered categories, merely indicate that the category represents a narrow, but ordered, interval on the latent variable.
If the conceptualization of the categories is majority (each category in turn is more probable than all other categories combined) then thresholds must advance by more than 1 logit or so.
SteveH:
[quote=MikeLinacre]SteveH writes: "The polytomous Rasch model requires ordered thresholds."
This is only true if one conceptualizes the categories as modal, i.e., each category in turn is more probable than any other category. But be sure to verify that the categories are ordered before being concerned about whether the Rasch-Andrich thresholds are ordered. See www.rasch.org/rmt/rmt131a.htm - "Category Disordering vs. Step (Threshold) Disordering"
Actually, it's simply true. Andrich (2005) shows the reasons in detail.
Below Eq. (36) in Andrich (2005)
"It is important to note that the probability Pr{X_ni=x} arises from a probability of a relative success or failure at all thresholds. These successes and failures have the very special feature that the probabilities of successes at the first x successive thresholds are followed by the probabilities of failures at the remaining thresholds. The pattern of successes and failures are compatible once again with the Guttman structure. Thus the derivation in both directions results in a Guttman structure of responses at the thresholds as the implied response ...".
The connection between the (latent) Guttman structure and the model is made very explicit in this chapter and therefore if anything is wrong it should be possible to show precisely what is wrong.
Steve
MikeLinacre:
Thank you, Steve. It appears to be a choice of which axioms define a Rasch Rating Scale Model (RSM). Let's express RSM in terms of thresholds {Fk}:
Fk = Bn - Di - log (Pnik / Pni(k-1))
Then we can define three variants of RSM:
1. RSM(UC): Unconstrained: Fk can take any real value.
2. RSM(DC): Data-constrained: the data are manipulated until F(k-1) <= Fk <= F(k+1)
3. RSM(EC): Estimate-constrained: the threshold estimates are forced to comply with F(k-1) <= Fk <= F(k+1) but the data are not changed.
The Rasch axiom of "strict local independence" ("specific objectivity") supports 1. RSM(UC).
For 2. RSM(DC) and 3. RSM(EC), there is a different Guttman axiom of "constrained local independence".
Ben Wright advocates variant 1. RSM (UC).
David Andrich advocates variant 2. RSM(DC).
Some Rasch software implements variant 3. RSM(EC).
Does this correspond with your understanding?
SteveH:
[quote=MikeLinacre]Thank you, Steve. It appears to be a choice of which axioms define a Rasch Rating Scale Model (RSM). Let's express RSM in terms of thresholds {Fk}:
....
Does this correspond with your understanding?
Mike. No, it does not. Before I explain why, let me clarify your understanding of something.
Do you agree that Andrich (1978 ) first introduced the polytomous Rasch model, and that it has precisely the same structure as the Partial Credit Model, except that the threshold locations may vary across items in the latter? Do you agree that this paper was the first to resolve the category coefficient of Rasch's general model into a sum of thresholds (or whatever you wish to call them) and discrimination parameters, and to show that the discrimination parameters must be equal for sufficiency to hold.
Do you agree that Masters' (1982) derivation of the polytomous Rasch model from the dichotomous model leads to precisely the same model? That is, the only difference is that the specification of equal threshold distances from a central location in the model stated by Andrich (1978 ) is relaxed in the model stated by Masters (1982). If not, have you read Andrich (2005) or Luo (2005), in which this is clarified?
Do you agree that the distinguishing property of the models, in both forms, is the existence of sufficient statistics for the person and item parameters?
If you wouldn't mind, let me know the answers to these questions first, then I'll be happy to address your question about axioms directly and explicitly. I find people tend to talk at crossed-purposes about this issue and I'm never sure if people are genuinely familiar with Andrich (1978 ) and the subsequent papers showing the models are identical in the respects shown by Luo (2005).
Regards,
Steve
Andrich, D. (1978 ). A rating formulation for ordered response categories. Psychometrika, 43, 561-73.
Luo, G. (2005). The relationship between the Rating Scale and Partial Credit Models and the implication of disordered thresholds of the Rasch models for polytomous responses. Journal of Applied Measurement, 6, 443-55
MikeLinacre:
Thank you for your questions, Steve.
Surely we both agree with Erling Andersen, David Andrich, Geoff Masters, Ben Wright, ... that Rasch models are defined by the fact that they are logit-linear (or exponential) models which have sufficient statistics for all their parameters. Beyond this, as Jurgen Rost says, there is a "Growing Family of Rasch Models".
Each member of the family has its own parameterization, and other constraints or axioms, suited to its specific purpose. Some members of the family can be regarded as super-sets or special-cases of other members.
For instance, Huynh Huynh identified the conditions required for a Rasch polytomous item to be equivalent to a set of Rasch dichotomous items. This leads to a constrained version of the Rasch-Andrich Rating Scale model in which the threshold advance must be 1.4 logits or more.
Similarly, if a Rasch polytomous model is to be equivalent to a set of binomial trials, then the constraint on its thresholds is even stricter.
So, David Andrich is defining one member of the family by constraining the threshold ordering to "advancing in the data".
There is another member of the family in which that constraint is not imposed, as derived for instance by Gerhard Fischer in "Rasch Models, Foundations ...."
The confusion is that the two different family members are called by the same name. What names do you suggest so that we can distinguish between them?
846. Logit range -4 to 4???
jetera May 29th, 2008, 3:01am:
I am just learning about the Rasch model and I was wondering why there seems to be a consensus on the logit scale from -4 to 4. I can't find much on the internet that explains it so I appreciate any help!
Thanks in advance!
MikeLinacre:
Sorry, there is no consensus, jetera. The logit range depends on the randomness in your data. Experience is that most dichotomous data sets (True-False, Multiple-Choice) produce measures within the range -5 to +5 logits.
jetera:
Thanks! I couldn't find a solid answer anywhere and I am just learning :)
MikeLinacre:
Jetera, we are all "just learning"! We have barely scratched the surface of what there is to know about Rasch measurement.
847. collapse item
godislove May 14th, 2008, 11:53am:
Hi Mike,
is it possible to combine two items with the same difficulty measure and retest with Winsteps so that I can see the item distribution on the map?
Thanks in advance!
MikeLinacre:
How would you like to combine the items, godislove?
If they are dichotomies, scored 0-1, we could combine them into a 0-1-2 rating scale item. Is this what you want?
godislove:
Hi again,
sorry for not being so clear!
we would like to combine items that have the same difficulty measures since they measure more or less the same thing. We do not want to collapse categories in the rating scale. Is there a function in Winsteps that I can collapse two items to become one item? I know I can take away the redundant item in Winsteps by IDELETE= but I don't know which item I should remove since they have the same measures.
please advise!
MikeLinacre:
If the two items are the same item twice, godislove, then deleting one item is the correct action.
If the two items have the same difficulty, but are independent, then they are like two shots at a target. If we want to keep the two shots, but want them to count as one shot, we could use IWEIGHT= and weight each shot 0.5.
But in many situations, items with the same difficulty can be measuring different things. For instance, on an arithmetic test, a hard addition item and an easy division item can have the same logit difficulty measure.
Does this help?
848. Research and Rasch newbee looking for guidance
spthoennes May 9th, 2008, 6:12pm:
As a graduate student, I am a part of a group of researchers in the social sciences. I've been reading up on Rasch and it appears to be the best model for gathering data using the Likert scale and to measure attitudes between two groups toward one another before and after treatment. This is rather daunting to me, and I'm curious to know if I'm on the right track...TIA
MikeLinacre:
Sounds like the right track to me, Spthoennes. There have been many Rasch papers with pre- and post- designs. Google - Rasch pre post - to see a selection. Some are available online.
Forum members: any recommendations about good Rasch papers relating to this?
connert:
Hi and welcome to the board. I am a sociologist and former chair of my department. I have to say that the acceptance of Rasch techniques is minimal in social sciences. In my field there are not a lot of faculty who understand Rasch ideas. And there are a lot of faculty who still say "add up the rank labels and divide by the number of items" to get measurement. Don't succumb to that non-sense. It is a moral imperative to engage in best practice. Read Andrich's papers on resistance to Rasch measurement ideas. And think of yourself as a part of the vanguard of people who will reform measurement in social sciences. Hopefully we are near the tipping point. But every person counts.
spthoennes:
Thanks very much for the suggestions and encouragement. In case your interested, the research if for Laughter for Change, a group dedicated to using improv comedy as a means of healing the scars between tribes following the Rwanda genocide. I wish to measure inter-tribal attitude change following an improv comedy session by using pre- and post- Rasch analysis.
MikeLinacre:
A great application of Rasch analysis, Spthoennes! Will be very interested to read about your findings.
849. Counts Model
connert May 7th, 2008, 2:58pm:
I have telephone survey data in which a resondent is asked about a relative in long term care. In particular I have questions about frequency of incidents of kinds of abuse and neglect over the past year. For each type of abuse or neglect there are response categories of none, 1 or 2, 3 to 5, 6 to 10, more than 10. I have 1002 respondents. As you might expect the "none" category is selected a very high percentage of the time. My question is whether there is an appropriate Rasch model for this data. Does the high selection of one response category pose a problem for just doing an ordinary partial credit analysis?
MikeLinacre:
No particular problem, Connert. If this is a "normal" population, there are likely to be a lot of respondents with minimum extreme scores. There may also be very few observations (i.e., less than 10) at the top end of the rating scale for each item, so it may make more sense to combine the top two categories for some items. Trying the analysis with 5 categories and then 4 categories will indicate which works better. Do tell us how this works out.
850. Item Fit and DIF
Xaverie May 6th, 2008, 6:46pm:
I have a question about item fit and differential item functioning. All of my scale items have infit and outfit values between 0.7 and 1.3, which I interpret as meaning that they all fit the Rasch model well. However, when I checked for DIF, I found about half the questions functioned differently for men than for women. The easiest item for men to answer was the most difficult for women, etc.... My question is this. How is it that a scale item can fit well within the entire study population, but function so differently between men and women? Shouldn't I have seem poor fit on these items because the answers were so different between the sexes?
MikeLinacre:
A huge DIF size is surprising under these circumstances, Mudduck. The Rasch model predicts small random deviations. In DIF situations, these variations have piled up in one direction for one group and the other direction for another group. We only discover this when we segment the data by group. You may want to verify the DIF results. Analyze only the males (using PSELECT= in Winsteps) and then only the females. Cross-plot the two sets of item difficulties. The plot should match your DIF findings.
851. Startup of Winsteps
connert May 1st, 2008, 12:19am:
For some reason when I start Winsteps without it having been running since I last booted my computer and tell it I want to use an SPSS file it pauses while my system "configures" Amos 16.0. This is very annoying. Is there an explanation for this? I know that SPSS 16.0 is very buggy and that would be my first guess but I thought I would report it here.
MikeLinacre:
Thank you for this report, Connert.
This is a Windows problem. One possibility is that Winsteps is using a dll "dynamic link library" also used by SPSS/Amos. The configuration is flagged as not having completed, so Windows completes it, but doesn't turn off the flag.
If you are using Vista, please reboot, put yourself into Administrator mode (UAC), and then launch Winsteps. This may enable Windows to set the flags correctly. If that doesn't work, then reboot again, put yourself into Administrator mode (UAC) , and launch SPSS/Amos.
Reinstalling Winsteps is unlikely to solve this problem.
852. Large-scale FACETS analysis
SusanCheuvront March 27th, 2008, 3:58pm:
Hi Mike,
I've been running FACETS in pieces, just one analysis at a time while I learn the program. But now I want to run a full analysis. I have a CRT test scored by two independent raters. There are 60 items broken down into 5 levels with 12 items at each level. All items are scored 0 for incorrect and 1 for correct. I want to run an analysis that looks at the items, the raters and the levels, as well as the interactions among those variables. How might I set that up? I'm interested in overall rater agreement, as well as agreement at each of the 5 levels. I also need descriptive statistics for each item(item ease, point biserial etc.) I'm thinking:
1 = rater
2 = examinee
3 = levels (5 elements)
4 = items (60 elements)
Facets = 4
Models = ?, ?, ?, #, R12
Inter-rater = 1
Inter-rater = 3
1, 1, 3, 1-5, 8, 10, 7, 5, 6, 1-60, 1, 1, 1, 1, 0, 0....... Examinee 1 scored by rater 1 scores a 3 overall. At each of the 5 levels, examinee scored 8, 10, 7, 5, 6. Item 1 examinee got correct, item 2 correct, item 3 correct ...
MikeLinacre:
You are ambitious, Susan!
You wrote: "interested in overall rater agreement, as well as agreement at each of the 5 levels."
That requires two analyses, with two different data files.
Analysis 1. Overall agreement:
1 = rater
2 = examinee
3 = levels (5 elements) ; dummy facet: all elements anchored at 0
4 = items (60 elements)
Facets = 4
Inter-rater = 1
Gstats = yes ; computes the point-biserial
Models =
?, ?, ?, #, R12
?B, ?, ?B, #, R12 ; rater by level interactions
*
Analysis 2:
1 = rater
2 = examinee
3 = rater x levels (raters x 5 elements) ; dummy facet: all elements anchored at 0
4 = items (60 elements)
Facets = 4
Inter-rater = 3
Gstats = yes ; computes the point-biserial
Models =
?, ?, ?, #, R12
*
OK?
SusanCheuvront:
Thanks, Mike.
So, just to be sure, my data would look like:
Analysis 1
1,1,1-5,7,8,5,1,3,1-60,1,1,0...,4 Examinee 1 scored by rater 1 gets 7, 8, 5, 1,3 points at each level, gets item 1 correct, item 2 correct, item 3 incorrect... and scores a 4 overall.
Analysis 2
Would be the same, right?
Do I need to have 1-5 and 1-60 in the data line, or can the line just read:
1,1,7,8,4,1,3,1,1,0...4
MikeLinacre:
Thank you for asking, Susan.
There can only be one range per data line, and you have 12 items per level, so for level 3 (items 25-36), the data would be something like:
rater 4
examinee 17
level 3
items 25-36
observations: 1,0,1,0,0,0,1,1,1,1,1,1 (12 correct and incorrect responses)
Analysis 1:
4,17,3,25-36,1,0,1,0,0,0,1,1,1,1,1,1
Analysis 2:
for rater x level elements:
rater 1 level 1 = 1, rater n level m = (n-1)*5 + m
rater 4 x level 3 = (3x5) + 3 = 18
4,17,18,25-36,1,0,1,0,0,0,1,1,1,1,1,1
OK?
SusanCheuvront:
Hi Mike,
I'm totally lost. I thought I understood the difference between the two analyses, but now I'm not sure I do. They both look exactly the same to me. Facet 3 for the first analysis indicates that it's just levels, but under the models, it includes R12, then states "rater by level interactions." For the second analysis, facet 3 indicates a rater x level interaction, but the same R12 is in the model. If the first analysis isn't looking at agreement by levels, but the overall rater agreement, why is R12 in the model?
The second area where I'm confused is in what the data lines should look like. I don't understand what you mean when you say you can only have one range per data line. In your example, you have level 3(items 25-36). Forgive my stupid question, but what about the other items? Where do those go? And one additional question, in your example, the examinee got 8 items correct at that level. Does the data line have to include an 8 then?
In the second analysis, I'm not sure where the equation for the interaction term is coming from. I'm assuimg it's (level 3 x 5 levels) + 3, but what is the 3 that is added? Is that again referring to level 3?
Sorry to overwhelm you with questions!
Thanks
MikeLinacre:
It seems I didn't read your first post closely enough - so may have given you incorrect information, Susan. My apologies.
Looking at your data, it appears that it is scord 0 or 1. So the model should not be "R12" (a rating scale from 0 to 12) but "D", a dichotomy.
So the first model should have been:
Models = ?, ?, ?, #, D
The data is entered in the following format:
element number of facet 1, element number of facet 2, element number of facet 3, element number of facet 4, observation
This can be abbreviated if there is a range, but only one range is allowed, e.g.,
1,1,1,1-4, 0,1,0,1
1,1,2,5-7, 0,1,1
Please try this before attempting interactions.
SusanCheuvront:
Thanks, Mike,
Yes, the items are dichotomous, scored 0,1. So let me make sure I have this right. The example you just clarified for me would give me rater by level agreement, or overall rater agreement? How much data in one line can Facets deal with? Can I do one level (12 items) per data line?
So it would look like this:
1,1,1,1-12,1,1,1,1,0,0,0,1,1,1,1,1 ; Examinee 1, scored by later 1, at level 1 on items 1-12 scored....
1,1,2,13-24,1,1,1,1,.... Examinee 1, scored by rater 1, at level 2 on items 13-24 scored...
Do I have this right now?
Thanks!
Susan
MikeLinacre:
Yes, that looks correct, Susan. Well done!
If items are nested within level, then you have a decision to make.
A. Is the difficulty in the items? Levels are merely a classification. If so, "Level" is a dummy facet that should be anchored at 0.
Or
B. Is difficulty in the level, and the item difficulties are relative to the level difficulty? If so, the items need to be "group-anchored" at 0 within level.
SusanCheuvront:
The difficulty is a characteristic of the levels. Each level is incrementally more difficult than all levels below and the items in each level are very similar in that they all have similar difficulty. So, my guess is they would have to be anchored at 0 within each level, but I don't know what that means. Does this change the input at all?
Thanks!
Susan
MikeLinacre:
Thanks for the clarification, Susan.
You are more interested in the levels, than the items. This does not change the data layout, but it does change Labels=
Labels=
1, Examinees
...
*
2, Raters
...
*
3, Levels
....
*
4, Items, G ; group-anchor within level
1-12, Level 1 items, 0, 1 ; "0" means center the difficulty of the items at 0
; "1" this means this is group 1 of items
13-24, Level 2 items, 0, 2
.....
*
SusanCheuvront:
Thanks, Mike. I think that's clear. I'll let you know once I start trying to run the analysis! I have one last question. If I'm interested in rater agreement by level, can I include 'inter-rater = 3?' Will that give me what i want?
Thanks
Susan
MikeLinacre:
Does "rater agreement by level" mean "rater agreement within each level", Susan? If so, "inter-rater=3" won't work. You will need to analyze each level separately with "inter-rater=2" to obtain the wanted statistics.
To analyze a level separately, comment out the other level elements in the Labels= list.
SusanCheuvront:
Yes, I mean rater agreement within each level. When you say I have to comment out the other labels in order to analyze each level separately, what does that mean? How do I do that?
MikeLinacre:
Susan, in Facets, an easy way to omit elements from an analysis is to comment them out in the Labels= specification by prepending a ;.
For example:
Labels=
1,
....
*
3, Levels
1= level 1
; 2= level 2 ; this element is commented out, so its observations will be ignored.
...
*
SusanCheuvront:
thanks, Mike, but one more question. And I promise I'll never bother you again! ;D
To analyze each level separately, can you walk me through the input? I'm not sure what labels to comment out and, I would have to comment out part of the levels label, wouldn't I, since I'd be analyzing each level separately? How would I do that?
Thanks!
Susan
MikeLinacre:
Yes, Susan, to analyze a level, comment out the element labels for all the other levels. Remember that you are doing this so that you can investigate rater-agreement within levels. So specify
interrater = rater facet number
SusanCheuvront:
Okay, but can you please walk me through the exact input to do this?
Thanks
Susan
MikeLinacre:
Susan, sounds like you need to hire a Facets consultant, or take my online Facets Course starting this Friday, May 2, 2008, on www.statistics.com/ourcourses/facets
But let's see what we can do from where we are. Please email me your Facets specification and data file for as far as you have got.
853. comparing/estimating Rasch scores across samples
markusq April 17th, 2008, 4:03pm:
Hello,
I am still a little uncertain about my understanding of basic Rasch concepts, and about their role for my application problem.
The application is in sociology, a scale made of (only 5) rating scale items, administered to representative samples of 1,000-2,000 persons in a number of different countries. If the intention is to compare average person abilities across the countries, what is the ideal approach to estimate the measure(s) using Rasch analysis (and are there other maybe less optimal, but still viable ways?)
In classical test theory, with structural equation modeling, this would be the problem of scalar invariance of measures across independent samples.
I can think of two different approaches, each of which may be practically superior in a certain situation:
1. Test one Rasch model for a full, pooled sample, i.e. using all the data from all countries. Estimate person scores, compute average per country, ready. Common estimation takes care of common calibration, and all is well. Correct?
2. Establish that the 'same' Rasch model holds in each country sample. The questions here are: What makes a Rasch model sufficiently 'same' to allow for comparisons of average ability levels? Which role has specific objectivity here? Is 'sameness' already established by elementary DIF analysis, or are there more specific tests, which maybe also include multiple samples simultaneously (instead of just looking at pairs of samples)?
I guess that this will appear pretty basic to you, and therefore would be grateful if you could point me to accessible sources explaining this, and perhaps application examples similar to mine (PISA, on a more elaborate level?).
Thank you for your advice,
Markus
MikeLinacre:
Thank you for your question, Markus.
There are papers written on the problem of cross-country equating, but your approach looks practical:
1. Put all the data into one analysis. Report sub-total statistics by country.
2. Look for item x country DIF. This can be computed country vs. everyone instead of country vs. country.
"What makes an estimate sufficiently the same?" - This is the usual problem in DIF analysis. With your large samples, it is likely that almost all items will show statistically significant DIF. So the question becomes "What DIF is substantively significant?" Here you need to compare DIF size (divided by 5 to spread DIF effect across the test) with the differences between the countries.
If the DIF sizes are much smaller than the differences between the countries, then DIF is having no substantive impact, and can be ignored.
Otherwise, the problem is not a "Rasch" problem, rather it is a "latent variable" problem. Your items are testing different latent variables for different countries. You have to decide which items exhibit the intended latent variable for each country. In international studies, this can involve selecting only a meaningful subset of the items for the analysis for each country. For instance, omit the "snow" items for tropical countries.
markusq:
Mike, thanks for the quick and informative response.
Thinking about my problem a bit further, I notice that I should perhaps rephrase one part of my question, regarding the second approach of producing separate country estimates:
If DIF analysis shows no substantive difference between country specific Rasch models, why exactly is it then that I can conclude that the estimated person parameters can be compared across countries? In other words: which aspect or quality of the Rasch models 'proves' that the separately estimated latent variable values have the same metric, and the same zero point, even after the estimates come from different samples, and from separate estimation runs?
My vague understanding is that this must have to do with the items having been shown to be a valid instrument in all samples. The part which still escapes me is however why and how this proves that levels of the country tests can be compared? After all, there is no explicit common anchoring of the test in this process?
Again, I should of course mention that I should be happy to receive a pointer to a paper or book on this - I certainly would not want to make you explain beginners level stuff over and over again...
Thanks again,
Markus
MikeLinacre:
Thank you for your questions, Markusq. They are fundamental to any type of measurement. Imagine you were doing the same study of height in different countries, using tape measures. How would you verify that the measures of height were comparable?
One way would be to place the tape measures next to each other, and check that the numbers aligned.
We can do the same operation in Rasch. We place the item hierarchies next to each other and check that they align. This is what a DIF study of the pooled data (your 1.) is doing conceptually.
Or, in your 2, we would cross-plot the item difficulties and verify that they fall on an identity line through the origin. If they do not, we may have a "Fahrenheit-Celsius" situation, or we may have incomparable measures (such as height and weight).
"Applying the Rasch Model" by Bond & Fox is a good introductory textbook to Rasch.
markusq:
Mike, thanks again.
With your help, I am getting closer to the core of my problem step by step :) .
(I had in fact read most of Bond & Fox already - and I like the book, - but somehow I still don't get the point. Please see below.)
Taking up on your example of tape measures, I return to the zero point problem. If I understand this correctly, Rasch person and item parameters are difference scaled, not metric. This means that the zero point is specific to each of our different tape measures. What I can easily proof by holding them against each other is that the ticks on each tape have the same distance, i.e. it is no problem to establish a common metric by DIF analysis (again using SEM terms).
BUT: It seems to me that your example is also tacitly assuming that both tape measures are held to a common starting point, e.g. ground level. This ground level however is not a property of the individual tape measures themselves, it is an external fact - external to all tape measures.
The same confuses me about Rasch estimates from different samples. In a purely technical sense, item difficulties estimated from a specific sample derive their zero point from that actual sample, and from nowhwere else. Then, person parameters for that sample are derived in relation to that (arbitrary?) zero point. Then how can I assume or show that the item difficulty zero points (and consequently, the person parameter zero points) are the same across independent Rasch models? How do I get at the common ground level?
Going back to the DIF analysis (which I, as a beginner, always imagine in the simplest fashion of only two samples, plotting item difficulties from one sample against item difficulties against the other sample): If I take zero points/origins for each series as given, I have no problem with that. What we are happy with is when we get a 45° line through the origin. Bingo, no DIF, same levels.
However, to me the property of 'difference scaling' means that one can add or substract an arbitrary constant from each estimated scale, without changing its meaning at all. This moves the DIF line horizontally or vertically in the coordinate system, but of course maintains the slope. Is this shifting of levels not a problem? Why not?
This is why I referred to specific objectivity in my original post. I have a feeling that the answer to my problem is hidden there? Somehow Rasch models use arbitrary zero points, yet manage to establish the same arbitrary zero points across independent samples. Is there a good explanation of this 'somehow'? Which pages of Bond & Fox should I re-read a few times to get it?
Thanks again,
Markus
markusq:
Mike,
A quick amendment: I think I am asking about how to deal with the "Fahrenheit-Celsius" situation which you mention. This example is close to my thinking: different arbitrary zero points, and different 'surface' metric, but of course the same underlying construct. Is this not very likely to happen with independent samples? Simple graphical DIF analysis then checks for identity of intervals, i.e. the 'surface metric', but I am missing where it validly addresses the question of common origins.
Markus
MikeLinacre:
The problem of "zero points" - local origins - arises also in bathroom scales, Markus. Weigh yourself on someone else's bathroom scale and you will soon discover that their zero calibration is different from your own bathroom scale!
In Rasch measurement, we would like a context-independent zero point, but that is as difficult to obtain as "sea-level" for measuring mountains. The only way we can do it it by imposing some theory about the placement of the zero point. In tape measures, the zero-point is "at the end". For steel rulers, it is "almost at the end". For Rasch measures the local origin is defined to be at the average of the current set of item difficulties. This makes it as person sample-independent as possible.
Of course, different sets of items will have different zero points, and different person samples may introduce DIF which will also cause movement of the zero point. So, when necessary, we engage in elaborate equating procedures. A physical equivalent would be to equate the "sea-level" for Mt. Everest to the "sea-level" for Mt. McKinley.
markusq:
Mike, thank you very much - this actually settles my problem, as I understand it to say this: no proof about same levels without an explicit equating exercise, which MUST involve testing (a selection) of overlapping items, on (a selection of) overlapping persons.
Still, the advantage of Rasch is that the assumption about a common set of items (with the same parameters) having the same average zero-point across independent samples is at least pretty plausible in many settings. Is this a correct way to put it?
MikeLinacre:
Yes, Markus. Plausibility and utility are what decide many things in life for us. Rarely do we have the capability to construct definitive proof.
Overlapping items ("common item equating") and overlapping persons ("common person equating") are two equating methods, but there are others, www.winsteps.com/winman/equating.htm
tgbond007:
Dear Markus, If you look at ::)everybody's favourite Rasch book ::) p186 you can see reference to the technique of setting the 0 origin at the mean of the sample ability (rather than the mean of item difficulty) gives some sub-sample v whole sample contrasts. The original paper series in JAM gives more detail...
markusq:
Thanks for the hint. I first guessed that famous & favourite book would be the same one as was recommended above? :-)
However, my copy (edition of 2001) has nothing about setting origins on p 186 or around, so it must be something else?
Thanks, Markus
tgbond007:
Goodness me Markus, surely you'd love to have a later copy of said ;Djewel ;D. But never mind, you can follow up on p142 with the old technology :D
854. Rasch Calibration on UNIX
wongcc April 25th, 2008, 2:05am:
Hi,
Does anyone knows of any software that could calibrate Master's Partial Credit Model on a UNIX platform? Some needs are:
- runs on UNIX
- can calibrate polytomous items
- the software should be able to generate output files containing person and item parameters, as post-processing using SAS is needed.
Any clue or sharing of experience would be of great help to me.
I found 'Conquest' but is not sure if it runs on UNIX.
Thanks and regards
Cheow Cher
MikeLinacre:
Thank you for your question, Wongcc.
All the Rasch software I know about is listed at www.winsteps.com/rasch.htm
855. expressions
jingjing1 April 18th, 2008, 3:34am:
I use the Many Facets Rasch model(Facets), but I don't konw the expressions of the judge's reliability(not inter-rater), so I can't understand the result of the table 7.1.1.
Will sb tell me the expressions? :)
MikeLinacre:
Thank you for your question, Jingjing1.
Most reliabilities reported by Facets are the reliability of differences, similar to Cronbach Alpha, KR-20, etc. They report:
Reliability = True variance / Observed variance.
where True variance = Observed variance - Error variance.
In Rasch computations, we know the observed variance, and can estimate the error variance from the measure standard errors. For more details, see www.winsteps.com/facetman/table7summarystatistics.htm which is also in Facets Help.
jingjing1:
Thank you very much for your reply,Mike.
I am a China girl,and a post graduate student for grade one.my major is psychology about Stat. and measurement.This is one part of my paper,Thanks for your help,if i need your help again ,keep in touch ok?
jingjing1:
Hello, Mike,
I did a reasch, and want to know the every dimension's reliability. there are two tables, Table 7.1.1 rater Measurement Report and Table 7.2.1 examinee Measurement Report, Table 7.1.1's Reliability (not inter-rater) is 0.22,Table 7.2.1's Reliability is 0.89.
I want to know the difference between them, and if I want to report the reliability of every dimension, which one should be reported in my paper?
MikeLinacre:
Thank you for your question, jingjing1.
Since the purpose of most tests is to measure the examinees reliably differently (= reproducibly differently), then it is the reliability of the person sample that is reported. In your analysis, Facet 2 is the examinees, so Table 7.2.1 reports their measures, and the reliability of that sample of measures = 0.89.
We usually prefer that the raters not be reliably different in leniency, so your low rater reliability of 0.22 is welcome. This is not the same as an inter-rater reliability coefficient which reports whether raters are reliably the same (not different), and we usually want inter-rater reliability to be high for raters.
jingjing1:
Thanks Mike,it is so gratitude,i learn more from your reply,and i will go on doing this,thank you very much.
in Facets Help,i found that separation reliability (not inter-rater)in Table 7.2.1 is low(near 0.0)judge and rater reliability are preferred,
so if separation reliability (not inter-rater)=0.98,it means raters are reliably the same ,and not be welcome it is right?
MikeLinacre:
Jingjing1, if your raters are reliably not the same, then they definitely do not have the same severity or leniency. This is the reason we use a Facets model, because the Facets model adjusts for differences in severity and leniency. Traditional analysis of raters does not.
Unwelcome raters are those who vary their severity or leniency. These are unpredictable raters, and so will have noisy fit statistics.
jingjing1:
Thanks Mike.
i see.
I wrote it mistakenly ,and this time i know your mean .Thank you again.
jingjing1:
Thanks Mike.
i see.
I wrote it mistakenly ,and this time i know your mean .Thank you again.
856. Facets output interpretation
Michelangelo April 21st, 2008, 3:48pm:
Hi all :)
I don't understand how to interpret the "bias term" and the "target contrast" provided respectively in tables 13.1.2 (Bias/Interaction Calibration Report) and 14.1.1 (Bias/Interaction Pairwise Report).
Please let me describe the analysis I'm running.
Data comes from a lexical decision task. In a computerized procedure participants have to categorize stimuli in their categories as quickly as possible (e.g. tulip goes in the category "flowers" and fly goes in the category "insects"). Discretized latencies constitute the dependent variable (three levels: fast -coded 3-, medium -coded 2-, and slow -coded 1-).
This lexical decisions are provided in two different conditions (within subj): let's call them "red" and "green" conditions.
I want to know if tulip is categorized faster in the red or in the green condition, so I run a bias analysis between the facets "items" and "conditions". So I get (at least) two tables: the calibration report and the pairwise report. According to Facets manual, they provide the same information, but this is not my experience. Looking at the the calibration table, I get these lines:
Obsvd Bias Model
Score Measure S.E. Cond measr Items measr
186 -.19 .14 red -.61 tulip -.42
234 .15 .13 green .61 tulip -.42
From this table, I understand that tulip was identified faster in the green condition, since here it gathered more quick responses (obs score= 234).
On the other side, if I look at the pairwise table I get these lines:
Context Target Context Target Target Joint Target
Cond measr Cond measr Contrast S.E. t Items
green -.57 red -.23 -.34 .19 -1.74 tulip
From this table, I understand that tulip have a logit of -.57 in the green condition and one of -.23 in the red condition. I asked for all positive facets, so I conclude that tulip is easier in the red condition (in this condition its logit is higher: -.23 > -.57). The opposite of what I conclude looking at the previous table.
I discovered that the sum of the two bias measures provided in table 13.2.1 gives the target contrast provided in table 14.1.1 but this doesn't help...
I would really appreciate if someone could help me in getting where I'm wrong.
Thanks,
Michelangelo
MikeLinacre:
Thank you for emailing me the Facets specification and data files, Michelangelo.
Target means "apply the bias to the measure of this element"
Context means "the bias observed when the target element interacts with the context element"
In Facets 3.53 the signs in your first table are "higher score=lower measure". This was the default: Bias = Difficulty.
Here is the same table when "higher score = higher measure". To obtain this, please specify:
Bias = Ability
Obsvd Exp. Bias Model
Score Score Measure S.E. Cond measr Items measr
186 177 .19 .14 red -.61 tulip -.42
234 243 -.15 .13 green .61 tulip -.42
This is the correct computation:
Bias | target = tulip
Measure Cond measr Items measr | bias overall context
0.19 red -.61 tulip -.42 | .19 + -.42 = -.23 relative to red
-.15 green .61 tulip -.42 | -.15 + -.42 = -.57 relative to green
Michelangelo:
Thanks for your quick and effective help, Mike.
Now it's clear.
M.
857. RASCH and Stage Models
pjiman1 April 18th, 2008, 5:32pm:
5. I wonder how RASCH can be applied to scales that have stages that according to the developers, people can revisit earlier stages. For example, in Prochaska and DiClemente stages of change questionnaire, there are pre-contemplative, contemplative, preparation, action, and maintenance stages and participants progress through those stages in that order. It is possible for participants to be in an later stage, only to be later have a relapse and get classified in an earlier stage. Similarly, in gay/lesbian self-identity models, authors have stated that people can be in later stages of identifying as a gay or a lesbian, but they could also revisit earlier stages as they gain clarity on their overall identity. These types of stage models of development where people can revisit earlier stages do not seem to lend itself to a RASCH model. It would seem that once you have reached an advanced stage, you stay there because in the RASCH model, you are expected to “accomplish� the earlier stages. However, the scales constructed to assess these models all assume linear progression. Upon scrutiny, it would seem that the authors would have to provide a rationale for why a person would revert back to earlier stages. In the stages of change example, the reason why a person would revert back to earlier stages might be because the person no longer has the ability to maintain his/her progress at the later stages. In the gay/lesbian identity model, the reason why a person would revert back to earlier stages is because the person has a better understanding of his/her own identity and wants to gain better clarity. It is my impression that in designing the scale items that it would be necessary to acknowledge why a person would revert back to earlier stages. I am having trouble reconciling how these types of stage models and their accompanying measurements would conform to a RASCH model.
Thanks,
Peter Ji
MikeLinacre:
There are several approaches to regression to earlier stages, pjman1. The first challenge is to verify that it is actually happening in your data. Suppose we were doing the same thing investigating a weight-loss program. We would measure an individual's weight at different time-points. Then plot the measures to see the what is happening. Some people would lose weight. Some would gain weight. Some would oscillate. But that does not alter the functioning of the measurement instrument. We can do exactly the same with Rasch measurement. The characteristics of the questionnaire should not alter depending on whether the respondent is progressing or regressing along the latent variable. But, if the characteristics do change, Rasch analysis will identify where and in what way they are changing.
tgbond007:
While many developmental models are cumulative (e.g. they are the focus of several chapters in B&F), some allow for regression (e.g., Freud's thumb-sucking adults). But the ruler you need in order to measure such development - and regressions - is the same one: the ruler remains fixed (calibrated) the people grow and regress in relation to it.
858. person outfit - treat as outliers?
pjiman1 April 18th, 2008, 5:29pm:
1. I have a question about person outfits and infits. If the infit and outfit statistic is too high for a given person. According to Bond and Fox, (p. 40) if a person’s performance is not conforming to the expected item ordering, “something else is contributing to the person’s score.� If so, would this person be considered an outlier in the classical test theory sense? The person’s score is not expected and is probably an indication that another type of scale is needed to assess the person’s ability. To borrow a pop culture example, Dustin Hoffman’s character in the movie “RainMan� could get a complex square root problem correct without the aid of a calculator, but cannot do simple adding and subtracting. On a standard math scale, this character would yield a high outfit and some other scale would have to be used to assess his math performance. If so, should that person be considered an outlier and dropped from the sample and not used in future analyses? Is the infit or the outfit statistic more appropriate for detecting these person “outliers?�
Thank you
Peter Ji
MikeLinacre:
Dustin Hoffman would definitely be "off-dimension". Classical Test Theory does not usually investigate person fit, but, if he was an item, he would probably have an unacceptably low point-biserial correlation.
If you are looking for conspicuous off-dimension behavior (such as guessing, carelessness, etc.) then Outfit statistics are the ones you want.
You can omit grossly mis-performing persons while investigating item functioning. Then anchor the items at their "good" difficulty measures, and reinstate the entire sample for the final reporting.
tgbond007:
I presume that the Rain Man will have a low total score on the test but will, quite unexpectedly, get the easy ones wrong and harder ones right!! This will give him a low ability estimate (due to low total score) but large person misfit (esp. the OUTFIT indicators) because most of his responses were not predictable: from a low score we predict easy ones right and harder ones wrong - but Rain Man goes against all our expectations. Putting such misfitting persons aside while you investigate the the item stats is a good idea.
859. clarifying bias terminology
harmony April 21st, 2008, 4:25am:
Hello everyone:
I would like to clarify the difference in meaning between absolute measures, average measures, and relative measures to assist more accurate and informative reading of bias interaction plots in Excel. Any help is appreciated. :)
MikeLinacre:
Thank you, Harmony.
"Absolute Measures" are measures relative to the local origin on the latent variable, usually the average difficulty of the items.
"Relative Measures" are measures relative to the estimated overall difficulty of the item (or ability of the person).
"Average measures" are the average of a set of measures. What is averaged depends on the context. For instance, it could be the teh average measures of all the persons who are observed in a particular category of an item.
860. 'examinee' misfit in FACETS
ImogeneR April 18th, 2008, 5:22am:
Hi,
I'm posting this query here as others may have a similar issue.
I've been conducting rater/examinee/score analysis in FACETS for test that acts like an OSCE assessment in medical education (ie examinees rotate through 8 different stations so they see 8 different examiners, then their total is summed.)
IN a partial credit analysis we find that the 'item' facet fits well, we have a small number of misfitting judges (with a fairly broad range of severity and leniency) and a small number of our examinees underfit and overfit the model. For each measure of item ability there is a range of raw scores (showing that raw score did depend on which judges you saw).
So we would now say that we should use the Rasch measures as the 'true' score.
However, this is a high stakes test and before we could convince any Faculty committee to trust that notion (against their own scoring judgment, sort of) I need to be sure I've covered a few issues I'm still struggling with conceptually.
Are the following steps reasonable do you think in assessing the data
1) If I take the candidate with the largest example of misfit (~2.34 and a bit of an outlier ) , and then look at the fit of the judges who assessed this candidate and the fit of the items they were asked to rule out any 'test' source of over-randomness as opposed to intra-examinee randomness? IN this case the judges were all of good fit as were the items , the candidate got very low scores on about 3 of the items and high scores on the others, and there was no indication form judge leniency or item difficulty that suggested this pattern. So do we just assume then the misfit is candidate behaviour and would use the rasch ability level for this candidate? What would happen if we found that the judges this examinee saw showed significant misfit - could we still give that examinee their rasch measure in the test (which is used for ranking)? Or could this be challenged?
Do MFRM analysis where examinee measures are used for decision meaking, either pass/fail or selection get scrutinised at this level?
Many thanks,
Imogene
MikeLinacre:
Thank you for your questions, Imogene. An unexpected response will cause misfit in all elements that participated in generating the response (candidate, item, judge, ...). So it is the accumulation of unexpectedness that guides our thinking. If a candidate is involved in a lot of unexpected responses, the candidate will misfit. Similarly for a judge or an item.
Rasch is reporting on the data. The inconsistent response patterns are in the data. Rasch didn't cause them. Rasch merely discovered them. So if the Rasch measures are dubious, then the raw scores are even more dubious.
An approach is to comment-out suspect ratings and see what impact they have on the decisions. Imagine you are the lawyer for the candidate - what would be the impact of removing the judge? Frequently you will discover the impact of the misfit has no substantive impact. If it does, then which is more reasonable, the measure with the judge or the measure without the judge (or whatever)?
861. Primer on Item anchoring and item stacking
pjiman1 April 18th, 2008, 5:30pm:
Do you have a good primer on the item anchoring and item stacking RASCH procedures and interpretation of the output?
Peter Ji
MikeLinacre:
You are asking a lot, Peter! There is the introductory book, "Applying the Rasch Model" by Bond & Fox. Then there are numerous Rasch Courses, workshops and publications. The mechanics of anchoring and stacking depend on the software that is being used. The interpretation of the output is basically the same as with all other Rasch analyses, except that we would be particularly interested in "displacements" with anchoring, and, for stacking, the cross-plotting of measures for the same person in different parts of the stack.
862. Mixing Causal and Effect Indicators in a RASCH mod
pjiman1 April 18th, 2008, 5:30pm:
I read an article by Lennox and Bollen about causal and effect indicators in a factor model. Briefly, causal indicators are those variables where a one-unit increase in any one of those variables will lead to a corresponding increase in their associated latent variable. For example, if the causal indicators are “I can’t get up in the morning�, “I have no appetite�, “I have no friends�, “I lost interest in my hobbies�, a one unit increase in any one of those variables will lead to a corresponding increase in the latent variable – depression. Effect indicators are those variables where a one-unit increase in the latent variable will lead to a corresponding increase in all of the variables that are associated with the latent variable. For example, if the latent variable is depression, a one unit increase in the latent variable will lead to a corresponding increase in the following effect indicators: “I feel down�, “I feel sad�, “I feel blue�, “I feel depressed.� The article argues that because of these two types of indicators, conventional rules of thumb for evaluating the fit of these models do not hold. Problems arise when evaluating a factor model if a latent variable consists of a mix of causal and effect indicators. My question is does RASCH ignore the type of item in its analysis? In other words, can causal and effect indicators be mixed together and RASCH will analyze the items in the same fashion?
Peter Ji
MikeLinacre:
Rasch conceptualizes the latent variable in terms of qualitative indicators, pjiman1. So you submit the data collected on the indicators to Rasch analysis, and the analysis will report how coherently they indicate one dimension. If causal and effect indicators are different statistical dimensions, then Rasch analysis will reveal that fact. The "rules of thumb" for fit are somewhat incidental here, just as they would be if one mixed "reading" and "arithmetic" items on the same educational test. We would expect to see a general upward trend on the combined educational test with increasing grade-level, but inspection of the Rasch results would quickly reveal that we are attempting to measure two different things at the same time. Unfortunately analysts are often not informed of the content of the items, and so are forced to fall back on "rules of thumb" in situations like this.
863. RASCH Model Applied to constructs that Fluctuate
pjiman1 April 18th, 2008, 5:31pm:
4. I am curious on your views of constructs that fluctuate over time. In physical measurement, an entity can go up or down. Temperature varies from one day to the next. Or, a quarterback will throw for 250 yards in one game, 100 yards in the next game. According to RASCH model, if the underlying assumption is the ability to answer an item correctly, it would seem that this ability is fixed and no matter the conditions or context, it is safe to assume that a respondent with a specified level of ability will always get a set of items correct. Does RASCH account for the fact that sometimes there are phenomenons that are meant to fluctuate over time? For example, in the psychology/counseling literature, the phenomenon of the working alliance is such that in successful therapy experiences, the working alliance starts strong in the initial stages of therapy, will tend to decrease in quality in the middle stages of therapy (the working through stages), and rebound back to its initial stage of strength in the latter stages of therapy. Here we have a phenomenon that is meant to fluctuate. The measure for this phenomenon is the working alliance inventory and it has been used in hundreds of papers. To my knowledge, it has not yet been subject to a RASCH analysis and I am wonder how RASCH can be applied in an analysis for something that fluctuates each time it is measured.
Peter Ji
MikeLinacre:
Rasch analysis construct measuring instruments, pjiman1. We usually hope that our subjects will change on them. For instance, we measure the "quality of life" of medical patients during rehabilitation. We definitely want that to improve, but sometimes it doesn't. The effectiveness of the measuring instrument is independent of the status of the patient.
864. Likert Scale Issues
pjiman1 April 18th, 2008, 5:33pm:
6. I have concerns about likert scales.
a. Given that some items have likert scales that participants are able to discriminate between all of the categories and some items have categories where participants did not use all of the categories in an orderly fashion, is it permissible for a scale to have items with different number of categories? For example, if some items work better with a three point scale and some items work better with a four point scale, is it okay to have such a scale? Too often I see scales where it seems that for convenience sake, all items have the same number of categories.
b. During scale development, I have seen the same item but with different types of likert scale categories. For example, the same item can have a 5-item agreement scale - Strongly Disagree, Disagree, Neither Disagree nor Agree, Agree, Strongly Agree and a 4-item frequency scale – never, a few times, some times, many times. Is there any type of procedure that could be used to establish the equivalency of these items and their different types of likert scales? I am aware of item equivalency and item banking procedures, but those practices are applied to items with similar content and the same rating scale. What happens if the rating scale is fundamentally different for the same item?
c. Similar issue, I have seen scale items administered using a 5-point opinion scale and a 4 point opinion scale. For example, the 5 point would be Strongly Disagree, Disagree, Neither Disagree nor Agree, Agree, Strongly Agree. The 4 point scale would be Strongly Disagree, Disagree, Agree, Strongly agree. The problem is determining if the 5-point and 4-point scale demonstrates any equivalency. A concern I have is that there is no corresponding neutral category from the 5 point scale that could easily be compared with a category in the 4 point scale. Is there any way RASCH could help me determine if these 5- and 4-point likert scales demonstrate any equivalency?
Thanks,
Peter Ji
MikeLinacre:
Thank you for your question, pjiman1.
6a. Different number of categories is fine. Either use the "partial credit' model where each item is modeled to be different in some way, or apply an Andrich rating scale model to groups of items with the same number of categories.
6b. Under Rasch conditions, each one category advance up a rating scale is conceptualized to be an advance of one qualitative level of unknown size quantitatively. The Rasch analysis reports the size of the quantitative advance, and whether it makes sense qualitatively in the overall context of all the items and categories.
"rating scale is fundamentally different for the same item" - if the rating scale is defined differently, then the item becomes a different item. A typical example of this is when "frequency" and "importance" rating scales are attached to the same item stem. "Brushing your teeth? How often? How important?"
6c. Investigations of rating-scale-categorizations are usual in Rasch rating-scale analyses. In your example, here's an immediate question; "Is 'Neither Disagree nor Agree' on the same dimension as the other Likert questions, or is an off-dimension category indicating 'I don't want to answer this question.'" If it is on-dimension, then we have a 5-category (more discriminating) rating scale to compare with a 4-category (less discriminating) rating scale. Rasch fit statistics would indicate which of the categorizations fits better with the categorization of the other items.
865. Table 28
petrasseika March 21st, 2008, 9:18am:
Hello, has anybody used table 28 to analyse rating scale data?
I hame met one problem, i am analysing person responses twice and i want to compare answers after period of 48 weeks. It means that same persons takes same test twice in period of 48 weeks where they gives answers to 21 question, responses are 0 - Never/No , ... , 5 - Always/Yes. there are 5 groups or persons i want to compare and evaluate which group made a biggest progress (persorns are suffering heart from diceases). Then i see:
PERSON RELIABILITY .00 |
PERSON RELIABILITY .00 |
Does it mean that information is useless, that i should not trust it?
Also may it be that the reliability is different for the same person group, i mean it looks interesting when person reliability for group is 0.80 and after 48 weeks it becomes 0.20?
It would be wonderful if someone tell me what are the most important points in table 28.
MikeLinacre:
Person reliability is an indication of how reproducible the measurement order of the persons in your sample is expected to be statistically, Petrasseika.
A reliability of .00 means that all the observable difference in your person measures could be caused only be measurement error, not by substantive differences in performance on the latent variable.
So person reliability of .00 means that inferences made on measurement ordering within groups is not to be trusted. But you are investigating measurement ordering between groups. These reliabilities say nothing about that.
For example:
Group A. Time point 1. All score 1. Person reliability at time-point 1 = .00.
Group A. Time point 2. All score 4. Person reliability at time-point 2 = .00
Change from Time point 1 to Time point 2, substantively huge and highly statistically significant.
harmony:
One other possibility is that you may have forgotten to input the answer key.
866. Item-trait DIF in RUMM and WS
henrikalb April 16th, 2008, 4:37am:
Dear Mike,
According to ”A User's Guide to W I N S T E P S”, p.253 the values in Table 30.4 are equivalent to the item-trait chi-square statistics reported by RUMM.
After removing 90 out of 118 polytomous(4-levels) items from a dataset I get for the item-trait statistics with 10 stratae (DIF=MA10) in
RUMM: Total_chi_square = 525,561; DF = 252; p = 2,12752E-21
WINSTEPS: Total_chi_square = 178,4149; DF = 198; p = 0,837653
Is it expected to have this big a discrepancy between the two programs?
RUMM seems to always use the same number of stratae for all items.
Sincerely yours,
Henrik
MikeLinacre:
Thank you for your question, Henrik.
RUMM and Winsteps compute strata differently. With large sample sizes and reasonable measurement ranges their results are usually equivalent. This conforms with the scientific principle that reasonable alternative methods of obtaining the same finding should report the same finding.
You have 10 strata and 28 items. So there are 280 strata - 28 items = 252 d.f. as RUMM reports. RUMM takes the person sample and stratifies it into 10 sub-samples of approximately equal size. So RUMM almost always finds 10 strata in any sample of more than 10 persons.
Winsteps takes the sample measure range and stratifies it into 10 equal measurement intervals. In this case, Winsteps reports 198 d.f., so 252-198 = 54 Winsteps measurement strata do not contain any members of the sample.
This suggests that either your sample distribution has gaps in it, or your sample is too small for a robust stratification into 10 levels.
Which chi-square p-value is more reasonable? The RUMM result suggests that the data noticeably misfit the Rasch model. The Winsteps result suggests that the data exhibit good fit to the Rasch model.
In Winsteps, look at the dispersion of the item OUTFIT MNSQ statistics. Is it small (e.g., S.D. = 0.2) supporting Winsteps, or large, (e.g. S.D. = 0.5) supporting RUMM?
Please do tell us what you find .....
henrikalb:
Dear Mike,
According to table 3.1 (please see below, sorry I was unable to format it with Courier font)
S.D. OUTFIT MNSQ = 0.57, so I suppose S.D. is big.
I also tried with DIF=MA3 with 78 out of 118 items and got
RUMM: Total_chi_square = 657.827; DF = 156; p = 8.38235E-63
WINSTEPS: Total_chi_square = 120.3094; DF = 136; p = 0.8288954
so there seems to be a big difference between RUMM and WINSTEPS.
Is it possible to make WINSTEPS behave like RUMM?
Sincerely yours,
Henrik
TABLE 3.1
INPUT: 10524 Persons 118 Items MEASURED: 10419 Persons 28 Items 4 CATS 3.64.2
--------------------------------------------------------------------------------
SUMMARY OF 9394 MEASURED (NON-EXTREME) Persons
+-----------------------------------------------------------------------------+
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 12.3 5.0 -.04 .61 .93 -.1 .93 -.1 |
| S.D. 5.7 2.6 .99 .19 .57 1.2 .57 1.2 |
| MAX. 74.0 28.0 3.02 1.13 3.18 4.3 3.46 4.5 |
| MIN. 2.0 1.0 -3.95 .21 .00 -5.3 .00 -5.3 |
|-----------------------------------------------------------------------------|
| REAL RMSE .69 ADJ.SD .72 SEPARATION 1.04 Person RELIABILITY .52 |
|MODEL RMSE .64 ADJ.SD .76 SEPARATION 1.19 Person RELIABILITY .59 |
| S.E. OF Person MEAN = .01 |
+-----------------------------------------------------------------------------+
MAXIMUM EXTREME SCORE: 816 Persons
MINIMUM EXTREME SCORE: 209 Persons
LACKING RESPONSES: 105 Persons
VALID RESPONSES: 17.9%
SUMMARY OF 10419 MEASURED (EXTREME AND NON-EXTREME) Persons
+-----------------------------------------------------------------------------+
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 12.0 4.8 .12 .73 |
| S.D. 5.8 2.6 1.30 .41 |
| MAX. 100.0 28.0 5.25 1.87 |
| MIN. 1.0 1.0 -5.27 .21 |
|-----------------------------------------------------------------------------|
| REAL RMSE .87 ADJ.SD .97 SEPARATION 1.11 Person RELIABILITY .55 |
|MODEL RMSE .84 ADJ.SD 1.00 SEPARATION 1.19 Person RELIABILITY .59 |
| S.E. OF Person MEAN = .01 |
+-----------------------------------------------------------------------------+
Person RAW SCORE-TO-MEASURE CORRELATION = .26 (approximate due to missing data)
CRONBACH ALPHA (KR-20) Person RAW SCORE RELIABILITY = .00 (approximate due to missing data)
SUMMARY OF 28 MEASURED (NON-EXTREME) Items
+-----------------------------------------------------------------------------+
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 4116.1 1680.6 .00 .06 .98 -.3 .97 -.4 |
| S.D. 5128.5 2091.4 .34 .03 .07 1.2 .08 1.1 |
| MAX. 15999.0 6505.0 .70 .13 1.18 2.2 1.26 1.8 |
| MIN. 205.0 82.0 -.79 .01 .76 -2.7 .72 -2.5 |
|-----------------------------------------------------------------------------|
| REAL RMSE .07 ADJ.SD .33 SEPARATION 5.09 Item RELIABILITY .96 |
|MODEL RMSE .06 ADJ.SD .33 SEPARATION 5.14 Item RELIABILITY .96 |
| S.E. OF Item MEAN = .07 |
+-----------------------------------------------------------------------------+
DELETED: 90 Items
UMEAN=.000 USCALE=1.000
Item RAW SCORE-TO-MEASURE CORRELATION = -.27 (approximate due to missing data)
47057 DATA POINTS. APPROXIMATE LOG-LIKELIHOOD CHI-SQUARE: 105481.71
MikeLinacre:
Thank you, Hendrik. The relevant statistics are shown in red. These seem to agree more with the Winsteps finding than the RUMM finding. But this may not be the whole story .....
To exactly duplicate the RUMM computation, you need to add a new indicator variable to the Winsteps person label. Here's how:
1. Output the Winsteps PFILE to Excel.
2. Sort on Measure.
3. In a blank Excel column, put a "0" for the first tenth of the sample, "1" for the second tenth etc. to "9" for the last tenth. RUMM does not allow the same measure to split between tenths, so if the end of a tenth will split a same-measure-group put all the same-measures into the same tenth, that of the majority.
4. Sort on entry number
You now have a column of tenth indicators.
You need to "rectangular copy" this into your Winsteps person labels. I use TextPad or Word. Here is a way using Excel:
5. Copy your Winsteps data file into another Excel worksheet.
6. Text to columns: split the person label from the data.
7. Insert a blank column before the person labels.
8. Paste in the column of tenth indicators.
9. Copy and paste the worksheet into a text file
10. Replace "tabs" with 'blanks" (do this by highlighting a tab and then "copy" into the Replace dialog)
11. This is your new Winsteps data file.
12. Adjust the Winsteps control file, so that the person NAME1= is the tenth indicator column.
13. DIF Table 23 with $S1W1.
MikeLinacre:
Another thought, Hendrik. About 82% of your data are shown as missing. Please check that RUMM and Winsteps are treating missing data in the same way. Compare scores, counts between the two analyses. They should be the same.
867. Selecting (only) and sorting table 30.4
henrikalb April 10th, 2008, 3:41am:
Dear Mike,
Is it possible to have only table 30.4 put out in a file and sorted in descending order by column 2 (”SUMMARY DIF”)?
I specified TFILE=*30.4*, but I still get all the 30.x tables.
Furher, why is it, when I specify ”DIF = MA10”, I do not get D.F.=9 for every item in column 3 (”D.F.”) of table 30.4?.
Yours sincerely,
Henrik
MikeLinacre:
Henrik, apologies that sub-table selection has been only partially implemented in Winsteps.
Suggest you copy-and-paste Table 30.4 into Excel. You can then put each table column into a separate Excel column by using "Data", "Text to columns". Then sort the Excel Table how you wish.
”DIF = MA10” stratifies the ability range of the sample into 10 ability level "classes" of the same logit range. For each item, classes that aren't observed or that have extreme scores ("<", ">") are dropped from the chi-square computation. With example0.txt, item 23 has 10 classes, but item 24 has only 4.
MA10 is shown with 10 d.f., instead of 9, because the computation for each class is almost independent. The exact number of d.f. is somewhere between 9 and 10. The larger the sample, the closer to 10.
868. Postulating presence of a hierarchical construct
limks888 April 8th, 2008, 9:07am:
Hi Mike, can you help me on this?
I have broken down my construct of physics competence into different knowledge sub-sonstructs. Tests to measure these sub-constructs are designed based on their operational definitions and given to students. I wish to do a Rasch scaling to place these sub-constructs onto a hierarchical scale based on their responses.
What's the best way I can do this? Hope my question is clear.
Thanks
MikeLinacre:
Thank you for your question, links888.
The equivalent problem faced Richard Woodcock with the different sections of arithmetic tests (addition, subtraction, etc.). At Ben Wright's first AERA workshop in 1969. Richard's solution was to analyze all his items together and then to present them as parallel strands, one per section.
869. Winsteps 3.65 vs. 3.64
ning April 6th, 2008, 3:27am:
Dear Mike,
I have already previously performed RSM analysis using the version 3.64 and listed the Tables to report. I download the 3.65 this morning, performed the same analysis on the same data, the PCA residual output gives totally different results, could you please tell me why? For instance, previously, the raw variance explained by the measure was 82% but now, with the 3.65 version, it's only 52%.
Thanks,
Gunny
MikeLinacre:
Certainly, Gunny. My apologies for these changes and any problems they cause you.
The PCA variance computation has been revised in the light of hard-earned experience. It was discovered that the previous computation was over-stating the variance explained by the Rasch measures. The revised computation more accurately portrays the variance decomposition.
ning:
Thanks, Mike. I'm glad for the software improvement.
gunny
870. Type I error adjustment
ning April 4th, 2008, 11:48pm:
Dear Mike,
Is there a way I can adjust the type I error such as Bonferroni adjustment in Winsteps? If not, the output from the Table 30's are not adjusted results. Where or which tables and how do I export Rasch measures to SAS for such adjustment?
Thanks,
gunny
MikeLinacre:
Correct, Gunny. Table 30 reports individual t-tests. "Is this item biased when considered alone?"
If you want to report Bonferroni adjusted values for multiple t-tests, "Is this item biased when considered as part of a set of items?", multiply the p-value for each item's t-test by the number of items tested or divide .05 (or .01) by the number of items tested.
The choice of unadjusted or adjusted depends largely on whether you think of each item as uniquely special (a content-oriented perspective), or you think of each item as being a random item from a set of items (a G-Theory perspective).
871. Rusch Model in Sosial Science
hash April 3rd, 2008, 11:10pm:
I would like to study the best practises in measure the quality of financial disclosure.
My questions is :
Whether the Rasch Model can be use to measure the quality of Financial Disclosure ?
Need Advise from the members in this forum
Regards
Hash ::)
MikeLinacre:
Thank you for your question, Hash.
The Rasch Model has been applied to many problems in economics and finance.
Pedro Alvarez at the University of Extremadura, Dept. of Applied Economics, has published in this area.
hash:
Thanks Mike
I already find some articles written by
Pedro Alvarez at the University of Extremadura, Dept. of Applied Economics.
872. Constructs and sub-constructs of knowledge
limks888 April 2nd, 2008, 8:50am:
Hi Mike,
I have completed the online course on IRT a few years back facilitated by Andrich and group.
Pls help me on this.
Can we treat, say, 'knowledge types' as sub-constructs of the main psychological construct of "knowledge", or are they merely categories of knowledge.
Lim
MikeLinacre:
Thank you for your question, Lim.
We can treat "arithmetic types" (such as addition, subtraction, multiplication, division) as sub-constructs of "arithmetic", so probably it is the same with "knowledge".
Please try it and see what happens ...
limks888:
Thanks Mike,
I plan to do an IRT scaling to estimate competence of students based on their performance on the different knowledge type tasks.
Lim
873. Error in Winsteps
kuang February 25th, 2008, 11:09pm:
We have a dataset with over 500 items and 2500 people but a lot of missing data. The original data is in SPSS format. I created the control file with the SPSS scroll-down menu. The items are scored as right or wrong, so the items are binary now. I created a smaller dataset just for testing purpose. Only 3 items ion 2778 cases are included in the dataset and I ran the control file I created for this data file. The Winsteps showed that No non-extreme Persons, see RFILE=
Oops! Use "Edit" menu to make corrections, then restart.
However, I don't know what corrections I should make in order to make it run. I need your help. I guess that the missing data is causing this problem, but I am not positive about this. Thanks!
MikeLinacre:
Your diagnosis sounds correct, kuang. With only 3 items and a lot of missing data, it seems there were no response strings like "101". Your RFILE= should currently show strings like "1.." or "0.0". You could add two dummy persons: "101" and "010". These would force Winsteps to run to completion.
ruthmagnolia:
Hi,
I had the same problem that Kuang (only 4 items and many missing values). It seems I resolved it when I removed the IWEIGHT=*
1-4 0
*
command.
Does it make sense? How can it concern my regression analysis?
I tryed with another IWEIGHT values (different from 0) and I got results. Can I trust in them?
Than you very much!
MikeLinacre:
Thank you for your question, Ruthmagnolia.
IWEIGHT=*
1-4 0
*
This instructs Winsteps to ignore items 1,2,3,4 for the purposes of person measurement. Person measures are estimated based on all the other items. Zero-weighted items are reported with difficulty estimates and fit statistics. Zero-weighting can be useful when pilot or exploratory items are included in a test or instrument.
Is this what you want to do?
ruthmagnolia:
Hi,
What I'm trying to do is a regression, following the Wright's instructions. When I did it with a sample of 75 people, I did not have any problem with the command IWEIGHT. But, when I used my complete sample (739 people) Winsteps showed that "No non-extreme Persons, see RFILE=
Oops! Use "Edit" menu to make corrections, then restart."
When I saw the Kuang solution, I did a trial without missing values, but I got the same Winsteps answer.
Thank you very much!
MikeLinacre:
Ruthmagnolia, my apologies. Please email me your Winsteps control and data file, so that I can diagnose the problem.
874. Reliability Index
Inga March 24th, 2008, 7:28pm:
Hi,
We ran a computerized adaptive test (CAT) dataset using the Winsteps program. The person reliability index (Table 3.1) was low (as expected). However, we would like to have reliability index estimated. One way we can think about is to utilize the standard error information from Table 20. Is there any formula that can generalize reliability coefficient (=Cronbach's Alpha) from standard error information from Table 20? Or, this is a wrong direction?
Thanks
Inga
MikeLinacre:
Conventional reliability indices, such as Cronbach's Alpha, are sample-distribution dependent, Inga.
Ben Wright suggests an alternative computation for a reliability index which would apply to a sample with a range equivalent to the operational range of the test. This is at www.rasch.org/rmt/rmt144k.htm
875. Rescaling with multiple pass-fail points
Stampy March 21st, 2008, 1:46am:
Hi Mike,
In the Winsteps documentation, there is an example of user-friendly rescaling in which a pass/fail score is set to a specific desired value on a rescaled metric (Example 7). Is there any way to do something similar with multiple cut points (e.g., on a 1--10 scale, 3 = Basic Proficiency cut point, 5 = Intermediate Proficiency cut point, 7 = Advanced Proficiency cut point, etc.)?
I'm assuming that it is impossible if the distance in logits between the cut points on the original scale are not equal interval (e.g., Basic = -1.0, Intermediate = 0.0, Advanced = 2.5, or some such), but perhaps I'm overlooking something.
Just curious...
MikeLinacre:
You could set two cut-points to friendly values, Stampy, (using UIMEAN= and USCALE=), but the other cut-points would be linearly rescaled. You could probably choose the two cut-points to be the ones which made the values the friendliest overall. OK?
Stampy:
That makes sense. Thanks for the reply.
876. Rasch and continuous data
Belinda March 2nd, 2008, 6:04am:
I am really really new to the concept of Rasch model scaling, as I am sure my query will indicate - is it possible to use Rasch with continuous data, or does it have to be dichotomous?
Any help would be much appreciated.
MikeLinacre:
Thank you for your question, Belinda.
There are Rasch models for continuous data, but they are not convenient to use and rarely productive.
The reason is that empirical data tend not to be continuous, but "chunked", and the ordinal relationship between the "chunks" is not smooth.
Consequently it is usually more productive to statify the continuous data into 9 or less levels, and then ordinally number the levels: 1,2,3,4,5,6,7,8,9. It is the level numbers that become the raw data for Rasch analysis.
There are more comments about this half-way down https://www.winsteps.com/winman/decimal.htm
877. Processing agreement by levels using FACETS
SusanCheuvront February 28th, 2008, 9:04pm:
I have a constructed-response test here that consists of 5 levels--the first level containing the easiest items, the fifth level containing the most difficult items. Examinees have to get a certain number of items correct at each level to obtain a given score. Each examinee's test is scored by two independent raters. I'm trying to look at rater agreement by level, to see if more disagreements arise in any given level. I'm not sure how to input the data into FACETS. There are 12 items at each level. Can I set it up like this:
1, 1, 8, 10, 7, 5, 6 : Rater 1 rates examinee 1 8 at level 1, 10 at level 2, 7 at level 3 5 at level 4 and 6 at level 5.
Would each level be a facet, then?
MikeLinacre:
Thank you for this conundrum, Susan.
The Facets are:
1= Rater
2= Examinee
3= Level (5 elements)
It seems that at each level, the examinee is given a score out of 12 by the rater. So this is equivalent to a rating on a (0-12) = 13-category rating scale.
Then your example data would look like:
1, 1, 1-5, 8, 10, 7, 5, 6 : Rater 1 examinee 1 levels 1-5, ratings: 8, 10, 7, 5, 6
The Facets specifications would be:
Facets=3
Models = ?,?,#,R12 ; assuming a different 0-12 structure at each level
Inter-rater = 3 ; for summary inter-rater agreement statistics by level.
878. How to handle missing when no right/wrong ans.
ning February 25th, 2008, 11:06pm:
Dear Mike,
What's the best way to handle missing data when the ratings do not involve right or wrong answers? For example, ability scales. Do we treat missing as missing, or should we impute the missing value to ensure consistent residuals?
Thanks,
MikeLinacre:
If the "missing data" does not indicate more-or-less of the intended latent variable, Gunny, then code it "not-administered", i.e., give it a non-numeric value, such as "." or "*"
ning:
Thanks, Mike,
What if the missing data does represent more or less of the latent variable? is "not-administrated" the same as "treat it as missing?" Will MLE statistically account for missing data problem? Will a paired comparison always necessary in this situation?
Thanks, Gunny
MikeLinacre:
Gunny, if a missing-data-code indicates "less of the variable" (as it does conventionally on MCQ tests), then code it "wrong" as opposed to "right". If a missing-data-code indicates "more of the variable" (as it does on some attitude surveys and personaility tests), then code it "yes" as opposed to "no".
In general, there is always data "missing" because we can always imagine more relevant questions, that we didn't ask, or other relevant persons, whom we didn't include in our sample. The usual idea of "complete" data is of a rectangular dataset that is completely filled, but this is only a constraint of some raw-score analyses. It is not a constraint of Rasch analysis, and is irrelevant to MLE. Effective MLE methods maximize the likelihood of the observed data and ignore data coded not-administered.
879. Batch processing to output table 1.2 only
cmeador February 23rd, 2008, 10:10pm:
I have many control files for which I would like to output Table 1.2 (but nothing else). I have made some good progress with the help files on batch processing and command line options, and so far the closest I have come to what I want is the following:
for %f in (*.txt) do START /WAIT ..\Winsteps.exe BATCH=YES %f %f.out TFILE=* 1.2,-,-,- *
This command iterates through all of the control files stored in a subdirectory of my Winsteps folder and outputs Table 1.2 for each control file to a new file called controlfilename.out. Then I can concatenate all of the .out files into a single text file with all of the tables.
The problem I am having is that this command will output Table 1.2, but then it will also output Table 1.10, Table 1.12, Table 0.1, Table 0.3. How can I suppress this extraneous output so that I am left with only Table 1.2?
Thanks in advance!
PS, I am running Winsteps 3.64.1 on Windows XP Pro.
MikeLinacre:
It looks like you are already doing the best that can be done, cmeador. If Table 1.2 is output first than you may be able to organize your concatenation procedure to drop subsequent Tables. You could indicate when they begin by choosing a suitable character for FORMFEED=. This character would be output in the heading line of all tables after the first.
cmeador:
Thanks for the quick reply! The formfeed characters should make processing the output files pretty easy to script, I just thought there was something about TFILE that I was misunderstanding. Thanks again!
880. mforms troubles
harmony February 21st, 2008, 10:54pm:
Hi all:
I attempted to combine two tests linked by common items into one form using the mforms command. I followed the examples given in Winsteps help. I encountered confusion on the following points, however. How much of an original control file is changed when mforms is added, or should it be a separate file on its own? If the commands are referring Winsteps to the data of the two files for the test, why is it necessary to add additional Item labels?
I tried to use mforms in numerous experimental ways building off of example files in the help menu, but the closest I got resulted in text and command lines being included in the analyzed data when viewed in data setup. Why would this be so.
Determined to see what the tests would look like together, I ended up manually altering the control file for one test, the data files for both tests, and then pasting all of the data into one file without mforms. It was successful, but highly labor intensive as the linked items were not in a sequence, but were scattered throughout the two tests and this resulted in a great deal of moving data around, and spacing data out.
Any insights pointers, or further information on how to use mforms without so much effort would be greatly appreciated. I'm sure that if I used the command correctly, I would have been able to combine my tests with much less effort.
MikeLinacre:
Yes, MFORMS= is complex, harmony.
It attempts to do what you did manually in your paragraph "Determined ....".
In your situation you need the following:
1. Original Test 1: Data file only = datafile1.txt. But analyze this first with a control file including DATA=datafile1.txt
2. Original Test 2: Data file only = datafile2.txt. But analyze this first with a control file including DATA=datafile2.txt
3. Combined Test: Control file (including MFORMS=) with no data, but with MFORMS= referencing datafile1.txt and datafile2.txt. See MFORMS= Example 3 in Winsteps Help.
For the Combined Test, you decide on the ordering of the items, so copy-and-paste the item labels from the control files for Original Test 1 and Original Test 2 to match your combined ordering. Yes, it would be better if this was automated, but I discovered there were too many different possibilities ... I should go back and look at this again.
881. Items Characteristic Curves and group-markers...
Andreich February 18th, 2008, 5:41am:
Hello! I have a question about Items Characteristic Curves (ICC)... When we use test with 2 category (0 - 1), the Y-position of the group-marker defined as part of persons who give right answer on this item. But how we define Y-position if test contain more then 2 category (for example . 0 - 1 - 2)?
MikeLinacre:
Andreich, ICCs for polytomous items (0-1-2-..) have the rating scale on the y-axis. So the y-position for a group is the average score of the group on the item, e.g., 1.32. OK?
Andreich:
If I correctly understand, than...
P001_answer = 2
P002_answer = 1
P003_answer = 3
P004_answer = 3
----------------------------
Total = 9
Y-pos = 2,25
Am I right?
MikeLinacre:
Yes, you are right, Andreich. P001, P002, P003, P004 all need to be in the same interval on the latent variable (X-pos) for the Y-pos to make sense as part of an empirical ICC.
Andreich:
Now, all is clear for me. Thank you for help, Mike!
882. Beta verion of html vertical rulers from Nov Facet
ImogeneR February 13th, 2008, 2:24am:
Hi Again,
In the november FACETS course last year Mike you had us beta test a great new way of getting the vertical rulers to display in a publication friendly html type format. I can see form the previous 'coming in winsteps' post that there should be a way to se ascii=yes etc either through initial settings or modify output but the ascii options aren't appearing on my screens..do I have the wrong version? It's 3.62.0 June 2007.
Cheers
Imogene
MikeLinacre:
Imogene, the HTML feature is in the current version of Facets 3.63.0 Jan. 2008. I've emailed you download instructions.
883. judging plan
seol February 3rd, 2008, 4:14am:
Dear Dr. Linacre :)
Hello? This is Seol. I have a question about judging plan.
In a writing assessment, each students performance would be evaluated as to each of the four-trait within the item, based on the judgement of two or three raters.
That is, each student paper will be rated two or three times for each trait. In this case, the problem is that the number of students are very large(apprx 3000 students). so the completely crossed design is not suitable for my study. so modified nested or mixed design, I think, should be cosidered. In this case, when cosidering time and costs, Could you tell me the appropriate design to run facet-model in this case?
Thanks in advance
Best Regards
Seol
MikeLinacre:
Thank you for asking, Seol.
Best would be a linked network of raters. Organize the raters so that the ratings given by any rater can be compared, directly or indirectly, with those of any other rater. See www.rasch.org/rn3.htm has examples.
ImogeneR:
Hi Seol and Mike,
I am still struggling with the concpet of judging plans too and have read a couple of studies using Facets that argue that two raters must judge a single candidate performance on an item for any judge severity-leniency comparisons can be made.
In the reference quoted above though the rating constraints were 1) each essay be rated only once, each judge rate an examinee only once and 3) each judge avoid rating any one type of essay too frequently.
We have a situation where candidates are rated by only one judge on each question and there are different subsets of questions used in the examination (so not all candidates do all questions and not 2 judges compare the same candidate on the same question). Facets subset connection is OK. Does this mean we can say that our analysis is able to measure judge severity/leninency even though other authors have said you must have 2 raters view a single candidate on a single question?
Many thanks,
Imogene
MikeLinacre:
You are correct, Imogene.
This statement is incorrect: "two raters must judge a single candidate performance on an item".
The Facets "minimum effort judging plan" requires candidates to be rated on more than one item. But each item for each candidate is rated once by a different rater. The raters are crossed so that every rater can be compared with every other rater indirectly.
ImogeneR:
Excellent, thanks.
884. RUMM2020 'Subscript out of range' error
rummE February 4th, 2008, 4:31pm:
I'm using the RUMM2020 software and trying to find an ICC for one item. The data set also contains ID, gender and disease group variables. There are no missing values in the data. Can someone tell me what the 'Subscript out of range' error means? How could I fix it?
MikeLinacre:
Please contact: rummlab -at- arach.net.au
which is the RUMM2020 support email addresss
rummE:
I've tried to e-mail rummlab twice, once about a month ago, and once last week. I have had no reply. Thank you for the suggestion though.
When I try to reopen the project, RUMM gives me another error. It says "The total number of items for the Project cannot be obtained from the dataBase. This should have been saved when the Project was created. The Data Base Project file will need to be checked for this error or the Project re-created again."
I also rechecked my data to make sure that it is not the problem.
Any ideas are helpful and appreciated.
MikeLinacre:
There is a RUMM-specific Listserv called "The Matilda Bay Club". https://lists.wu-wien.ac.at/mailman/listinfo/rasch - please join it and post these questions there.
It does seem that the bug which caused the "Subscript out of range" problem has also corrupted the RUMM database. Starting again from the beginning, setting up a new datafile and analysis, may be the only solution.
885. I need help about ability estimation
ayadsat February 1st, 2008, 2:50pm:
Dear friends
I have problems in the ability estimation for example:
I have 4 items each item contains 3 Questionnaires and each Questionnaire contains 3 categories as shown below:
Item No.1:
Questionnaire 1: Low moderate High
Questionnaire 2: Short Medium Long
Questionnaire 3: Bad average Good
My question is How to compute the user ability when user gives three responses at each item ? which mathmatical equation that will be used?
note: Every questionnaire is correlated with item difficulty.
User pattern is (Low Long Average)-->(High Medium Good)-->(High Short Good)-->(High Short Good)
I appreciate your Help.
MikeLinacre:
Ayadsat, thank you for your question.
Simplest would be to number your 4 items x 3 Questionnaires as 12 item-responses.
So your Rasch dataset would have 12 "item" columns per person.
Alternatively, use software which allows more than one response per item, but this is likely to be confusing to explain to others.
ayadsat:
Thank you very much Prof. MikeLinacre for your reply
In fact I want to program this problem by myself by using php and I want to compute user ability at each item, I have problem in the difficulty parameter in the rasch model, can i use the same difficulty parameter in the in the rasch model for each response or I use Partial Credit Model if i will use this model how to compute the difficulty of completing certain step of item i (bij)?
for example : P(X=High)=Exp(ai-bij)/1+Exp(ai-bij).
Best Regard
MikeLinacre:
Ayadsat, this may help: www.rasch.org/rmt/rmt122q.htm "Estimating Measures with Known Polytomous (or Rating Scale) Item Difficulties"
886. Item anchoring across years in FACETS analysis
ImogeneR January 29th, 2008, 10:48pm:
Hi
As threatened here is my second (no doubt long winded!) query post re FACETS.
In this one I'm trying to work out why my attempts to anchor common stations used over two years of administrations doesn't seem to be working..
As mentioned this is the shape of our data:
The data we are looking at involves raters, applicants and items (or stations). It works a bit like an OSCE assessment in that applicants rotate through 8 stations (get a mark out of 20 for each). At each station they are assessed by one rater. raters see numerous applicants at the same stationn and raters may also rate at more than one station. So applicants have 8 ratings from 8 different raters. No rater sees the same candidate twice and there are no common raters for a single person on the same question.
What I am trying to do is anchor the items that were used in 2006 and then again in 2007 with their 2006 measures in a FACETS run of the 2007 data. I want to do this because I see that the measures for stations jump around from year to year (I know this is expected a bit) but I want to see if it can help with establishing any measure of consistency with judge severity/leniency too (we have common judges across the years too).
I used the anchor output file for 2006 FACETS run for items and put the 'A' after the item facet heading in the 2007 control file and then put the 2006 measure next to the item element label as it appears in the output file and as directed in the FACETS course manual section on element anchoring.
The problem is, in the new analysis for 2007 all it appears to do is read this item measure from 2006 as another item label...doesn't seem to impact on the analysis at all...can you see any obvious errors I am making?
Any help much appreciated.
Many thanks
Imogene
MikeLinacre:
Imogene, not sure what your Facets specification file looks like, but would expect this:
Labels=
....
*
3, items, A
1, item 1, 3.7236
.....
*
ImogeneR:
Thanks for getting back to me so quickly.
Yes, that is what the specifications look like, but it doesn't seem to have any impact on the analysis (I was looking for a difference in measeures, or fit or anything compared to running the analysis without anchors) but all that occurred was that I got a different label for the item in the measures output tables ( labelled as the anchor measure).
Cheers
Imogene
MikeLinacre:
Imogene, I'll be happy to investigate. Please email me your Facets specification and data file: mike --/at/-- winsteps.com
887. judging plans and bias in Facets
ImogeneR January 29th, 2008, 10:33pm:
Hi,
Mike I did your Factes course in November which was fantastic but I guess it's afterwards when working wiht the data and the more you know the more you realise you don't know... ;)
Anyway I have a couple of questions about ancoring items across years and bias interactions that I will put in different posts in case anyone else has similar issues.
The first one is about looking at bias and judging plans. The data we are looking at involves raters, applicants and items (or stations). It works a bit like an OSCE assessment in that applicants rotate through 8 stations (get a mark out of 20 for each). At each station they are assessed by one rater. raters see numerous applicants at the same stationn and raters may also rate at more than one station. So applicants have 8 ratings from 8 different raters. No rater sees the same candidate twice and there are no common raters for a single person on the same question. I think this last bit is important - does this mean we cannot use the bias interaction tables because there are no direct comparisons of raters to the same applicant and the same station available? My reading of Bond & Fox MFRM chapter suggests that we have actually got enough linkage to look at bias etc , and facets says subset connection is OK..is this enough to make inferences about a rater being "more severe with applicant x than the rater was overall for this question" from table 13? Because we have so many raters and applicants FACETS gives hug output for these tables and I'm not sure how to make the best of this output. Would it be better to just look at the bias tables of rater to station?
I apologise if this is many questions in one post!
Thanks
Imogene
MikeLinacre:
Imogene, thank you for your questions.
Yes, you can do a rater bias analysis.
How about doing this from the "Output Tables" pull-down menu: Tables 12-13-14
Then you can select the facets "rater" and whatever.
You can also limit the amount of output by choosing high values for the "bias reporatable size" and "significance". Start with 1 and 3, and then adjust the values smaller or larger.
888. Collapsing and Newscore
Raschmad January 26th, 2008, 7:53pm:
Hi Mike,
Id be thankful for your reaction to this.
I want to rescore some of the items because the wording of some items require reversed coding from 5 to 1. The challenge is that because of disordered structure calibration I need to collapse categories too. How should I do both simultaneously? For both I need newscore command. But I need to tell Winsteps to apply the new score -reversing of codes- only to some of the items but collapsing to all the items. I have used these commands
CODES =12345
NEWSCORE=54331; collapsing and reversing of values is executed
RESCORE=0010111110110110110110110010000001010101
Newscore command gives a value of 5 to previous values of 1, values of 4 to 2 and so on.
Rescore applies newscore to certain items which are specified by 1. This means that collapsing is not done for those specified by 0 in Rescore. How should I apply rescoring to certain items but collapsing to all?
Thanks
MikeLinacre:
Fine, Raschmad.
IREFER=0010111110110110110110110010000001010101
CODES =12345
IVALUE0=13345
IVALUE1=54331
and you also need to choose between
STKEEP=YES ; keep the unobserved 2 level
and
STKEEP=NO ; recount levels to remove 2
You may also want to
ISGROUPS = 2212111112112112112112112212222221212121
so that all the forward and all the reversed items belong to one rating scale structure each.
890. Disordered Structure Calibration s
Raschmad January 19th, 2008, 4:32pm:
Hi everyone,
I analysed a rating scale with 5 categories using Winsteps. I was under the impression that the whole test has one category structure report (does it?). But apparently, every single item has one category structure (table 3.2).
For many of my items the structure calibration is disordered between categories 2 and 3. Category measures are fine. And some of the structure calibrations which are not disordered are very close to each other, they increase by 0.10 logits.
Variance explained by measures is 42% and unexplained varance in1st contrast is 4.9%.
Does this mean that persons can’t make a distinction between categories 2 and 3?
There’s an item whose structure calibration for categories 2 and 3 are the same!
There are few undefitting items, few overfitting ones and many underfitting persons.
I collapsed categories 2 and 3 using newscore=13345.
The problem of structure calibration disorder was solved. (Althogh I got rid of category 2, I still get category measure for it!). However, the variance explained by measures reduced to 37.9% and unexplained variance in1st contrast raised to 5.1%.
What Can I conclude about the instrument? :(
Thanks
MikeLinacre:
Raschmad, thank you for your questions. You need to think about the substantive meaning of your rating scale categories.
1. "every single item has one category structure (table 3.2)."
If you omitted "GROUPS=", then all items share the same rating scale structure. If you specified "GROUPS=0", then each item has its own rating scale structure. Which would make the most sense for your audience?
2. "many of my items the structure calibration is disordered between categories 2 and 3."
If the Rasch-Andrich thresholds are disordered, then the observed frequency of a category is relatively low. Why is this? Look at the category definitions: is one category worded to be narrower than the others? Are respondents being asked to make too fine a distinction in qualitative levels? Or are the rating scale category definitions well-ordered, but the sample behavior idiosyncratic or the sample size small?
A general rule is that there must be 10 observations per category before stable rating-scale structures can be expected.
3. Disordered categories (e.g., categories numbered out of qualitative sequence) usually cause noticeable "noisy" misfit. Disordered Rasch-Andrich thresholds (i.e., relatively low frequency categories) usually have no impact on fit.
4. Collapsing categories: "variance explained by measures reduced to 37.9%"
so, in collapsing categories, you have lost more useful measurement information than you have gained(?) in simplifying the rating scale. A further reason to think carefully about the meaning of your rating scale.
General rule: "meaning is more important than numerical tweaks", or, as Albert Einstein wrote: "It is really strange that human beings are normally deaf to the strongest arguments while they are always inclined to overestimate measuring accuracies."
891. Help! FACETS is giving me an error message
SusanCheuvront January 15th, 2008, 10:39pm:
Lately when I've been running FACETS, I've been getting an error message and I can't figure out why. There doesn't seem to be anything wrong with the input file. The error is F1 in line 1 and says that specification isn't found. It's expecting "specification = value," when my first line is Facets = 2. It looks like FACETS is reading an extra character when there's no extra character. Can anybody advise?
thanks
Susan
MikeLinacre:
Sorry to read of these difficulties, Susan.
First, check that your Facets specification is a standard text file (not a Word file, etc.)
Open the file with NotePad.
Look at it. Does all look OK?
Save it as "Encoding: ANSI" - even though nothing seems to have changed.
Then, Facets usually reports the line details along with the error message. What does that say? If you are not sure, please copy your screen (PrintScreen key then paste into a Word document) and email it to me.
892. Quick Winsteps set up Query
ImogeneR January 15th, 2008, 1:44am:
Hi,
Is there anyway of creating more than one label for an item in the Winsteps control file?
Thanks
Imogene
MikeLinacre:
Imogene, thank you for your question.
How about this?
One set of item labels in your Winsteps control file.
Then, when you need a different set of labels, use the
"Specification" pull-down menu
ILFILE=pathname.txt
where pathname.txt is a text file with a different set of item labels.
893. time points for rack and stack
ning January 9th, 2008, 5:14pm:
Dear Mike, happy new year!
Can more than two time points be used in racking and stacking?
Do you have a good reference on its application that you can recommend?
Thanks,
MikeLinacre:
Gunny, with improvement in Winsteps, there is no need to "rack". You can certainly "stack" as many time-points as you like. Include an indicator variable in the person label to indicate time-point.
For three time-points, google "rasch admit discharge follow-up"
ning:
Thanks, Mike.
In this case, changes for multiple time points in Winsteps can be assessed as one of the person indicator and look at the DIF between different time points. Conceptually.....if I want to look at the main effect of time using Facets, are these approaches still the same? Thanks,
MikeLinacre:
In this situation, the difference between "stacking" the data in Winsteps and parameterizing the time-point in Facets would be:
"stacked" Winsteps would report the time-point effect but allow each person to have their own measure at each time-point. Each person receives one person measure per time point.
"parameterized' Facets would force the time-point effect to be the same across persons and adjust the individual person measures accordingly. Each person receives one person measure.
894. LLTM Design Matrix
Dirk January 4th, 2008, 10:21am:
Dear Mike,
I have some doubts about my design for a study on program source code. The problem is that I have on the one hand the true items (I, the questions) and on the other hand different source codes (C), so my lltm design matrix looks roughly like this:
I1 I2 I3 I4 C1 C2 C3
1 0 0 0 1 0 0
0 1 0 0 1 0 0
0 0 1 0 1 0 0
0 0 0 1 1 0 0
1 0 0 0 0 1 0
0 1 0 0 0 1 0
0 0 1 0 0 1 0
0 0 0 1 0 1 0
1 0 0 0 0 0 1
0 1 0 0 0 0 1
0 0 1 0 0 0 1
0 0 0 1 0 0 1
Item easiness thus consists of two eta parameters - one for the item and one for the source code. I am not sure that this is allowed as I only found example matrices using additional eta parameters for indicating a change over time.
In addition - is it allowed to interpret eta parameters? I found a warning to do this, but I really would like to interpret them.
Best regards,
-Dirk
MikeLinacre:
Dirk, thank you for asking about LLTM matrices. It is a long time since I heard Gerhard Fischer explaining these, but I think you need to do the following to remove the ambiguity in your matrix:
Organize your LLTM matrix so that one item has an I-parameter, but no C-parameter.
"allowed to interpret eta parameters?" - don't see why not.
Dirk:
Thanks for the answer Mike - I just thought I could integrate the treatment as a parameter in the q-matrix. But I am greedy sometimes ;)
-Dirk
MikeLinacre:
Dirk, how about contacting Patrick Mair or Reinhold Hatzinger, they appear to be experts: patrick.mair /at/ wu-wien.ac.at reinhold.hatzinger /at/ wu-wien.ac.at
Dirk:
Hi Mike,
Yes, I will do that - although it was the documentation of their eRm package that included the warning about eta parameters ;)
-Dirk
895. Winsteps vs. Facets
ning January 9th, 2008, 5:35pm:
Dear Mike,
How's the results differ for the time 1&2 (or more) analysis using Winsteps compared to Facets? Thanks,
MikeLinacre:
Gunny, if the analyses are set up the same way, then Winsteps and Facets will report the same numbers.
Usually I would recommend Winsteps for this. Include "time point" as an indicator column in the person label. You can then do Time 1 vs. Time 2 DIF studies on the items, and also Time 1, Time 2 subtotals,
896. local measure vs. relative measure
ning January 9th, 2008, 11:07pm:
Dear Mike,
Another question on rack and stack please.....what's the best way to assess the change from time 1 to time 2? If the DIF plot is used, the local measure and relative measure look drastically different, how to interpret the two plots and which one should be used?
Thanks, Mike.
MikeLinacre:
Gunny, the relationship is:
local measure = overall measure + relative measure
So, if an item has overall difficulty estimate of 2.0 logits, and for Alaskans it is 1.0 logits more difficult than overall, then the relative measue is 1.0 logits and the local measures is 2.0+1.0 = 3.0 logits.
So, whether we use local measure or relative measure depends on what question we want to answer.
1. Is item 4 easier for Alaskans or Hawaians? - answer "relative measure" (if we want to exclude the overall difficulty of item 4) or "local measure" (if we want to include the overall difficulty of item 4).
2. Is item 4 easier for Alaskans than item 5 is for Hawaians? - answer "local measure".
898. output reading
happiereveryday January 2nd, 2008, 7:51am:
Dear Mike,
Sorry for another two basic questions but I can't solve them by reading the manual.
1. In examinee measurement report, rater measurement report and item measurement report, there are infit MnSq and out fit MnSq. I know values larger than 2 or smaller than 0.5 are not acceptable, but how to interprete them in different measurement reports?
2. What are Infit ZStd and Outfit ZStd? They co-occur with Infit MnSq and Oufit MnSq, what are their relationships? Are they some kind of Z score?
3. chi-square also occur in examinee measurement report, rater measurement report and item measurement report. Are they check the hypotheses "do the examinees have the same ability?", "do the raters have the same severity?" and "do the items have the same difficulty?" respectively? My data is not categorial, but scores (prefect score is 100), how can they fit chi-square tests?
Sorry for these basic questions. Looking forward to your reply,
MikeLinacre:
Thank you for these questions, Happiereveryday.
My answers would be rather long, so for 1. and 2. please look at
www.winsteps.com/facetman/index.html?diagnosingmisfit.htm
For 3. please see https://www.winsteps.com/facetman/index.html?table7summarystatistics.htm
These are also in Facets Help
899. quesions on reading the output
happiereveryday January 2nd, 2008, 1:24am:
Dear Michael,
Thank you for your reply. I've reinstalled Facets and it works now. I have two more questions.
1. In my data there are 4 facets, examinee, gender, rater and item. I set Positive = 1; for examinees, higher score=higher measure. In output Table 6 (All facet vertical rulers), does higher measure mean higher examinee ability, more lenient rater, easier item?
2. My Models=?,?,?,?,R100; the rating of items are from 0-100(perfect score is 100, though actually the highest score is 96). In category probability curves, are there 96 categories (96 curves)?
MikeLinacre:
Thank you, happiereveryday.
1. In Table 6, look at the top of each column. "+" means "higher score and higher measure", so you should see "+examinee". "-" means "higher score and lower measures". So you should see "-gender", "-rater", "-item".
2. Models=?,?,?,?,R100 - this produces as many curves as there are different categories observed between 0 and 100, but it compresses out unobserved intermediate categories.
Models=?,?,?,?,R100K - this produces as many curves as there are different categories observed between 0 and 100, but it keeps intermediate unobserved categories.
Models=?,?,?,?,B100 - this models percents as 100 binomial trials and produces 101 category curves. You could try this to see if it matches your data.
900. running error
happiereveryday January 1st, 2008, 8:06am:
Dear Michael,
My Facets can not run now. When i try to open a file, a dialogue box says,"Run-time error '429', ActiveX component can't create object." What's wrong with it?
Thank you for your reply!
MikeLinacre:
Happiereveryday, sorry to hear this. 429 is an error that can have many causes.
1. Reboot your computer - try again.
2. Uninstall the software (Winsteps or Facets), then reinstall it. - try again
3. If the software still fails, then more complicated diagnosis is required.
| Rasch-Related Resources: Rasch Measurement YouTube Channel |
|---|
Rasch Measurement Transactions &
Rasch Measurement research papers - free |
An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse |
Rasch Measurement Theory Analysis in R, Wind, Hua |
Applying the Rasch Model in Social Sciences Using R, Lamprianou |
El modelo métrico de Rasch:
Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition),
Manuel González-Montesinos M. |
| Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar |
Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
Rasch Models for Measurement, David Andrich |
Constructing Measures, Mark Wilson |
Best Test Design - free, Wright & Stone
Rating Scale Analysis - free, Wright & Masters |
| Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias |
Diseño de Mejores Pruebas - free, Spanish Best Test Design |
A Course in Rasch Measurement Theory, Andrich, Marais |
Rasch Models in Health, Christensen, Kreiner, Mesba |
Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen |
| Rasch Books and Publications: Winsteps and Facets |
|---|
| Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene |
Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver |
Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone |
Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale |
Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland |
| Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes |
Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang |
Statistical Analyses for Language Testers (Facets), Rita Green |
Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind |
Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M |
| Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind |
Rasch Measurement: Applications, Khine |
Winsteps Tutorials - free
Facets Tutorials - free |
Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre |
Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan |
| Rasch Meta-Metres of Growth for Some Intelligence and Attainment Tests: A Meta-metre for some Intelligence and Attainment Tests, David Andrich, Ida Marais, Sonia Sappl |
|
|
|
|
| Coming Rasch-related Events |
|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |

