Old Rasch Forum - Rasch on the Run: 2009
Rasch Forum: 2006
Rasch Forum: 2007
Rasch Forum: 2008
Rasch Forum: 2010
Rasch Forum: 2011
Rasch Forum: 2012
Rasch Forum: 2013 January-June
Rasch Forum: 2013 July-December
Rasch Forum: 2014
Current Rasch Forum
217. Item Calibration by Hand
Sue_Wiggins March 9th, 2009, 1:03pm:
Greetings from a Rasch novice the UK.
Please could somebody help with item calibration by hand? I am simply doing this as an exercise so I understand Rasch. I am using the Prox example given in the book 'Best Test Design'. May I say this is brilliantly written and explains well but my algebra knowledge is not brilliant. To get to the point; on p.35 there is a table and I understand the vast majority of it. However, all I really want to know concerns the last but one row (where all the albegra is). What is 'U' ? Also please could you explain how ...
10
∑ f i x 2 = 0.51
i
In other words where does the .51 come from. As I understand the algebra following 'U = ' is the calculation variance but this is not the algebra I understand to be the variance which is simply
∑ d2 / N-1
Any help appreciated
Regards
Sue :-/
Sue_Wiggins:
Hi again
Just to say apologies for the problems with the math symbols - they looked perfect before I sent the message. Obviously there are some software issues.
Sue
MikeLinacre:
Certainly we can help, Sue.
You have U correct, but remember that that is "computation by hand", so we take intermediate steps that we would not do with a computer.
U is intended to be the unbiased variance of p. 35 column-6 (remembering that each entry in column-6 occurs column-3 times).
For the 0.51 value:
sum-column-3 * (sum-column-7 / sum-column-3)**2
Sue_Wiggins:
Hi Mike
Thanks for your reply but not sure what you mean by your last line exactly. Summing column 3 gives you N (14) I know the sum of column 7 divided by sum of column 3 gives you the mean logit (2.64) but not sure what your asterisks mean and what the 2 at the end is for. However, after studying the table in detail again I realise that .51 comes from taking the sum of the deviations squared (that's squaring each of column 9 then summing = 74.30) from the sum of the logits squared. As I understand it's really just the usual variance formula.
Sue
MikeLinacre:
Yes, that is the usual variance formula, Sue, in a form convenient for computation by hand.
**2 means "squared". It is sometimes written ^2
Sue_Wiggins:
Thanks once again Mike. That is really helpful. Thank goodness for your help and this forum. I am sure I will be here again soon.
Best wishes
Sue
Emil_Lundell:
I have negative expansion factors for test width and sample spread, something have gone hideously wrong!
On p. 40 Wright & Stone uses the values 2,89 and 8,35 and on p. 21 they explains that it has to do with logistic and normal ogives. Should these two values always be used? Or do the values vary?
If they vary how do I calculate them?
Mike.Linacre:
Emil, the values 2.89 and 8.35 = 2.89^2 are values for conversion between the cumulative normal ogive and the logistic ogive. They are constants, but my own investigation suggests they are too large: https://www.rasch.org/rmt/rmt112m.htm
Expansion factors can never go negative because they are based on variances, which are always positive.
Emil_Lundell:
[quote=Mike.Linacre]Emil, the values 2.89 and 8.35 = 2.89^2 are values for conversion between the cumulative normal ogive and the logistic ogive. They are constants, but my own investigation suggests they are too large: https://www.rasch.org/rmt/rmt112m.htm
Expansion factors can never go negative because they are based on variances, which are always positive.
Thanks Dr. Lineacre,
Then these values isn't the problem. But I still can't calculate the expansion factors and I can't find where I made the mistake. Can you help me please? I have attached a docx file.
Emil_Lundell:
Something is strange with the wordfile. Here's a PDF with the same information.
I'm aware that it should be "scale factor" and not "expansion factor" before the conversion values, type error.
685. slope of the best fit line
william.hula December 29th, 2009, 3:40pm:
Hello,
In common-person equating, to calculate a scaling constant in casese where the slope of the best fit line is far from 1, the WINSTEPS manual advises using the slope of the best-fit line calculated as (SD of Test B common persons / SD of Test A common persons). The MS Excel SLOPE function, however, gives a slope that is equal to this value multiplited by the correlation of the two variables.
It seems that the WINSTEPS manual recommendation provides a slope estimate under the assumption that the two variables correlate perfectly. Do I understand this correctly, and if so, what is the rationale for doing it this way? Also, what would be consequences of using the slope value provided by the SLOPE function in Excel?
Happy Holidays,
Will
MikeLinacre:
Thank you for your questions, William.
There are numerous computations for "best fit" line, depending on how "best fit" is defined.
An essential check on any best fit line (for equating purposes) is that switching the X and Y axes should produce the same relationship between the two sets of measures.
Winsteps uses a convenient definition which is easy to compute and confirm by hand. It assumes that all the measures are approximately equally precise (same standard errors). Since everything is measured-with-error, any best-fit-line is only provisional.
If different choices of best-fit-line lead to noticeably different findings, then the equating is precarious. A fundamental rule in science is that different reasonable approaches to a problem should result in effectively the same conclusion. When this does not happen, then there is an interaction between the data and the approach, threatening the validity of the findings.
william.hula:
Thank you!
686. unidimensionality
newrasch December 1st, 2009, 5:11pm:
Hello, can someone please help me with the following questions?
(1) What are the possible consequences from conducting a rasch analysis when we violate unidimensionality?
(2) Does dimensionality have anything to do with differential item functioning? why or why not?
Thanks!
MikeLinacre:
Glad you can join us Newrasch!
1. If we intend the data to be unidimensional (so that we can align all the performances along a line), then a violation of unidimensionality contradicts our intention. Unidimensional Rasch analysis always reports measures along a line, but also reports fit statistics and other indications of how much and where the data depart from our intention.
2. Multidimensionality can occur in many ways. If there is a boy-girl dimension on a math test, then that dimension will appear as differential item functioning (DIF). But if there is an addition-subtraction dimension, then that dimension may impact boys and girls the same, and so not appear as DIF.
msamsa:
So, what are the procedures in order to know if the data is unidimensional by Winsteps? As we know in SPSS, there is a clear procedure and calculations to verify the dimensions in the data.
MikeLinacre:
Mamsa, thank you for your questions. Please look at Winsteps Help (on your disk or on the web). Here are some topics that may answer your questions:
https://www.winsteps.com/winman/index.htm?dependency.htm
https://www.winsteps.com/winman/index.htm?dimensionality.htm
https://www.winsteps.com/winman/index.htm?multidimensionality.htm
wlsherica:
I recommend Winsteps manual for learning Rasch model, it's really helpful!
msamsa:
thank you all
687. Category misfit
Raschmad December 26th, 2009, 10:11am:
Dear Mike,
I have analysed a data set with rating scale model. The theresholds, category measures and category averages are orderd. Only the first category misfits. What does this mean?
When I analyse the same data set with partial credit model the raw score for itmes do not accord with their measures. An item with a raw score of 35 has a lower measure than items with raw scores of 250 and an item with a raw score of 313 has a measure higher than items with raw scores of 220-250. However, when RSM is used this problem doesnt crop up. Why does this happen and what does it mean?
Raschmad
MikeLinacre:
Thank you for your questions, Rashmad.
Category misfit: a few very unexpected observations of a category could cause large category misfit, but not enough to give damage the ordering. The observations are probably listed in the 'unexpected responses" output tables.
Andrich RSM vs. Masters PCM: When we use PCM we allow each item to define its own rating scale. A result is that we see output that looks like what you describe. Please look at the observed categories for each item. If the lowest and highest categories differ across items, then the PCM results will differ considerably from the RSM results.
688. Scores change in Rasch
wlsherica December 6th, 2009, 2:02pm:
Hi, Mike,
I'd like to measure change in quality of life (QoL) scores from the baseline data.
Now I had baseline scores(Q0) and the one after 3 years(Q1) and I'd like to get
the score change during 3 years.
Does it work or reasonable that I just analyze these two QoL scores separately in Winsteps, pick both of person measure, say Q0 and Q1, then Q1 minus Q0, the value I got from (Q1-Q0) could be used for further analysis?
Or I need to anchor the baseline data?
BTW, if there were some missing data in Q1, should I delete them both in Q0 file and Q1, just use the complete data?
Now I'm trying to persuade my classmates, all of them are physicians, and show them using Rasch analysis in quality of life is better than classical test theory. I hope I can succeed in it.
Thanks!
MikeLinacre:
Thank you for your questions, Wisherica.
In Rasch analysis, there is no need to delete incomplete data unless there is something wrong with the data that caused it to be incomplete.
You definitely need to equate the Q0 and Q1 analyses in some way.
Since you have both datasets, you could "stack" them so that the patients are in the data file twice. Then one analysis would give you the patient measures for both time-points in the same frame-of-reference.
Another possibility is that we have already collected and reported Q0. In this situation we would use the Q0 item and rating scale values (IFILE= and SFILE=) as anchor values for the Q1 analysis. Again we would have two measures for every patient.
In your situation, here are some obvious advantages to Rasch:
1. The patient samples can change
2. The QoL items can change (provided some remain items remain unchanged as common items - but even that can be relaxed with "vitual equating")
3. Missing data are allowed. If a patient is missing some observations, we can still estimate the patient's measure, but the S.E. of measurement will be bigger.
4. The floor-and-ceiling effects of raw scores are lessened, because Rasch straightens out the raw score ogive.
5. We can identify unusual response strings and item functioning. These may warn us of data entry mistakes, or help us diagnose patient symptoms, or identify malfunctioning items.
wlsherica:
Thank you for your reply, it's really helpful.
One more question, if there were some people loss of follow-up, it meas I only have their Q0 scores without their Q1 scores, should I input their Q0 data into my Q0 file, just analyze complete data?
Thanks again!!!
MikeLinacre:
Include everyone in Q0, Wisherica, unless there is some special feature of the people who do not have Q1 scores that will distort the Q0 measures for everyone else.
wlsherica:
Mike, thank you for your answer.
The special feature includes some patients died? Because I loss some patients
who departed this research, more than often that, some of them were dead.
I understand Rasch analysis could deal with missing value, however, this situation confuses me.
Thank you very much!!!
MikeLinacre:
This is a general problem in statistical analysis, wisherica. If our population changes between time-points, then we must verify that the change in population does not alter our inferences.
Look at the Q0 measures and fit statistics of the drop-outs. Are they a random sample of all Q0 measures and fit statistics? If so, their departure will not change our inferences. But if they are not a random sample (for instance, predominantly high or low performers, over-fitting or under-fitting), then we must evaluate their impact on our findings.
Here are several options (and you can probably think of more):
1. The drop-outs are a random sample of Q0. Their presence or absence does not change the findings. Analyze all the Q0 and Q1 that you have.
2. The drop-outs are skewing the Q0 findings. They should be dropped from Q0.
3. The drop-outs are skewing the Q1 findings. They should be assigned minimum (or maximum or random or the same as Q0 or ...) scores at Q1.
4. The drop-outs are a different class. Analyze Q0+Q1 without the drop-outs for one set of inferences: "What QoL motivates survival?". Analyze the Q0 drop-outs separately for a different set of inferences: "What QoL motivates demise?"
689. unidimensional by Winsteps??????
msamsa December 20th, 2009, 3:09pm:
Hello all,
what are procedures in order to know if the data is unidimensional by Winsteps?
As we know in SPSS, there is a clear procedure and calculations to verify the dimensions in the data. However, it seems to us inapprehensive way in Winsteps!
we want the steps and we need a help! ??)
wlsherica:
How about Winsteps manual?
connert:
In particular see:
https://www.winsteps.com/winman/index.htm?diagnosingmisfit.htm
Also the section in the manual entitled: "Multidimensionality - an example" Unfortunately the link in the online manual is wrong for this title.
690. Updates to SPSS
connert December 18th, 2009, 2:54pm:
I just updated SPSS from 17.0 to 18.0. To my dismay I found that any file that has been opened and saved using 18.0 cannot be read by Winsteps 3.68.1. Files opened and saved using 17.0 work fine. I can open and save the file with 17.0 that 18.0 has apparently changed and Winsteps then can read it. So I suggest that people not get the 18.0 upgrade for now until Mike has a chance to figure out the problem.
MikeLinacre:
Connert, are you talking about this bug in Winsteps when attempting to convert an SPSS file:
"SPSS Conversion failed. Line 18950 Error:5. Invalid procedure call or argument"
If so, it will be repaired in the next release of Winsteps.
691. RMSE
Raschmad December 6th, 2009, 6:50pm:
Are there any rules of thumb for interpereting RMSE and item and person estimates standard errors? Is an RMSE of 0.30 small enough to say that the measurement is precise?
Is RMSE expressed in logits?
Thanks
MikeLinacre:
The RMSE is expressed in logits, Raschmad, unless you have user-rescaled (USCALE= in Winsteps).
The RMSE for the persons is dominated by the number of items, and the RMSE for the items is dominated for the number of persons. The RMSE is a summary statistic which forms part of the Reliability and Separation indexes. So we usually look at those indexes to decide whether the RMSE is good enough for our purposes. If the samples of persons (or items) are what we want, then low reliability = high RMSE indicate that we need more items (or persons).
692. INESTIMABLE: HIGH
Raschmad December 6th, 2009, 10:35am:
Dear Mike,
I'm analyzing a multiple choice test.
For two items Winsteps has reported INESTIMABLE: HIGH. While the responses of individuals for these two items vary. All for options have been observed for these two items.
Why can't I get any statistics for them?
The other pint is the log likelihood chi square for the analysis is not significant. p=.3514.
Does this mean that data fits the model very well?
As far as I know this statistics should be significant which shows the data doesn’t fit the model.
Thanks
Anthony
Raschmad:
Sorry Mike,
That was a miskeying problem. I changed the key and both problmes were solved.
My appologies.
MikeLinacre:
Great result, Raschmad!
When the scoring key is incorrect, then the scored data can become almost random (like coin-tosses). These fit the Rasch model because they are like people of equal ability responding to items of equal difficulty. "Miskey cues": www.rasch.org/rmt/rmt54j.htm
693. Missing data
Raschmad December 4th, 2009, 7:35pm:
Dear Mike,
I have analysed a multiple-choice test which has some missing data with Winsteps.
I made the control file out of an SPSS file and analysed it with the command " CODES = 1234. " Then I deleted "." and analysed the data again with " CODES = 1234 "
The total scores of persons change and their measures also change as a result.
Can you please tell me which analysis is correct and why does this happen?
It’s a multiple-choice test and all the persons have tried all the items, there is no linking.
The model by default is PCM, " Groups =0 ". Should I change it?
Regards
Anthony
MikeLinacre:
Anthony: If this is a multiple choice test, then Winsteps expects a scoring key (the correct answers) specified with
KEY1 = 41343211324432213 (the correct responses to each item)
and also instructions what to do with invalid responses (missing data)
MISSING-SCORED = 0 (score invalid responses incorrect)
with these instructions, CODES = 1234. and CODES = 1234 produce the same scores and measures.
Since multiple choice items are dichotomies, GROUPS=0 does not apply, but, since it is specified, Winsteps will try to analyze the items as PCM. The difference will be that each item is reported separately in Table 3.2, and items with extreme scores (everyone succeeded on the item or everyone failed on the item) may not be estimated.
694. Unidimensionality
ashiqin October 12th, 2009, 12:33pm:
If I use MFRM with 3 facets, is it a must to check for unidimensionality of the items.
(I am constructing items for performance assessment)
How to determine the dimensionality of the items?
I read some of the research that used spss (PCA).
Or can I use WINSTEP? If I use WINSTEP, it will only be 2 facets.
MikeLinacre:
If your focus is on the unidimensionality of the items, Ashiqin, then you only need a two-facet analysis. This can be done with Winsteps.
Set up your data so that the items are the columns, and all the other facets are the rows.
You can see an example of this type of analysis in Example 15 of the Winsteps Manual. www.winsteps.com/winman/index.htm?example15.htm
Facets can output a two-facet output file suitable for analysis by Winsteps.
ashiqin:
Thank you very much Dr Linacre
ImogeneR:
Hello Dr Linacre and Ashquin,
I am trying to undertake this kind o f analysis also, but I don't understand what you meant by this comment, Mike:
"Facets can output a two-facet output file suitable for analysis by Winsteps."
How can I get this output? Which output are you referring to?
Many thanks
Imogene
ImogeneR:
Hi Again,
I've just been trying to run an analysis in winsteps using the 2 facet approach as per example in "exam15.txt" in winsteps. For some reason winsteps is saying "207 judges input" (correct) but only 5 measured. and it says 5493 appicants input (each applicant has 8 rows of scores so they appear 8 times, but there are only 686 individual IDs, so the extra '5' count seems to have gone on the rows of applicant data..or not. I am now confused. Control with data file attached - any illuminating comments would be most welcome!
Thanks
MikeLinacre:
Thank you for asking for our advice, Imogene.
A. In your Winsteps control file,
Please delete the "END LABELS" after your data.
B. Looking at your data, each data line is
5 character person id
then
5 ratings
so,
NI=207 is incorrect for this dataset,
NI=5 is correct for these data.
This suggests that these data are not the ones you intended to analyze.
There are 5488 data lines and 686 individual ids. 5488/6866 = 8.
This suggests that each correct data line should have 8 of the current data lines = 8x5 = 40 observations, with those observations located across the 207 judges, in a data matrix of 207x5 columns and 686 rows .
Does this help?
ImogeneR:
It does help thanks very much..but I am still a bit confused - wouldn't there be 1035 columns..because each judge will make 5 ratings for each applicant they see?
Therefore each applicant will have 40 ratings spaced out somewhere along a line that contains 1035 (207 * 5 ratings) ?
Sorry if I am not seeing the woods for trees! Also this would be an incredible restructure task of the data ..just wondering if there is another way of checking unidimensionality from FACETS output? Can I look at some output from FACETS in SPSS using prinicpal components analysis?
Thanks again
MikeLinacre:
Imogene, you are correct. I have edited my post.
It is not clear to me what you want Winsteps (or SPSS) to do, but as they both analyze rectangular datasets, you will need to reformat the Facets data file in some way.
Exam15.txt is reformatted from Facets:
columns = judges
rows = skater pairs x program x skill
So, if you want the same thing, then
columns = judges = 207 columns
rows = individuals x items = 686x5 = 3430 rows.
698. When to use many-facets Rasch model
s195404 November 23rd, 2009, 7:09am:
Dear Forum,
I am analysing a staff satisfaction survey and wonder whether to use Winsteps or Facets.
It seems to me that the work unit of a respondent may very well influence the probability of giving a certain rating to an item. In such a case, I would think that explicitly including work unit as a facet is the best approach.
Alternatively, I could consider work unit merely as a demographic variable (like sex) and check for bias through Winsteps.
I feel that these two approaches differ fundamentally in some ways, but that the outcome may not be noticeably different. What do others think? Thanks in advance.
Regards,
Andrew Ward
Brisbane, Australia
MikeLinacre:
Andrew, it sounds like respondents are only in one work unit, so Winsteps and Facets will give the same results. Easier is Winsteps. Put a work-unit code in the person labels, and then use PSUBTOT (Table 28) and DPF (Table 31) to investigate differences between work units.
s195404:
Thanks for this, Mike (as always) - it makes plenty of sense. When I tried Facets it was complaining about lack of connectivity which I guess is because the respondents only belong to a single work unit. The same will apply for geographic region and any other demographic characteristics.
Kindest regards,
Andrew Ward
s195404:
Actually, Mike, I've been thinking (mistake though it may be). I've seen examples where essay topics are treated as a facet. In such cases, I understand that each student chooses only a single topic. Does this mean that topic isn't really a facet, or that topics are connected through the rater facet?
Thanks again.
MikeLinacre:
"each student chooses only a single topic", Andrew. This means that a decision must be made:
1. The topics are equally difficult. Anchor the the elements of the topic-facet at the same value. You can then obtain fit statistics, and bias/interaction analysis for the topics. Group (but do not anchor) the students by topic, so that you can see the average ability of each student group.
2. The groups of students who responded to each topic are equally able (on average). Group-anchor the groups of students at the same value, and allow the topic difficulties to be estimated. You can then obtain fit statistics, and bias/interaction analysis for the topics.
699. 1PL
Raschmad November 21st, 2009, 7:36am:
Dear Mike,
Do persons with equal raw scores have equal ability measures under one parameter IRT?
Thanks
MikeLinacre:
Yes, equal raw scores on the same items = equal measures for 1PL.
In many other IRT models, the measures for the same raw scores are different. But this is too difficult to explain to examinees or to judges-and-juries in litigation. So for all IRT models, in practice, equal raw scores on the same items = equal measures.
700. anchor item parameters and step parameters
brightle November 20th, 2009, 7:25pm:
Hi Mike,
I am trying to examine raters' effects using a set of previously calibrated parameters as the anchor values.
the model has 3 facets, person, rater and item. We have all the persons' thetas and item parameters (thresholds and step parameters) estimated from a previous calibration.
The calibration worked when I fix the persons' ability and item threshold parameters, where the these two sets of parameters were not estimated and the anchor values were reported as the estimates.
However, when I added the constraints of item step values based on a previous calibration results, the program neglected the information and compute the parameters based on the current data. I tried several times and always got the same results. More specifically, both anchor values I input in the codes and the new set of values estimated based on the current sample were displayed in the output anchor file.
Could you please help to figure out how should I specify the anchor values in the model command?
Thanks.
Brightle
Below are the codes to fix both persons' ability parameters and item threshold and step parameters.
Facets=3
Title = experimental rater scores
Output = experimental_rater.out
score file = experimental_rater.sco
anchorfile=experimental_rater_ANC.txt
CSV=yes
Pt-biserial=yes
Convergence = 0, .01
Models = ?, ?, #, R4
Rating (or partial credit) scale=RS1,R4
1=1,0,A
2=2,-5.34,A
3=3,-.09,A
4=4,5.44,A
*
Rating (or partial credit) scale=RS2,R4
1=1,0,A
2=2,-5.06,A
3=3,-.58,A
4=4,5.65,A
*
Rating (or partial credit) scale=RS3,R4
1=1,0,A
2=2,-5.32,A
3=3,-.37,A
4=4,5.69,A
*
noncenter=2
labels=
1, person, A ; anchored
774,774,2.54
530,530,-2.74
563,563,-7.43
*
2, rater; the rater facet
1=r101
2=r102
3=r103
*
3, item, A; the item facet, the item facet is also anchored, using a previous calibration.
1=item1, .09
2=item2, .05
3=item3, -.14
MikeLinacre:
Brightie, thank you for your post.
Facets needs exact instructions to connect the rating scales to the models. Please replace:
Models = ?, ?, #, R4
by
Models =
?, ?, 1, RS1
?, ?, 2, RS2
?, ?, 3, RS3
*
brightle:
Hi, Mike,
Thanks for your quick reply and the comments. I made the relevant changes in the code, but still the same results.
Do you know other ways to get it fixed?
Thanks,
Brightle
MikeLinacre:
Brightie, please email me your Facets specification and data file so that I can investigate: facets -at- winsteps.com
701. Specifying item FACETs
ImogeneR November 16th, 2009, 11:54pm:
Hello
I need to specify the rating scale for an item FACET, where each if the items in a 12 station(item) clinical examination for medical students has a different number of total criteria. (ie max correct) .
How is it possible to specify this? through labels? I tried to follow the Knox cube example but go very confused!
Thanks
Imogene
MikeLinacre:
It sounds like there is one score for each item which is the "number of criteria correct".
Then:
Facets = 3 ; student, item, rater
Models =
?, 1, ?, R6 ; max score of 6 for item 1
?, 2, ?, R8 ; max score of 8 for item 2
...
?, 12, ?, R4 ; max score of 4 for item 12
*
Is this what you want, Imogene?
ImogeneR:
It worked a treat! First time..
Thanks!
702. Differential group functioning
ong June 24th, 2009, 4:30pm:
Dear Mike,
I am interested to find out whether when mathematical test items grouped in the curriculum content doamain (Calculation, numbers and number system, problem solving, space and shape and measure), do the boys or the girls find the bundle of items relatively easier ?
In the Winsteps manual, differential group functioning has been modelled as:
log(Pni1/Pni0) = Bgn - Dhi - Mgh
where
Bgn is the overall estimate from the main analysis of the ability of person n (who is in group DIF g)
Dhi is the overall estimate from the main analysis of the difficulty of item i (which is in DPF group h)
Mgh is the interaction (bias, DGF) for person group g on item group h. This is estimated from all persons in group g combined with all items in group h.
I have interpreted this as separate calibaration t-test approach at item-bundle level.
Attached here the output of my DGF analysis, after deleting 4 misfitting items and 148 persons with unexpected responses.
My questions:
(1) Will it be possible for winsteps to generate the fit statistics for bundle-level analysis (calculation, number and numbers systems, and etc) ? If yes, how could I do this?
(2) In the output, when the DGF contrast is positive, the t-value shown is negative. Why is that so? Is there any error in the way this analysis is conducted?
Do you have any references to any work conducted using this DGF feature in winsteps?
Thank you.
Regards,
Ong
MikeLinacre:
Thank you for your questions, Ong.
You asked: (1) Will it be possible for winsteps to generate the fit statistics for bundle-level analysis (calculation, number and numbers systems, and etc) ? If yes, how could I do this?
Reply: Sorry, I can't think of a straight-forward way of doing this with Winsteps, but with Facets you can report both the fit (assuming DGF=0) and the fit (assuming DGF=estimated value).
You asked: (2) In the output, when the DGF contrast is positive, the t-value shown is negative. Why is that so? Is there any error in the way this analysis is conducted?
Reply: thank your for reporting this bug. The numerical value of the t-value appears to be correct, but the sign is reversed in your output. I will correct this in the next release of Winsteps.
ong:
Dear Mike,
Thanks for the response.
I try running differential group functioning with facets. But I am not sure how to model the grouping of the items ( I have 52 items that I would like to group them to 5 groups : calculation, numbers and number system, problem solving, space and shape and measures).
I am able to run DIF for individual items.
Below are the codes that i used to analyse for individaul items. What should I add to these codes to run DGF? and the fit statistics?
Thank you
Regards,
Ong
Title= DIF analysis
Output=dif.txt ;name of output file
gstats=y
CSV=Y
Facets=3 ;3 facets (persons, items, Group=Gender
Arrange=2N,N,m,0f ;arrange tables in measure order, descending, etc
Positive=1 ;the scientists have greater ability with greater score
Non-centered=1 ;
Unexpected=2 ;report ratings if standardized residual >=|2|
Usort = U
Vertical=2N,3A,1* ;define rulers
Iterations=0
Barchart=yes
Model=?,?B,?B,R2
*
Labels= ;to name the components
1,persons ;name of first facet
1-2892=
*
2,gender
1=Boys
2=Girls
*
3,Items
1=ma1a
2=ma1b
3=ma2
4=ma3
5=ma4
6=ma5
7=ma11
8=ma13
9=ma14
10=ma15a
11=ma15b
12=ma16
13=ma17
14=ma22
15=ma24
16=ma25
17=mb1
18=mb2
19=mb3
20=mb4
21=mb6
22=mb7
23=mb9a
24=mb9b
25=mb11
26=mb13
27=mb14
28=mb16
29=mb18
30=mb19
31=mb24
32=mb25
33=m1
34=m2
35=m3
36=m4
37=m5
38=m6
39=m7
40=m8
41=m9
42=m10
43=m11
44=m12
45=m13
46=m14
47=m15
48=m16
49=m17
50=m18
51=m19
52=m20
MikeLinacre:
Thank you for your question, Ong.
You write: "I have 52 items that I would like to group them to 5 groups : calculation, numbers and number system, problem solving, space and shape and measures".
Please do:
A. put a code at the start of the item label showing what group the item is in.
We will use this for a reference in the data.
B.. put a group number after the item label showing what group the item is in.
We will use this for subtotals of item difficulty by item type.
For instance, suppose that item 1, is in group 1, calculation:
3,Items
1=c-ma1a, , 1 ; c for calculation and 1 for item group 1.
C. Define facet 4 for the 5 types of item,
We will use this to look for interactions, and to produce summary fit statistics by item-group:
Labels=
....
*
4, item type, A ; anchor this facet at zero. It is a dummy facet.
1 = c-Calculation, 0 ; use the same code letter as in the item label
2 =
...
*
D. Change the model to 4 facets with gender x item group interactions:
Facets=4 ;4 facets: persons, Group=Gender, items, item type
Model=
?,?B,?B,?,R2 ; igender by items interactions
?,?B,?,?B,R2 ; gender by item type interactions
*
E. Tell facets where to find the information for facet 4:
Dvalues=
4, 3, 1, 1 ; the elements of Facet 4 (item type) are referenced by the code letter at the start of the element labels in facet 3 (items)
*
F. The easy part! Do not change the data file.
OK?
ong:
Dear Mike,
Thank you for the explanation and the codes to run DGF with facets. I hope I have interpreted your explanation and codes correctly.
I have made modification to the codes and I have posted at the end of this message.
However, when I compare facets output with the winsteps output, the results seem different especially the t value and the probability.
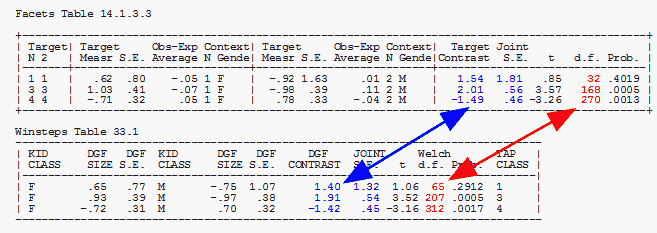
Attached here snapshots of Table 13.1.1 and Table 13.1.2 of facets analyses and Table 30.1. and table 33.1 of winsteps analyses.
Why are there differences in the results when using these 2 software analysing the same data?
Thank you.
Regards,
Ong
Here are the codes for the facets analysis:
Title= DIF analysis pretest
Output=pre1.txt ;name of output file
gstats=y
CSV=Y
Facets=4 ;4 facets (persons,Group=Gender,items,item type
Arrange=2N,N,m,0f ;arrange tables in measure order, descending, etc
Positive=1 ;the scientists have greater ability with greater score
Non-centered=1 ;
Unexpected=2 ;report ratings if standardized residual >=|2|
Usort = U
Vertical=2N,3A,1* ;define rulers
Iterations=0
Barchart=yes
Model=
?,?B,?B,?,D; gender by item interactions
?,?B,?,?B,D; gender by type interactions
*
Labels= ;to name the components
1,persons ;name of first facet
1-892=
*
2,gender
1=Boys
2=Girls
*
3,Items
1=c-ma1a,1
2=c-ma1b,1
3=c-ma2,1
4=s-ma3,4
5=m-ma4,5
6=p-ma5,3
7=c-ma11,1
8=n-ma13,2
9=m-ma14,5
10=p-ma15a,3
11=p-ma15b,3
12=n-ma16,2
13=s-ma17,4
14=s-ma22,4
15=n-ma24,2
16=s-ma25,4
17=n-mb1,2
18=s-mb2,4
19=c-mb3,1
20=m-mb4,5
21=p-mb6,3
22=p-mb7,3
23=p-mb9a,3
24=p-mb9b,3
25=n-mb11,2
26=p-mb13,3
27=s-mb14,4
28=m-mb16,5
29=n-mb18,2
30=c-mb19,1
31=p-mb24,3
32=n-mb25,2
33=c-m1,1
34=c-m2,1
35=c-m3,1
36=n-m4,2
37=n-m5,2
38=c-m6,1
39=n-m7,2
40=c-m8,1
41=c-m9,1
42=m-m10,5
43=n-m11,2
44=s-m12,4
45=p-m13,3
46=s-m14,4
47=p-m15,3
48=c-m16,1
49=p-m17,3
50=c-m18,1
51=c-m19,1
52=m-m20,5
*
4, item type, A ; anchor this facet at zero. It is a dummy facet.
1 = c-Calculation,0; use the same code letter as in the item label
2 = n-Numbers and number system,0 ;
3 = p-problem solving,0;
4 = s-space and shape,0;
5 = m-measures,0;
*
Dvalues=
4, 3, 1, 1 ; the elements of Facet 4 (item type) are referenced by the code letter at the start of the element labels in facet 3 (items)
MikeLinacre:
Ong, this Facets analysis appears to be under-constrained. Does it reports "subsets"?
Perhaps this is needed:
2,gender,A ; dummy facet for interactions, anchored at 0.
1=Boys,0
2=Girls,0
*
ong:
Dear Mike,
To model gender and domain interaction to study bias, I conducted a DGF analysis with winsteps 3.68 and another analysis with minifac 3.65.
It seems that there is a large difference in the s.e using these two different softwares.
Conceptually is DGF the same as the interaction of gender and domain in Facets analysis?
Why is there a large difference in the s.e estimated?
Attached here the output from both anlyses.
Thank you.
Regards,
Ong
MikeLinacre:
Thank you for your question. Ong.
I performed the computation with the KCT data.
The person and item estimates are almost identical for Winsteps and Facets.
Inspecting these results, the DGF Contrast and Joint S.E. are comparable, but the degrees of freedom do not agree. The Facets number is correct. Winsteps is incorrect. It includes some extreme scores in its computation. This bug will be repaired in the next update. In Winsteps, use PDFILE= and IDFILE= to remove all extreme persons and items before computing DGF.
Tightening the convergence criteria for both Winsteps and Facets will probably bring the two analyses into closer alignment.
ong:
Dear Mike,
Thanks for the response and insight.
You mentioned that "tightening the convergence criteria for both winsteps and Facets will probably bring the two analyses into closer alignment".
I am not sure what you mean by this.
What command do i need to write to run as you suggest?
Thank you.
Regards,
Ong
MikeLinacre:
Ong:
The convergence criteria in Winsteps are set with:
CONVERGE=
LCONV=
RCONV=
and in Facets with
Converge=
Set the values smaller for tighter (more exact) estimation convergence.
ong:
Dear Mike,
You mentioned in the previous post that you can't think of a straight forward way to generate the fit statistics for "item-bundle" using DGF.
Does it make sense to use the command ISUBTOTAL to generate the fit statistics for item-bundle? How does WINSTEPS compute the fit statistics of item-bundle using the ISUBTOTAL command?
When we use the command to run DGF, how does WINSTEPS compute the DGF size for each group menbership?
Does it find the average of the item difficulty in the item-bundle for each group membership?
Thank you.
Regards,
Ong
MikeLinacre:
Ong:
ISUBTOTAL= does not recompute underlying values. It produces the same summary statistics as Table 3, but for a subset of items.
DGF= uses the response residuals from the main analysis to estimate the size of the interaction between a group of items and a group of persons. The essential formula is:
Size of DGF = (sum of relevant residuals from the main analysis) / (sum of model variance of relevant observations from the main analysis).
There is no averaging of item difficulties.
ong:
Dear Mike,
Thank you for the response.
I hope I have interpreted this correctly, ISUBTOTAL produces the same summary statistics as Table 3.
I have 20 items, which are grouped into 3 groups consisting of 3, 12 and 5 items respectively.
And this is reported in Table 27.4-Table 27.6.
If I look at group 1, a group consisting of 3 items, the Infit MNSQ is 0.99 and Outfit MNSQ is 1.08, then I would interpret the fit statistics for items grouped in group 1 as 0.99(Infit) and 1.08(outfit) respectively.
Hence, this would represent the fit statistics for this bundle of items.
Is this the way you would interpret it?
Attached here the output.
Thank you.
Regards,
Ong
MikeLinacre:
Ong:
You write:
"Hence, this would represent the fit statistics for this bundle of items."
Table 27 shows the average fit of the items in the bundle. This is not the same as the overall fit of a bundle of items - but it would usually be close.
703. Observed scores, recoding, and calibration
JCS November 11th, 2009, 3:25pm:
Hi Mike,
Operationally, we collect two raters' holistic scores (1-4) on a single essay (in addition to MC questions). The reported score is a weighted combination of the essay (.35) and the MC items (.65) scaled to 200-800. The final essay score is the average of the two rater scores--with usual steps taken if separated by more than one point. So, our final range of essay scores for each examinee is 1, 1.5, 2, 2.5, 3, 3.5, and 4 (=7 categories). We want to use the PCM with this essay item (dichotomous Rasch with MC items). It was suggested to us that we calibrate the essay item using only the first raters' scores as they are considered randomly equivalent to the other raters. I should also mention that we're using pretest data to calibrate only. The item parameter estimates will be used for scoring the operational data later.Here are my questions:
1) Is it necessary to include the weights (.35 & .65) in the calibration? Or just the scoring?
2) If we only use the first raters' scores then we only get 3 thresholds for this item. Don't we need 6 if the final scores are as noted above?
3) If the suggestion to use only one of the raters scores is accurate, how should I recode the final scores? During calibration, the scores are 1-4. But during scoring they'd be 1 to 7.
4) Doesn't it make more sense to calibrate using the final scores (recoded to 1-7 instead of 1, 1.5, 2,...,4? It seems to me this would make scoring easier.
5) Lastly, examinees who score less than 2 on the essay (using the average of the two rater scores) fail the test and don't receive any score. Thus, we'll never see scores of 1 or 1.5 operationally. Should we include these values in the calibration?
I know other testing operations have similar situations as this but it's so hard to determine best practices b/c technical manuals are often lacking!
Thanks!
-JCS
MikeLinacre:
Thank you for your post, JCS.
1) First analyze the data without the weighting to verify that all is correct.
Then include the weighting in order to obtain measures in the weighted context. Weighting distorts fit statistics, reliabilities, etc., so report fit and reliability from the unweighted analysis.
2) The rationale for using only one rater's score is not clear to me. You could either: 1. Model 2 raters: this can be implemented in Facets
or: 2. Use the summed ratings in your PCM in the "first" unweighted analysis, and then use an essay weight of (.175) in the second weighted analysis.
3) This procedure is strange, but here is an approach.
a) Do the unweighted 1-4 analysis to verify fit etc.
b) Do the weighted 1-4 fit analysis (essay weighting is .7): obtain person measures.
c) Anchor (fix) the person measures. Do the weighted analysis with 1-7 data (essay weighting is .35). Obtain item difficulties and PCM thresholds.
d) Unanchor person measures. In the weighted analysis (essay weight .35), anchor item difficulties and PCM thresholds, obtain final measures for the persons, and the score-to-measure table for later use.
4) Since the scores are weighted, 1, 1.5, 2,...,4 at weight .35 is the same as 1-7 at .175. So the easier scoring makes sense.
5) If categories are not observed, then they cannot be calibrated. But, because of the weighting in this design, unobserved categories will cause problems. Please include some dummy person records which look like what low performances would be. Omit these from your final reporting.
OK?
JCS:
Thanks, Mike. Here's a little more detail about using one instead of two raters. The ratings are very highly correlated so including both is similar to having two items that measure the exact same thing. To clarify, the suggestion was to calibrate using tryout data (which includes essay scores from the full scale, 1-4) but use only the first raters' data. Now we'd have the item parameter estimates for operational scoring (from actual test-takers). We could use the essay item estimates (difficulty and thresholds) obtained from the calibration and score both rater's scores. We would simply apply the estimates to both scores, but weight each score using .5. This should cover all integer and fractional scores.
After posting my original questions I remembered that the averaged categories of 1.5, 2.5, and 3.5 result in probability category curves that are too small and thus some type of collapsing of categories would be needed, I think.
I hope this clarifies but it brings up another question of how to apply both the .65/.35 weights and the .5/.5 weights simultaneously.
MikeLinacre:
JCS,
How to combine the .65/.35 weights and the .5/.5 weights?
Write down an imaginary response string for a test-taker. Then compute for each response its weight in the test-taker's final raw-score.
Compute the range of possible weighted raw scores. Does this make sense? If not, adjust the weights up or down accordingly.
The final set of weights is used in the Models= specifications corresponding to the responses.
Also, when we average ratings like these (1,1.5,2...) then we expect to have low-frequency categories at 1.5, 2.5, ... because we expect the raters to almost-always agree. The low-frequency categories do not contradict our theory about the meaning of the rating scale, and so do not need to be collapsed. We collapse categories when a low-frequency category contradicts the meaning of the rating scale. For instance, on a Likert "agreement" scale, if we observed that SD, D, N, SA all are high frequency categories, but A is a low frequency category, then we would diagnose a malfunction of the rating scale and take remedial action about A.
704. test translation
RaschNovice October 29th, 2009, 2:58pm:
we want to develop a translation of a scale of self esteem. we have 200 english speaking subjects and 200 spanish speaking subjects. The test is 25 items.
Which approach is better?
Approach 1) The difficulty levels of the items are compared across samples.
Approach 2) Many of our subjects are fluent in both languages. This means some subjects could take both instruments. This would seem to be a stronger approach, but how to do the analysis? Usually, it's that two tests are equated by common items. Here, is a common sample of persons that links the items. Is this approach okay, does it make sense?
RaschNovice
MikeLinacre:
Thank you for your questions, RaschNovice.
Approach 1 should be a finding from an equating study, not an assumption instead of one.
Approach 2 - yes. This is "common person equating". Organize your test administraction so that half the subjects see the Spanish instrument first, and half the subjects see the English instrument first.
Google "common person equating" to see many examples.
ong:
Hi Raschnovice,
You can look into differential item functioning.
This article might be of interest to you.
Ong, S. L., & Sireci, S. G. (2008). Using bilingual students to link and evaluate different language versions of an exam. US-China Education Review, 5(11), 37-46.
It is available in ERIC database.
Regards,
Ong
PS: I am not the author of the article, just the same surname.
Tristan:
Hi All,
How can I post a new thread?
Thanks
MikeLinacre:
Tristan, click on "Rasch on the Run", then the "new thread button"
The link is https://www.winsteps.com/cgi-local/forum/Blah.pl?b-cc/
705. Single score, multiple latent variables
connert October 28th, 2009, 11:31pm:
This obviously is related to my most recent question. If you have an instrument that is administered to a single sample and the items divide into subsets corresponding to correlated but theoretically different latent variables, is there a way to produce a single overall score that still preserves basic measurement properties? The prototypical example of this seems to be an "achievement" test with subtests in math, reading, and written expression. In my case it is a rating system for "fidelity" in the use of a therapy system which, on empirical grounds, has three clumps of items that all scale very well by Rasch criteria but do not work as a single group of items (there are multiple items with MSQ's that are very high).
MikeLinacre:
Connert, this is the same problem as combining height and weight in a physical situation.
A general solution is to cross-plot height against weight. The slope of the line of commonality gives the best conversion between height and weight, and also the best coefficients for combining them into one number.
If the line of commonality indicates that weight = height*2 (in general), then the best combination is: (w + h*2)
706. Analyzing Medical Records Archives
connert October 26th, 2009, 12:26am:
I have access to a large data base of medical records from elderly persons presenting in emergency departments of hospitals in the US. The question is whether a Rasch measure of physical and cognitive disability can be constructed from these records with the aim of improving treatment recommendations (esp., return home or, stay in the hospital) and avoiding bad outcomes. The records contain a variety of kinds of "items". Some may be quantitative measures like temperature, blood pressure, and the like. Others may be ranked categories of various kinds, such as experiences dizziness or not or cannot get out of a chair without help. These ratings and measurements are likely made by different but unidentified people. My question is, how do I approach this? What kinds of models would be appropriate? Is this even possible? What questions do I need to be asking? Any help or suggestions would be welcome.
MikeLinacre:
Yes, Tim. You have encountered a familiar situation. Survey questions are often compiled without well-defined latent variables in mind. It is difficult to recover meaningful latent variables from them. But here are some steps:
1. Transform all the clinical etc. variables (items) into ordinal categories in which, generally speaking, higher category = better health. 5 categories for each variable (or less) are enough at this stage. Don't worry about losing useful information at this stage, you can always go back and recategorize into finer gradations.
2. Classify the variables roughly into different content areas.
3. Choose a small set of items which appear to be central to a latent variable in a content area.
4. Rasch-analyze the content area: weight the central items at 1. The other items at 0. Use the partial-credit model (ISGROUPS=0 in Winsteps).
5. Items with mean-squares less than 1.5 are probably loading on the latent variable.
6. Redo the analysis reweighting so that those items are weighted 1 and the other items weighted 0.
7. This analysis usually confirms which items belong to this latent variable. Then you can move on to the next latent variable.
Unfortunately, usually only a fraction of the items can be assigned to latent variables. But something is better than nothing!
seol:
Dear Dr. Linacre
I have a quick question about your suggestions above.
weight the central items at 1. The other items at 0.
Why do we weight core items like this above? what's the difference, if not, in Rasch analysis?
Thanks in advance
Seol
MikeLinacre:
Seol, we have a core of items (weight 1). We wonder if any other items also belong to the core. So we weight all the other items at 0. The 0-weight prevents those items from altering 1) the measures and fit of the persons, and 2) the measues and fit of the core items.
But the 0-weight items do have measures and fit statistics. If any of those 0-weight items fit with the core items, then those items can be made 1-weight items, and so added to the core.
connert:
That was a very helpful answer. Thank you.
707. beginnerhelp
6sri5 October 9th, 2009, 6:43am:
Hi everyone
I am a complete novice of rasch analysis. could some one suggest to me introductory texts on rasch analysis. Though it is too early I was also wondering whether any one could suggest a software so that I could learn by analysing.
Thanks in advance
seol:
Bond T.G., & Fox, C. M.(2007). Applying the Rasch model:Fundamaental measurement in the human sciences. Lawrence Erlbaum Associates.
Oh.. I forgot... WINSTEPS and Facets computer program(https://www.winsteps.com) for Rasch analysis might be helpful for you.
MikeLinacre:
6rsi5, there is considerable introductory printed material about Rasch analysis, free to download, at https://www.rasch.org/memos.htm
There is also a large selection of free and paid Rasch software at https://www.winsteps.com/rasch.htm
wlsherica:
I'd like recommend �uBond T.G., & Fox, C. M.(2007). Applying the Rasch model:Fundamaental measurement in the human sciences. Lawrence Erlbaum Associates.�v,too. This one is really easy to understand!!!
connert:
The 2007 edition of Bond and Fox comes with software on a CD.
wlsherica:
Lovely news!!!
708. Rasch and political analysis
ary October 8th, 2009, 5:08pm:
Hi Mike ;)
Really need some good advice...
how can i best answer and convinced my friend intellectually ;D that rasch analysis is also applicable and a better tool in analyzing political issues/election procedures? i.e. political inclination. hierarchical order of contributing factors in determining a success/failure of a political party....
Does anyone have good papers on the application of rasch in the field of political science? Is there any instrument related to this issue that are being developed through rasch anaysis? I really appreciate any help.
ary
MikeLinacre:
Ary, your problem sounds to be the type that Pedro Alvarez at the University of Extremadura in Spain would investigate. He is an economist who delights in finding new or unusual applications of Rasch measurement. You can find some of his papers through Google Scholar.
ary:
TQ mike!
709. separation and strata
ashiqin October 12th, 2009, 12:17pm:
Dr Linacre. This is a very simple question but I am not sure of the difference of separation and strata.
Separation = This estimates the number of statistically distinguishable levels of performance in a normally distributed sample with the same "true S.D." as the empirical sample, when the tails of the normal distribution are modeled as due to measurement error.
Strata = This estimates the number of statistically distinguishable levels of performance in a normally distributed sample with the same "true S.D." as the empirical sample, when the tails of the normal distribution are modeled as extreme "true" levels of performance.
If I want to report the number of statistically distinguishable levels of performance. Which one should I use.
May be I don't really understand between measurement error and extreme true level of performance.
MikeLinacre:
Ashiqin, think about the distribution of your person measures.
There are persons at each extreme end of the person distribution.
Why are those persons at the extremes?
Are those persons are at the extremes because they are definitely performing higher (or lower) than the other persons? If so, report the Strata.
Are those persons are at the extremes because they obtained higher (or lower) scores by accident (guessing, carelessness, luck, special knowledge, ....), then report Separation.
If you don't know which to report, then report Separation. Then you will not mislead yourself (or others) into thinking that your test discriminates more levels of performance than it actually does.
ashiqin:
Thank you Dr. Linacre,
It really helps- :)
710. Examine group difference
Hyun_J_Kim October 12th, 2009, 5:09pm:
Hello,
I'd like to use a many-facet Rasch measurement model for my disseration study.
To briefly talk about the context, nine raters (three novice, three developing, three expert raters) will score 18 examinees' speaking responses using an analytic scoring rubric across three times. In other words, the raters will score six responses each time, making 18 in total. Different sets of responses used for three different occasions are assumed to be equivalent. Since the raters will use an analytic rubric, each spoken response will receive five component scores.
What I'd like to examine using a many-facet Rasch measurement model is (1) to what extent three rater groups are different in their rating ability at each scoring point and (2) how each group develops their rating ability over time. In the study, I define rating ability in terms of accuracy of scoring. That is, raters' ability are determined upon the degrees they are internally consistent and interact with respect to the examinee ability and the rating criteria. Also, their use of scoring criteria will be qualitatively examined along with the Rasch analysis to decide their accurary of scoring. For the analysis, I plan to include five facets: examinees, items (analytic rating scores), raters, rater group, rating criteria.
My questions are:
1) I'll refer to the rater group facet to compare three groups' sevirity in rating. Then, in order to compare each group's severity across three different times, can I simply compare logits from three different output files after running the program each time the raters score six responses?
Also, for the comparison of internal consistency and bias, is it possible to compare logits obtained from three different outputs?
If not possible, what do I need to do to compare three groups across three times?
2) Although I compare logits, I cannot conclude whether the groups are statistically different or not. Is there any way to tell more statistically how different the groups are in terms of internal consistency and bias using the Rasch analysis?
I'd really appreciate any response or suggestion.
Thank you.
MikeLinacre:
Alasgawna, thank you for your questions about many-facet Rasch measurement.
From your description, it sounds like everything you need can be obtained from one analysis of all the data. But, you do need to be exact about specifying your measurement model.
You can model a group effect at each time-point. This will have a standard error, so you can do a t-test to see if the group has changed statistically significantly.
You also need to define what "bias" is. Then you can model it as a change in measures or misfit-statistics.
There are many other possibilities. But you do need to be exact and specific about the hypotheses you want to investigate. Once you have defined your hypotheses exactly, the analysis is usually straight-forward conceptually.
711. Adjust a Likert Result Through Polytomous Rasch Mo
lonb October 5th, 2009, 8:46pm:
Hey all - I'm a stats novice and a software expert. I'm working on a product rating / review system for my company. We receive Likert data as reviews about products (zero through five stars). Once I have the full set of reviews, I'd like to adjust for bias in the data through the polytomous Rasch model.
I understand (to some degree) how if I pass a given rating (x) into the model, and the info about the rating scale (max value, etc.), the model will calculate the probability of the rating at any given threshold.
What I'd like to do is adjust the entire data set in aggregate, in a weighted-like manner. So if in the raw data a product has ten votes as "1"; the outcome data has 10 votes as "1", 5 votes as "2", 1 vote as "3", etc. Similarly, raw data with 20 votes as "2"; outcome data would have 10 votes as "1", 20 votes as "2", 10 votes as "3", 5 votes as "4", and 1 vote as "5". and so on.
Could anyone here help prepare a formula to do this?
Or, just provide feedback about this approach?
Thanks!
- Lon
MikeLinacre:
Your approach to Likert date is new to me, Lon.
You write: "adjust for bias". Could you be more specific about the nature of the bias?
In general, we can estimate the parameters of a Rasch model from the original data. Then we can adjust the parameters in whatever way we like. Finally we can simulate a new dataset based on the adjusted paramaters. Is this what you are thinking of, Lon?
lonb:
Mike - Thanks for the reply! I think the biases we face are the same (or at least similar) as any ratings scale, such as central tendency, acquiescence, etc.
I'm not sure what you mean by "estimate the parameters of a Rasch model"... I would think that if I wrote the ratings scale and have a data set, that should be the complete set of parameters, or at least any other necessary parameters (statistical in nature) could be calculated?
However, in the end, your comment about simulating a new dataset: yes that is exactly what I'm looking for. How can we do this?
Thanks again,
Lon
MikeLinacre:
Now you have set us a challenge, Lon.
Estimating Rasch parameters from the original data is usually straight-forward.
Computing probabilities from those Rasch parameters and simulating data is usually straight-forward.
But adjusting for central tendency, acquiescence, etc. is difficult. In fact, I don't know how to do it. Perhaps someone else on this Forum knows ....
lonb:
THis does a good job explaining how, and provides a starting point for a formula:
http://en.wikipedia.org/wiki/Polytomous_Rasch_model
MikeLinacre:
Lon, Yes. That Wikipedia page describes the polytomous Rasch model, but unfortunately it does not explain how to adjust for those biases (central tendency, etc.)
lonb:
The formula provided accounts for those biases.
seol:
Dear lonb
Could you explain briefly how to adjust rater effect(ex, central tendancy, restriction-of-range effct) with polytomous rasch model? although I don't think so....except MFRM model...
MikeLinacre:
Lon, a standard polytomous Rasch model adjusts for item easiness/difficulty and person leniency/severity, but not for more subtle aspects of person misbehavior, such as halo effect, central tendency, response sets, etc.
For these we need a methodology to apply to the data:
1. How do we recognize the bias exists in the data?
2. How do we adjust the ratings of an individual person to compensate for the bias?
3. How do we automate the adjustment so that it can be applied to all individuals on a routine basis?
Lon, the second step is the most challenging. For instance, we can recognize a response-set (someone selecting option A every time), and, if we know how to adjust for it, we can automate the adjustment. But what is the adjustment for a response set, other than omitting the person?
712. Displaying Likert Data
DAL October 5th, 2009, 3:36pm:
Dear Dr Linacre,
I am comparing Likert Scale data as analysed by winsteps to traditional methods.
I'm trying to put the data from table 2.14 into an excel bar chart so I can compare it to a chart that I did based on aggregating the raw data. Is there any place I can find a table of these figures? I've looked but couldn't find anything that resembled them.
Secondly, the graph on P115 of 2nd Edition of Bond & Fox would be an ideal graphic, but I believe unavailable on winsteps (at least as at 3.66). There are some similar graphs at 12.5 & 12.6, but they are to my untutored eye, harder to make sense of. I'm sure you have a lot of requests for things to include in winsteps, but I wonder if there is the slightest chance that something similar might be considered.... ?
Please excuse my ignorance on these matters,
regards
MikeLinacre:
Thank you for these requests, DAL.
The numbers required for Table 2.14 may be in the output file produced by ISFILE=
Displaying the functioning of polytomous items is a challenge. That is why there are so many sub-tables in Tables 2 and 12.
B&F Figure 6.3 (p. 115) shows the items in columns. Winsteps Tables 12.5, 12.6 show the categories in columns. This works better for long tests, but I will add your request to the Winsteps wish-list for short tests.
Also, B&F Figure 6.3 (p. 115) shows the Rasch-Andrich thresholds for the items. These are difficult to conceptualize because they are disordered. This misleads our eyes into seeing the categories as disordered. "Disordering" means "low category frequency", not "incorrect category numbering". Consequently Winsteps does not show this display in Table 12. But the Rasch-Andrich thresholds for the items are shown in Table 2.4, 2.14 as you have discovered.
DAL:
Thanks, ISFILE works a treat!
713. Guidelines for Item Discrimination
connert October 5th, 2009, 3:01pm:
Are there guidelines for values of estimated item discrimination for survey attitude items? When is item discrimination too low or too high? Should they be distributed in some known way?
Thanks,
Tom
MikeLinacre:
Connert, in Rasch equations, the modeled item discrimination is 1.0
Empirical item discriminations in the range 0.5 to 1.5 usually give reasonable fit to the Rasch model. Always be concerned about low discriminations before high discriminations.
Sorry, I can't recall any research into the Rasch-model predicted distribution of empirical discriminations.
714. Single Essay
JCS October 2nd, 2009, 3:31pm:
Dr. Linacre,
I have a testing situation in which each candidate responds to only one of 21 different essay prompts (the candidate is only given one--so they don't have the choice of prompt). Each essay is scored holistically by two raters. Every rater rates every prompt and every rater is matched with every other rater.
Is it possible to use Facets despite the fact that candidates respond to only one item?
Many thanks!
MikeLinacre:
JCS, to analyze these data (actually using any method), you have to make some assumptions about the essays. The two most common assumptions are:
1. The essays are equally difficult. (In Facets, anchor them all at the same measure)
or
2. The sub-samples of candidates responding to each prompt are equally competent on average, i.e., random equivalence. (in Facets, group-anchor the candidates administered each essay at the same value.)
A good approach is to try both approaches and see which set of measures makes the most sense.
715. Anchorfile and facets interaction
ImogeneR September 28th, 2009, 4:34am:
My experiments indicate that, in most situations, the "variance explained" in the data is proportional to the variance of the element measures in the facet.
So we can:
Hi Nike, my colleague Chris Roberts and I are trying to isolate rater*candidate and rater*item variance out of the 68% or 'residual' variance left over after running a facets analysis of rater/item/candidate. (no 2 raters saw same candidate on same question so we can't use bias tables I think)
Chris got these isntructions from you via email:
1. Do a Facets analysis for main effects: persons, items, raters.
2. Anchor the main effects (anchorfile=) and do a Facets analysis for the interaction effects:
person*rater (disposition of rater towards person)
person*item (context specificity)
rater*item (rater item stringency)
3. The person*rater* item (residual error) will be the residual variance after 2.
My question is, I tried this, but got exactly the same results in table 5.0 as before (ie 31% explained by rasch measure, the rest residual.
Am I doing some thing wrong with teh anchor file? Do I need to change model statments? I notice with the anchorfile as specification file there seems to be a model statement for every combination?
many thanks for your help as always.
Imogene
MikeLinacre:
Imogene, your design will work, but you need to change the model statements and the facets at step 2. It is easier to model everything and omit the facets at step 1.
Example:
Facets = 6 ; person, item, rater, person*rater, person*item, rater*item
Step 1:
Model = ?,?,?,X,X,X,R
Step 2: use anchor file values from step 1 for facets 1-3, and the rating scale.
Model = ?,?,?,?,?,?,R
OK?
ImogeneR:
Thanks very much Mike. I tried Step 1..but now I keep getting the attached error..even though there are definitely 5 columns of ratings..it would appear that I can't get facets to realise the X statements in the Model = should not be counted?
It seems to be reading the first 6 columns across as facets?
APologies for taking up your time if I am missing something basic..I looked through the examples in Help..but I can't seem to resolve it.
Kind regards
Imogene
MikeLinacre:
Imogene, there are 6 facets, so we we need 6 element numbers for each observation.
Example:
Facets = 6 ; person, item, rater, person*rater, person*item, rater*item
Model = ?,?,?,X,X,X,R
Labels=
1, Person
1, person 1
...
*
2, Item
1, Item 1
...
*
3, Rater
1, Rater 1
...
*
4, person*rater
1, person*rater 1 ; use Excel to construct these numbers
...
*
5, person*item
1, person*item 1
...
*
6, rater*item
1, rater*item 1
*
So each observation will have its own data line, for example:
1 , 4, 3, 6, 12, 7, 3
ImogeneR:
Ok , I think I am, lost ... I'm sorry if this is a silly question, but I'm not really sure what exactly I am constructing in the new facets, in the context of teh data file!
if I construct those numbers in Excel, my thought is I am essentially just concatenating or multiplying the labels for 2 elements involved in each interaction to come up with a new unique number...it's a label..the facet doesn't have any value then as such? ie There is no rater*person observed score without the item..
eg if rater 1 is 66021 and person 1 is 66524 then person*rater becomes 6652466021..it's just a column of numbers (which I've noted from my first try get too big for the integers allowed in Facets..)
Please feel free to refer me to a text if I am missing something basic..
MikeLinacre:
Imogene: yes you have the right idea.
But all you need is a unique number for each interaction term.
It is unlikely that you have 66021 raters, so you can use Excel to renumber them from 100 (or another convenient number), and use the number 66021 in the rater label.
ImogeneR:
Thanks so much I will have another go!
716. Dimensionality Problem
PsychRasch September 24th, 2009, 5:50pm:
Hello community
I want to ask if always fits are lower than zero there's a local change in the intensity of the dimension.
PsychRasch:
Also I have this Table, please help me with the interpretation:
CONTRAST 1 FROM PRINCIPAL COMPONENT ANALYSIS OF
Table of STANDARDIZED RESIDUAL variance (in Eigenvalue units)
-- Empirical -- Modeled
Total raw variance in observations = 48.2 100.0% 100.0%
Raw variance explained by measures = 21.2 44.0% 42.1%
Raw variance explained by persons = 6.2 12.9% 12.4%
Raw Variance explained by items = 15.0 31.1% 29.7%
Raw unexplained variance (total) = 27.0 56.0% 100.0% 57.9%
Unexplned variance in 1st contrast = 3.1 6.4% 11.5%
PsychRasch:
I don't think there's a second dimension, but my master think there are three more dimensions. INFIT Values are < 1.
| 1 | .73 | -.46 .79 .25 |A 14 r22 |
| 1 | .72 | -.29 .81 .30 |B 13 r21 |
| 1 | .48 | .34 .57 .25 |C 9 r17 |
| 1 | .40 | -.64 .93 .63 |D 10 r18
I emphasized the infits. These are items of the first contrast.
MikeLinacre:
PsychRasch, infit values less than 1.0 indicate better fit of the data to the Rasch model than the Rasch model predicts. This could be an indication of local dependency in the data, but not an indication of dimensionality.
Your "Unexplned variance in 1st contrast" has an eigenvalue of 3.1 (the strength of 3 items). This is greater than 2.0 (the highest value expected by chance), so there may be off-dimensional behavior in your data.
Since the off-dimensional behavior is probably not in the items coded A,B,C,D in your output, it is probably the items coded a,b,c,d.
The meaning of Table 23.3 is in the contrast between items A,B,C,D, and items a,b,c,d
PsychRasch:
Many thanks Professor Linacre
English is not my mother language. Can you explain me a little more about the meaning of "off dimensional"?
Thank you
MikeLinacre:
PsychRasch:
"off dimensional" means "something in the data that contradicts the Rasch dimension".
For example, in a math test, off-dimensional aspects of the data could be
guessing, carelessness, data entry errors, an incorrect answer key, a "reading" dimension.
PsychRasch:
Dr. Linacre
Many many many thanks!! :)
PsychRasch:
Good day Dr. Linacre
This is another extract of Table 23.3, where it show items marked as a, b, c. According to results, item d has no problem.
| -.64 | .55 1.16 .68 |a 12 r20 |
| -.58 | 6.71 1.12 9.44 |b 23 r31 |
| -.40 | -.15 1.15 .78 |c 27 r36 |
I emphasized the infits again. In item b, there's a really big outfit.
My interpretation is that items marked as a, b and c (according to what you explained to me) have off - dimensional data. This could happen for the reasons you said above. So, my conclusion (temptative) is that the test has no multidimensionalty but has three items with off - dimensional data. And the problem of the test is not multidimensionality but three items with off - dimensional data. What i would like to know is if this conclusion is extreme, biased or you have to see more data to get to it. I've read that every data has to be contextualized in the measured sample. So i want to know if my conclusion has to be analyzed further or i can make the statement only based in the results i've shown you and in what you've explained to me.
Thanks for your time and knowledge.
PsychRasch
MikeLinacre:
PsychRasch, Infit and Outfit are usually too insensitive to detect multidimensionality in the data, but we can see that your (A B C) slightly overfit, and your (a b c) slightly overfit.
Most important: is there a substantive (item content) difference between items (r22, r21, r17) and (r20, r31, r36)?
If there is a difference in content, then that difference indicates that the test has a multidimensional aspect. If there is no meaningful difference in content, then the statistical difference between those items may be due to some other feature of the items or the person sample, for instance different item-response formats.
717. Stumped on DIF outcome
Seanswf September 21st, 2009, 9:20pm:
I am perplexed by the following outcome in a DIF report. I am comparing scores on items between 2 time points for the same group.
Person class 1 = Pre-test
Person class 2 = Post-test
I want to see how much easier questions are to endorse on the post-test.
The observed scale I used is 1= hard and 5 = easy.
For the two items below the first one has an observed score which goes from hard (1.50) to easier (3.23) and the DIF measure goes from hard(.59) to easier(.52)... this is logical
But the second item has an observed score which goes from hard (2.66) to easier (3.55) and the DIF measure goes from easy (-1.14) to harder (-.46)??? How can this be?
----------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
| PERSON OBSERVATIONS BASELINE DIF DIF DIF DIF DIF ITEM |
| CLASS COUNT AVERAGE EXPECT MEASURE SCORE MEASURE SIZE S.E. t Prob. Number Name |
|--------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------|
| 1 98 1.50 1.52 .56 -.02 .59 .02 .12 .19 .8485 1 Describe three different modes of client/consultant relationships and the advantages and disadvantages of each |
| 2 92 3.23 3.21 .56 .02 .52 -.04 .17 -.26 .7976 1 Describe three different modes of client/consultant relationships and the advantages and disadvantages of each |
| 1 99 2.66 2.54 -.95 .11 -1.14 -.19 .13 -1.44 .1542 2 Describe PwC's Behaviors and how using these enables one to be a Distinctive Business Advisor and to build long-term relationships|
| 2 92 3.55 3.67 -.95 -.12 -.46 .49 .20 2.46 .0156 2 Describe PwC's Behaviors and how using these enables one to be a Distinctive Business Advisor and to build long-term relationships|
MikeLinacre:
Thank you for this question, Seanswf.
You have two classes (groups) of persons to compare for each item. Please look at Table 30.1 which compares them directly.
You are showing us Table 30.2 which is more useful when there are more than two groups to compare.
Here is the logic in your Table 30.2:
There are two classes of persons (1 and 2) and two items (1 and 2). Each item has a "BASELINE MEASURE". This is the item difficulty from the main analysis in Winsteps Table 14.
From this basline measure, we compute the EXPECTed average score for the class on the item. For person class 1 on item 1, this is 1.52. We compare that with the OBSERVATIONS AVERAGE for the class on the item. this is 1.50. The difference (observed-expected) is the DIF SCORE = 1.50 - 1.52 = -.02.
The class had performed worse than expected by .02 scorepoints. This is equivalent to increasing the item difficulty, DIF SIZE, by .02 logits. So the item difficulty of this item for this class is the DIF MEASURE = BASELINE MEASURE + DIFFSIZE = .56 + .02 = .59 (rounding error).
drmattbarney:
thanks for the clear explanation, Mike, it helped
718. Overflow error in facets
ImogeneR September 21st, 2009, 10:03pm:
Hi Mike,
I just downloaded the new Facets version and I've been experiencing an "overflow error " please see word doc of this above.
I tried using the Hardware= specification and got down to hadware=40 and I also cut out about half the data because I assumed it has something to do with the number of combinations I am asking Facets to run?
I've attached my control and data file of this helps..would you be able to make any suggestions?
Many thanks for all your help! It is an exciting process learning to use Winsteps and Facets - I only wish I had more time to spend on them.
Imogene
MikeLinacre:
Imogene, my apologies for this problem with Facets.
Please email me directly and I will send you a repaired version of Facets. Please attach to your email a zip file containing your Facets specification file and also your Excel spreadsheet containing the data.
Mike ~ winsteps.com
MikeLinacre:
Imogene, thank you for the zip file.
Have emailed you a repaired version of Facets. The repair will be incorporated into the next Facets update.
719. person dimensionality
Raschmad September 21st, 2009, 6:42pm:
Hi Mike,
New versions of Winsteps provide person dimensionality when principal component analysis of residuals is applied to persons. I have problems interpreting this for persons.
1. When "Unexplned variance in 1st contrast" is high or low for persons what can we conclude about the persons or the test?
2. What should we conclude about the persons who form the two opposing clusters on the first dimension? How do negatively loading persons differ from positively loading persons? And what further actions should the test developer take?
BTW, nice pic on Winsteps homepage. Hadnt visited the page for sometime.
Raschmad
MikeLinacre:
Raschmad, please look at any demographic indicators that there are in your person labels. They may indicate in what ways the persons differ. Also Winsteps Table 24.4 indicates which items have the most different profiles for the persons at opposite ends of the contrast.
Action: You may decide you have two different types of persons (e.g., native-language speakers and second-language speakers, boys and girls). Then you must decide how you want to proceed. Here are some options:
1. a compromise measuring-system is good enough (so do nothing more)
2. two different measuring systems are required (analyze two sub-samples of persons separately)
3. one sub-sample of persons is decisive. (Analyze one sub-sample. Anchor the item difficulties. Analyze the other sub-sample).
720. quick question about common person linking
ImogeneR September 16th, 2009, 5:42am:
Hi
I have 3 exams a year sat by a bunch of common persons. I'm trying to work out the best way to equate tests so that I can item bank the set of items for the year.
So, I've inspected scatterplots and there probably are a few more people outside the 95% CI bands than ideal but I'm pusing on anyway.
And, lets just take 2 tests for example.
I want to put test B in the frame of reference of Test A.
I was getting an empirical slope of around 0.86. Is this 'close to 1' or far away from 1 as per the notes in the help section?
I ask becuase when I experiment by doing the 2 different equating procedures I get slightly different results for item difficulties for each version.
For example, when I use PAFILE to anchor the person values of test A into the next run of test B, obviously exactly the same Person measures and then a set of item difficulties.
When I use the method of putting S.D. person test B/S.D. person Test A and then 1/empirical slope as USCALE and x intercept as UMEAN for the second run of Test B I get a slightly different set of person measures, and an empirical slope of 1.067 when I crossplot person measures from this Test B with the original Test A ..and thus the item difficulties are different to the item difficulties in the PAFILE version of Test B rerun.
Would love some advice on what is preferable here? Or is it a matter of perference..or must I have miscalculated somewhere!
many thanks
Imogene
MikeLinacre:
Imogene, we expect different test administrations to produce slightly different item difficulty estimates. So when the item difficulties from one administration are used to measure the persons from a different administration, the person measures will be different from those produced when an administration is analyzed independently.
With two administrations (e.g., pre-test and post-test), there are several questions to ask yourself:
1. Is one administration more important than the other? Is it the "gold standard"?
In education, often the post-test is decisive, because it is used for pass-fail decisions.
In healthcare, often the pre-test is decisive, because it is used for treatment decisions.
If one administration is "high stakes" for the examinees (it will impact them personally) and the other administration is "low stakes", then the "high stakes" administration is decisive.
If one administration is conducted, analyzed and reported before the other administration, it is usually too confusing for your audience if the second administration has different item difficulties. The first administration is decisive.
If one administration is decisive, then its item difficulties are the decisive ones. Anchor the item difficulties of the other administration at the values of the decisive administration.
2. If the administrations are equally decisive:
a) Are the differences (if any) in item difficulty probably due to chance effects, so that next time we expect them to be different, but to roughly the same extent? Then a combined (one-step, concurrent) analysis is indicated.
b) Are the differences in item difficulty systematic, and likely to happen again next time?
Then we are in a Fahrenheit-Celsius situation. We estimate a set of item difficulties which work reasonably well for both analyses (after a linear transformation).
ImogeneR:
Thanks very much Mike.
I have 2 formative assessments in the year and the third is the summative (pass-fail) barrier assessment.
They are all different items (becuase it is the same cohort) but the formative tests are supposed to be indicative of the difficulty of the summative (so the students know what to expect.
The tests don't cover exactly the same content becuase the curriculum is covering more and more topics over the year, but they are all 'basic science' exams.
The summative covers some topics that would be common to the first 2 tests but is weighted a bit more towards content towards the end of the year that have not yet been tested.
In a way they are pre & post tests, (or strictly speaking they are all post tests because learning is supposed to have occurred), and the common person linking showed that student performances across them correlate at about .86.
So from your message and our situation, I would like to consider the last summative as the decisive test.
Because any of the items used in a formative or summative test in the first year could be used in a summative test for the following cohort year, I would like to bank the items at a rasch difficulty level that I would then anchor in the estimation of the following cohorts person estimates.
On the basis of what appears to be a pretty homogeneous cohort (from person linking) I am suggesting I run the the 3 tests together now in a concurrent analysis and use the resulting item difficulty estimates for item banking (where the items show good fit - which they all appear to do..we have only removed 3 or 4 items over the year for poor fit/negative biserial etc).
From the dimensionality map all tests appear to be measuring a single dimension.
Can you see any methodological flaws in this approach?
Many thanks
Imogene
721. person homogeneity
RLS September 18th, 2009, 6:41pm:
I want to investigate person homogeneity with a only two-items scale. Is it possible with LRT or is it plainly nonsense?
Is there a more appropriate method?
Thank you,
RLS
MikeLinacre:
RLS: is this your situation?
You have two dichotomous items, so that the possible raw scores are 0-1-2.
And you want to investigate whether your sample of persons have statistically the same score (i.e., all person variance can be attributed to measurement error)?
RLS:
Sorry for my ambiguity.
The two items are original continuous data, then stratifyed in six categories. I want to investigate if e.g. two samples work on the items because of the same trait. I thought likelihood-ratio test (Andersen) could perhaps provide an opportunity. But for only two items?
MikeLinacre:
RLS, then is this the situation?
You have two 6-category items. They are administered to two samples of persons.
You want to check if the measure distributions of the two samples are statistically the same.
RLS:
Yes and yes, Mike.
If the measure distributions tell me if the two samples work on the items because of the same/different trait, then yes.
Please let me know - if your answer is different - what you think about the usefulness of the likelihood-ratio test to investigate person homogeneity.
MikeLinacre:
RLS, it appears that you want to test whether two samples are drawn from the same population. The statistical challenge is to formulate the null and alternate hypotheses, and then identify a statistical test matching those hypotheses.
A starting point would be to investigate: "Do the two samples have the same mean?" (t-test), then "Do the two samples have the same standard deviation?" (F-test).
722. Using a rasch scale measure for further analysis
lovepenn September 15th, 2009, 11:57pm:
Hi, I'm a novice WINSTEP user and this is actually my first time to apply Rasch Modeling for my study.
I have a basic question for you.
My purpose of study is not just establishing a measure (let's say, self-efficacy variable) from a bunch of items but also analyzing the effect of that variable on children's outcomes.
When I used WINSTEP to do a rasch modeling with 10 items, it produced person data file, which contained "measure", "error", "score" etc. I'm wondering if "measure" variable is something I can directly use for my furtehr analysis (as an independent variable to predict children's outcomes).
Person measure produced in the analysis was in range from -4 to 4 (for example). If I can use this measure for my further analysis, can I change it in further analysis by adding 4 so that the measure ranges from 0 to 8?
Your anwer would be greatly appreciated. Thanks,
MikeLinacre:
Lovepenn, yes and yes.
Rasch "measures" are additive numbers. These are exactly the type of numbers that function best for most statistical techniques.
More sophisticated statistical techniques can also take advantage of the precision ("error") of the measures.
You can linearly rescale the measures and errors for your own convenience:
Your measure or error = (reported measure or error)*a + b
lovepenn:
Thank you for your answer.
Is it also a right way to use rescaling functions in WINSTEPS to obtain a rescaled person measure, such as UIMEAN, UPMEAN, and USCALE?
I saw this in the WINSTEP manual and I just want to make sure if my understanding is right..
And another question, if I need to categorize people based on this linear measure of person ability, can I do this using threshold measure (structure measure)?
Thanks much..
MikeLinacre:
Yes, USCaLSE=, etc., will do a linear transformation of the logit measures for you, Lovepenn.
You can use the threshold measures for stratifying people, but this requires a really clear conceptualization of what you are doing. It is easier to stratify the person sample by comparing them against the item difficulties. This is because the thresholds slide up and down the latent variable, depending on which item they are applied to.
lovepenn:
Thanks again for your answer. I guess I can compare person abilities against the item difficulties using the item-person map, but I'm still not sure technically how to stratify the person sample.
Only thing I can think of right now is doing as follows.
The mean of item difficulties is located at 0 and the SD is 1.
People who are located above 1.0 (1SD above the item difficulty mean) --> Group 1
People who are located between 1.0 and -1.0 --> Group 1
People who are located below -1.0 (1SD below the item difficulty mean) --> Group 3
Something like this???
MikeLinacre:
Yes, that is a criterion-referenced stratification, Lovepenn. It would be even better if there is a substantive change in the meaning of the items, so that each strata corresponds to a definable level of competence on the content of the items below that strata.
723. Measurement at multiple time points
lovepenn September 17th, 2009, 1:49am:
I have some questions regarding measurement at multiple time points.
Suppose that the survey containing the same 15 items asking about stdent engagement was administered to the same sample of students at three different time points, eg, year 1999, 2001, and 2003.
I would like to construct the measure of student engagement using the 15 items and examine if students' engagement has increased or decreased over time.
How can I do this? Can I just separately conduct Rasch analysis of 15 items collected at each time point and then cross-plot item difficulties from different time points to figure out if the measures capture the same phenomenon?
If it is concluded that the measrues capture the same phenomenon, and if one person's ability estimates were 2, 3, 4 at 1999, 2001, and 2003, respectively, then can I just say that this person's ability to endorse engagement items has increased over time?
MikeLinacre:
If you have the three datasets, Lovepenn, it would be easiest to stack them together into one analysis. Code each of the three student's response strings with their years. You can then easily track a student across the 3 years. You can also do a (year x item) DIF study to verify the invariance of the item difficulties.
724. Pivot anchoring
RLS September 4th, 2009, 4:22pm:
I have a scale where it was necessary to collapse categories, but in a different way, e.g. 0000123, 0001123.
PCM was applied. Now I want the primary item difficulty to compare the items. I know pivot anchoring.
My question is now, where can I see which amount I have to add/subtract for each item in the SFILE? Is there a practical application? (because there are many items)
Many Thanks!
RLS
MikeLinacre:
This is difficult to manage, RLS.
Look at Winsteps Table 2.2.
Pivot anchoring does not change the horizontal appearance of each line, but it does change the vertical ordering.
Use your text-editor to re-order the items vertically into the order that makes sense.
Look at the category numbers. Is there a category number which ascends upward and rightwards through the reordered item lines? If so, this is the category number for the SAFILE=
If there is not, then you will need different SAFILE= values for different items. Winsteps Help may assist you with this.
RLS:
Thank you very much for your reply.
Unfortunately it is not really possible to re-order the items because of their meanings.
I tried some things with anchoring, but without success. I do not know which amount I have to change the values in the SAFILE.
Perhaps it is easier and more effective to make a run without collapsing, even if the parameters are not so stable?
I have forgotten to say that there are also items with original different categories. But each item has centered categories,
e.g. -- - ~ + ++, -- - + ++.
I am especially interested in the item map (Table 12.2). Thank you again.
RLS
MikeLinacre:
RLS, yes, there is a problem when item categories are collapsed in different ways across the items. The rating-scale has different meanings for different items. This makes it difficult to compare items, and to communicate your findings to your clients. Since the meaning of the "primary difficulty" is different for different items, you may not be able to compare them in a way that makes sense to your audience.
725. Local independence and model fit
ong September 4th, 2009, 7:52pm:
Dear Mike,
I have 48 dichtomous items where partial credit are awarded for partial responses and items that share common stimulus.
Checking on the standardised residual correlation, for items where partial credit are awarded for partial responses, the correlations are rather high for pairs of items(>0.4). For the items that share common stimulus, some indicating high correlation, some indicating low correlation.
To account for this violation of local independence, I summed the dichotomous items and modelled them as polytomous items.
How can I show that PCM is a better fit model than the dichotomous model?
Do we consider PCM and dichotomous model nested models?
Does Winsteps provide deviance output? If yes in which Table?
Thereotically, items sharing common stimulus have been cited as the causes of violation of local independence. However, for my data the results based on the standardised residual correlation has not been consistent.
Would a thereotical argument or the empirial evidence facilate the decision to model items as dichotomous or polytomous for items sharing common stimulus?
Thanks
Ong
MikeLinacre:
Thank you for these questions, Ong.
First we need to ask ourselves; "What is the influence of local dependence on the person measures?"
Suppose we put the same item into our test twice. There would be very high local dependence between the two items. The effect would be to increase the spread of the person measures. In Classical Test Theory, this is called "the attenuation paradox" = an increase in reported test reliability without an increase in the underlying statistical information.
So, the effect of collapsing locally-dependent items into polytomies is to reduce the spread of the person measures. If the items are highly locally-dependent, then you may also want to collapse together categories of the polytomous items.
Global fit: since the number of estimated parameters has not changed when you transform from dichotomies to polytomies, all you need to do is to compare the sum of the squared standardized residuals.
Nesting: we can always go from dichotomies to polytomies, but not, in general, from polytomies to dichotomies. So the nesting is only one way.
"Polytomous or dichotomous" - usually the statistical evidence is not strong in this decision. More important are i) the meaning of the items and ii) communicating our findings to our audience. If the audience are interested in individual items, or the audience would be confused about a polytomous analysis, then report a dichotomous analysis. Since the raw scores are the same, the ordering of the persons will not change. There will only be a small change in the spread of the sample.
Suggestion: cross-plot the person measures for the dichotomous and polytomous analyses. Is the difference big enough to have practical consequences?
726. Table 1.4 in WINSTEPS
wlsherica August 12th, 2009, 12:34pm:
Dear Mike,
I had a question about the Table 1.4(Polytomous distribution map) in WINSTEPS.
(https://www.winsteps.com/winman/index.htm?dif.htm)
According the manual, this table shows the distribution of the persons and items. However, what's the difference between Table 1.1(Distribution map) and Table 1.4?
What kind of information could I learn from this table?
Thank you!
wlsherica
MikeLinacre:
Do you have items with more than two categories (polytomous items), Wisherica?
Table 1.4 is usually only produced for polytomous items. If you do, then Table 1.4 is useful for indicating the operational range of your rating scale or partial credit items. It is typical for the operational range of polytomous items to be wider than the sample. For a more detailed picture of the same information see Table 2.3. this identifies the items.
Table 1.1 shows the person distribution and center column of item difficulties from Table 1.4, so it does not show the operational ranges of the the polytomous item.
wlsherica:
Thank you for your reply.
Yes, I have items with five categories. I'll see Table 2.3 for more details and I
think I got the point. =]
727. Missing in the data matrix (RUMM) ...
Andreich July 28th, 2009, 9:00am:
Hello. I have a question: How the RUMM2020 calculates items difficulty and person ability if matrix contain missing data? May be this software changes "_" in to "0"?
MikeLinacre:
Usually, missing data is treated as "not administered" in Rasch analysis, Andreich. This makes Rasch ideal for analyzing data collected using computer-adaptive tests. Persons are measured based on the items to which they responded. Items are measured based on the persons who responded to them.
RS:
Hi Andreich
As Mike mentioned, RUMM, like other Rasch softwares, treats missing data as "not administered". But remember to recode missing as "zero" for measurement purpose. Otherwise you would get different measures for the same raw score as RUMM uses Pairwise Maximum Likelihood Estimation (PMLE) method.
RS
RS:
One more point. If missing data is "not administered" like when combining data from two test forms with common items for simultaneous calibration you would need to get two conversion tables, one for each form. This can be done by using the "equating tests" option in RUMM.
RS
728. LOOKING FOR A STUDY
mathoman August 5th, 2009, 2:27pm:
HI ALL,
I AM LOOKING FOR STUDIES (SEARCH PAPER) DEAL WITH STANDARDIZE A TEST (IN MATH) OR CONSTRUCT IT USING RASCH MODEL? I WANT GETTING USEFULL OF THE MOTHEDOLOGY.
COULD ANY ONE HAVE SOME OF THEM, PLEASE?
I NEED YOUR HELP ALL SOON...
MikeLinacre:
Here are some Rasch papers that are available on the Internet. Perhaps one of them will help you, Mathoman.
www.ajpe.org/legacy/pdfs/aj660304.pdf
Validation of Authentic Performance Assessment: A
Process Suited for Rasch Modeling
www.uky.edu/~kdbrad2/Rasch_Symposium.pdf
Constructing and Evaluating Measures: Applications of the Rasch Measurement Model
www.cemcentre.org/Documents/CEM%20Extra/SpecialInterests/Rasch/Psycho%20oncology%20preprint.pdf Rasch Analysis Of The Dimensional Structure Of
The Hospital Anxiety And Depression Scale
www.jalt.org/pansig/2005/HTML/Weaver.htm
How entrance examination scores can inform more
than just admission decisions (Skip over the Japanese)
mathoman:
THANK U DR. MikeLinacre
729. David Andrich Rating Scale
knaussde August 6th, 2009, 1:12am:
How do I perform the David Andrich Rating Scale analysis in SPSS?
MikeLinacre:
This is challenging, Knaussde.
One approach is to express the Andrich logit-linear model as a log-linear model, and then use the Generalized Linear Models component of SPSS.
http://epub.wu-wien.ac.at/dyn/virlib/wp/eng/mediate/epub-wu-01_d64.pdf?ID=epub-wu-01_d64 PDF pages 123-128 show the instructions for GLIM. There are probably equivalent ones for SPSS.
730. table convert
danielcui July 23rd, 2009, 8:24am:
hi mike,
how to export winsteps table to word file without rag? thank you.
daniel
MikeLinacre:
Daniel,
Copy-and-paste the Table into Word
Then format the table with Courier New or Lucida Sans Console
Alternatively, copy the Table (or the equivalent output file) into Excel. ("Data", "Text to columns" - if necessary). Then you can use Excel to format the Table how you would like.
A nice feature in Excel is to "hide the cell borders" (Select the cells, Formatting, Borders).
danielcui:
hi mike,
thanks for the comments. but it still seems not optimistic. see attached file.
danielcui:
also, how do I change the logit scale to fit a 0 to 100 with certain winteps Uscale. see the sample enclosed. thank you.
MikeLinacre:
Daniel:
In your Word document, replace all spaces with non-breaking spaces ^s
USCALE:
1. Do your ordinary analysis.
Look at the logit range , -3 to +4
Decide what range you want: 30 to 100.
Go to the Winsteps Help menu. Bottom entry: "Scaling calculator".
Click on it. Enter your values.
click on "compute new"
click on "specify new"
Redisplay your Table from the Tables menu
The job is done!
danielcui:
thanks you mike for the USCALE. I've accomplished the conversion.
but I don't quite understand the word document change, could you describe in more details?
MikeLinacre:
Certainly Daniel,
Paste you table into Word
Ctrl+H (replace)
Find what? press on your space-bar (one blank space)
Replace with? ^s (non-breaking space)
Find - should find the first space
Replace - should look apparently the same
Replace All - should correctly format your Table.
OK?
danielcui:
Thanks a lot, Mike, It fixed.
danielcui:
one more question on the table/map,Mike, how export the item-person map,or other table in a figure/picture format? since I need attach the result as a manuscript figure. Thank you.
MikeLinacre:
One possibility is to use Excel, Daniel.
www.winsteps.com/winman/excelitemmap.htm
danielcui:
thank you so much, mike. I made it.
MikeLinacre:
Great!
Those maps are challenging, Daniel!
Mike L.
731. min diff between category thresholds
waldorf_jp July 27th, 2009, 10:28am:
Dear Dr. Linacre,
First time on the forum, but I'm finding lots of helpful comments--thank you. My question: I'm working with several 7-point Likert scales using Winsteps, and while checking category function I'm wondering about the minimum acceptable separation between adjacent categories. In Wolfe & Smith (2007), I find values for 3-pt, 4-pt, and 5-pt scales (1.4, 1.1, and .81 logits, respectively), but can't find any further guidelines in RMT or elsewhere.
Thanks in advance!
MikeLinacre:
Waldorf, there are general guidelines for rating scales under Rasch conditions at www.rasch.org/rn2.htm
732. Differences between two measures
Hidetoshi_Saito July 17th, 2009, 8:18am:
Hello,
I've learned that when testing differences between two measures, we could use:
t = (M1 -M2) / squareroot(SE1� + SE2�) and t> 3.0 when significant.
But how can we calculate the denominator degrees of freedom and p-values.
Is there any SPSS macros to do this job?
Thanks in advance.
Saitofromjapan
MikeLinacre:
Saito, the d.f. depend on the number of observations.
Use the Welch-Satterthwaite formula:
d.f = (SE12 + SE22)2 / (SE14 / (N1-1) + SE24 / (N2-1))
where N1 and N2 are the counts of observations in M1 and M2.
Then look up the p-value using Student's t-statistic.
There is a probably a calculator on a statistics website which does this ...
Hidetoshi_Saito:
Thanks Dr. Linacre
I found this here
https://www.winsteps.com/winman/index.htm?t_statistics.htm
Why is the one in here is a bit different from the one you gave me?
Many thanks.
saitofromjapan
MikeLinacre:
Thank you for checking up on me, Saito. Sorry, there was a typographical error in my post. Now corrected. They should now be the same.
733. 1-parameter versus 2-parameter Question
rblack July 15th, 2009, 8:20pm:
Hi,
I have a question regarding the comparison of a rasch partial credit model (in Winsteps) and generalized partial credit model (in PARSCALE). Note that some items are dichotomous and some are 3-point ordered categories.
I've read in multiple sources that one way to assess if the 2-parameter model is fitting better/worse at the item level is to plot the expected ICC and the empirical (data driven) ICC for each item. The closer the curves, the better the fit. This can be easily done in Winsteps, but unfortunately, the closest thing I could get in PARSCALE was through a type of add-on program, called ResidPlots-2. This program gives, I think, the expected ICC and residuals.
http://www.umass.edu/remp/software/residplots/ResidPlots-2Manual.pdf
Any suggestions on how to compare the item level ICCs from each model given the information I provided? Should I try to obtain the residuals in Winsteps?
Any advice would be greatly appreciated!
Thanks
MikeLinacre:
This one is a tough one, Ryan.
Usually fit of nested models is compared using chi-square statistics.
I'm not sure how well a visual comparison would work. In most cases the PCM and GPCM ICCs are similar. Fit is difficult to assess by eye because the plotted points are themselves averages. The fuzziness due to misfit is largely hidden.
You can see how this works in Winsteps by moving the "empirical" slider left and right under the empirical ICC graph. The smaller the interval, the noisier the ICC line.
rblack:
Hi Mike,
Thank you for responding. So, your recommendation would be to compare these models only by the overall fit (i.e. Chi-Square test on difference of the -2*LLs)? There's no clear way to do item-by-item comparisons across models? Also, if you have the time, out of curiousity, are the empirical ICCs the same as the residuals?
Thanks again for all your help.
Ryan
MikeLinacre:
"item by item" - Ryan?
This depends on what options are available in PARSCALE. If PARSCALE allows you to pre-set discriminations, then the Rasch PCM model in PARSCALE is to have all discriminations the same. You could then relax that constraint for each item in turn.
Statistically, the global log-likelihood chi-square is typically used for this type of comparison.
If the choice of model is made on purely statistical grounds, it is likely to fall foul of accidents in the data. There should be strong substantive, as well as statistical, reasons for your choice of model. If you can predict in advance which items and categories will be more discriminating, and the GPCM confirms your prediction, then you may be on firm ground with GPCM. But if you are hoping that GPCM will solve the inferential problems, then the next dataset will lead to different inferences.
Residual = observed - expected. There is one residual for each observation. There is a model ICC (plotting the expected values of the observations) and an empirical ICC (plotting the observed values of the observations) for each item.
rblack:
Hi Mike,
You always give great practical advice! I hadn't thought of running the model in PARSCALE and permitting the slope of one item at a time to be estimated freely. I like this idea. What I've found challenging is the dramatic difference in -2*LLs between the Rasch model run in Winsteps and the Rasch model run in PARSCALE (forcing equal slopes). I'm referring to literally tens of thousands of -2LL points difference between both rasch models, which ends up changing the end result (Rasch versus 2-parameter). I've received help on constructing both models in both programs, so I think they are technically correct. Anyway, I digress. This is something I'll try to work out and if I find any useful tips for folks I'll repost. I can't be the first person to encounter this issue.
Also, your point about the substantive component is important, and something I have thought about.
The residual explanation makes complete sense (similar to general linear models). Thanks for clarifying.
Thanks again,
Ryan
MikeLinacre:
Ryan, "thousands of -2LL points difference"
Yes, that is due to the many unstated (but necessary) statistical assumptions built into the software packages in order for them to work. So it is difficult to compare chi-squares across software packages. For instance, PARSCALE specifies that some parameters are normally distributed and other parameters are log-normally distributed. Winsteps does not have those statistical constraints, but Winsteps has other ones.
734. discrimination parameter estiamte under Rasch
herethere July 13th, 2009, 1:14pm:
How can I find the value for the discrimination parameter in WINSTEPS under the Rasch model? WINSTEPS does give discrimination parameter estimates as if a 2PL model had been used. But what is the discrimination parameter estimate for a Rasch model? The Rasch model says that the discrimination parameter is a constant across items, but still it has some value, isn't it?
Thanks!
MikeLinacre:
The constant discrimination value in Rasch is usually set to 1 so that the estimates (measures) are reported in logits, Herethere.<br>
USCALE = 1 (the default value).
When the estimates are repored in (approximate) probits the discrimination is set to 1/1.7 = 0.59. The Winsteps instruction for probits is:
USCALE = 0.59
herethere:
Thanks for your answer, Mike. So if I I specify the person mean to be 0 and person SD to be 1, that is, if I specify UPMEAN=0 and USCALE = 1 / (person S.D. in logits), then the constant discrimination value in Rasch is 1 / (person S.D. in logits). Is it correct?
Thanks again!
MikeLinacre:
This is the computation, Herethere. It is counter-intuitive.
USCALE = 1 / (person S.D. in logits) converts from logits into "person S.D. units".
The Rasch model (written in logit-linear form) is
log (P/ (1-P)) = a (B'-D')
where B' = ability in Person S.D. units
D' = difficulty in Person S.D. units
and the "discrimination" = a = 1 / USCALE = conversion from person S.D. units back into logits = person S.D. in logits.
735. Checking my test equating interpretations..
ImogeneR July 13th, 2009, 5:14am:
Hello All,
I've been practising using MFORMS to get concurrent analysis of some med student tests across years (with some small number of common items).
I think I have the technique down, but just wanted to clarify if some of my interpretations and expectations about what I can now DO with my concurrent analysis in terms of comparing difficulties of test administrations and for item banking are in anyway on track.
So, what I have done is looked at the common items, and discovered that this sit quite nicely in the confidence intervals so decided that concurrent equating is appropriate.
My data is like this:
Test A:
80 items
249 people
Test B
97 items
260 people
There were 7 common items.
After running the concurrent analysis I partitioned out the separate years to look at item /test measures. (Using ISELECT common+individual test items ) and PSELECT for the year.
Then I looked at the mean measures of items within each 'test' from the concurrent analysis and found Test B on these grounds had a mean item measure of about 0.4 logits overall than Test A. Is this a valid interpretation from the means of item measures grouped by administration within a concurrent analysis?
Then I looked at the score tables for each Test administration within the concurrent and concluded that to have an equal passing 'standard' I should pick a MEASURE and then use the different but corresponding raw score from each table as the cut score..correct?
I did a t-test of the item measure groups mean difference and this was close to , but not significant (difference in the difficulty of the tests going by concurrent analysis)- is this also a valid interpretation? (Although the actual significance would come down to how many raw points in the confidence intervals here I guess in terms of impact on where the cut score might go...?)
ITEM BANKING
So now that I have done my concurrent analysis ..is it safe to at least 'bank' my common items at their Rasch difficulty levels from the concurrent analysis - can I also 'bank' the others at their concurrent analysis difficulties?
What happens if I want to equate with a third test?
Although these questions might seem silly, I quite excited about being able to really PRACTICALLY using Rasch in my work! These are high stakes exams and I need to be able confidently pinpoint each administration test difficulty to keep our standard consistent. Anyones experience here would be gratefully received! (Any useful readings on the topic would be much appreciated also ;D )
Kind regards,
Imogene
MikeLinacre:
All your statements sound correct to me, Imogene.
Except that I don't understand: "I did a t-test of the item measure groups mean difference"
What are the "item measure groups"?
ImogeneR:
Thanks for your response Mike, and sorry, what I meant was the t-test of means of the 2 different sets of items (a set for each year) in the concurrent analysis. It was "approaching significance" in statistical terms, and I am proposing that the confidence intervals in the t-test (upper and lower bounds) could be used like an SEM in establishing a borderzone score range (and thus take the top or the bottom of the CI as the cut score depending on purpose of assessment.
Thanks again.
MikeLinacre:
Thank you for the explanation, Imogene. Your idea is new to me. It will be instructive to know how well it works .... :-)
736. Minimum sample size for item step estimation
mdeitchl July 9th, 2009, 7:53pm:
Hi -
I am analyzing polytomous scale data (3 frequencies; 2 item steps). I have read that each category for an item should have at least 10 observations responding positively; 10 observations responding negative; for stable item calibration. If this minimum of appx 10 observations positive/negative responses for each category is not met, I am unclear if this would: 1. affect only the item step calibration with few observations; or 2. the calibration for all steps of that item; or 3. make the calibration of all item steps for all items in the scale unstable.
Thanks in advance.
Megan
MikeLinacre:
The step calibrations of all the steps (Andrich thresholds) are estimated as a set together, Megan, so if one is unstable, they all are, and, since the item difficulty is usually set at the average of the thresholds, the item difficulty is also unstable.
This is one reason against the partial credit model, and in favor of grouping items to share the same rating scale whenever meaningful. Then the items strengthen each other, because there are more observations in each category.
737. Winsteps Item Fit Table Export Options
rblack July 2nd, 2009, 5:35pm:
Hi,
I'm trying to copy and paste the values going down each column of the item misfit table, and this is not possible in notepad.
Concretely, this is what I see:
ENTRY TOTAL ... INFIT ...
NUMBER SCORE ... MNSQ ZSTD ...
X X A X
X X B X
X X C X
. . . .
. . . .
. . . .
Is there a way to select the column with values A, B, C... while not highlighting the entire "rows" of A, B, and C... I want to be able to copy the entire MNSQ column [without any other columns].
Thanks,
Ryan
MikeLinacre:
Thank you for your question, Ryan.
How about using the Winsteps "Output Files" menu, and outputting the IFILE= (items) or PFILE= (persons) to Excel?
Alternatively, you can use a word processor or text editor with a "rectangular copy" feature. In Word, this is "alt+Mouse", also in TextPad and the freeware "NotePad++".
connert:
Excel is not a good program to do statistical analysis from. There are many questions about their statistical routines. Even though I am not a fan of SPSS you are more likely to get credible results if you save the person or item data in a SPSS sav file. Or any of the other available options except excel.
MikeLinacre:
Fine, Connert. The numbers are the same in every format, so the choice is the analyst's.
rblack:
Perfect! Thank you, Mike!
738. Bonferroni adjustment and DIF
ong July 2nd, 2009, 9:14am:
Dear Mike,
I read this article on DIF comparing Science and non-Science majors in a placement test by Weaver (2007)
http://jalt.org/pansig/2007/HTML/Weaver.htm
When alpha is set at 0.05, Weaver computed the Bonferroni adjustment = 0.05/2. referring to the number of groups and not the number of items.
I am working on gender DIF with 50 items.
Some suggest that to compute bonferroni adjustment = alpha/number of items to adjust for the multiple t-test comparison to adjust for 1 out of 20 chance that the hypotesis is rejected by chance when alpha is set as 0.05.
So, following this Bonferroni adjustment = 0.05/50 = 0.001. Taking this value, fewer items flagged as DIF.
But if the Bonferroni adjustment = 0.05/2 as in Weaver article, there ia high percentage of items flagged as DIF.
Why do you think there is this two different view points on the computation of Bonferroni adjustment?
When should one use Bonferroni adjustment?
Does Bonferroni adjustment help in interpreting the result?
Thank you
Ong
MikeLinacre:
Thank you for your questions, Ong.
Before making any adjustment to a probability level or a t-statistic, we need to define the hypothesis we are testing exactly. Then the hypothesis will tell us what adjustment to make. For instance:
Null Hypothesis 1. "There is no DIF for item 1." - No Bonferroni adjustment: if p < 0.05 for item 1, then reject the null hypothesis of no DIF for item 1.
Null Hypothesis 2. "There is no DIF on items 1 and 2." - Bonferroni adjustment: if p < 0.05/2 for either item 1 or item 2 or both, then reject the null hypothesis of no DIF for items 1 and 2.
Null Hypothesis 3. "There is no DIF on any of the 50 items on the test." - Bonferroni adjustment: if p < 0.05/50 for any of the 50 items of the test, then reject the null hypothesis of no DIF on any of the 50 items.
In Hypothesis 2 or 3, we do not flag individual items, we flag the set of items. If you want to flag individual items, then you are using Hypothesis 1.
You could do this in 2 stages. (i) Is there any DIF on the test (Hypothesis 3 for all items) ? (ii) If so, which items have DIF (Hypothesis 1 for each item) ?
Lawyers are not interested in Hypothesis 2 or 3, they are only interested in Hypothesis 1. They look at the items and say: "It looks like item 23 is biased against my client. Show me the statistics for that item". Lawyers are not interested in global fit tests for DIF, like Hypotheses 2 and 3.
739. Item misfit
wlsherica June 29th, 2009, 9:32am:
Dear Mike,
I have some questions about item misfit. I had a questionnarie with 15 items, and I found there were 7 items misfit. Is it correct to delete all of them if I'd like do further analyses ? Could I keep them if I think some of them have important meaning?
Becuase I have to make sure the further analyses will be reasonable.
Thank you for your help.
MikeLinacre:
Thank you for your questions, Wisherica.
What criteria are you using to decide that an item misfits? It is unusual for a reasonable item to misfit so badly (mean-square > 2.0) that it damages measurement.
wlsherica:
Thank you for your reply. Yeah, I was shocked about the result .....
The criteria I used are as follow,
1. 0.6 <MNSQ < 1.4
2. -2 < ZSTD < 2
The questionnaire is about quality of life in diabetic patients.
If one item didn't fit these two criteria simultaneously, I define the item is misfit.
What's wrong with these items?
MikeLinacre:
Thank you for your numbers, Wisherica.
0.6 <MNSQ < 1.4 - this reports how big the misfit is
-2 < ZSTD < 2 - this reports how unexpected the misfit is, when the data fit the Rasch model.
Advice: Always drop out underfitting (high mean-square) items and then reanalyze before dropping out overfitting (low mean-square) items. This is because average mean-squares are forced to be near 1.0. So large mean-squares force there to be low mean-squares.
Overfit (the lower numbers) usually has no impact on the quality of the measures. It merely indicates that the items are less efficient. So, if this is a pilot test, we would drop these items or replace them with more efficient items.
ZSTD<2 - this depends on your sample size. The larger the sample size, the more statistical power for detecting misfit.
So, the crucial question is: "Do you require perfect perfect items, or are useful items good enough?"
If in doubt,
1. Drop out conspicuously malfunctioning items.
2. Analyze the data and save the person measures
3. Drop out all the doubtful items
4. Analyze the data and save the person measures.
5. Cross-plot the two sets of person measures (steps 2 and 4): what has changed? If nothing important has changed (or the step 4 person measures are worse than step 2 person measures), then the step 2 analysis is better than the step 4 analysis. Keep the doubtful items.
wlsherica:
Thank you so much for your advice, Mike.
One more question, does I have to use excel or other software for drawing
cross-plot ?
(I used WINSTEPS for Rasch analysis.)
Thanks again =]
MikeLinacre:
Sorry, Winsteps does not have graphing capabilities, Wisherica. Winsteps can call Excel from the "Plots" menu if Excel is installed on your computer.
If you do not have Excel or another plotting program, then there are freeware programs, http://statmaster.findmysoft.com/ is a possibility
wlsherica:
Oh, great, I have Excel on my computer.
Is the "Plots" menu or "Output files" menu ??
Thank you for your help so far.
MikeLinacre:
Wisherica, the scatterplot (XYplot) is on the Winsteps "Plots" menu: www.winsteps.com/winman/index.htm?comparestatistics.htm
wlsherica:
Thank you so much, Mike !
I got the point ! =]
740. centering set up in FACET for partial credit model
brightle March 5th, 2009, 9:42pm:
Hi all,
I am using FACET to check ability estimates of examinees using a 3-facet MFRM (person, rater and item respectively).
I didn't specify the center= or noncenter= command in the beginning. The FACET software seemed centered the item facet by default.
Later I realized that I need to center the item facet, and added one line in the SPE file (CENTER=3).
The two calibrations results were quite similar, except the person ability estimates differed by about 1 point. I would appreciate if someone or Mike could help to explain it. Which specification is the right one?
Thanks.
Brightle
the code:
; FACFORM
; from keyword file: crossed.key
Facets=3 ; three facets, person, rater, and Item
Title = Crossed Design data1.dat
Output = data1.out
score file = data1.sco
CSV=yes
Pt-biserial=yes
center=3 ; shall I add this line for the calibration?
Convergence = 0, .0001
Models = ?, ?, #,R5
Data file = data1.fac
labels=
1, person; the person facet
1
2
3
4
5
6
7
8
9
10
*
2, rater; the rater facet
A
B
C
*
3, item; the item facet
1=item1
2=item1
MikeLinacre:
The choice is yours, Brightle. The analysis needs every facet except one to be centered. This is to define the "local origin", the zero-point of the measurement scale.
The default is that Facet 1 is non-centered. This is "person" in your data. Facets 2 and 3 are centered, "rater" and "item". This would be my choice.
If this was a study of rater behavior, you might prefer to non-center the raters:
Noncenter = 2
Then the persons and items would be centered, and the raters non-centered.
If you are not sure what you want, it is usually safe to let Facets use its default values.
brightle:
Hi Mike,
thanks for your quick reply. it makes sense to me. I followed your suggestion on the centering constraints.
However, I have a related question on the scaling issue when I am trying to compare the simulated results. I would appreciate greatly if you could help me to figure it out.
Suppose I am doing a simulation study.
500 examinees normally distributed ~ N(0,1);
with 2 items, location parameter is -.496 and .05 respectively;
4 step parameters for each item that summed up to zero (rated scores can be 0-4);
and 2 raters (fully crossed design), with the leniency parameter of -.5 and .3 (Negative means more rigorous and positive means more lenient).
If I generated the data without forcing the item location parameter and raters' parameter to be summed up as zero, but constrained them as zero in the calibration (as we have discussed in the previous two emails). Do you think I need to rescale the estimated parameters in order to compare the estimated item parameters and person ability to the true parameters? If yes, do you have any recommendation on how to do this?
Thanks.
Brightle
MikeLinacre:
Thank you for your questions, Brightle.
It looks like you need to use "group-anchoring" in your Facets analysis in order to make the Facets estimates directly comparable with the simulations.
Either:
Center the examinees
Group-anchor the raters:
Labels=
...
*
2, Raters, G
1, rater 1, -.5
2, rater 2, .3
*
Noncenter the items
Or:
Center the examinees
Non-center the raters:
Group-anchor the items:
Labels=
...
*
3, Items, G
1, item 1, -.496
2, item 2, .05
*
OK?
brightle:
Hi Mike,
thanks for your help. since my simulation is done already, it is pretty complicate for re-setting up all the parameters.
there is one thing I forgot to mention in the last post, that the two items are always the same, while the examinees are a random sample from a larger population.
in this sense, it is actually item-anchor instead of person anchor (group anchor).
Is there any way that I can rescale the ability estimates in the original scale by rescale the item location parameters?
For example, is it ok if I just minus the ability estimates by the mean of the two true location parameters.
that is
theta_hat_rescaled=theta_hat - ((-.496+.05)/2)
theta_had is the estimated ability, and theta_hat_rescaled is the rescaled estimates of theta based on the true item location parameter.
please let me know what you think about it.
Thanks
Brightle
MikeLinacre:
Certainly, Brightie. You can change the local origin (zero-point) to suit yourself. But be sure to maintain the relative relationships of everything.For instance, if you add "1" to all the person abilities, you also add "1" to all the item difficulties or add "1" to all the rater severities.
741. Some Rasch/Winsteps questions
RLS June 17th, 2009, 5:13pm:
1) I sometimes read (e.g. in Winsteps help) that item-total-correlation should be positive, but the size of a positive correlation is of less importance than the fit of the responses to the Rasch model. In some scales I have really low correlations (e.g. 0.1 or 0.2). Has this really no negative influence to the measures, especially if the test has only few items (e.g. 5)?
2) I often read that if likelihood ratio tests are not significant, than the rasch model is valid, which means the test is "homogeneous". I have a test with 5 items where the item-total-correlations are only between 0.0 and 0.2 and the LR tests are not significant. How is this possible?
3) I want to model items together which could share the same rating-scale structure. Is it sufficient only to look at the category probability curves or multiple ICCs without regarding the values of "obsvd avrge" and "structure calibratn"?
4) Are there attempts applying the rasch model to data which is primarily continuous and is classified in order to use?
5) A conventional factor analysis with items of a test battery suggests two factors. In two PCMs I modelled the corresponding variables together and did PCAs of Rasch residuals with following results:
-- Empirical -- Modeled
Total raw variance in observations = 74.7 100.0% 100.0%
Raw variance explained by measures = 20.7 27.7% 27.2%
Raw variance explained by persons = 6.3 8.4% 8.3%
Raw Variance explained by items = 14.4 19.3% 18.9%
Raw unexplained variance (total) = 54.0 72.3% 100.0% 72.8%
Unexplned variance in 1st contrast = 4.3 5.8% 8.0%
Unexplned variance in 2nd contrast = 3.5 4.7% 6.5%
Unexplned variance in 3rd contrast = 2.9 3.9% 5.4%
Unexplned variance in 4th contrast = 2.5 3.4% 4.7%
Unexplned variance in 5th contrast = 2.4 3.2% 4.5%
Total raw variance in observations = 72.2 100.0% 100.0%
Raw variance explained by measures = 17.2 23.8% 24.7%
Raw variance explained by persons = 5.1 7.1% 7.3%
Raw Variance explained by items = 12.1 16.8% 17.4%
Raw unexplained variance (total) = 55.0 76.2% 100.0% 75.3%
Unexplned variance in 1st contrast = 5.0 7.0% 9.2%
Unexplned variance in 2nd contrast = 3.0 4.1% 5.4%
Unexplned variance in 3rd contrast = 2.8 3.8% 5.0%
Unexplned variance in 4th contrast = 2.6 3.6% 4.7%
Unexplned variance in 5th contrast = 2.5 3.4% 4.5%
I regard that in 1st contrast only 4.3 of 54.0 items are unexplained variance (RPCA1). Certainly 4.3/20.7 does not look so fine ...
Is the construction of two global indeces according the RPCA indicated?
Many Thanks!
RLS
MikeLinacre:
Thank you for your questions, RLS. Here are some thoughts ...
1. Correlations. Does your copy of Winsteps also reports the expected value of the correlation? If so, this gives you an indication of whether a correlation of 0.1 or 0.2 is reasonable or not. www.rasch.org/rmt/rmt54a.htm shows the maximum value of the correlation for items of different targeting on the sample.
2. "if likelihood ratio tests are not significant, than the Rasch model is valid,"
Statistical significance tests can only report probabilities. So "not significant" means "when the data fit the Rasch model, the probability of observing data with misfit like these or worse is greater than p=.05". This is far from saying "the Rasch model is valid for these data". It only says, "this LRT test does not provide strong evidence that the data do not accord with the Rasch model." A different fit test could provide that evidence. In your situation, the LRT fit test probably does not have enough statistical power to report significance.
3. Usually we want to model items together whenever that is meaningful. So please do that, then check the category-level fit statistics (e.g. Winsteps Table 14.3) to verify that the categories fit with the grouped items.
4. There are several approaches to continuous data. www.winsteps.com/winman/decimal.htm suggests some.
5. The unexplained variance in your first contrasts are 4.3 and 5.7. These correspond to a strength of 4 items and 5 items. We do not expect to see values above 2.0 by chance https://www.rasch.org/rmt/rmt191h.htm. So, it is likely that there is secondary dimension in your data which is generating this contrast. Look at the substantive difference between items at the top and bottom of the plot in Table 23.2 to identify the meaning of the secondary dimension. If this difference in meaning is important to you, then two separate Rasch analyses are indicated:
Example: an arithmetic test. The contrast-difference is between "addition" and "subtraction" items. Is this difference important? To the State Director of Education, no. To the "Learning Problems" guidance counselor, yes.
RLS:
Thank you for your reply! It is very helpful.
1. Are there experienced data / guidelines if the difference between exp. and obs. correlation is reasonable?
E.g. I have .00/.04/.13/.24 (obs) and .31/.15/.33/.30 (exp).
4. Do you know, if there are attempts applying the rasch model to physiological data?
5. If I say, the first contrast corresponds to a strength of 4 items, which is compared to 54 items not really much and if I say I only want "global" indeces, it could be an approach, right?
Yet another question: "if mean-squares are acceptable, then Zstd can be ignored" (Manual, p. 444)
E.g. my fit range is 0.5-1.5 and one item has MNSQ 1.4 and ZSTD 3.3, so I can ignore the large ZSTD value?
MikeLinacre:
Thank you for your questions, RLS.
!. "the difference between exp. and obs. correlation is reasonable?"
Reply: I don't know. Can anyone else answer this?
4. Physiological data?
Reply: Please Google - Physiological Rasch - some webpages look relevant.
5. "4 items, which is compared to 54 items"
Reply: The meaning of the items is important. 4 tennis-skill items would be invalid on a language test of 100 items.
"one item has MNSQ 1.4 and ZSTD 3.3, so I can ignore the large ZSTD value?"
Reply: This depends on what your purpose is.
ZSTD 3.3 says "this item definitely does not fit the Rasch model perfectly"
MNSQ 1.4 says "this item fits the Rasch model usefully enough for most practical purposes"
So, if you are testing a new item for inclusion in a test, this item may not be good enough,
but, if you are using the item to measure people, then the evidence against the item is probably not strong enough to disqualify the item.
RLS:
Thank you very much again. I really appreciate your help.
1) Now I think, the coefficient of determination (RSQ) helps a little bit to decide if the difference between exp. and obs. correlation is reasonable or not.
I have two groups in association with small obs. RSQs: very small exp. RSQs (e.g. 0.14) and exp. RSQs which maybe play a not insignificant role (e.g. 0.30).
Sorry for asking a question again but it is quite important for me.
I have a scale with unfitting categories. In some items the lowest 3 (of 6) categories are not at all selected. So I collapsed the categories to have a minimum of 10 observations in one category. One the other hand I have few items where collapsing is not really necessary. Grouping items together is hardly possible, because the structure of the scales are quite different, so I apply PCM.
My question is now, if it is a problem to collapse the categories of these items because they become more difficult as they really are (especially in comparison to the few items where collapsing is not nessecary). My primary concern is to get stable measures of the persons (the item hierarchy is not so important)
MikeLinacre:
You want "stable measures of the persons", RLS.
This means that we need category-collapsing that is not influenced by accidents in the data. That is the purpose for the "at least 10 observations" guideline.
Collapsing the categories makes those items more robust.
As we collapse categories, we expect the reported item difficulty to change. This can be overcome (for reporting purposes) by "pivot anchoring" the items. See
https://www.winsteps.com/winman/index.htm?safile.htm
and
https://www.rasch.org/rmt/rmt113e.htm
RLS:
Thanks a lot, Mike! Because of your help I can continue to work.
742. Is Rasch nested in the GPC model?
rblack June 18th, 2009, 2:04pm:
Hi,
I'm trying to compare overall fit of the Rasch Model to the overall fit of the Generalized Partial Credit Model on the same data. Is the Rasch model nested in the Generalized Partial Credit Model? I ask because I'd like to conduct a Chi-Square test on difference in -2LLs with df=difference in # of parameters estimated. If they are not nested, is it acceptable to compare the -2LLs without running a formal test? Any other ways to test differences in *overall* model fit?
Any help would be greatly appreciated.
Thanks,
Ryan
MikeLinacre:
Thank you for your question, Ryan.
The Rasch (Masters) Partial Credit Model is nested within the (Muraki) Generalized Partial Credit Model. The Muraki (1992) model has a discrimination parameter for each item. The Masters (1982) model has a shared discrimination for all items.
So the difference in parameters is (number of items - 1).
rblack:
Dear Mike,
Thank you so much for replying. If I may, I'd like to ask a follow-up question.
I noticed that you stated that the df = # of items -1, but that is not what I'm seeing in a book called item reponse theory for psychologists. The book states that when testing for overall fit between the rasch partial credit model and the generalized partial credit model that df=# of additional parameters, and in their example the # of additional parameters = # of items, not # of items-1.
Here's a link:
http://books.google.com/books?id=rYU7rsi53gQC&pg=PA113&lpg=PA113&dq=item+response+theory+for+psychologists+generalized+partial+credit+model+log+likelihood+value&source=bl&ots=ZAFQCeae5O&sig=fmJ2XOMIRrnHpNlu_cB1W9xkk0M&hl=en&ei=OCQ8SryjB8yJtgfMn5gW&sa=X&oi=book_result&ct=result&resnum=1
The sentence starts at the bottom of page 114 (note this model has 12 items and df=12).
I hope you have time to respond.
Thanks again,
Ryan
MikeLinacre:
Rblack, there must be constraints on the item discriminations in the GPC estimation. Here is a thought-experiment ....
Imagine we estimated a one-item Rasch PCM and a one-item GPC.
The Rasch discrimination would be constrained to be 1.0
The GPC discrimination would be constrained to produce a sample S.D. of 1.0
So the two models would have the same d.f.
Two items: GPC now has one less d.f.,
L items: GPC now has L-1 less d.f.
Further, in one GPC program there are two constraints on discrimination for L items: log-discrimination mean and s.d. , so that GPC has L-2 less d.f.
How many constraints does your GPC program place on item discrimination estimates?
rblack:
Thank you for continuing to help me. Much appreciated.
I see the point you make in the previous message. Thank you for the clarification. I am not sure how many contraints are placed on the GPC model I'm running in PARSCALE. I will look into this further and get back to you. Out of curiousity, was the GPC program to which you were referring PARSCALE?
It sounds like df could equal (# items-1) or (# of item-2) depending on the number of constraints, but having no constraints is not possible (i.e. df=# of items). I wonder how the authors ended up with df=# of items. Perhaps their rasch or gpc analyses were done differently in some way.
Thanks,
Ryan
MikeLinacre:
Oops, Ryan! Sorry, I have been writing this backwards. Generally:
Degrees of Freedom = Number of data points - Number of "free" parameters
So GPC has (items# - 1) or (items# - 2) d.f. less than Rasch PCM.
I believe PARSCALE constrains the item discriminations to have a log-normal distribution, so this would be two constraints (items#-2). It also means that an item discrimination cannot go negative, even when the item's point-biserial is negative.
rblack:
Hi Mike,
Thank you so much for your help. This definitely makes sense to me. I hope it's okay, but I have just one more question. I'm trying to obtain the -2LL from the rasch partial credit model in the Winsteps output, and would like a clarification.
Is the "log-likelihood Chi-Square" value equal to the -2LL, or should I?:
2*log-likelihood Chi-Square
Thanks again for all your help!
Ryan
MikeLinacre:
Ryan, "log-likelihood Chi-Square" means "the Chi-Square calculated using the log-likelihood" = - 2 * log-likelihood of the data.
rblack:
Thanks for all your help, Mike!
743. i m confuse
bahar_kk June 21st, 2009, 9:05pm:
hi every body
i have some question, do u know ,
what is Mont carlo simulation ?
what is its different with IRT software(Bilog,wingen,..)?
i need data to use neural network and IRT software,because i want to implement Neural network to estimate ability and parameters of IRT
then compare NN va IRT together ,
how do i generate Data set??
please guide me.
MikeLinacre:
Monte Carlo simulation is used to produce artificial data which has a random component.
it is usually not complicated to do.
1. Choose the model you want the data to fit.
2. Choose some parameter values.
3. Apply the parameter values to the model to generate the data.
For instance, for the dichotomous Rasch model:
Person ablity = 1
Item difficulty = 0
Apply Rasch model: expectation = exp(1-0) / (1+exp(1-0)) = 0.73
Probabilities have the range 0-1,
Generate a random number U[0,1] = .593 (say)
.593 is less than .73 so simulated data value is "1".
For polytomous data, see https://www.rasch.org/rmt/rmt213a.htm
744. SD of theta distribution
herethere June 19th, 2009, 1:40pm:
When I set UPMEAN = 0 and USCALE = 1, why did I get the SD of the theta distribution not equal to 1 (in my case, I got SD=1.22)?
Thanks!
MikeLinacre:
Herethere, USCALE= rescales logits. It does not set the S.D.
For your S.D. to be 1.0, please specify USCALE = 1/1.22 = 0.82
herethere:
Mike, thanks for your answer. Do you mean that I have to have two runs if I want to fix the theta distribution to have a mean 0 and SD 1: the first run sets UPMEAN = 0 and USCALE = 1, and the second run sets UPMEAN = 0 and USCALE = 1/(whatever SD value I got from the first run)? Is there a way that I can set the mean and SD of the theta distribution to some specific values in just one run?
Thanks!
MikeLinacre:
Sorry, Herethere, two runs are required ...
But usually the first run is repeated several times as we fine-tune the analysis. The second run is once or twice for the final output
745. specify the number of quadrature points
herethere June 12th, 2009, 8:01pm:
Can I specify the number of quadrature points in WINSTEPS? WINSTEPS will give me the theta value for each person, and I can use EXCEL to find the distribution of theta, but the numbers of qudrature points vary from one sample to another. If for some reason I want the two samples to have the same numbers of quadrature points, say, 40, how can I do that with WINSTEPS?
Thanks!
MikeLinacre:
Thank you for your question. Herethere.
Quadrature points are used in some computational techniques, usually for numerical integration. Winsteps does not use quadrature points.
Perhaps you are looking at the posterior distribution of the person sample. In Winsteps, this is computed based on one estimate for each different person raw score, so there are as many estimation points (quadrature points?) as there are different raw scores. This behavior cannot be changed.
An estimation method which does use quadrature points to model a smooth posterior sample distribution is Marginal Maximum Likelihood Estimation (MMLE). This is implemented in ConQuest and other Rasch programs, see www.winsteps.com/rasch.htm
herethere:
Thanks for your reply!
746. Adhering to Principles of Measurement When Designi
pjiman1 June 2nd, 2009, 2:58pm:
Adhering to Principles of Measurement When Designing Assessments for summative, screening, formative, evaluative and research purposes
I have been reviewing scales and the question I have is does the measurement model change as a result of the purpose of the scale? In my field of social and emotional learning, we want measures that do a variety of tasks - Screening of kids, monitoring of kids progress, epidemiological assessment, formative assessment, accountability, evaluation of programs, research, and for use in consultation. From my review of the literature in my field, I believe that there is an underlying assumption emanating from the field that there should be different measures for each of these purposes. I contend that whenever you are measuring something, no matter the purpose, the principals of measurement - invariance, ordered objects and units, established origin, equi-distant intervals of measurement units, conjoint additivity, etc. - stay the same no matter the purpose of the scale.
In many measurement instances, the scale stays the same. For example, whether or not you are measuring the number of yards a person can throw a football, the length of a wall, or the height of Mt. Everest, a foot is still a foot, a yard is still a yard, an inch is still an inch. The scale works no matter what is being measured for a specified purpose.
In my field of social and emotional learning for children, various organizations state that their psychological assessments are suited for some or many purposes. Chief among these purposes are: screening, formative, evaluative, and research. When I work with an organization that wants to design, select, or evaluate a set of assessments for these purposes, I sense from them that they assume that the scale content, items, and rating scale will differ depending on the purpose of the assessment. It's as if a psychological assessment will have a different set of items, rating scales, and content, depending on if you are using the assessment for a screening, formative assessment, or as part of a research project evaluation.
I contend that it is how we adapt the scale and use it use the scale that differs. For example, we use a 4 foot cutoff line to screen if certain kids are tall enough to ride a roller coaster, we use the ruler to decide if one person throws a football for more yards than another person, we use a ruler to determine how tall a person is growing based on a diet plan. In assessments of latent constructs, such as emotional competency (my assessment area) the same situation occurs. For example, in a screening assessment, you establish cut off scores and expected zones for misclassification error for emotional competency; those above the cut off score get no treatment, those below get treatment. In a formative assessment, you obtain scores that involve the participant in a discussion of the score and next steps for learning and improvement. In an evaluation or a research project, you obtain the scores and compare it to established norms to make a determination about the participant. In each of these cases, the scale content, i.e. the items and their rating scales, does not change, it's how we use or contextualize the results, that is, the actual scores obtained from the scale, that change.
If there is one thing that may change depending on the purpose of the scale, it is the item content and the number of items. In physical measurement, to screen kids� height for a roller coaster ride, all we need is one mark - a 4 foot line - to make this measurement. To measure kids� height after a diet and exercise plan, we need more units (e.g. more feet and subdivisions into inches) because it is this kind of precision we need to detect an effect of the intervention. In both cases, the measurement units, e.g. feet, stay the same, we just divide them differently based on need.
It seems that in general, for latent psychological constructs, the content of the items range broad to specific. To measure emotions, we can indicate the presence of the four basic emotions - happy, mad, sad, scared. If we need to, we can generate more items that are broad or specific - happy, ecstatic, content, elated, pleasant. The key phrase to me is �if we need to.� If we want to conduct a broad screening assessment of students within a school, say the % of kids who report experiencing depression, we may need just the four items about the four basic emotions (plus a few more to increase reliability). That information may be enough for a broad assessment. For an assessment to detect the effects of an intervention, we may need specific items and more of them so we can detect how kids are progressing along the dimensions for the four basic emotions.
The reason I want to clarify this is to demonstrate what actually changes when we create measurements for different purposes. No matter the purpose, the measurement principals stay the same. The item difficulty, the specificity of the item, and the number of items may differ because the purpose of the measurement changes. The measurement usually changes depending on if the need for the resulting scores obtained from the measurement is for broad or specific uses. It's not as if you can construct an item and say it is strictly for a behavioral screening, for a formative assessment, or to detect experimental change.
In the end, based on the principles of measurement, items will still be calibrated on an ability parameter, that is, on a range from easiest to hardest. No matter the item, whether a broad or specific item, if the item is a difficult one to endorse, it is on the upper end of the scale, if it is easy, it is on the lower end of the scale. The purpose of constructing items and developing scales is to further understand different parts of the measurement continuum. Measures can be used to expose abnormalities in the data. I am reminded of a quote by Ben Wright (1996, p. 3) and Mark Stone (2004, p. 218) - "All that can be observed is whether or not the specified event occurs, and whether the data recorder (observer or respondent) nominates (any particular) category as their observation." In human science measurement, all we can do is see if a person endorses an item or if a rater determines if the item reflects what he or she is observing. This act of measuring does not change, no matter the purpose of the measurement.
The next section below contain examples of various social emotional assessments. I have underlined the assessment�s stated purpose. If you look at the assessment examples, you'll see that despite the purpose and content area, the scale items are similar and the rating scales are similar. It makes me wonder, as I reflect on the principles of measurement, how different these assessments are from each other, despite the differences in their stated purposes.
Mike, I welcome your thoughts about my current line of thinking. Am I on the right track here regarding the intersection between the principles of measurement, how measurements are constructed and the purpose of measurement?
Thank you,
Pjiman1
------------------------------------------
Assessment Example 1. Teacher Rating behavioural screening questionnaire about 3-16 year olds. It exists in several versions to meet the needs of researchers, clinicians and educationalists.
Directions: For each item, please mark the box for Not True, Somewhat True or Certainly True. It would help us if you answered all items as best you can even if you are not absolutely certain. Please give your answers on the basis of the child's behavior over the last six months or this school year.
Item Not true Somewhat true Certainly True
1. Considerate of other people�s feelings
2. Often loses temper
3. Shares readily with other children,
for example, toys, treats, pencils
Assessment Example 2. Researchers from xxx are developing a new set of strength-based social-emotional assessments for children and adolescents. The xxx is being designed as cross-informant measures of students' assets and resilience, taking into account problem-solving skills, interpersonal skills, the ability to make and maintain friendships, the ability to cope with adversity, and the ability to be optimistic when faced with adversity. Our goal for these measures is to help move the field of behavioral, social, and emotional assessment more into the realm of strength-based assessment, as a balance to the historical focus on assessing problems or psychopathology. When completed, the xx is intended to be used for screening, assessment and decision making, intervention planning, intervention monitoring and evaluation, program evaluation, and research.
Directions: Here are xx items that describe some positive social and emotional characteristics of students. Please rate how true you think these items have been for this student during the past 3 to 6 months. Circle N for NEVER true, or if you have not observed that characteristic. Circle S for SOMETIMES true. Circle 0 for OFTEN true, and circle A if you think the item has been ALWAYS or ALMOST ALWAYS true for this student during the past few months.
item N S O A
1. Likes to do his/her best in school
2. Feels sorry for others when bad things happen to them
3. Knows when other students are upset, even when they say nothing
4. Stays calm when there is a problem or argument
5. Is good at understanding the point of view of other people
Assessment Example 3 - Grades K through 8. The XXX, provides a measure of social-emotional competencies, which can be used to promote positive youth development. The XXX 1) provides a psychometrically sound, strength-based, measure of social-emotional competence in children and youth, 2) Identifies children and youth at risk of developing social-emotional problems before those problems emerge, 3) Identify the unique strengths and needs of individual children and who have already been identified as having social, emotional, and behavioral concerns, 4) Provide meaningful information on child strengths for inclusion individual education and service plans as required by federal state and funder regulations, 5) Facilitate parent-professional collaboration by providing a means of comparing ratings on the same child to identify similarities and meaningful differences.
Directions: During the past 4 weeks, how often did the child N S O F VF
1. Remember important information
2. Carry him/herself with confidence
3. Keep trying when unsuccessful
4. Handle his/her belongs with care
5. Say good things about him/herself
Assessment Example 4. Behavioral and Emotional Screening System , teacher form, Grades K-12
Designed for screening behavioral and emotional strengths in children and adolescents from preschool through high school. Used by schools, mental health clinics, pediatric clinics, communities and researchers for screening. Quick evaluation of all children within a grade or school, early identification of problems, standardized way of identifying students who have a high likelihood of having behavioral or emotional problems.
Directions: mark the response that describes how this student has behaved recently in the last several months
Item Never Sometimes Often Almost Always
1. Pays attention
2. Disobeys
3. Is sad
4. Breaks Rules
5. Is well organized
Assessment Example 5. Development of a formative assessment for social and emotional competencies.
Social and emotional Goal: Develop Self Awareness and self-management skills to achieve school and life success
Item: Identify and manage one's emotions and behavior
Rate the student if he or she can...
a) describe a physical response (e.g., heart beating faster, trembling etc.) to the emotion of basic emotions (e.g., happy, sad, angry, afraid, )
b) describe how various situations make him/her feel
Rating scale:
Score 4.0 In addition to Score 3.0, in-depth inferences and applications that go beyond what was taught.
Score 3.5 In addition to score 3.0 performs in-depth inferences and applications with partial success.
Score 3.0 The student exhibits no major errors or omissions.
Score 2.5 No major errors or omissions regarding 2.0 content and partial knowledge of the 3.0 content
Score 2.0 There are no major errors or omissions regarding the simpler details and processes as the student: However, the student exhibits major errors or omissions regarding the more complex ideas and processes.
Score 1.5 Partial knowledge of the 2.0 content but major errors or omissions regarding the 3.0 content
Score 1.0 With help, a partial understanding of some of the simpler details and processes and some of the more complex ideas and processes.
Score 0.5 With help, a partial understanding of the 2.0 content but not the 3.0 content
Score 0.0 Even with help, no understanding or skill demonstrated.
MikeLinacre:
Thank you for sharing your ideas, Pjiman1. It will take me a few days to mentally digest them .... :-)
pjiman1:
Thanks Mike, I always appreciate your insights. Sorry if my post was turgid, but I appreciate your efforts to help me untangle my thoughts.
pjiman1
Stampy:
This is a very interesting discussion. I'm involved in second language proficiency assessment, and we face the same issue of multiple potential uses for language proficiency data. We can imagine uses such as placement of students into classes, determining readiness for study abroad, "testing out" of foreign language requirements, verifying language proficiency for teacher certification, etc.. If one had a calibrated bank of "language proficiency" items, it seems that one should be able to construct multiple tests from this bank for different purposes, picking and choosing those items that are most appropriate for the decision in question.
I think one of the issues has to do with the "level of scale" on which the test needs to operate. When I'm conceptualizing "second language reading proficiency", I recognize that it is an ability that includes many subcomponents: grammatical knowledge, discourse knowledge, vocabulary knowledge, strategic competence, and so on. Even so, I can conceptualize a single continuum of reading ability along which people can be more or less proficient (perhaps due, in some part, to their ability to deploy those various component skills). As a practical matter, I know that the "reading" items on my test may be tapping into slightly different aspects (component skills?) of reading proficiency from one another. An item that (primarily) taps into vocabulary knowledge can be a "reading" item in the company of other "reading" items (tapping into the myriad of subskills that make up reading), but a "vocabulary" item in the company of "vocabulary" items.
Perhaps in this way, items can be said to have an "essential character", yet the meaning of groups of items can be differen. I don't know if this is similar to your situation.
pjiman1:
Thanks Stampy for your input. I believe your thoughts are in concert with mine. When people talk about assessment, they talk about it in terms of summative, formative, criterion, evaluation, monitoring, screening, accountability, and as if there are different properties for each type of assessment. In some way, perhaps the difficulty and the specificity of the items might be different, the way items are grouped together might be different. But in the end, for a given set of items, all of the aforementioned purposes of assessment still have to follow the basic principles of measurement - linear measures, the items and objects can be reliably placed in order along the measurement line and equal interval units of measurement, etc. A thermometer is still a thermometer no matter what use we have for the scores that are generated from a measurement event.
747. Rasch model & Screening tests
RS June 12th, 2009, 4:17am:
Dear Mike
I have received data from a comprehensive screening test with 120 items. This test is appropriate for the screening of the 15 most prevalent psychological disorders in children and adolescents. This instrument consists of three forms: 1) self-report form, 2) teacher form and 3) parent or carer form.
Is there any way to use Rasch model to analyse the data from this test which is designed to screen a wide range of psychological disorders?
Many thanks and regards
RS
748. Category scales and the 'hill' curves
bahrouni May 23rd, 2009, 6:45am:
Hi Mike,
I am using MFRM to analyze the analytic rating of 3 EFL essays by 56 raters. I'd like to look at the impact of the raters' backgrounds on their way of rating. I have divided the raters into three groups as you suggested in an earlier posting: 1) native speakers, 2) Arabic speakers (who share the students' L1 + culture) and 3) other: non-native & non-Arabic speakers.
The essays are assessed on 4 categories: Task achievement, Coherence & Cohesion, Voc. and Gr. using a 25-point scale to get the total raw score out of 100 (4x25).
The problem I have faced is that on entering the raw scores (rounded up: no decimals) as they are out of 25, I had messy scale curves; I mean those hills for the different scores have no separate peaks. Add to this, the numerical values are different from the ones entered. Please see the attachement (25-pnt scale) to have a clearer idea of what I am talikng about.
Earlier in a pilot analysis, I had the same problem. Professor James Dean Brown, who had introduced me to MFRM, was around for our conference, so I had a chance to show him the results from my pilot analysis and asked him about that problem. He suggested that I should make the scale smaller. So I divided the scales by 5 so as to have a 5-point scale for each of the categories. It worked well.
When I tried the same thing this time, it has also worked well but I have noticed the following:
1) the vertical ruler is much longer than the 25-point scale.
2) the measures are not the same: the logit scale does not show the same measures for the most severe/lenient raters; the most/least able students; the most difficult/easiest category.
Please see the attachment (5-pnt scale) to compare it to the 25-pnt one.
I have also noticed that when dividing the initial raw scores (out of 25) by 5 and round them up, it takes 2.5 points to move from K-1 to k up the scale. For example all the raw scores between 7.5 and 12.49 out of 25 are equal to 2 out of 5; those between 12.5 and 17.49 out 25 are 3 out of 5, etc.. This has made feel that this dividing issue is making the analysis less sentive to differences between the abilities.
Is there another way of doing it?
Thanks a lot for your help
Bahrouni
MikeLinacre:
Thank you for sharing your analysis with us, Bahrouni.
You write: "I have divided the raters into three groups as you suggested"
Comment: Yes, you have done this. But did you notice at the end of Table 3: "Warning (6)! There may be 3 disjoint subsets" and in Table 7 "in subset: 1"?
Your Rasch measurement model is not sufficiently constrained. It is �unidentified�.
In your earlier post, you talked about "bias analysis". This requires:
Labels=
....
*
3, Background, A ; anchor to make this a dummy facet, only used for interactions and fit.
1=Native, 0
2=Arab,0
3=Other,0
*
You write: Model =?B,?B,?,#,R25
Comment: You are doing two exploratory analyses at the same time. This is sure to be confusing. Please try this:
Analysis 1. Investigate "examinee x background" interactions:
Model =?B,?,?,?B,R25
Analysis 2. Investigate different rating scale usage for different backgrounds:
Model =?,?,?,#,R25
Analysis 3. Investigate "examinee x rater" interactions. (The data are probably too sparse for this).
Model =?B,?B,?,?,R25
You write: "as they are out of 25, I had messy scale curves;"
Comment: Yes, this is the usual situation when the rating scale has more categories than the raters can discriminate. The frequencies of the rating-scale categories become uneven, and the category probability curves look messy.
You write: "1) the vertical ruler is much longer [for the 5-point scale] than the 25-point scale."
Comment: Yes. This confirms the finding that the categories on the 25-point scale are largely accidental. The raters are not able to classify performance into 25 levels, so they choose minor differences in ratings at random or idiosyncratically.
You wrote: "2) the measures are not the same:"
Comment: Yes, we expect this. Look at Table 8. You have three rating scales, with a different range of categories in each scale. This is certain to be confusing to your audience. Consequently only use "#" in your Model statement to investigate use of the rating scale, not for investigating the measures.
You wrote: "this dividing issue is making the analysis less sensitive to differences between the abilities."
Comment: Yes. The re-categorization has lost too much measurement information. Under these circumstances, we need to find the categorization which has the most useful information relative to the rater idiosyncrasy.
Look at 25-point Table 8. Inspection of the category frequencies and the "average measures" suggests what may be a better re-categorization for your data.
You have 4 rating scales in Table 8, so this is somewhat complicated. Please investigate combining categories in an analysis with only one rating scale (Analysis 1). For the rating scale consisting of combined categories you need:
(1) at least 10 observations for each combined category
(2) the average measures of the combined categories to advance noticeably.
OK?
bahrouni:
Hi Mike,
Thank you very much for replying and clarifying things to me.
1) I noticed that warning (6) but did not pay much attention to it because I thought it was not all that important. I've fixed it and now it reads 'subset connection O.K.'
2) In your posting, you focused more on the 25-point scale. Does this mean you discourage me from using the 5-point scale because 'much of the measurement information' is lost there, and it is complicated to combine the categories in one scale, which I have not understood anyway?
3) You have mentioned 3 scales in Table 8 that could help suggesting 'a better re-categorization for my data.' Could you please be more precise. I think anxiety has turned me so blind that I could not see these 3 scales!
4) If the worst comes to the worst and went on with the 25-point scale and explained the extent to which the raters have failed 'to classify the performances into the 25 levels' of the scales based on what those 'messy' frequency curves show, wouldn't that have an adverse effect on the analysis?
5) You have finally asked me to investigate combining categories. Where should I start? Honestly, I have no clue about this.
Once again thank you for your invaluable help and your bearing with me.
Bahrouni
MikeLinacre:
Thank you for response, Bahrouni.
1) Yes, subsetting is not important if you are only concerned about fit and interactions. But you commented on the measures "changing". Subsetting does alter the measures.
2) From a measurement perspective, the 5-point scale is definitely better than the 25-point scale. But your results indicate that perhaps a 7-point or 8-point scale would be even better
3) Sorry, I did not read your original analysis carefully. You have put # for "category". This has produced 4 rating scales. You can see them in Table 6, and also Tables 8.1, 8.2, 8.3, 8.4.
4) The 25-point Rasch analysis is better than a raw-score analysis, but why do we perform Rasch analysis? One reason is that we want to make better inferences from our data. The "messier" the data, the less secure are our inferences.
5) Combining-categories is a technical area of Rasch analysis. It is a feature of many Rasch papers. There are some suggestions at www.rasch.org/rn2.htm
bahrouni:
Hi Mike,
Thank you for responding to my enquiries.
Here's what I've done:
I've worked out 2 scales: a 7-point scale and an 8-point one by dividing the obtained score over 25 and multiplying the result by 7 and 8 respectively. The results are handsome. I am quite happy with the analysis, and I will gladly and gratefully share them with you in the attachments herewith. I can see slight diffrences between the two scales, and I think I'll go for the 7-point scale because I have found that it spreads the ruler slightly more than scale 8.
However, my question this time is related to the bias analysis. I ran the analysis for the interaction between the Background (facet 3) and the categories (facet 4):
One of my null hypotheses is that raters' background has no effect on their assessment of the categories.
When I look at the Background Measurement Report (with reference hereafter to scale 7), I find that the logit meaure is 0 and the Chi Square is also 0 with a d.f. of 2 and a probability significance of 1:00 (way above .05), which means that the difference between the backgrounds is very insignificant, so the null hupothesis is proved, and therefore it should be retained.
On the other hand, when I look at the Bias/Interaction Calibration Report, I find that there are 12 bias terms, and the Chi Square here is 11.7 d.f.:12 with a probability significance of .47 (above .05), which also leads to proving and retaining the null hypothesis.
Question: Aren't these 12 bias terms an indication that raters' background has some influence on the way they rate these categories?
Thank you
Bahrouni
bahrouni:
Hi Mike,
Sorry, here's the 2nd attachment.
Thank you for responding to my enquiries.
Here's what I've done:
I've worked out 2 scales: a 7-point scale and an 8-point one by dividing the obtained score over 25 and multiplying the result by 7 and 8 respectively. The results are handsome. I am quite happy with the analysis, and I will gladly and gratefully share them with you in the attachments herewith. I can see slight diffrences between the two scales, and I think I'll go for the 7-point scale because I have found that it spreads the ruler slightly more than scale 8.
However, my question this time is related to the bias analysis. I ran the analysis for the interaction between the Background (facet 3) and the categories (facet 4):
One of my null hypotheses is that raters' background has no effect on their assessment of the categories.
When I look at the Background Measurement Report (with reference hereafter to scale 7), I find that the logit meaure is 0 and the Chi Square is also 0 with a d.f. of 2 and a probability significance of 1:00 (way above .05), which means that the difference between the backgrounds is very insignificant, so the null hupothesis is proved, and therefore it should be retained.
On the other hand, when I look at the Bias/Interaction Calibration Report, I find that there are 12 bias terms, and the Chi Square here is 11.7 d.f.:12 with a probability significance of .47 (above .05), which also leads to proving and retaining the null hypothesis.
Question: Aren't these 12 bias terms an indication that raters' background has some influence on the way they rate these categories?
Thank you
Bahrouni
MikeLinacre:
Thank you for sharing your bias/interaction analysis, Bahrouni.
A. All your "background" elements are anchored at 0, so there cannot be a 'background" effect for that facet.
If you want to see if the mean leniencies of the different backgrounds are different, please add a "group" indicator to the elements in facet 2:
Labels=
2, Raters
1 = Native Rater1 , 1 ; 1 is the group for the native raters
...
*
There will be a separate subtotal for each group.
B. The 12 bias terms in Table 13.1.1 have a size approximating their standard errors, and they are not statistically significant. They have the randomness we expect for a fixed effect (no bias) measured with the precision that these data support.
There is no statistical evidence for a "background x category" interaction.
OK, Bahrouni?
bahrouni:
Thank you Mike.
I have the weekend ahead of me to make the change in facet 2.
I'll get back to you when that is done.
Once again thank you very much.
Bahrouni
bahrouni:
Hi Mike,
Following your instructions, I have made the following change, (1 = Native Rater1, 1; 1 is the group for the native raters...) to Facet 2, but it has produced no change in the tables, rather I haven�t been able to see the differences, if any!
a) Have I made the right changes properly in the right place?
b) My focus is on the interactions between facets 3 and 4, I mean I want to look at the way(s) each of the backgrounds treats the 4 categories = Do teachers from the 3 different backgrounds score those 4 categories in the same way? May I ask you to kindly look again at the attached �new� file (with the suggested change) and tell me where FACETS subtotals each of the groups separately, or tell me if I have made a mistake.
c) The ruler, the background statistics and the interaction statistics altogether confirm the Ho that the three backgrounds score the 4 categories in a quite similar way. These statistics do not reflect the reality!! Could this be another confirmation of what McNamara found in 1996: Raters thought they were doing something but Rasch showed they were doing something totally different? Or is it a mistake I have made somewhere or a misinterpretation of the results?
New Question: Infit high and low limit values
You have often been quoted saying that �there are no hard-and-fast rules for setting
upper- and lower-control limits for the infit statistics.�
Most researchers have followed Pollitt and Hutchinson�s (1987) suggestion: a value lower than the mean minus twice the standard deviation would indicate too little variation, lack of independence, or overfit. A value greater than the mean plus twice the standard deviation would indicate too much unpredictability, or misfit. When I look at my raters� measurement, I see that the mean is .99 and the SD is .59.
Therefore my infit upper limit should be:
.99 + (.59x2)
=.99 + 1.18
= 2.17
While the lower limit should be
= .99 - (59x2)
� � = .99 = 1.18
= -.19
We know that the Infit MnSq does not have negative values, is it safer then to look at the same values (between -.19 and 2.17) in ZStd? I say the same values because if do the same calculations for the ZStd, I will end up by having the following �unacceptable� limits:
-2+ (1.5x2)
= -2 +3 = 1
While the lower limit will be
(-2) - (1.5x2)
= (-2) - (3) = -5
Please bear with me.
Thank you
MikeLinacre:
Thank you for your question, Barouni.
My apologies for the delay in responding to your post. By now you have probably answered most of your question for yourself, better than I could do it.
Advice such as "a value lower than the mean minus twice the standard deviation would indicate too little variation, lack of independence, or overfit." implies that the underlying numbers are linear.
Mean-squares are geometric. So, you would apply that rule to log(mean-square).
bahrouni:
Good morning Mike,
Thank you for your response. Now I can go on with the discussion of the results with much more confidence.
I'll definitely come back to you if something comes up my way.
God bless you
Bahrouni
749. Difference between WinSteps and RUMM 2020
Per_aspera_ad_astra May 15th, 2009, 12:20pm:
Dear Mike and all Rasch experts,
I'm an Italian student of Psychology. I'm working for my graduation thesis in Psychometry, about Rasch Model, and I'm looking for some informations about the difference between WinSteps and RUMM 2020.
I read in this forum and in "The Matilda Bay Club" one every discussion about this topic, but I'm very inexperienced and so I hope that you can explain me in plain words why these software give different outcome from the same data.
Thank you.
P.S. I'm sorry for my bad english!
MikeLinacre:
Thank you for your question, P-a-a-a.
There are technical differences between Winsteps and RUMM2020. For instance, they use different estimation techniques and compute their fit statistics slightly differently. The different computations have advantages and disadvantages, but usually produce results that are almost identical for practical purposes. There are also considerable differences in the input and output data formats, and the operation of the software by the analyst.
But it is not usually the differences in the numbers that produce different outcomes. It is the differences in the measurement-philosophies of the analysts using the software. Winsteps and RUMM2020 operationalize different approaches to Rasch analysis. RUMM2020 is more concerned about the fit of the data to the chosen Rasch model. Winsteps is more concerned about the usefulness of the Rasch measures. These different philosophies cause the analysts to choose different numbers to report, and also to make different decisions based on those numbers.
Forum members, please tell us your own answers to P-a-a-a's intriguing question.
Per_aspera_ad_astra:
Thank you, Mike
your answer is very clear, and I know how many I still have to learn about Rasch Model, but I would like to ask you two more detailed quetions:
"they [WinSteps vs. RUMM 2020] use different estimation techniques and compute their fit statistics slightly differently".
1. Can you explain me what does different estimation techniques consist of? I read contrasting informations about this topic.
2. More specifically: is due the difference to a joint estimation that RUMM 2020 use to process its outcome?
I think may be it's so because in a little work I found that the RUMM 2020 program gives different results for items having the same score in WinSteps. That can be due to the estimation of the difficulty taking into account the person ability, but, if I do right, this fact is contrary to a characteristic of the Rasch Model, that is that the ability and the difficulty are mutually independent.
Thank you for your helpfulness!
MikeLinacre:
Thank you for your questions, P-a-a-a.
RUMM2020 uses Pairwise Maximum Likelihood Estimation (PMLE). Winsteps uses Joint Maximum Likelihood Estimation (JMLE). Since the data are generated by both the person abilities and the item difficulties, all estimation methods must adjust for person abilities when estimating the item difficulties, and adjust for the item difficulties when estimating the person abilities.
In PMLE, every pair of items is examined, and the counts of persons who succeed on one item and fail on the other item are obtained. These counts are the sufficient statistics from which the Rasch item-difficulty measures are estimated. Once the item difficulties have been estimated, the person abilities are estimated using a method similar to https://www.rasch.org/rmt/rmt102t.htm.
In JMLE, the raw scores for the persons and the items are the sufficient statistics from which the Rasch measures are estimated. This is equivalent to applying https://www.rasch.org/rmt/rmt102t.htm to both the persons and the items simultaneously.
Because the estimation methods differ, the estimates also differ. But the differences are usually much smaller than the standard errors (precisions) of the estimates.
RS:
Hi Mike
Please correct me if I am wrong.
You wrote: �Winsteps and RUMM2020 operationalize different approaches to Rasch analysis. RUMM2020 is more concerned about the fit of the data to the chosen Rasch model. Winsteps is more concerned about the usefulness of the Rasch measures. �
In order to evaluate the usefulness of the Rasch measures, the first thing that needs to be done is to analyse the fit of the data to the chosen Rasch model by using item and person fit statistics. Fit analysis results provide some idea about the validity of your scale and consequently present some thought about the usefulness of using the measures produced by this scale.
Given this, in a Rasch analysis the main concern should be whether or not you data fit the chosen Rasch model.
Regards
RS
MikeLinacre:
You are correct, RS. We always want valid tests, particularly construct validity (does the test measure what we intend it to measure) and predictive validity (does the test predict the results we expect it to predict). If a test lacks these two validities, then it is (or will be) useless for our purposes.
A testing agency had a test with great predictive validity, but it lacked construct validity. The test "worked" (no one knew why) until the day that it didn't. And, because they didn't know why it worked, they failed in their efforts to produce a revised test that worked.
But "fit" is much less certain. There are two types of fit:
1. "The data fit the model (statistically perfectly)" - this is the conventional hypothesis test.
2. "The data fit the model (well enough for practical purposes)" - this is the test that cooks use when selecting vegetables for the stew.
The European Union tried to apply a "type 1" approach to vegetables - with ridiculous results:
http://www.independent.co.uk/news/world/europe/ugly-fruit-and-veg-make-a-comeback-1015844.html. If the "vegetables didn't fit the model of a perfect vegetable, they could not be sold".
Winsteps is aimed at rescuing as many nutritious (useful) vegetables as possible, even if they are the wrong color or shape (don't fit the model of a perfect vegetable).
connert:
Interesting analogy Mike. I would add a third category and that is people who are so concerned with statistical fit that they give up measurement properties of the model (and hence validity) by adding parameters. A clearer understanding of validity would lead you instead to change items and circumstances of administration. I use fit statistics to improve items and choose items and see that as their primary function. It is a good way to poke holes in your original theoretical basis for constructing items.
RS:
Thanks a lot Mike .
I agree that asking whether or not the data fit the model is, in fact, the wrong question. The truly significant question is, �Do the data fit the model well enough to suit the purpose?� Such a refocusing of the question acknowledges that fit to the model is a relative concept: nothing fits perfectly. In order to answer the question about data-fit to the model, it is important to examine the consequences of misfit.
Given this, when data fit the Rasch model the usefulness of the measures is almost guaranteed. However, more investigation is necessary as model-data fit gets progressively worse.
Regards
RS
MikeLinacre:
RS, you go half-way: "when data fit the Rasch model the usefulness of the measures is almost guaranteed"
Yes, but useful for what? We go back to your remark about validity. It is the construct validity and the predictive validity which tell us.
For instance, we can simulate data which fit the Rasch model. They are useful for some purposes, such as investigating the functioning of a Rasch estimation algorithm, but they are useless for other purposes, such as measuring the "ability to do arithmetic".
The data of a Certification Examination had reasonable fit to the Rasch dichotomous model, but, on closer inspection, the items looked like a game of Trivial Pursuit - a grab-bag of specialty facts. The construct (latent trait) underlying the Examination seemed to be "degree of specialty obscurity", and its predictive validity seemed to be "exposure to unusual specialty situations". This was not the intended latent variable. The intended latent variable was "mastery of typical situations".
msamsa:
thank you all
750. Rescaling
siyyari June 4th, 2009, 10:46am:
Hi Dr. Linacre,
My thanks for the previous reply.
As I told you before, my original scoring of the sample was on a Likert scale ranging from 1 to 5. After the Rasch partial credit analysis by FACETS, I want to modify the intervals of the likert scale based on the achieved difficulty estimates for each category score. If I use Table 6, I cannot find the equivalent logit values for each category score within the range 1-5 on the likert scale, so I guess I should use another table to find the difficulty values of reaching each category score on the likert scale. My own guess is the use of Expectation Measures at Category column in table 8.1, and then doing a linear transformation like the one explained in the manual (i.e., 7.46. Umean (user mean and scale) = 0, 1Improving Communication).
Is my guess right?
If not, how can I modify the distances between my original scale�s category scores based on the logit values?
Hope I could convey my point to you.
MikeLinacre:
Siyyari, are you looking for values which are closer to linear than the original rating scale category values?
If so, Facets Table 8 "EXPECTATION measure at category" are the values you want.
If your data does not contain observations of category 1, you need to construct a reasonable "dummy" data record which does contain category 1 (and some other categories), and add it to your data file.
751. Unit size
RS April 28th, 2009, 7:01am:
Dear Mike
I have two Mathematics tests (Grade 7 and Grade 9) which are linked by 16 common items. When I assessed the quality of the vertically linked items I realised that three of them did not functioned as link. As a result, these items were dropped from the link and treated as unique items.
Further investigation reveals that the standard deviation of common items are different (SD for Grade 7 and Grade 9 is 1.75 and 1.97, respectively) indicating that common items in Grade 9 are more discriminating. Different variances also indicate that two scales are different in terms of unit size.
My questions are:
1. What will be happened if I use the concurrent equating procedure (adjust for both origin and unit size) to place all the items on a common scale?
2. Am I ignoring the differences in the unit size if I use translation constant to shift two scales on a common scale?
Regards
RS
MikeLinacre:
Thank you for your questions, RS.
You have identified some of the challenges in vertical equating.
Here is a suggestion.
Reanalyze your data, trimming off responses to items which are too easy and too hard for each child. In Winsteps, CUTLO= and CUTHI=.
Does this bring the common item S.D.s closer together?
A. If so, then it is off-dimensional behavior on very easy and very hard items (for the child) which is distorting the measures. Do the item analysis and equating with the trimmed data. Anchor the items. Then produce the final person measures with all the data.
B. If not, then the nature of the latent variable is changing. We can see this in language tests as the latent variable changes from "learning vocabulary and rules of grammar" (recall: lower-order mental skill) to "understanding and composing text" (higher-order skill).
There are several decisions here:
a. Which vertical level is the benchmark level? If one level is more important, equate to it.
b. If levels are equally important, then Fahrenheit-Celsius equating may be required.
To answer your questions:
1. What will happen? There will be some misalignment of children and items with measures far away from the mean of the common items. From your numbers, we can see that the misalignment will be about 0.25 logits for a child or item about 2 logits from the mean of the common items. If the usual rule that "one grade level = one logit" applies in your case, then that discrepancy will have no practical effect on placement decisions, etc.
2. Yes, you are ignoring differences in unit size. But here the difference is practically small.
RS:
Thanks a lot, Mike. THe SDs of trimmed data are now very close.
RS:
Dear Mike
I would appreciate your comments on the following issue.
In this example, imagine that the SDs of trimmed data for Year 7 and Year 9 is 1.75 and 1.95 respectively, and both levels are equally important. For your information, the translation constant to shift these two year levels onto a common scale is 1.05 logits. You mentioned that a Fahrenheit-Celsius equating is required.
Does it mean I need to use the following formula and adjust for both origin and unit size?
(�7*1.75/1.95) + 1.05) = �7 on 9
Regards
RS
MikeLinacre:
Thank you, RS.
If year 7 common items have mean=M7 and SD=SD7
and year 9 common items have mean=M9 and SD=SD9
then to transform a year 7 measure X7 into year 9 measure X9,
(X7-M7)*SD9/SD7 + M9 = X9
752. Rasch model & live testing program
RS May 29th, 2009, 6:33am:
Hello every one
Eight Mathematics Tests (Year 3 to Year 10) are given to about 15,000 students from 10 different countries. The sample size for each year level is at least 1000 (more than 100 students from each country). I have been asked to apply Rasch measurement model to analyse data from a large scale testing program and report the results in two levels 1) for each country separately and, 2) for all countries together. The initial analyses indicate that there are plenty of misfitting items, misfitting persons and items with large gender and country DIF. This is a live testing situation so I am not supposed to remove any items, or persons.
Would some one would throw some lights and tell me what is the best way to deal with this situation. Should I delete those students with strange response pattern to bring my data to fit the model for the purpose of scale construction and added them to the data set for measurement purpose? Should I calibration all items simultaneously or should I do analysis by year level and country?
Many thanks and regards
RS
MikeLinacre:
Thank you for your questions, RS.
Person misfit has to be huge, and affect a large proportion of the sample, for it to alter the measures noticeably, but this could apply if your samples are "low stakes", so that they have little motivation to "behave" as they respond to the tests. You could remove misfitting persons, calibrate and anchor the items, and then reinstate those persons for the final reporting.
TIMSS 2007 http://timss.bc.edu/TIMSS2007/PDF/T07_TR_Chapter11.pdf apparently made no adjustment for DIF (gender or national).
Adjusting for gender DIF will probably be too confusing and controversial, but it may be useful to report for each country, but the sample sizes may be too small for a gender-dif study by country.
Country DIF is probably a reflection of the different curricula in the different countries. This is a policy decision. Which curriculum has pre-eminence? You may want to use the standard curriculum for "all countries together", then anchor all items, except for items DIFed for that country, for each country's analysis.
Ray Adams at ACER may have a technical paper which discusses this.
RS:
Thanks a lot Mike.
One more issue. In this study, common items were used to link these eight Mathematics Tests and to construct a Mathematics scale. Separate and concurrent equating procedures are two widely used equating methods. When data fit the Rasch model well enough, the results emerged from these two equating procedures are expected to be comparable. However, the equating results produced by these two procedures are expected to become less comparable as model-data fit gets progressively worse. In other words, these two procedures generate different results as model-data fit deteriorates.
Considering the significant amount of misfit in my data, which equating procedure would do the job better? While some test practitioners go with the procedure that gives the best results I am interested to know which procedure produces the most legitimate and defensible results?
Many thanks.
RS
MikeLinacre:
Concurrent vs. Separate equating, RS?<br>
We debated this in 1988 https://www.rasch.org/rmt/rmt22.htm.<br>
In summary, separate equating is always safer, because it allows detailed quality control of every link. But separate equaing is also much more awkward to implement and considerably more error prone.<br>
So, if the cross-plots of the the common items for pairs of forms, produced during separate equating, indicate that a concurrent equating will work (usually with some "common" items coded as unique items for some forms), then concurrent equating is preferable.<br>
Other advantages of concurrent equating are that we don't specify which form(s) set the standard and we avoid many of the arbitrary decisions which must be made about each link. This arbitrariness accumulates down the linked-chain of tests.
RS:
Thanks a lot Mike. I found those sources very useful.
Regards,
RS
753. WINSTEPS' Vs. FACETS' rating scale tables
siyyari June 3rd, 2009, 4:09pm:
Hi Dr. Linacre
Thanks for your comprehensive reply to my previous questions. They were most useful. Now I have some other questions, I hope they are not very off the track.
In order to carry out partial credit analysis on my writing rating scale, I have used both WINSTEPS and FACETS. My scale consists of 5 components (items) originally scored on a Likert scale. By using WINSTEPS, when I request rating (partial credit) scale output tables, one separate table of fit statistics and structure calibrations is provided for each component of the scale. However, when I use FACETS, one general table of Category Statistics, containing fit statistics and RASCH-ANDRICH THRESHOLDS, appears taking all the components together, i.e. only one set of calibrations is provided for all the items or components.
1) Do these two tables from the two softwares contain the same information?
2) Are RASCH-ANDRICH THRESHOLDS for all the components together produced by FACETS the same as Structure Calibrations produced by WINSTEPS?
3) Are the Category Measures produced by WINSTEPS the same as Expectation Measure at Category produced by FACETS?
4) I would like to rescale the logit values to a scale ranging from 1 to 20. I think a linear transformation by forming a linear equation as explained in the FACETS manual will do the job. Now I wonder if I should use the RASCH-ANDRICH THRESHOLDS (in FACETS) or the Expectation Measure at Category values for the rescaling. My own guess is Expectation Measure at Category since RASCH-ANDRICH THRESHOLDS are provided for category score 2 to 5, nothing is mentioned for category score 1 but Expectation Measures at Category are given for all the category scores which makes the rescaling possible. the same is true about about WINSTEPS table in which Category Measures cover all the category scores but Structure Calibrations start from category score 2 to 5, but not 1.
As usual, my thanks in advance for the time and attention and my apologies for my complicated and amateur-like questions.
MikeLinacre:
Thank you for your questions, Siyyari.
1) For the Partial Credit model (Groups=0 in Winsteps, "#" in Facets), there is a separate table of category information for each items (Table 3.? in Winsteps, Table 8.? in Facets).
2) Yes. Structure Calibrations = Rasch-Andrich thresholds
3) Thank you for asking this. I had not thought to parallel the outputs.
Winsteps Table 3.2 field = Facets Table 8 field
CATEGORY LABEL = Category Score
CATEGORY SCORE = Category Score
COUNT = Used
% = %
... = Cum. %
OBSVD AVRGE = Avge Meas
SAMPLE EXPECT = Exp. Meas
INFIT MNSQ = ...
OUTFIT MNSQ = OUTFIT MnSq
STRUCTURE CALIBRATN = RASCH-ANDRICH Thresholds Measure
*CATEGORY MEASURE = EXPECTATION Measure at Category
*STRUCTURE MEASURE = RASCH-ANDRICH Thresholds Measure
STRUCTURE S.E. = RASCH-ANDRICH Thresholds S.E.
*SCORE-TO-MEASURE AT CAT. = EXPECTATION Measure at Category
*SCORE-TO-MEASURE --ZONE-- = EXPECTATION Measure at -0.5
*50% CUM. PROBALTY = RASCH-THURSTONE Thresholds
COHERENCE M->C = ...
COHERENCE C->M = ...
ESTIM DISCR = ...
... = MOST PROBABLE from
... = Cat PEAK Prob
OBSERVED-EXPECTED RESIDUAL DIFFERENCE = Obsd-Expd Diagnostic Residual
(text to right of table) = Response Category Name
* = In Winsteps only, includes item difficulty for Partial Credit model
4a) Rescaling: Usually I look at the logit range in Table 6, and transform that range. For instance, if Table 6 shows -6 logits to +4 logits, and the rescaled values are to be 1 to 20, then
-6 => 1
4 => 20
so that the multiplier (uscale) = (20- 1)/(4 - -6) = 19/10 = 1.9
and the new "zero" point (umean) = 1 - (-6 * 1.9) = 12.4
Umean = 12.4, 1.9
To verify:
-6 will be 12.4 + 1.9 * -6 = 1
4 will be 12.4 + 1.9 * 4 = 20
4b) Rasch-Andrich thresholds are points of equal probability between adjacent categories, so there is always one less threshold than category.
754. How to classify rasch within the sciences
ayadsat June 2nd, 2009, 6:50am:
I have used Polytomouse item response theory to estimate examinee's ability. Can I consider the ability estimation algorithm is the same machine learning (as in computer science)?
Can I classify rasch theory or item response theory within the field of artificial intelligence?
Thank you very much :)
MikeLinacre:
Thank you for your questions, Ayadsat.
The use of Rasch models within computer-adaptive testing supports learning about the ability of the person.
Rasch models are mathematical transformations of probabilistic ordinal observations into additive measures. Rasch models also support statistical analysis of the extent to which the data conform with the requirements of the transformation.
Item Response Theory (as defined by its originator, Frederic Lord) is a descriptive statistical technique, and so is classified with regression analysis, factor analysis, etc. The Rasch model can also be used as a descriptive technique.
OK?
ayadsat:
Thank u very much for this valuable information
755. heterogeneous sample
siyyari June 1st, 2009, 4:24pm:
Hi Dr. Linacre
I am conducting Rasch Partial Credit Model to determine the scalability and interval distances between the score categories on a writing rating scale. my questions now are as follows:
1. Does choosing a heterogeneous sample help to have a smaller sample (as small as 30)? if yes, is it acceptable among all Rasch scholars?
2. If my sample is small (30), and the fit statistics are all within acceptable range, can i claim that my data is unidimensional and the sample size is enough?
3. After obtaining the step calibrations (RASCH-ANDRICH THRESHOLDS), how can I apply the same distances on my original likert scale? Please provide me with a straightforward solution.
If you can also introduce me a comprehensive reference in this regard, I do appreciate it.
Thanks in advance
MikeLinacre:
Thank you for your questions, Siyyari.
1. Heterogeneous sample:
We usually want a sample that corresponds to the population for which the writing instrument is intended, and with an ability range that also corresponds the intended range.
If your target population has two types of persons (for instance, native speakers and second-language speakers), then you must decided which type are definitive, and select your sample accordingly.
2. Sample size, fit and unidimensionality.
If your fit statistics are local (such as Infit and Outfit) then they are insensitive to dimensionality. Please use a different technique, such as principal components analysis of residuals to investigate dimensionality.
Fit tests are also insensitive with small sample sizes.
A sample size of 30 is usually sufficient to verify the construct validity and predictive validity of an instrument for practical use, but it is not sufficient for convincing fit or dimensionality analysis. In the same way, a piece of knotted string is good enough for measuring a garden, but not good enough for carpentry.
3. Applying thresholds
The Rasch-Andrich thresholds specify the interval on the latent variable in which a category is the most likely one to be observed. We can draw a picture of this for each item and match it to each person in the sample. For instance, Winsteps Table 2.1 www.winsteps.com/winman/table2.htm
4. Reference: "Applying the Rasch Model" (Bond & Fox) is a good place to start.
756. person misfit
flowann May 14th, 2009, 2:04pm:
hi everyone,
we investigated the Rasch model on a questionnaire about perceived participation of 286 persons. Of course, we wanted to study the internal scale validity of the questionnaire. We had a high rate of 15,7% of respondents who were underfitting. Almost the same high underfit happens in a different population, but mostly, the person response validity is not mentioned in publications.
We did not find any underlying patterns to explain the misfit.
Our question:
How meaningful is person response validity to be discussed and investigated in depth?
Are there any experiences out there?
Thank you!
flowann
MikeLinacre:
Thank you for your questions, Flowann.
How are you defining "underfit"?
https://www.rasch.org/rmt/rmt83b.htm suggests the mean-square range 0.6 - 1.4.
What range are you using?
flowann:
hello Mike,
underfit = infit Z> 2, and infit MnSq > 1,4.
flowann
MikeLinacre:
Flowann, thank you for those criteria.
They are "underfit = infit Z> 2, and infit MnSq > 1,4."
That sounds reasonable, please make sure that you are not using:
"underfit = infit Z> 2, or infit MnSq > 1,4."
We need misfit to be both statistically unexpected and substantively large.
Please analyze only that 15.7% of respondents who misfit. Does their analysis produce a different item-difficulty hierarchy than the complete analysis?
If it does not, then the misfitting respondents are not threatening the validity of the complete analysis, and so may be kept in that analysis.
If it does, then the difference in item hierarchy provides useful information about how the misfitting persons differ from the majority of the persons.
flowann:
Hello Mike,
First of all, thanks a lot for the answer of my/our question on the forum. Me and my colleague in research went further with
this information and, as often happens, we encountered more questions.
We hope we get answers on those too!
1. If Rasch analysis of only the "misfitting" respondents reveals no difference in item
hierarchy, what does that mean? Is the high misfit rate among
respondents then no harm to the validity of the questionnaire? If that
is the case, why not?
2. Is there in that case no reason to report these results on person
response validity in an article? In other words: Could a good outcome
of this kind of secondary analysis on misfitting respondents be the
reason that most authors (of articles with Rasch analysis involved)
don't report person response validity at all? In our opinion, it would
be good for the reader to know that person response validity has been
taken into consideration.
3. In our case, the Rasch analysis with the misfitting respondents
resulted in a very different item hierarchy. What does this mean
exactly? Is the 15.7% than even more a threat to the construct
validity than it already was?
4. What should be said about construct validity then, taken in
consideration that item response validity was very good (only one
item, less than 5% was misfitting and after deletion of this item no
item misfitted in the next Rasch analysis)?
5. Where can we find references/literature about those issues?
Hope to get some answers!
Greetings,
flowann
MikeLinacre:
Thank you for your questions, flowann.
1. "Misfitting" and the item hierarchy.
A well known-form of misfit is "random guessing". This does not change the item hierarchy, but it does lessen the validity of the person measures. To obtain a more accurate picture of the item hierarchy, omit the guessers (or their guesses) from the data. Analyze the items. Then anchor (fix) the item-difficulty measures, and reanalyze everyone.
2. Person validity. In classical test theory (CTT) and most item response theory (IRT), no individual person fit-statistics are computed, and often only a summary "test" reliability is reported. Rasch is unusual in its concern about person fit. So, I agree with you about person validity.
3. "a very different item hierarchy"
This is a serious threat to the construct validity of the instrument. What do you intend to measure? Which hierarchy accords with your intention? This is like the early thermometers. They measured temperature, but were also heavily influenced by atmospheric pressure. So the scientists at that time had to disentangle these two different variables. Focus on what you intend to measure. Select the data that corresponds to that intention. And then analyze it.
4. "item fit"
Consider the "random guessing" situation. If that was evenly spread among the items, then all the items would fit the Rasch model equally well. No problems would be reported for the items. But for the persons, the randomness would be uneven. The guessers would have a different, accidental, item hierarchy. The non-guessers would show the reported item hierarchy, but even more strongly.
5. References/literature:
This is mentioned in "Applying the Rasch Model" (Bond & Fox), but psychometric research has focused much more on the items than the persons. And, of course, there is Google .... :-)
757. DIF
RS May 26th, 2009, 10:00am:
Hi Mike
A Mathematics test with 45 items is given to 3000 Year 5 students from five different states. I am interested in assessing the state DIF. I have used RUMM software for this purpose. The results of my analysis indicate that there are nine items displaying state DIF (p<.001). There is no systematic DIF in favor of one particular state. But, the magnitude of DIF is not equal for all those nine items. For example, some time the ICCs for different states are very close but still statistically significant. In the other cases, however, the ICCs are fall apart extremely.
I wonder if there is a way to quantify the DIF for each item and then take the average and make decision about the total DIF in the test.
MikeLinacre:
RS, thank you for your questions.
There are several ways to quantify the DIF for each item. In RUMM, one approach would be to split a suspect item by state. You would then get 5 difficulties for the item, one for each state.
With your large sample size, you are likely to find statistically-significant DIF with no substantive impact. The ETS criteria for substantive impact are shown at www.rasch.org/rmt/rmt32a.htm and many other webpages.
connert:
Hi RS,
One part of your problem is analogous to doing pairwise t-tests rather than ANOVA. You need to control for the likelihood of getting significant differences simply because of the number of comparisons you are considering. The results you are reporting could be simply random variation that is expected because of the number of items and the sample size. I am not aware of a correction factor for your situation but you do need to beware of attributing substantive importance to DIF results that may be within expected variation.
Tom
RS:
Dear Mike and Tom
Thanks a lot for your inputs.
Regards
RS
758. Category Scale Curves (suite)
bahrouni May 23rd, 2009, 6:48am:
Hi Mike,
Sorry, here's the 2nd attachment. I had difficulties in attaching both of them together in the same posting.
I am using MFRM to analyze the analytic rating of 3 EFL essays by 56 raters. I'd like to look at the impact of the raters' backgrounds on their way of rating. I have divided the raters into three groups as you suggested in an earlier posting: 1) native speakers, 2) Arabic speakers (who share the students' L1 + culture) and 3) other: non-native & non-Arabic speakers.
The essays are assessed on 4 categories: Task achievement, Coherence & Cohesion, Voc. and Gr. using a 25-point scale to get the total raw score out of 100 (4x25).
The problem I have faced is that on entering the raw scores (rounded up: no decimals) as they are out of 25, I had messy scale curves; I mean those hills for the different scores have no separate peaks. Add to this, the numerical values are different from the ones entered. Please see the attachement (25-pnt scale) to have a clearer idea of what I am talikng about.
Earlier in a pilot analysis, I had the same problem. Professor James Dean Brown, who had introduced me to MFRM, was around for our conference, so I had a chance to show him the results from my pilot analysis and asked him about that problem. He suggested that I should make the scale smaller. So I divided the scales by 5 so as to have a 5-point scale for each of the categories. It worked well.
When I tried the same thing this time, it has also worked well but I have noticed the following:
1) the vertical ruler is much longer than the 25-point scale.
2) the measures are not the same: the logit scale does not show the same measures for the most severe/lenient raters; the most/least able students; the most difficult/easiest category.
Please see the attachment (5-pnt scale) to compare it to the 25-pnt one.
I have also noticed that when dividing the initial raw scores (out of 25) by 5 and round them up, it takes 2.5 points to move from K-1 to k up the scale. For example all the raw scores between 7.5 and 12.49 out of 25 are equal to 2 out of 5; those between 12.5 and 17.49 out 25 are 3 out of 5, etc.. This has made feel that this dividing issue is making the analysis less sentive to differences between the abilities.
Is there another way of doing it?
Thanks a lot for your help
Bahrouni
759. Center item mean = 0 and anchor person ability
ong May 17th, 2009, 2:55pm:
Hi,
I would like to calibrate a dataset (2982 persons and 52 dichotomous items) and center the mean of item difficulty to 0. Person ability measure is anchored from another calibration.
&INST
TITLE = "Calibration with anchor person ability"
PERSON = Person ; persons are ...
ITEM = Item ; items are ...
ITEM1 = 6 ; column of response to first item in data record
NI = 52 ; number of items
NAME1 = 1 ; column of first character of person identifying label
NAMELEN = 5 ; length of person label
XWIDE = 1 ; number of columns per item response
CODES = 01 ; valid codes in data file
UIMEAN = 0 ; item mean for local origin
USCALE = 1 ; user scaling for logits
UDECIM = 2 ; reported decimal places for user scaling
PAFile =Pfile1.txt;
SAFile =Sfile.txt;
&END
However, the output results the mean is 0.77 and not 0.
I am using Winsteps 3.68.1.
What did I miss out in the command?
What should I do to make sure that the item difficulty mean is centered at zero?
SUMMARY OF 52 MEASURED (NON-EXTREME) Items
-------------------------------------------------------------------------------
| RAW MODEL INFIT OUTFIT |
| SCORE COUNT MEASURE ERROR MNSQ ZSTD MNSQ ZSTD |
|-----------------------------------------------------------------------------|
| MEAN 1992.2 2892.0 .77 .06 1.07 2.3 1.17 2.1 |
| S.D. 505.1 .3 1.39 .01 .15 4.9 .36 4.5 |
| MAX. 2802.0 2892.0 3.45 .12 1.43 9.9 2.40 9.9 |
| MIN. 850.0 2891.0 -2.55 .05 .81 -8.0 .58 -6.2 |
|-----------------------------------------------------------------------------|
| REAL RMSE .06 ADJ.SD 1.39 SEPARATION 23.14 Item RELIABILITY 1.00 |
|MODEL RMSE .06 ADJ.SD 1.39 SEPARATION 24.13 Item RELIABILITY 1.00 |
| S.E. OF Item MEAN = .19 |
-------------------------------------------------------------------------------
Ong
MikeLinacre:
Thank you for your questions, Ong.
The person-measure anchor values, combined with the data, determine the zero on the measurement scale. So the UIMEAN=0 instruction is ignored.
If you want the mean item difficulty to be zero, then please subtract .77 from all the person anchor values.
760. changing 50% threshold (limen?)
franz May 4th, 2009, 12:19pm:
Hi, I am new to Rasch analysis (I'm now reading Bond&Fox).
I would like to obtain a personal score for my students on a group of test items from the PISA survey, by using the same "rules" as in PISA.
In PISA a score of, say, 438 means that you have 62% odds (and not 50% as it is default in Winsteps/Ministep!) of answering correctly to an item rated 438. How can I set this threshold from 50% to 62%?
Thank you for helping a newbie ;-)
franz
MikeLinacre:
Thank you for your question, Franz.
The default for item difficulties and person abilities is 50% success.
You want to adjust that to 62% success.
In your control file, include:
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
When you look at Table 1, you should see that the person abilities are now lower relative to the item difficulties.
franz:
Thank you very much for your answer, Mike.
It saves my day.
I would ask a second question: some of my test items are polytomous (scoring can be 0/1/2/3). Is it enough to include in the control file the lines
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
or shall I add 2 more lines with walues corresponding to 2 and 3 points?
I am afraid this question reveals my poor understanding of the math underlying Rasch: I apologize.
Thanks again
franz
MikeLinacre:
Franz, polytomies are much more difficult.
Does "62%" mean "62% of the maximum score" = .62*3 = 1.86?
If so, we need to make a logit adjustment to all the category thresholds equivalent to a change of difficulty corresponding to a change in rating of .62*3 = 1.86.
This is intricate:
1. We need the current set of Rasch-Andrich thresholds (step calibrations) = F1, F2, F3.
2. We need to compute the measure (M) corresponding to a score of 1.86 on the rating scale
4. Then we need to anchor the rating scale at:
SAFILE=*
0 0
1 F1 - M
2 F2 - M
3 F3 - M
*
An easy way to obtain M is to produce Winsteps "Output Files" menu, GRFILE= and then look up the Measure for the Score you want.
franz:
Dear Mike,
sorry for the late reply, I am sort of struggling with the software.
I am still working on dicothomous items.
I made an item anchor file with the following values taken from OECD-PISA documentation:
1 478 ; item 1 anchored at 478 units
2 540 ; item 2 anchored at 540 units
3 600 ; item 3 anchored at 600 units
4 397 ; item 4 anchored at 397 units
5 508 ; item 5 anchored at 508 units
I analyzed the file and I think I got reasonable results (with person measure meaning a 50% odds of getting right a test item at that measure).
To have a measure corresponding to 62% odds I then followed your indications and added these lines to the control file:
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
but they seem not to make a difference in the person measure (output table 17). I do not get a lower score, as expected.
I tried replacing the line
1 -0.489548225 ; ln(38%/62%)
with other values after 1, but this does not seem to affect the person measure. Am I missing something?
A second question regarding politomous items
The OECD PISA provides a table with the difficulty associated with each level of response to politomous items. Is it wrong to recode a polytomous item with, say, 2 levels of correct answers (1/2), into 2 dicotomous items? The raw score would not change, but would it affect person measure? It does seem easier to work with dicotomous items.
Thank you again for your patience
Franz
MikeLinacre:
Franz:
Your question 1) Here is an experiment with Winsteps Example file: Exam1.txt
a) Add these lines to it:
UIMEAN=500
USCALE=100
then Table 18:
--------------------------------------
|ENTRY TOTAL MODEL|
|NUMBER SCORE COUNT MEASURE S.E. |
|------------------------------------+
| 1 7 18 205.72 82.41|
b) Also add:
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
--------------------------------------
|ENTRY TOTAL MODEL|
|NUMBER SCORE COUNT MEASURE S.E. |
|------------------------------------+
| 1 7 18 155.11 82.47|
If you are using UPMEAN=500, then the person measures do not change, but the item measures do change.
Your question 2) "it wrong to recode a polytomous item with, say, 2 levels of correct answers (1/2), into 2 dichotomous items?"
This was a method we used before polytomous software became widely available. The measures from the recoded data are usually more diverse than from the original data, so you will need to do a "Fahrenheit-Celsius" conversion on the measures on the recoded data to return them to approximately the same measurement scale as the original data.
franz:
Dear Mike,
I must be making some stupid error, but I cannot replicate your experiment with Winsteps Example file: Exam1.txt
I do get your table 18 with
--------------------------------------
|ENTRY TOTAL MODEL|
|NUMBER SCORE COUNT MEASURE S.E. |
|------------------------------------+
| 1 7 18 205.72 82.41|
but when I add:
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
I get
--------------------------------------
|ENTRY TOTAL MODEL|
|NUMBER SCORE COUNT MEASURE S.E. |
|------------------------------------+
| 1 4 14 205.24 82.41|
with a measure which is only .48 lower than the previous one.
I am sorry for abusing your patience, but do you have any idea of what am I doing wrong? Thanks
Franz
MikeLinacre:
Franz, this is mysterious. The raw scores have changed!
Please try two analyses of Exam1. txt
One with these lines added. Please add them at the top of Exam1.txt, and remove any other SAFILE= lines.
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 0
*
And one without those lines (no SAFILE=).
The results of the two analyses should be the same.
franz:
Thanks Mike,
when I follow your last suggestion I do get the same analysis, and I also get lower person measure if I set the the 62% threshold with
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
The problem is that I get (nearly) the same person measure with files beginning with the following lines:
case 1:
UIMEAN=500
USCALE=100
case 2:
UIMEAN=500
USCALE=100
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 0
*
case 3:
UIMEAN=500
USCALE=100
UASCALE=1 ; anchoring is in logits
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
It seems that UIMEAN USCALE or UASCALE override the SAFILE= anchor
I also get the same results if I put the lines
SAFILE=* ; anchors the response structure
0 0
1 -0.489548225 ; ln(38%/62%)
*
after a IAFILE= command which anchors each item at its PISA difficulty.
I really appreciate your patience, but please feel free to tell me that me or my case are hopeless ;-)
Franz
MikeLinacre:
Thank you, Franz.
The order of the instructions in the Winsteps control file does not matter, except that only the last instruction of any one type is performed. So if you have SAFILE= in the control instructions twice, only the last SAFILE= is actioned.
What version of Winsteps are you using? There have been some changes in the anchoring instructions between versions.
Attached is the Winsteps control file that works for me. Adam's measure is 155 with SAFILE= anchoring, and 205 without.
761. choosing a rating scale vs.partial credit model
pjiman1 May 12th, 2009, 6:35pm:
Choosing a rating scale vs a partial credit model
Hi Mike,
Thanks for your help in the past.
I wish to know your opinion about choosing a rating scale vs a partial credit model for analysis.
I have 16 items, 4 rating categories. The rating categories are 1 = no development, 2 = limited development, 3 = mostly functional level of development, 4 = fully functional development. Each of these rating categories has separate criteria that were developed for each item in order to make the rating. I have three waves of data.
My task is to see if the scale and its dimensions are invariant over time. But first, I need to determine which RASCH model to use - rating scale or partial credit.
Choosing a rating scale is appealing because of its ease of interpretation and scoring. The drawback is that it might not be precise.
Choosing a partial credit model is appealing because it is more precise because it allows for the fact that for some items, different rating category systems should be used. The drawback is that it is more complicated to interpret and score.
Andrich (1979), I believe would say that for most psychological constructs, a rating scale model works because participants use the rating scale consistently across all the items. Partial credit model is used because across all items (say a math aptitude test), some answers deserve partial credit, some deserve full, and some get no credit. This allows for more precision in predicting person and item difficulty.
My goal is to determine which model is better for analyzing these items, with a desire to see that these items remain invariant on their dimensions across waves.
I am using AIC (Akaike's information criterion) to compare the models. The model with the lower AIC score indicates which one is better.
 
Here are my results:
Step 1 - wave 1, all items,
Rating scale model: LOG-LIKELIHOOD CHI-SQUARE: 1613.13
82 PERSONS 16 ITEMS MEASURED: 81 PERSONS 16 ITEMS 4 CATS
3 steps + 82 = 85 * 2 = 170, 170 + 1613.13 = 1783.13
Partial credit model: LOG-LIKELIHOOD CHI-SQUARE: 1503.03
82 PERSONS 16 ITEMS MEASURED: 81 PERSONS 16 ITEMS 64 CATS
82 + 48 = 130 * 2 = 260, 260 + 1503.03 = 1763.03
Higher AIC loses - Rating scale AIC = 1783.13 > Partial Credit AIC = 1763.03
At wave 1. Partial Credit wins, but not by much.
Rating scale model: LOG-LIKELIHOOD CHI-SQUARE: 1985.10 with 1054 d.f. p=.0000
79 PERSONS 16 ITEMS MEASURED: 75 PERSONS 16 ITEMS 4 CATS
3 steps + 79 = 82 * 2 = 164, 164 + 1985.10 = 2049.10
Partial credit model: LOG-LIKELIHOOD CHI-SQUARE: 1891.19
INPUT: 79 PERSONS 16 ITEMS MEASURED: 75 PERSONS 16 ITEMS 63 CATS
79 +48 = 125 * 2 = 250, 250 + 1891.19 = 2141.19
Higher AIC loses - Rating scale AIC - 2049.10 < Partial Credit AIC = 2141.19
At wave 2, Rating scale wins
Rating scale: LOG-LIKELIHOOD CHI-SQUARE: 1716.60
65 PERSONS 16 ITEMS MEASURED: 62 PERSONS 16 ITEMS 4 CATS
3 steps + 65 persons = 68 * 2 = 136, 136 + 1716.60 = 1852.60
Partial credit model: LOG-LIKELIHOOD CHI-SQUARE: 1591.75
65 PERSONS 16 ITEMS MEASURED: 62 PERSONS 16 ITEMS 62 CATS
65 + 48 = 113 * 2 = 226, 226 + 1591.75 = 1817.75
Higher AIC loses - Rating Scale AIC = 1852.60 > partial credit model AIC = 1817.75
Partial credit model wins
My conclusion is that the partial credit model wins because two out the three waves favor partial credit based on the AIC test (although the AIC values do not differ too much, less than 100 pt difference). Also, the rating scale does not have the same criteria for each item; there are different criteria for each item for raters to make a decision on how to rate the item. However, based on the rating scale categories, it does seem that overall, respondents are using each of the rating scale categories. So, I seem to have a toss-up. On the one hand, it would seem that rating scale would be supported by the rating scale category outputs, plus I do desire to have a simpler model and the rating scale model would do that. However, a comparison of the models does suggest that the partial credit model works better, and when I look at the rating scales for each of the items, there are a few items with disordered categories. So I�m leaning towards the partial credit model. Do you concur with my conclusion? Or am I off base?
Summary tables and rating scales tables for each wave are in the attached word file.
Many Thanks in advance.
Pjiman1
MikeLinacre:
Thank you for telling us about your analysis, Pjiman1.
PCM vs. RSM is a difficult decision. Here are some considerations:
1. Design of the items.
If the items are obviously intended to share the same rating scale (e.g., Likert agreement) then the Rating Scale Model (RSM) is indicated, and it requires strong evidence for us to use a Partial Credit Model (PCM).
But if each item is designed to have a different rating scale, then PCM (or grouped-items) is indicated, and it requires strong evidence for us to use RSM.
2. Communication with the audience.
It is difficult to communicate many small variants of the functioning of the same substantive rating scale (e.g., a Likert scale). So the differences between items must be big enough to merit all the extra effort.
Sometimes this difference requires recoding of the rating scale for some items. A typical situation is where the item does not match the response-options, such as when a Yes/No item "Are you a smoker?" has a Likert-scale responses: "SD, D, N, A, SA".
3. Size of the dataset.
If there are less than 10 observations in a category used for estimation, then the estimation is not robust against accidents in the data. In your data set, RSM does not have this problem. But 4 categories and 62 measured persons indicate that some items may have less than 10 observations in some categories. This may be evidence against PCM.
4. Construct and Predictive Validity.
Compare the two sets of item difficulties, and also the two sets of person abilities.
Is there any meaningful difference? If not, use RSM.
If there is a meaningful difference, which analysis is more meaningful?
For instance, PCM of the "Liking for Science" data loses its meaning because not all categories are observed for all items. This invalidates the item difficulty hierarchy for PCM.
5. Fit considerations.
AIC is a global fit indicator, which is good. But global-fit also means that an increase in noise in one part of the data can be masked by an increase in dependency in another part of the data. In Rasch analysis, underfit (excess non-modeled noise) is a much greater threat to the validity of the measures than overfit (over-predictability, dependency). So we need to monitor parameter-level fit statistics along with global fit statistics.
Hope some of this helps you, Pjiman1.
762. Rasch Core Topics - Online Course 26th June
Sue_Wiggins May 11th, 2009, 10:31am:
Hi
I am thinking of undertaking the Rasch online course 'Practical Rasch Measurement - Core Topics'
by Dr. J. Michael Linacre 26th June. I have a good grounding of Stats but my concern is that the course requires 'the ability to manipulate an Excel spreadsheet'. Can anyone tell me to what extent the course requires to students to be able to manipulate Excel. I can do basic stuff like summing coloumns or finding the mean of columns but wouldn't know how to get it to do complex formula.
Any help appreciated.
Sue
MikeLinacre:
Thank your for your interest in the Course, Sue.
Yes, you can "manipulate an Excel spreadsheet"!
The "Rasch - Core Topics" Course is not a Course in Excel, so all Excel operations have precise step-by-step instructions.
Of course, if you want to do more with Excel, you can!
Forum members: Any comments about this from any of the 308 participants in that Course across the years?
Sue_Wiggins:
Thanks for that Mike. Think I will enrol.
Sue
763. Trouble with MFORMS CTL FILE
ImogeneR May 12th, 2009, 5:18am:
Hi,
I've been trying to create my own concurrent analysis (for common items across 2 test sittings of similar tests). I think I am almost there with MFORMS but looking at the 'edit mforms' I know my data isn't lining up. ..it seems to be something to do with the P= person label command..any help would be MUCH appreciated. I have attached my control file and the "edit mforms output" and one of the data file. (Common items are all in first 38 item columns and in same column position..).
Thanks Imogene.
Actually it won't let me add the datafile structure but it was simply 9 digit IDnumber (columns 1-9) then the item responses, the first 38 items in both data files are the common ones..
MikeLinacre:
This should solve it, Imogene.
MFORMS=* ; analyze multiple data files with different item columns
data= "1 RFA 1 2008 V2.TXT" ; the 2008.txt data file
L=1 ; one line of input data per data record
P1-9=1
I1-38=10 ; item in combined file = column in original data file
I39-119 = 48
#
data="1 RFA 1 2009 V2.TXT"
L=1 ; one line of input data per data record
P1-9=1
I1-38=10
I120-201=48
*
764. stats reports
ImogeneR April 23rd, 2009, 2:07am:
Hi
Just wondering if there is anyway I could get stats out of Winsteps in an output file that would show the following per line of data (item) from analysis :
item measure, infit, point biserial and % (of cohort) selected for each distractor in a 1 from 5 SBA?
Is there any way to program this? I have to export 2 different files at the moment and clean out some unwanted columns before I can import into an exam database...
I realise it might be wishful thinking!
Thanks
MikeLinacre:
Sorry, no, ImogeneR.
It looks like DISFILE= and IFILE= are the best we can do.
Writing them both as Excel files may ease the data formatting.
This does suggest that a report-writer add-on to Winsteps would be useful.
ImogeneR:
Thanks Mike,
And it would be nice to have a build your own query report writer or export - sort of like the way spss lets you choose fields for an analysis..or like an access query..
Cheers
Imogene
MikeLinacre:
You are so right, Imogene. That would be nice!
765. subtest analysis
omardelariva May 9th, 2009, 12:31am:
Hi everybody:
I want to calibrate a test that includes ten subtests in only one data file. Each subtest measures different latent trait (mathematics, spanish, phisics, biology, etc.). I do not want make a control file and a data file for each subtest, so I used MFORMS command then I could solve the problem but I have to run WINSTES ten times and change MFORMS command. I would like to use only one control file, one data file, to run one time WINSTEPS and do not mix latent traits. Is it possible?
Thank you for your help.
MikeLinacre:
Thank you for your question, Omardelariva.
You will need to run 10 analyses, one for each latent trait.
But you only need one control file and one MFORMS= command.
Code each item with its subtest as the first letter of the item label.
Then you can use ISELECT=(letter) to select the subtest you want.
You can type ISELECT=(letter) at the Winsteps "Extra Specification?" prompt.
OK?
If you are familiar with "batch" commands, then you can set up one batch file to do all 10 analyses:
analysis.bat is a text file in the same folder as your control file:
START /w c:\winsteps\winsteps.exe batch=yes controlfile.txt outputA.txt ISELECT=A
START /w c:\winsteps\winsteps.exe batch=yes controlfile.txt outputB.txt ISELECT=B
....
START /w c:\winsteps\winsteps.exe batch=yes controlfile.txt outputJ.txt ISELECT=J
In that folder, double-click on analysis.bat to run the analyses.
766. Fit and bias analysis in Facets
bahrouni May 4th, 2009, 5:54am:
Hi Professor Linacre,
I am analyzing the rating of 3 EFL student essays marked by 50 teachers on 4 categories using a 5-point scale. I am using a 4-facet model: examinees, raters, categories and nationality. The teachers are from different nationalities: They are as follows: Omani 16, British 9, American 7, Indian 10, canadian 1, South African 1, Australian 1, Tunisian 1, Moroccan 1, Egyptian 1, Sudanese 1, and Polish 1.
Question 1: Does the unequal number of raters in each nationality affect the fit and bias analysis of the nationality facet?
Question 2: If yes, is there a way to run the analysis and look at the interaction between nationality and categories, for example, without having to reduce the number of raters, and stick only to those nationalities that are well represented?
Thank you for help
Bahrouni Farah
MikeLinacre:
Thank you for your questions, Barhouni.
"Does unequal number ..." - no. But the number of raters does. Many of your nationalities have only one rater. So your fit and bias analyses cannot claim to investigate "nationalities". They are investigating individual raters and the examinees they happen to have rated.
Can you combine your raters into larger national groups? For instance:
Omani+Tunisian+Morrocan+Egyptian+Sudanese
British+South African+Australian+Polish
American+Canadian
Indian
or whatever makes good sense in your situation.
bahrouni:
Thank you.
That sounds a good idea. I'll try it, with a new name though. I'll call that facet "Background" instead of "nationality". I will have 4groups in that facet: Arab Background, Native Background 1, Native Bachground 2, and Indian Background; and I will explain in the'Methodology Chapter' what each of those groups consists of.
Once again thank you very much
Bahrouni
MikeLinacre:
Sounds good, bahrouni.
767. Facets and ConQuest workshops
Jade April 24th, 2009, 8:57pm:
PROMS 2009 offers post-conference workshops on Facets and ConQuest. I am a beginning user of Facets. I am wondering if it is worth attending both the workshops. Could anyone here give some suggestions? It seems to me ConQuest can be used for more complex Rasch models. What prerequisite knowledge should I have so that I can make the most out of the workshops? Are there any books or articles that provide not so technical introduction to ConQuest?
Thanks
MikeLinacre:
ConQuest and Facets are intended for different types of Rasch analysis, Jade.
Facets aims at datasets with persons-items-raters, such as essays and oral examinations.
ConQuest aims at large-scale datasets which may be very sparse or multi-dimensional such as TIMSS. ConQuest is more technical than Facets, but both are technical.
I don't know of a less technical introduction to ConQuest. Does anyone ?
Jade:
Thank you for the clarification, Mike.
768. Changing scale direction
Raschmad April 19th, 2009, 4:55am:
Dear Mike,
How can I change the direction of person measure and item measure scales in Winstpes?
I mean, I want the items with highest raw scores to have highest logits and persons with highest raw scores to have lowest logits.
Tanx
Anthony
MikeLinacre:
Anthony, there are two ways to change the scale direction, and to keep the raw scores unchanged:
1. USCALE = -1
or
2. Transpose the data matrix:
use the Winsteps "Output Files", "Transpose"
analyze the transposed file
connert:
If you save the person file as a file for a statistical analysis package then you can modify the values within the statistical package. For example, if you save the person file as an SPSS save file then you can simply modify the values of "measure" by multiplying by -1. Be sure to notate this in the label information.
769. Analysis Plan-different likert scale, same item
pjiman1 April 16th, 2009, 3:26pm:
I am trying to come up with an analysis plan for evaluating the use of different likert scales for the same question. For example, due to variations in survey adaptation, we have the following questions asked in different ways and using different likert scales (Students did not answer each version of the question. Due to mishaps here and there, each student got only one version of the questionnaire):
1. Students in my classes usually follow the rules, 1-5 SD - SA
1a. Students in my classes usually follow the rules, 1-4 SD - SA
2. In my classes, there are many noisy and disruptive students, 1-5 SD - SA
2a. In my classes, there are many noisy and disruptive students, 1-4 NEVER - ALL OF THE TIME
3. I feel like I am an important part of this school, 1-5 SD - SA
3a. I feel like I am part of this school, 1-5 SD - SA
The difference between item 1 and 1a is that one uses a 5 pt likert scale, the other uses a 4 pt. The difference between item 2 and 2a is that the one uses an opinion scale (strongly disagree to strongly agree) and the other uses a frequency scale. The difference between item 3 and 3a is a slightly different wording.
My task is to determine if these items and likert scales provide equivalent information. I am reviewing the literature for ideas on an analysis plan. Thus far I am thinking of examining the variance of the items, comparing alpha coefficients, looking at descriptive statistics and category use. I am also taking a RASCH approach to examining the rating scale categories of these items. I was wondering if others had ideas about examining the equivalence of these items and likert scales.
Thanks in advance.
Pjiman1
MikeLinacre:
Here is one approach, Pjiman1.
Are these 3 items the entire questionnaire, or examples of more items on the questionnaire?
1. Let's assume they are representative examples of all the items:
2. Let's assume the two groups of students are randomly equivalent (same standard deviation).
3. We perform two separate analyses, grouping the items within the questionnaires according to their rating scale definit
3. We look at the person reliabilities from each analysis
4. The reliability from 3 5-category items is R. The average number of categories per item is 5, so the average number of decision points per item is 4.
5. The reliability from 2 4-category items and 1 5-category item is Ra. The average number of categories per item is 4.33, so the average number of decision points per item is 3.33.
6. Then, using the Spearman-Brown Prophecy formula, we predict that:
Ra(predicted) = 3.33 * R / (4 + (4-3.33)*R)
If Ra is less than Ra(predicted) then the "a" questionnaire is less reliable than the other questionniare, and vice-versa.
When investigating the functioning of individual items, we like to see an orderly advance in the use of the categories. My own preference is to look first at the "average measures" for each category for each item, but other experienced analysts have different preferences.
770. Invariant scale structure over time
pjiman1 April 16th, 2009, 3:29pm:
Hello,
I was wondering about how to examine if a RASCH scale structure is invariant over time. In my discussion with Nikolaus Bezruczko, he mentioned that it is important for a RASCH scale structure to be rigid over time. I have three waves of data for a scale. I divided them into the three waves and examined the RASCH stats separately. I noticed some items have better fit stats depending on the wave. Also, some items stay on their dimension at each wave, other items bounce from dimension to dimension.
Is there a method to determine if a scale structure is invariant over time with each administration? Would rack and stack procedures give me insight into this?
Thanks in advance.
Peter
MikeLinacre:
Thank you for your email, Peter.
"items bounce from dimension to dimension." - This is alarming because it implies that the items belong to different latent variables at different times. This threatens the construct validity of the instrument, because we have lost the definition of what the instrument is measuring.
In general, we are most interested in the stability of the item difficulties across time. This can be investigated by "stacking" the data (items x 3 waves of persons) and then performing a DIF analysis of items vs. wave.
But there are situations in which we expect to see changes in item difficulty. For instance if the treatment is item-specific. We see this in medical rehabilitation where treatment is aimed at patient deficits. Or in education, when there is "teaching to the test". We can then identify the impact of this item-specific activity by "racking" the items (3 waves of items x persons), and seeing the change in item difficulty as the effect of the treatment.
771. basic Facets questions
william.hula April 14th, 2009, 6:48pm:
I have a few basic questions about a potential Many-Facets Rasch analsysis. We are administering a set of rating scale items assessing communication activity limitations to a group of patient- and proxy-respondent pairs. Each patient and their associated proxy will respond to all of the items. Each patient will respond only for themselves and each proxy will respond only for their associated patient. We are not at all certain that the patient and proxy respondents will produce similar item hierarchies, although it may be the case.
Questions:
1. Is this design amenable to a Facets analysis with item, patient, and rater (self, proxy) as facets?
2. Is there a connectedness problem with this design?
3. Will a Facets analysis speak to the issue of whether patient and proxy responses can be meaningully calibrated to a common scale?
Many Thanks.
MikeLinacre:
Thank you for your questions, William.
1. This analysis could be done with Facets, but see 3.
2. Raters nest within patients, so this design would need group-anchoring of raters to be connected.
3. This could be done with Facets using its bias-analysis feature, but a simpler approach would be to do a DIF analysis with a simple rectangular dataset in Winsteps (or equivalent software).
Columns are items
Rows are patients-raters: code each data record with a patient id and a rater id and a rater type.
Do a DIF analysis of item x rater type.
Inconsequential DIF indicates the raters share the same scale.
If there is a core of items without DIF, then these can form the basis for a common scale, the DIFed items then become different items for the two rater types:
Items
xxxxxx rater-self
xxxxxx rater-self
xxx xxx rater-proxy
xxx xxx rater-proxy
You could also use the Winsteps "Subtotal" reports to see how much rater-types differ in their "leniency" of rating.
772. DIF effect sizes
JCS April 8th, 2009, 11:30am:
I'm trying to understand the DIF output better. I ran the Winsteps DIF analysis and then also ran an external Mantel-Haenszel analysis for comparison. All my level-C DIF from the external MH were also flagged by Winsteps, but Winsteps flagged many, many more items based on statistical significance. I realize this is due to my sample size so I want to get an effect size that's comparable to the ETS scale so I can match up my external MH output with the Winsteps output (and to make sure I'm understanding things correctly). Here are my questions:
1) If the DIF contrast = ln(a), then can't I just multiply the DIF contrast by -2.35 to put it on the ETS delta scale?
2) Is the Mantel-Haenszel "size" supposed to be the same thing as ln(a)? If so, why aren't the values the same as the DIF contrast values?
MikeLinacre:
Thank you for your questions, JCS.
1) Yes. The EST delta scale = -2.35 logits.
2) MH and the Winsteps DIF contrast are both log-odds estimators of DIF size. For the DIF contrast, each person is a separate case (so that missing data can be accommodated). In the MH method, the persons are stratified by ability levels (raw score group) into 2x2 cells. In the MH method, if there are strata with 0 persons in a cell, then the strata may be omitted or combined with adjacent strata. These actions may reduce the reported DIF size and its significance.
JCS:
Thanks, Mike! This actually clears up a lot. By the way, this is a great service and I appreciate ALL your comments/replies on the forum.
JCS:
Actually, a follow-up question: to what extent are the DIF contrast results affected by non-normal ability distributions in the two populations? Both ability distributions are positively skewed and leptokurtic (confirmed by statistical tests).
MikeLinacre:
Neither DIF-Contrasts nor MH make any assumption about the sample distribution, JCS.
JCS:
From the "Mantel-Haenszel DIF and PROX are equivalent" article in Rasch Measurement Transactions (1989) you noted "Thus whenever the ability distributions of the reference and focal groups are approximately normal, PROX can be used for estimating and testing the magnitude of item bias."
Maybe I'm misinterpreting this article or statement.
773. factor analysis
bahar_kk April 8th, 2009, 6:57am:
when we use factor analysis method in IRT model
and why?
thanks
MikeLinacre:
Perhaps http://takane.brinkster.net/Yoshio/p026.pdf will help, Bahar_kk.
Does anyone have other suggestions?
connert:
Another suggestion:
R. J. Wirth and Michael C. Edwards. "Item Factor Analysis: Current Approaches and Future Directions" Psychological Methods 2007, Vol. 12, No. 1, 58-79
774. Generat Data set
bahar_kk April 5th, 2009, 7:11pm:
hi
I m studying my thesis( estimate ability with Neural Network so that NN is replaced to IRT model) ,i need to data set ,how can generate data set? i ve heart that Hugin Lite is alternative to generate Data set,is it right?
have every body ready Data set that has used in her/his project and send for me??
thanks ur reply
MikeLinacre:
Thank you for your request, Bahar_kk.
Hugin Lite can simulate data based on a specified neural network.
If you want to simulate data based on a set of Rasch measures, software include WinGen, WinIRT and Winsteps.
If you need a pre-existing dataset, there are many available. Please tell us more details about what you need.
bahar_kk:
HI
thank u so much ur reply
i want to use NN to estimate ability of examinee.then i will compare my result to IRT model that how many classify correctly as compared IRT. estimate of ability by IRT model will be target value of NN (supervised learning)
ok.i need a data set to train NN ,i need response pattern for input of NN for train.
how provide Data set.
i heart that Hugin Lite generate data set,i want to use param_3PL to estime ability and parameters.
is it good program ? what is ur idea?
thanks agian
MikeLinacre:
Thank you for this information, Bahar_kk.
For 3-PL IRT, you will need to generate dichotomous (0-1) data. The 3-PL estimates will be item difficulty, item discrimination and item guessability (lower asymptote). The person sample-distribution is usually assumed to be N(0,1).
For reasonable 3-PL estimation, you will probably need at least 50 items and 500 persons which appears to be the maximum for Hugin Lite.
http://echo.edres.org:8080/irt/param/ is freeware for 3-PL estimation.
bahar_kk:
hi
sorry,u didnt say me ,how generate data set?
which program is better param_3pl ,bilog, wingen
thanks a lot
bahar_kk:
you means that i can use hugin Lite to generate data set?
i want to use 500 examinee and 20 item to test NN and estimation person and parameters.
MikeLinacre:
Bahar_kk, what do you want to do?
Simulate data which fits an NN model - then Hugin Lite can do this.
Simulate data which fits a 3-PL model - then WinGen can do this.
Estimate NN parameters for a dataset - then Hugin Lite can do this.
Estimate 3-PL parameters for a dataset - then Param_3pl and Bilog can do this.
Neural network datasets: http://www.fizyka.umk.pl/~duch/software.html
IRT datasets: http://bear.soe.berkeley.edu/EIRM/
bahar_kk:
hi
i need data set that can train NN ,i want to be response pattern (0,1) then these data will be used input of NN and also use IRT software.
NN data set is not suitable because i need data saet like response pattern (0, 1) it is like matrix that num of column is num of items and num of row is num of examinee.it is special data and can not use internet to download.IRT model that i want to use ,is dichotomous model.this data set will use input of NN also will be used IRT model and will be compared IRT and NN
thanks alot ur reply
MikeLinacre:
Thank you, Bahar_kk. We hope that your project succeeds.
775. softwares of IRT models
bahar_kk April 6th, 2009, 3:48pm:
hi every boddy
i want to know which software of IRT model is good.i have investigated Param-3pl but it is very simple( no chart, no plot,..) why?????
i need a software that has plot also i could import data set it
please guide me
i m beginner to IRT model. :'(
MikeLinacre:
www.assess.com has IRT software, Bahar_kk.
776. Arabic Rasch Forum
edutests March 28th, 2009, 2:00pm:
Can you visit my Arabic Rasch Forum ? And can you help me ?
This is the link:
http://raschmodels.11.forumer.com/
Please visit it and support me
777. The differences between winsteps and Bigseps
edutests February 28th, 2009, 1:49pm:
i will use Bigsteps to analysis testlets by pcm , what is the differences between bigsteps and winsteps
MikeLinacre:
Thank you for asking, Edutests.
Bigsteps was the precursor to Winsteps. www.winsteps.com/wingood.htm lists all the changes in Winsteps that go beyond Bigsteps.
But, if you run Winsteps in the same way as Bigsteps (from the DOS prompt without interactive features) the estimated measures and fit statistics are the same.
edutests:
thank you , prof. mike linacre
778. Variance explained for assessment of dimensionalit
erica11 March 10th, 2009, 12:05pm:
Hi, Rasch fans,I want to compare Rasch analysis and factor analysis in assessing the dimensionality of an instrument, can variances (unexplained and explained) and number of contrasts in Rasch analysis be used to this task?
MikeLinacre:
The "constrast" method was developed because factor analysis of the observations does such such an inferior job of detecting dimensionality, Erica11. See, for instance, https://www.rasch.org/rmt/rmt81p.htm
But, if you are experimenting, please be sure to include in your computations the variance omitted by factor analysis when the main diagonal of the correlation matrix does not contain 1's. This variance would form part of "unexplained variance".
erica11:
Thanks MikeLinacre, but I am still not quite clear whether "number of contrasts
above noise level" can be an indication of "number of dimensions" in Winsteps
MikeLinacre:
"Number of dimensions" - we need a clear definition of "dimension", Erica11.
If "any shared commonality not on the Rasch dimensions" is defined to be another dimension, the "number of contrast above noise level" is an indication.
But what is the noise level for your data? To discover this, simulate several datasets that match your datasets, but that fit the Rasch model. Winsteps SIMUL= does this. Analyze those datasets. Perform dimensionality analyses. These will tell you what the noise-level is.
But we usually define a "dimension" in empirical data more strictly. We require the commonality to have a meaning. It is the "xxx" dimension, where we can explain what "xxx" is. If we can't explain it, then it is an accident of the sample, not a dimension. See "too many factors" - https://www.rasch.org/rmt/rmt81p.htm
779. Facets with fixed parameters
mlavenia March 19th, 2009, 4:02am:
Hello all - I am part of a study where I think a facets model might serve as a useful analytic strategy, but am unsure about a couple of points and welcome your input: We have a randomized design which will look at ability to rate videos of classroom instruction as an outcome. We will likely use the usual CTT statistics to look at pre-to-post change, such as intra-class correlation and Cohen�s Kappa; however, it seems like an analysis if rater severity might be very interesting. Here is my question: the videos will be pre-judged by a panel of experts (using a 25 item, 5-point Likert scale protocol that scales the instruction on its degree of �reform�). We are interested in whether our treatment makes an improvement in our subjects� ability to rate the videos similarly to that of our experts. My understanding of the many-facet Rasch model is that this would require estimating the video�s ability and item difficulties based on the experts� scores, and then fix those parameters, whereby when we run the model with the subjects, only the parameters for their severity are estimated. This opens a number of questions: (1) is this even possible (does the FACETS software allow some parameters to be fixed); (2) if so, does this even make sense as an analytic strategy; (3) if not, what would. Essentially, the CTT stats I mentioned above can tell us whether our treatment was able to reduce the between subject variance and increase the subjects' rate of agreement with the experts, but not tell us anything about its impact on rater severity. Maybe it has no mean impact on subject-expert agreement (i.e., subjects' "rating expertise"), but does make the subjects more or less severe in their ratings. Thus, the MFRM presents itself as a tantalizing option; I am just struggling with how. Any and all feedback will be greatly appreciated. Sincerely, Mark
MikeLinacre:
This sounds a great project, Mark. Thanks for asking.
The simplest analysis would be to score each rating by a subject: 1 if it agrees with the experts, 0 if it disagrees. Then the analysis would produce measures of "agreement with the experts". We would expect to see this improve after training.
Next, you might want to discover the direction of improvement. Use a 5 point-rating scale:
3 if the subject agrees with the expert;
4 if one more than the expert;
5 if two (or more) more than the expert;
2 if the subject is one less than the expert;
1 if two (or more) less than the expert.
This would tell us if the subjects are under or overshooting the experts (rater severity).
As outlined here, these two analyses require two facets (rectangular datasets, i.e., suitable for standard Rasch software): the rows are subjects and the columns are videos. Each subject would be in the data file twice: pre- and post-. You could then produce scatterplots, subtotals and DIF studies to see what has changed between pre- and post-training.
How does this sound, Mark?
Yes, and Facets can have fixed (anchored) parameter values, but I recommend Winsteps, rather than Facets, whenever possible.
mlavenia:
Hi Mike - Thank you so much for your responsiveness. That sounds great; let me make sure I understand though. I didn't make it clear in my post, but the subjects will be using the same protocol that the experts will; thus, I'm assuming that that matrix would now be 51 columns wide (subjectid + the 25 items X 2 administration). In addition, the pre and post sessions will consist of rating several videos; would you recommend that analyses are run separately for each video or would there be a computational benefit in accounting for all ratings (it seems like we might be running into a local independence problem if we do not do them separately--in fact I would have thought that simply running a pre and post in analysis would be a violation). [Please bear with me; I am very new at this and have yet developed a very nuanced understanding of all of this.]
If I hear you correctly, you would recommend that we devise a true score (either through having our experts reach a consensus, or simply calculate the arithmetical mean of their individual ratings); whereby, we would then recode each subject's ratings as you described. Then, if I understand correctly, the ability estimate (computed by Winsteps) would be interpreted as an indicator of severity (>0 indicating degree of severity; <0 indicating degree lenience). I'm not quite sure how the pre and post would be used in this way, unless we calculated abilities (severity) separate for each pre and post, and then compared them. Furthermore, what would be the interpretation of the difficulty parameters in this framework?
[If my questions are now verging on the need for paid consultation, please forgive me. I am grateful for any degree of assistance your time permits.]
Lastly, I currently have the Bond & Fox version of steps and facets; will this be adequate for my analysis? We have approx. n=250 subjects.
Thank you for your time and consideration, Mark
MikeLinacre:
Thank you for your further explanatipon, Mark.
Local independence issues are usually not a concern in Rasch analysis. The easiest way is to analyze the data as though there is local independence, and then check the results to confirm that the data do approximate local independence.
Your data design is somewhat unclear to me, but analyze each subject as two separate people during the Rasch analysis, the pre-person and the post-person. The relationship between pre- and post- is a finding of your study. Do not impose that on the analytical design in advance.
For your experts, either they must agree, or you can take the median of their ratings as the "standard" rating of each video. The mean is fractional. You need an exact "standard" rating. If there is not a "standard" rating, then your analysis will become too complicated.
Your analytical design does not appear to match Facets. It will be rectangular: 25 items x (subjects at pre- + subjects at post-).
If you have 250 subjects, then you will have at least 250 x 25 x 2 observations = 12500. Another post in the Forum states that the limit for Bond&FoxFacets is 2,000. There is the freeware MS-DOS version of Facets at www.winsteps.com/facdos.htm which has much greater capacity.
mlavenia:
Hi Mike - Thanks again, ever so much. This will get us started; though I am quite sure that I'll be checking back in after we run it. Gratefully yours, Mark
780. obs%
seol March 18th, 2009, 5:53am:
Dear Dr. Linacre
Hi ! I'm seol. Recently, I compared OBS% using WINSTEPS with OBS% using FACET program with same data(Rater x item matrix).
the result indicate that the OBS% looks like quite different. hmm...
I attached two control file, in which the raw data is same. Could you check it for me?
One more question, Regarding paper (RMT 20(4), applying the rasch rating-scale model to set multiple cut-offs), in this case(rater x item analysis), what kind of model do I have to use? that is, rating scale model or facet model for raterxitem analysis ?
Thanks in advance.
MikeLinacre:
Thank you for asking this, Seol. You are using Winsteps and Facets to analyze the same data. Winsteps estimation requires fewer iterations than Facets for the same precision. I must update the Facets estimation algorithm with the recent improvements in Winsteps.
You asked about Obs%.
Winsteps: Obs% indicates "for this rater, match between the observed category and the expected category value (based on the item difficulty and the rater leniency)"
Facets: Obs% indicates "for this rater, match between the observed category and the category awarded by another rater on the same item".
We would expect the Winsteps Obs% to be much higher than the Facets Obs%, because the Winsteps Obs% is the same as "for this rater, match between the observed category and the category that would be awarded by a perfectly predictable rater (of the same leniency as the target rater) on the same item".
Is this clear?
https://www.rasch.org/rmt/rmt204a.htm "Applying The Rasch Rating-Scale Model To Set Multiple Cut-Offs". The analyses mentioned in that research note are all 2-facets. They can be successfully accomplished with Winsteps.
seol:
:)
Many thanks to your ALWAYS kind reply. ^^
781. Repsonses Cut off
Munshi March 17th, 2009, 7:11am:
Hi, I have a large data set with the following:
Total non-blank responses found = 24404
Number of blank data lines = 46
Bond&FoxFacets: responses cut off at = 2000
Valid responses used for estimation = 2000
The problem is only 2000 responses are analyzed, how can I increase the Bond&FoxFacets: responses cut off to say = 24000
When i run the analysis, only the first 2000 responses are analysed, any suggestions ?
Thanks
Regards,
Fadi
MikeLinacre:
Thank you for your question, Fadi.
Bond&FoxFacets is designed for the analyses in the Bond & Fox book.
You can:
purchase the full version of Facets www.winsteps.com/facets.htm
or
use the free "MS-DOS" version of Facets www.winsteps.com/facdos.htm
Munshi:
Thanks Mike for your promt reply.
Regards,
Fadi
782. Item calibration
danielcui March 16th, 2009, 9:45am:
Hi Mike,
I encounter a problem when use item measure as item calibration value. Sometime it shows the number from 0 to 100, while on another occasion it shows from + number to - number(see attachment). how could this happen?and which number I need to choose? Thanks
Daniel
MikeLinacre:
Thank you for your question, Daniel.
Your Winsteps control file includes:
UIMEAN = 50 ; item mean for local origin
USCALE = 10 ; user scaling for logits
Based on these instructions, your reported Rasch measures will have an approximate range from 0 to 100 = logits * 10 + 50
But the internal processing of Winsteps is done in logits, so that the Convergence Table reports the values in logits.
Does this explain the differences you see?
784. 1-item rating scale
limks888 March 6th, 2009, 3:15pm:
Hi Mike,
I'm curious about rating scale that consists of a single item only.
I have come across single-item 5 point, 7 point or 9 point Likert scales that purportedly measure a single construct.
Is a single-item scale necessarily unidimensional?
Can a Rasch analysis using fit and separation statistics be performed on person responses to the scale to assess whether the data fits the Rasch model?
What are the constraints of such a scale?
Thank-you.
Lim
MikeLinacre:
If each construct (latent variable) is only measured using one item, Lim, then there is no information in the data for investigating dimensionality or the functioning of the rating scale.
An essential aspect in science is "replication". One experiment (or one item) can be exciting (like the "cold fusion" experiment), but it must be repeated under slightly different conditions for it to be convincing.
So that one item may be exciting, but we need another item to verify that we are measuring what we intend to measure, and to start to measure the construct. One item can only order the construct.
But, if the persons can be thought of as representative of a specific type of person, then the persons can provide the replication. See "stress after three mile island" https://www.rasch.org/rmt/rmt54n.htm
limks888:
Thank-you Mike for your explanation.
Lim
785. Reverse thresholds
RS March 3rd, 2009, 11:53pm:
Dear Mike & others
A computer test with 55 items (multiple choice, short answer & extended response) is given to 10000 Grade 10 students. The extended Logistic Model of Rasch (Andrich, 1978) was used with the computer program RUMM to construct a scale. The initial analysis indicates that there are eight items with reverse thresholds. After checking the marking key and category frequencies for these items, it was decided to collapse some categories. The second analysis (after recoding the items with reverse thresholds) shows that there is no reverse threshold at all. However, the fit statistics indicate that the item fit residual for these eight items has decreased dramatically, indicating over-discrimination. In other words, these items, which previously had a good fit; do not fit the model now. So the questions are:
Is it legitimate to collapse categories by considering the marking key and frequencies for each category only?
What is the impact of these over-discriminating items on the scale?
What is the relationship between item fit statistics and reverse thresholds?
Why those items with reverse thresholds fit the Rasch model relatively well?
Many thanks & regards,
RS
MikeLinacre:
An interesting and important set of questions, RS.
First, let me ask and answer a question:
0. Why are some thresholds reversed?
Answer: Reversed thresholds occur when there is an intermediate category with a relatively low frequency. This can happen for several reasons. Usually it is because the category represents a relatively narrow interval on the latent variable. For instance:
Please estimate the relative heights of the Sears Tower and Taipei 101 to their highest points. The Sears Tower is
A. much higher
B. a little higher
C. exactly the same
D. a little lower
E. much lower
If we surveyed international travellers about this, we would expect very few responses in category C, "exactly the same". This represents a very narrow interval on the latent variable. Its thresholds would be reversed.
Now we can answer your questions:
1. Is it legitimate to collapse categories by considering the marking key and frequencies for each category only?
Answer: That is a good start, but we usually need to do a more thorough investigation.
A. The categories: these must be "exclusive, extensive, exhaustive"
exclusive: not over-lapping
extensive: represent an interval on the intended latent variable
exhaustive: cover the entire range of the latent variable
and they must also be scored in numerically-ascending qualitative levels of the latent variable.
B. Frequencies: the relative frequencies of the categories must make sense in relationship to their meanings and location on the latent variable.
For robust estimation, we need at least 10 observations of each category.
C. Average category measures: Rasch theory is that:
higher categories --> higher measures
higher measures --> higher categories
We can verify this in the data my computing the average ability measure of the persons who respond in each category. This should ascend as the category numbering ascends. If an "average category measure" decreases when the category number increases, then the sample of persons disagrees with our numbering of the ordered qualitative levels of the rating scale. We must return to A. and re-examine our thinking.
D. The responses in each category should be those expected for the category. We can confirm this by computing a summary fit-statistic for the observations in each category. If the observations in a category misfit, then perhaps the category is ambiguous or off-dimension. Categories like this are "Don't know" and "Not applicable".
E. Your action must make sense to the audience to whom you will communicate your results. In the "Sears Tower" example, collapsing "exactly the same" with another category would not make sense.
2. What is the impact of these over-discriminating items on the scale?
Answer: Over-discriminating items are too predictable. Their effect on measurement is to increase the logit distances between measures. Collapsing the categories has reduced the randomness in the data which is used by Rasch analysis to construct the measures.
In the Sears example, collapsing category C removes an option, and so increases the predictability of the data.
3. What is the relationship between item fit statistics and reverse thresholds?
Answer: In Rasch theory, item fit and reversed thresholds are independent.
If the reversed thresholds are caused by a narrow category that is part of the latent variable, then collapsing the threshold will cause overfit.
But if the reversed thresholds are caused by a category which is not part of the latent variable (such as a "Don't know" category in the Sears example) then it will cause misfit. In this case, it would be more productive to code the "Don't know" category as "missing data", than to collapse it with another category.
4. Why those items with reverse thresholds fit the Rasch model relatively well?
Answer: because the low-frequency categories correspond to qualitatively-advancing intervals on the latent variable.
Does this help you, RS?
RS:
As always, thank you very much for you comprehensive and inclusive response.
I have got one more question to ask: What does differentiate Thurstone thresholds from Andrich thresholds?
Many thanks & regards,
RS
MikeLinacre:
In psychometrics, Thurstone thresholds came first, RS.
Thurstone threshold = location at which (probability of all categories below) = (probability of all categories above)
Andrich threshold = location at which (probability of category immediately below) = (probability of category immediately above)
RS:
Great. Thanks a lot.
786. Mixed Item Types
connert March 5th, 2009, 9:15pm:
Will Winsteps handle analysis of test results with mixed item types? And what is a good reference about how to deal with mixed types?
MikeLinacre:
Winsteps can analyze a variety of item types simultaneously, Connert. Relevant Winsteps control instructions are
ISGROUPS= www.winsteps.com/winman/isgroups.htm
and IREFER= www.winsteps.com/winman/irefer.htm
connert:
Thank you Mike! I searched the manual but obviously used the wrong terms.
787. calibrating results from CATs
Stampy March 3rd, 2009, 11:27pm:
Hi Mike,
I've been analyzing (using Winsteps) the results of a "testlet" based adaptive pilot test and am running into some problems based on how the test is administered. The test is made up of six discrete "testlets", each of which contains about 12 items. (Items within a testlet are considered independent.) All of the examinees take the same initial testlet, but are then routed to more or less difficult testlets based on their performance. (Testlet "difficulty" is currently defined according to the intended level of the items within them. The intention is to eventually use Rasch calibrations.)
The problem is this: The Rasch difficulty estimate of items in some of the "easier" testlets seem to be artificially inflated since only poorly performing students ever see those items. I was hoping that having all students take the same initial testlet would provide enough linkage across all students, but perhaps it isn't.
Short of rearranging the items and repiloting (which we intend to do) do you have any advice for analyzing the current results? Thanks.
MikeLinacre:
Is problem due to guessing, Stampy?
If so using CUTLO= would make sense. This trims out responses to items which are much too hard for individuals, i.e., responses on which low performers have a probability of success comparable with guessing.
This may also be a situation in which you need a 2-stage analysis:
1. Calibrate the items using only persons who are behaving appropriately.
2. Anchor the items at their calibrations from 1, and then measure all the students.
Stampy:
Thanks for your response, Mike.
It turns out that this particular problem was caused by user error :o. I had used a period (.) in the data file to indicate items that were not attempted (since this is an adaptive test). However, that period found its way into the CODES= specification when I created the Winsteps file from Excel. Since I was using an answer key in Winsteps to score the tests, the missing responses were treated as incorrect answers rather than missing data. Removing the period solved the issue.
MikeLinacre:
Yes, Stampy, somewhere on our test development team, "Murphy' is lurking ...
788. using the SEM
harmony March 3rd, 2009, 12:49pm:
Hello all:
This isn't exactly a Rasch specific question, but is related to the Standard Error of Measurement and how to use this statisic (or not) when looking at student test scores and making pass/fail decisions. I think I know the answer to the question, but would like some expert corroboration.
The situation is this: Students take a reading test of English language ability that has three different readings each with their own set of objectives based questions from those readings. One reading, however, performs very badly and proves to have been too difficult and little discrimination is fond between weak and poor groups. In many instances, in fact, the weak group has done better (probably from lucky guessing). This test also includes two listening tests.
Does it make sense, then, to use the SEM calculated from all reading tests (including the one that didn't work) and the listening tests to decide a few marks for borderline cases? Does not the poorly performing test taint the calculaion of the SEM?
Would it not make more sense to exclude the poorly performing test from the data entirely and calculate reading ability from the the two tests that were working and, if necessary, then apply a SEM from this calculation to borderline cases?
Thanks for any help!
MikeLinacre:
Thank you for your question, Harmony.
Almost certainly, the statistical computation used to produce the SEM is assuming highly (or even perfectly) correlated variables.
From your description, we definitely only want to include tests that "worked" in the decision-making. The test that didn't worked appears to be measuring a different latent trait (perhaps, "ability to guess effectively") so that including it with the other tests will include an uncorrelated variable, definitely increasing the measurement error (whether the SEM computation shows this or not).
harmony:
As always, thank you for your helpful reply! :)
789. Rasch in follow-up study
wlsherica March 2nd, 2009, 9:40am:
Dear Mike,
I had a baseline(time0) quality of life(QoL) assessment, Q0, followed by at
least one further assessment at a fixed time point following treatment(time1)
to obtain Q1.
Could I use Rasch to measure the change of QoL during a period of time?
Thank you so much~!
Cheers.
MikeLinacre:
Yes, you can, Wisherica! It was your type of analysis which motivated Georg Rasch to develop his model.
Q0 is the benchmark data. So please follow this procedure:
1. Rasch-analyze the Q0 data.
2. Form the Q0 output, obtain Q0 Rasch item difficulties and rating-scale-structure "thresholds".
3. Rasch-analyze the Q1 data with the item difficulties and thresholds anchored (fixed) at their Q0 values.
4. Now all the subjects have been measured on the Q0 "ruler", and the subject measures can be compared using the usually statistical techniques (such as subtracting Q0 measures from Q1 measures to obtain the change for each subject).
An advantage of using Rasch over raw scores is that the non-linearity of raw-scores is eliminated. In raw-scores terms, changes in the middle of the score-range always look larger than changes at the ends of the score-range. Rasch adjusts for this.
OK, Wisherica?
wlsherica:
Thank you for your reply, Mike~!
Does it mean I could use Winsteps to handle this ?
After getting Q0 Rasch item difficulties and thresholds, how to anchor them ?
(I'm confused about how to anchor something for so long.)
Thank you so much!!
MikeLinacre:
This is straight-forward in Winsteps, Wisherica.
Add to the Q0 analysis control file,
IFILE=Q0if.txt
SFILE=Q0sf.txt
Add to the Q1 analysis control file:
IAFILE=Q0if.txt
SAFILE=Q0sf.txt
That is all that is needed!
wlsherica:
Thank you for replying in detail, Mike.
If I didn't misunderstand the analyzed procedure you provided, I tried to write it out
as follows:
�u3. Rasch-analyze the Q1 data with the item difficulties and thresholds anchored (fixed) at their Q0 values.�v
�� So I add the order
....
IAFILE=Q0if.txt
SAFILE=Q0sf.txt�v
.....
in to Q1 file, then run it.
Which table(s) or graph(s) do I need to check ?
If the procedure was correct, why I need to add the code as follows in Q0 file?
.....
IFILE=Q0if.txt
SFILE=Q0sf.txt
.....
Thank you so much.
MikeLinacre:
Wisherica, please do the Q0 analysis before the Q1 analysis.
The files Q0if.txt and Q0sf.txt are output files from the Q0 analysis.
They are input files to the Q1 analysis.
You will see if they have been input correctly, because the letter "A" will appear on the item reports next to the item difficulty measures.
seol:
;) Dear Dr. Linacre
This is interesting approach for longitudnal study using Rasch measurement.
I have a quick question about this.
If I have Q1, Q2, Q3 data during a period of time, What kind of approach can I use to compare subject measures during a period of time?
Thanks in advance. :K)
MikeLinacre:
Seol, you have some decisions to make. Which time-point is the most important?
In medical applications, it is usually the first time-point, when treatment decisions are made.
In educational applications, it is usually the last time-point, when pass-fail decisions are made.
In survey applications, each time-point may be equally important.
In general,
1. analyze the data from the most important time-point. Generate files of item difficulties and rating-scale thresholds.
2. analyze all the data in in one combined analysis with the item difficulties and rating-scale thresholds anchored at their values from 1.
3. In the combined analysis, flag each person record with its time-point, you can then produce sub-totals for the persons by time-point, and do DIF analysis by time-point, so that you can track what has changed across time.
OK, Seol?
790. Misclassification
cbwheadon February 27th, 2009, 11:22am:
I am interested in misclassification around cut-scores and have often used the memo: https://www.rasch.org/rmt/rmt123h.htm as a rule of thumb. However, I have been playing about with Gulliksen's 1950 method http://www.ncme.org/pubs/items/16.pdf and trying to conceptualise how Rasch accomodates some of Gulliksen's criticism of using SE +/- 1. In particular, for extreme scores, Gulliksen's assertion that a candidate's true score is likely to be between the mean score and the obtained score. This shifts the axis of symmetry for misclassification.
Is this something we have to worry about with Rasch?
MikeLinacre:
Thank you for pointing out that paper, cbwheadon.
Rasch has several advantages over Classical Test Theory. One is that we have an individual standard error for every person and item. We don't work backwards from a summary reliability estimate.
Rasch also makes the adjustment that the measure corresponding to an extreme (zero or perfect) raw score is between the "observed measure" (infinity for Rasch) and the more central measures.
So it seems that both of Gulliksen's concerns are already satisfied by Rasch.
cbwheadon:
Thanks Mike. Is the adjustment you refer to the fundamental ogive exchange of score for ability?
MikeLinacre:
Cbwheadon, the Rasch extreme-score adjustment makes extreme scores more central by 0.3 score-points or so. This gives to each extreme score a Rasch measure noticeably, but not ridiculously, more extreme than the Rasch measures corresponding to non-extreme scores.
cbwheadon:
Mike,
Thank you for the clarification. Looking at some data it seems the Gulliksen method produces similar results to the Rasch model when the reliability is reasonably high. According to both models, when the cut-score is above the mean the confidence interval is wider (in terms of raw scores) below the cut-score than above it. As reliability dips below .9, however, the intervals produced by Gulliksen's method seem far too wide. It seems to me that he is attempting to counteract what you've termed the raw score bias against extreme scores, but this only works if the tests are reasonable well targeted. Do you think I'm on the right lines?
Regards,
Chris.
MikeLinacre:
Your obsverations are astute, Christ. Rasch and CTT raw-score reliability are assessing different aspects of performance. Rasch is attempting to quantify the reliability (reproducibility) of measures on the latent variable. CTT is attempting to quantify the reliability (reproducibily) of the raw-scores which manifest those locations on the latent variable.
Rasch and CTT reliability are usually almost the same when the items are targeted on the sample. But as the raw scores become more extreme, Rasch reliability usually decreases (because the locations of the persons on the latent variable become less precise) and CTT reliability usually increases (because the observable range of raw scores for each person decreases). It seems that Gulliksen is trying to make a Rasch-style adjustment in a pre-Rasch world.
791. Unidimensionality and local independence
Monica February 27th, 2009, 8:56am:
Dear Rasch Forum,
I have devised a pencil and paper assessment that attempts to measure students' knowledge of fractions. There are 47 items in total but only 43 used for the rasch analysis (using RUMM2020).
I understand that a critical assumption of the rasch model is:
(a) unidimensionality - the instrument focuses on one measure or attribute
(b) local independence - a person's response to an item is independent on their success or failure of any other item.
I have undertaken an examination of the residual correlation matrix produced by RUMM2020. I have found a number of items with residual correlations greater than 0.6. For example, item 14(a)asked students to shade 2/2 of a rectangle divided into 4 equal parts. 14(b) asked students to write another fraction for the part shaded. If students only shaded half of the rectangle in part (a), they wrote half for part (b). Hence I assume a clear case of local dependence.
However, I am unsure as to how to proceed with checking for unidimensionality and whether another Rasch analysis should be run without the items that violate local independence.
I have currently left the 8 items (4 pairs) that have >0.6 correlation in the residual principal component analysis. The first residual factor explains 5.86% of the common variance. Is this good or bad? Do I check the loadings after varimax rotation? Am I way off target???
Cheers,
Monica
MikeLinacre:
Thank you for your questions, Monica.
(a) unidimensionality - the instrument focuses on one measure or attribute.
Yes. More specifically, the instrument is dominated by one latent trait which can be represented as a straight line divided into equal interval units.
(b) local independence - a person's response to an item is independent on their success or failure of any other item.
Yes, but "local" means "after adjusting for the ability of the person and the difficulty of the item."
Yes, you have a case of local dependence. This suggests that those two items should be combined into one "partial credit" item which is scored 0-1-2. This compensates for the local dependence.
For the PCA of residuals, we don't want to rotate (VARIMAX etc.) because we want the first component to explain as much residual variance as possible (our analysis is confirmatory, not exploratory). Is the eigenvalue of the first component greater than 2.0? If so, this suggests that there are 2 or more items which are loading onto another dimension. You would have to look at the item-loadings on the first component to see what is going on in the data. Are there two clusters of items?
5.86% is low for the first residual component, but we would need to see the complete picture. 5.86% is only a wrinkle along the latent variable, too small to have an impact on the measurement.
OK, Monica?
Monica:
Hi Mike,
Thanks for your response. Just a couple more things.
From a theoretical perspective, students' knowledge of fraction equivalence incorporates understanding of a number of concepts (ie. identification of the unit, partitioning, appropriate use of pictures, understanding mathematical language). Does this muddy the water.
I have checked the other 3 pairs of items and each of the pair requires the application of the same fraction knowledge, but the success of item is not dependent on the other.
The eigenvalues for the first 3 components are greater than two and the 4th almost 2. The eigenvalues and % of total variance accounted for by each principal component is as follows:
1. 2.58 (5.86%)
2. 2.56 (5.81%)
3. 2.36 (5.36%)
4. 1.97 (4.47%)
What loading should I select to check which items are loading onto which components. When a loading of .3 is selected (principal component loadings) the first component has 5 items loading onto it. 3 items (positive loading) refer to fraction language and another 2 items (negative loading) refer to equivalence expressions, e.g. a/b = c/d. What does this mean in terms of person ability and instrument validity.
Cheers, Monica
ong:
Hi,
Monica wrote:
I have currently left the 8 items (4 pairs) that have >0.6 correlation in the residual principal component analysis
Mike response:
This suggests that those two items should be combined into one "partial credit" item which is scored 0-1-2. This compensates for the local dependence.
Is there a rule of thumb on the cut-off score for the standard residual correlation, to be combined and modelled as polytomous items? 0.6 to combine items and fitted to the partial credit model?.
Any literature written on this?
I have 28 items dichotomous items, where the residual correlation between pair s of dichotomous items where the standard residual correlations are as below:
0.96
0.94
0.88
0.84
0.83
0.77
0.75
0.62
0.58
0.57
0.56
0.55
0.51
0.4
When i explored fitting the data to the partial credit model for items with high residual correlation, the variance explained by the construct:
variance explained
10 PCM items and 8 dichotomous items 80.1%
11 PCM items and 6 dichtomous items 76.8%
12 PCM items and4 dichotomous items 76.1%
13 PCM items and 2 dichotomous items 73.7 %
14 PCM 73.4%
The variance explained decreased by combining more items to be modelled with PCM.
How can i explain this?
Should the data be modelled as PCM or a combination of PCM/dichotomous?
What criteria to make a judgement whether to combine items to be polytomous or to maintain them as dichotomous to account for local dependence?
Thank you
Regards,
Ong
792. Winsteps and Facets on the MAC
connert February 20th, 2009, 3:14pm:
Will Winsteps and Facets run on a MAC under Fusion VMware? Or other emulation software?
MikeLinacre:
Yes, Mac users tell me they do.
You have to be careful with text files because Mac and Windows text files have slightly different formats. The Mac handles this automatically, but sometimes it does not!
793. Rasch Model vs 3P IRT
RS February 16th, 2009, 11:40pm:
Hello Mike
A Science test with 45 multiple choice items is given to 25000 Grade 4 students. There are eight items from the Trends in International Mathematics and Science Study (TIMSS) in this test and the intention is shifting this Grade 4 Science scale onto the TIMSS 2003 scale.
I have used Rasch model to construct a single science scale while the TIMSS items have been calibrated using three parameter IRT where the three parameters are guessing, difficulty and discrimination. The Rasch model is the only measurement model which allows producing person-free item calibration and item-free person measure. So the questions are:
Is it legitimate to shift this Science scale onto the TIMSS scale?
How comparable are the item difficulties emerged from these two models?
Many thanks & regards,
RS
connert:
I am sure Mike will be way more tactful than I am. But the short answer is that by shifting you give up all of the real measurement properties of the scale. I don't know why some people don't get this. But they still insist on treating the analysis of measurement data from the perspective of quantification and model testing. The idea that the model is fixed because it is the only model that fits measurement criteria and you need to modify items and testing circumstances seems to not get past strong blinders. In some ways it is like persuading people that the earth revolves around the sun rather than the earth being the center of the universe. Anyway, there are any number of published articles that detail this argument. My personal experience is that the IRT crowd is not going away soon even though they should know better.
MikeLinacre:
Thank you for your questions, RS, and your comments, Connert. So true!
Since the raw TIMSS data appears to be freely available, http://timss.bc.edu/timss2003i/userguide.html, someone must have done a Rasch scaling of the TIMSS data by now. I suspect that ACER did one even before the 3-PL scaling was done.
In general, for well-behaved items and motivated students, cross-plotting the 3-PL and Rasch item difficulties produces a reasonable trend line. The problem is that it is not an identity line. But if you have your Rasch item difficulties, and the 3-PL item difficulties, you can cross-plot them, and discover a reasonable Fahrenheit-Celsius conversion from your scale to the TIMSS scale.
The problematic area for TIMSS is "motivated students". It would have been difficult to motivate the original students when the test had no consequences for them! Unmotivated students lead to high rates of guessing, response-sets, etc. These result in poor item calibrations, regardless of the analytical method. So you would also need to cross-plot your Rasch calibrations against any TIMSS Rasch calibrations you discover, because the relationship is unlikely to follow an identity line.
RS:
Thanks a lot Mike & Connert
I have plotted TIMSS locations against the Rasch item locations. (Please find attached the Word document). How do you distinguish between a trend line and an identity line?
Regards,
RS
MikeLinacre:
Thank you for the plot, RS.
Your central diagonal line is the identity line, but we can see that the trend is more horizontal because of the top-left and bottom-right points.
TIMSS and G4 disagree strongly about those top-left and bottom-right points.
Which set of measures makes more sense from the perspective of Grade 4 science ? This has to do with the construct validity of the test.
If the G4 item difficulties make more sense, then I suspect that there is so much guessing in the TIMSS data that the item estimates are close to useless.
But you can obtain a loose equating of the two measurement scales by
TIMSSed G4 measure = (mean of TIMSS items) + (G4 measure -mean of G4 items)*(S.D of TIMSS items / S.D of G4 items)
This formula applies to both persons and items.
RS:
Thank you for your comments Mike.
I have removed those items that did not function as common items between the TIMSS and the G4 Science scale from the link and treated them as unique items. As the attached plot shows the locations from these two scales now make more sense (with a R-square value equal to 0.91). Given this, can I shift the G4 Science scale onto the TIMSS 2003 Science scale using absolute anchoring?
Many thanks
RS
MikeLinacre:
RS, your plot looks as good as it gets in the real world. Congratulations!
Anchoring should work fine.
RS:
Thanks a lot Mike.
I have done the anchoring. The results indicate that this sample (n=25000) has performed extremely well on the TIMSS scale. The average scaled score is 582. This average is significantly higher than the average for those students, from the same country, who participated in the TIMSS 2003 examination. The average scaled score for this country was 510. Given that this sample is a representative sample, the question are:
1. Why the average for this sample is significantly higher than that for entire country?
2. Does it mean that the Science ability for this country has improved in the last five years?
3. Considering the measurement model that is applied in this study, how confident should I be in drawing such conclusion?
Regards,
RS
MikeLinacre:
For this you need a TIMSS expert, RS. You may find one if you post your questions on the Rasch Listserv. You can join it at www.rasch.org/rmt
RS:
Thanks a lot Mike. Will do.
794. Where is "Extra Specifications" line
erica11 February 17th, 2009, 2:13pm:
I am running Winsteps from SAS, but can not find where it is the Extra Specifications, could you help? Many thanks!
MikeLinacre:
"Extra specifications" is part of the standard Winsteps dialog, Erica11.
But "Extra specifications" will not appear if SAS is passing command-line variables to Winsteps, because these supersede the "Extra specifications".
Please go to the Winsteps "Edit" menu, "Edit Initial Settings", and make sure the "Extra specifications" is selected.
Do you see the "Report output file name?" prompt?
If so, you can go to the Winsteps "Edit" menu, and edit the Winsteps control file before the analysis.
erica11:
Thank you very much,MikeLinacre! Now the Now the problem solved!
795. Data selection exclusion values
lwarrenphd February 13th, 2009, 5:46pm:
Hello. I use WinSteps version 3.67.0 (11/27/08) on a Windows XP version 5.1 (Service Pack 2) operating system.
I have not been able to use the data value exclusion feature to specify data selection in my Winsteps control files.
For example, if I specify a selection value using "????{7}", the correct cases, those with a value of 7 in the 4th column, are selected. However, if I specify an exclusion value using "????{~7}", the exclusion is ignored, and all data are selected.
Can you help me with this? Thanks.
MikeLinacre:
Could be a bug in Winsteps, Lwarrenphd. I am investigating ....
lwarrenphd:
perhaps here is the misunderstanding ....
You wrote:
"????{7}", the correct cases, those with a value of 7 in the 4th column
Comment:
This is "7" in the 5th column (not the 4th column)
"????{~7}" means "not 7" in the 5th column.
YES. THIS WAS THE PROBLEM, AND MY ERROR. THANKS FOR YOUR QUICK AND HELPFUL RESPONSE! :D
796. common person equating and testing for differences
william.hula February 12th, 2009, 8:32pm:
Hello,
I have a question about the most appropriate procedure to use for determining whether persons have performed differently on two different tests that measure constructs that are (fairly highly) inter-related, but not necessarily identical.
I am using WINSTEPS and the Rasch model for dichotomous items to test whether individuals with language impairment performed differently on two different versions of a language test in which they indicated whether spoken word pairs are the same or different. The stimuli and correct responses are the same between the two versions, except that the second version imposes a short-term memory demand in the form of a 5 second delay inserted between the stimulus words. The expectation is that on average, participants will perform about the same or perhaps slightly worse on the second version, but that some may perform substantially worse, and some may actually perform substantially better. We are interested in identifying these latter two groups of people.
We have data from 70 people on the first version, and a subset of 55 on the second. I've run both data sets separately, and each seems to fit the Rasch model adequately when analyzed alone, as indicated by item and person infit and outfit statistics.
I followed the common person equating procedures described in the WINSTEPS Help file, and found that the two tests correlate at 0.64, >1 when disattenuated for measurement error. As the slope of the best-fit line was not so close to one (at 1.33) I used equating constants rather than concurrent calibration to place the second version on the same scale as the first in a subsequent re-analysis. This procedure identified 8 persons who performed differently at p < 0.05, 4 who performed worse on the second version, and four who performed better.
Recently, I read Schumacker and Smith (2007, Reliability: A Rasch Perspective, Educ & Psych Meas v67), wherein they recommended a procedure for evaluating test-retest and alternate forms reliability, and it occurred to me that this could be applied to my situation as well. This procedure is as follows: Calibrate the first test separately to obtain person scores. Next, analyze the second test (either second administration of the same test, an alternate form, or in my present situation, a different but related test) with the person scores anchored at their estimated values from the first test. Then, to evaluate which individuals have changed between the two tests, perform t-tests using the person ability displacement values divided by the model standard errors. When run on the data I described above, this procedure was more sensitive to differences: It identified 7 persons who performed worse on the second test, and 12 persons who performed better.
So the question is: Which procedure is more appropriate, or is there another better alternative that I've missed thus far?
Regards,
Will
MikeLinacre:
The purpose of your analysis is very focused, William. You want to investigate changes in person performance. You are looking for differences. Equating is likely to blur them. Schumacker and Smith suggest a productive approach, but it is easier this way:
1. For each person have one long response string: the fast test items followed by the slow test items (i.e., "rack" the data)
2. In the item identifying labels, put a code "F" as the first letter for all the fast items, and "S" as the first letter for all the slow items.
3. Perform a Rasch analysis of all the items together.
4. Perform a differential-person-functioning DPF analysis on the fast vs. the slow items using column 1 of the item label as the classifying variable.
5. The DPF analysis will show how the persons have changed between the fast and the slow.
Refinement: If you consider that either the fast or the slow test is definitive, then zero-weight the items of the other test: IWEIGHT=0 before doing step 3.
william.hula:
Mike,
Thanks much for the quick response. The approach you suggested (without the IWEIGHT command) gave very nearly the same result as the common person equating approach I took earlier.
However, when I set the item weights for the slow items to 0 (the fast items *could* be considered more deinitive), and produced the DPF table, there were no DPF measure estimates for the slow items. I gather from the help file that setting item weights to 0 excludes those items from calculation of the person estimates. Just want to make sure I didn't misunderstand something in your suggestion
Will
MikeLinacre:
Apologies, Will. I had forgotten that!
This suggests a two-stage approach:
1. Analyze fast and slow items with IWEIGHT=0, obtain IFILE=ifile.txt, PFILE=pfile.txt SFILE=sfile.txt
2. Analyze fast and slow items without IWEIGHT=, anchoring IAFILE=ifile.txt, PAFILE=pfile.txt SAFILE=sfile.txt
3. Perform a DPF analysis
797. How can I estimate the item step difficulties
ayadsat February 10th, 2009, 6:15pm:
I have used Parial Credit Model (PCM) and I have many items each of which has three categories (0, 1, 2) with known person ability and item difficulty. Moreover, I have assumed that the first item has 0 , -1, 1 step difficulties, How can I assume/estimate the step difficulties for other items, I dont like that the remaining items have the same steps, is there any procedure?
I thank u very much for your help!
Ayad,
??)
MikeLinacre:
Thank you for your question, Ayad. Estimating step difficulties (Rasch-Andrich thresholds) is complicated.
For PCM, if you know the item difficulty and the person abilities, then you also need the frequency of each category. The computation of the thresholds must be done iteratively, so you will need to use Excel (or Winsteps or something similar).
It is easiest to have Winsteps (or similar) do this for you, but you can write your own Excel formulae. Do you want to use Excel?
ayadsat:
Thank you for your answer, I dont know what is the frequency of each category, yes I would like to use Excel but I dont Know How to use it, can you give me example.
MikeLinacre:
Ayadsat, what data are you planning to use to estimate the step difficulties?
ayadsat:
In fact, I want to estimate the probability of person in order to estimate person ability using PCM by the following procedure:
https://www.rasch.org/rmt/rmt122q.htm
But, I dont have Rasch-Andrich thresholds. For Example I have the following data:
response difficulty
1 0.0938
2 -1.5000
2 -1.2500
0 -1.1667
0 -0.7500
2 -0.6667
1 -0.6000
1 -0.2400
1 -0.1667
2 0.1364
2 1.7000
2 1.7813
0 1.8750
2 2.1000
2 2.2500
2 2.5000
2 2.6250
2 2.7000
Thank you for reply,
MikeLinacre:
Is the first column the responses by one person, and the second column the item difficulties, Ayadsat?
This column has 18 items. Is that all the items?
How many columns of responses do you have?
If you have 25 items or less, and 75 persons or less, then use all the data with the freeware program Ministep: www.winsteps.com/ministep.htm
You can anchor the item difficulties using IAFILE=, and this will estimate for you the thresholds and the person abilities.
ayadsat:
Dear Sir, I am sorry about disturbance!
Yes, I have 18 items and only one person, I programed the PCM procedure by my self using PHP and I want to calculate the person ability at each row not all data at the same time.
for example by using my online program if the person response 1 to item 1 then I will find the his ability. Thereafter, if the person response 2 to item 2 the I will find the his ability at 1 and 2 responses respectively, and so on.
I need the procedure or another way to calculate the thresholds by my self.
I am sorry, I am not professional in English.
MikeLinacre:
Ayadsat, PCM models a different rating-scale for each item. You only have one observation for each item, so computing PCM thresholds is impossible.
You know the item difficulties. If you also know the person ability, then you can compute the thresholds for the RSM (Andrich rating-scale model) where all the items share the same rating scale.
The steps are:
1. Compute the frequency of each category in your response string for categories 0 to 2 (eg. 0=3, 1=4, 2=11, in your data above)
2. Set all the thresholds to 0.
3. Compute the polytomous probability of each category for each response (based on the known person ability, item difficulty, and thresholds).
4. Sum the probabilities for each category across the items to give the expected frequencies.
5. Adjust the values for all j=1,2 thresholds
new threshold(j) = old threshold(j) - ln(observed freq(j)/observed freq(j-1)) +ln(expected freq(j)/expected freq(j-1))
6. Loop back to 3 until changes in thresholds are very small.
798. Rasch alternative to ANOVA
limks888 February 13th, 2009, 7:51am:
Hi Mike, can you help me on this?
I'm planning to use Rasch analysis to study the effect of two fixed factors (A and B) on a dependent variable (Test scores). A and B consist of 3 levels each. The aim is to investigate whether there is a significant main effect/interaction effect on the test scores.
Can you suggest a possible procedure for such a purpose using Rasch methods if I do not want to use 2-way ANOVA?
Regards,
Lim
MikeLinacre:
How are your data arranged, Limks888?
Are they like this?
Case 1: A-level, B-level, Test score
Case 2: A-level, B-level, Test score
Case 3: .......
Or do you have more details for each Case?
limks888:
Dear Mike,
Thank-you for your prompt reply.
Yes, that is how I planned to arrange the data.
How would I then proceed to analyse such data?
Is there a better alternative arrangement?
Regards,
Lim
MikeLinacre:
Thank you, Lim.
Instead of "Test Score", the responses to the test would be better.
Then you could use a technique like "Rasch Regression" - https://www.rasch.org/rmt/rmt143u.htm
But this produces output that does not resemble a variance table.
799. facets control file question
connert February 12th, 2009, 1:48am:
I have a data set from 2004 proxy respondents who have assessed the physical disability status of their relative in long term care. I have data about about ability to do basic activities of daily living (ADLs) and instrumental activities of daily living (IADLs). The responses are dichotomous (can do without help, cannot do without help). The data itself is in an Excel file where rows are the proxy respondents and columns are particular activities. It is easy to set this up in Facets if you only have two facets (persons and items). But if I want a third facet to distinguish between ADLs and IADLs I cannot figure out how to set up the control file and the Excel data file. All the examples in the facets manual have additional facets specified in data in an additional column.
MikeLinacre:
Thank you for your question, Connert.
It sounds like you want a dummy facet so you can do something like a bias analysis of basic/instrumental vs. rater.
Here's how to do it.
1. Your Excel data file is probably OK as it is.
Facets = 3
Models = ?,?,?,R
2. Facet 2 would be all the items (ADL and IADL) numbered sequentially.
3. Label the Facet 2 elements:
2, Elements
1= A-description for each of the ADL items
....
12= I-description for each of the IADL items
...
*
4. Facet 3 is ADL or IADL
3, Instrument, A
1= ADL, 0
2= IADL, 0
*
5. Add a Dvalues= specification for Facet 3
Dvalues=
3, 2, 1, 1 ; element for Facet 3 is the first letter of label for element 2
*
6. Perform the analysis
800. Test Development Questions
MikeLinacre February 9th, 2009, 3:16am:
From a Discussion Board ....
I develop accreditation tests using CTT. We generally have the subject matter experts target the difficulty level of the items at the cut point between mastery and non-mastery. It seems that in Rasch measurement it is preferable to have items written to cover a broader level of difficulty than we use in CTT. This creates two issues for me.
1. It seems that the test developer really needs to decide prior to item development which method (CTT vs Rasch) to use. Have I exaggerated the problem?
2. We use a table of specifications to plan item development. Right away I'm worried about the unidimensionality assumption--but the table is what it is--it could perhaps be broken out into subtests, but this can involve 'political' complexities. Is this often a problem?
Related to this--If we have to vary the item difficulties (to use Rasch) then don't we have to write many more items at multiple difficulty levels for every table of specifications cell or worry that specific cells will become representative of difficulty rather than content?
3. I am under the impression that for accreditation tests a minimum of perhaps 250 examinees would be required (including a broad range of masters and non-masters), but it would really depend on how well the data fit the Rasch model.
MikeLinacre:
Thank you for these thought-provoking questions. But let me allay most of your concerns ....
You wrote: "subject matter experts target the difficulty level of the items at the cut point between mastery and non-mastery."
Yes, this is a good strategy. It is automated in computer-adpative tests. This strategy is usually easier to implement with Rasch than with CTT because the item hierarchy in Rasch is more clearly defined.
1. "Prior to item development"
There are basically two reasons for testing: measurement and classification.
If our focus is on classification (e.g., pass-fail) then we want lots of items near to the pass-fail decision point (for both Rasch and CTT).
If our focus is on measurement (e.g., so we can measure change during a course of instruction) then we want a spread of item difficulties from the lowest performance we expect to observe up to the highest performance we expect to observe. This is definitely easier to implement in Rasch than in CTT. In fact, it was the reason Georg Rasch to developed his model.
2a. "Unidimensionality"
If we are summing item responses into one total score, then we are assuming that the total score is the "sufficient statistic" for the responses. This is the same as assuming unidimensionality. The difference between CTT and Rasch is that CTT assumes unidimensionality but Rasch investigates whether it exists.
2b. "don't we have to"
Fortunately we are always in command! Rasch gives us more options than CTT. For instance, Rasch allows missing data. Rasch also gives us more powerful diagnosis of problems. But, if something can be done with CTT, it can also be done with Rasch, but usually better.
3. "a minimum of perhaps 250 examinees ...."
We have the same problem in CTT and in Rasch. How certain do we need to be about the difficulty (Rasch or CTT) of each item? If we need to be very certain, then we need a large sample. 250 examinees would be a good number. If we can allow ourselves to be less certain, then 30 relevant examinees is probably enough.
When do we need to be more certain? Here are some situations ...
1. When we have a test of only a few items
2. When the decision to be made is high-stakes
3. When the items are "partial credit"
4. When the items are considerably off-target to our sample.
5. When the unidimensionality of the items is suspect.
Again, the difference between Rasch and CTT is that Rasch tells us what is going on. CTT tends to assume that all is well.
The same situations arise (for both Rasch and CTT) when we need to decide "How many items should there be in the test?"
Hope this helps ....
801. best test design
saintmam February 2nd, 2009, 7:23pm:
A message from a novice.
I planify to do a survey ( about 140 questions ; the responses are the same wording 4 category with the same direction) and i would like to diminish the lenght of survey for each respondant.
I saw the anchor test design showed by M. Wolfe for equating test (Introduction to rasch measurement). The exemple show how equating and verify the quality of link for a dichotomous data.
I would like your opinion: Is it possible to do the same with a polytomous data (rating scale)? Do i have to use partial credit model? Is the same fit indice of quality of the link be use?
If not... is it better to do an common person equating?
Thank you in advance for your opinion
MikeLinacre:
Do you want to administer different items to different people, instead of all items to everyone, Saintmam? And then put all the responses into one analysis?
If so, there is no need to do any equating.
In your dataset, show the not-administered items with a special response code such as "x".
Be sure that the different subsets of items overlap, so that every item is in more than one subset.
Your items all use the same 4-category rating scale. Please use the Andrich Rating Scale model.
saintmam:
Thank you for your quick reply,
Yes i want to administer different items to different people.
What i understand is:
i could administer 140 items by 4 subset of 70 items (better test lenght) and be sure that every item is respond in 2 subsets by 80 respondants.(a total of 160 respondant)
And consider not administered items as missing data
I could do an analysis of all with Andrich rating scale model. It mean that every respondant have 50% of items as not-administered data or missing data. But i have for every item data from 80 persons.
Is it right?
I have a few more questions:
Is it a problem to have this high level of missing data ( for the reliability?)?
Do i need to do more analysis to appreciate the quality of common items?
Thank you for your help
MikeLinacre:
Your plan sounds excellent to me, Saintmam.
Every person is responding to plenty of items (70).
And every item is responded to by plenty of people (80).
The percentage of missing data (50%) is much lower than for the analysis of computer-adaptive tests and for many datasets consisting of linked tests.
My guess is that, with 80 people responding to each item, the test (sample) reliability will be about 0.8.
But if all 160 people had responded to each item, then the test reliability would be about 0.9.
Arrange your 4 test forms so that the items are as crossed as possible, then all items will become common items. Perform a DIF analysis of "item x form" to verify that items maintain their difficulty across test forms.
802. Rating scale or Partial credit
limks888 January 23rd, 2009, 8:28am:
Hi Mike,
Can you help me on this.
The ratings of 100 students on a 9-point Likert type scale to affirm the similarity between pairs of concepts (1 = most similar, 9 = least similar) is to be compared to the ratings on the same scale by an expert. Altogether there are 20 pairs of concepts to be rated.
1. Would a rating scale model or a partial credit model be more suitable for use in this case for Rasch analysis?
2. If I plan to find out the variation of the students' ratings from the expert's, what would be the type of Rasch analysis that is needed? I wish to determine the gap between the same underlying construct for the expert and the students?
Please advise.
Thank-you.
Lim
MikeLinacre:
Thank you for your questions, Lim.
1. The data design appears to be 101 raters (100 students+1 expert) by 20 pairs of concepts.
The data are too thin for PCM. Each student only has 20 observations, and each concept-item only 100 observations. Modeling the 100 students to share a rating scale, and the expert to have his own rating scale (PCM) could make sense. But the expert only makes 20 ratings. This data is much too thin to estimate a 9-point rating-scale.
So this analysis is forced to use RSM.
It is unlikely that anyone can discriminate 9 levels of similarity, so you will probably need to collapse categories together during the analysis. My guess is down to 5 categories, at most.
2. A standard Rasch analysis of the 9-category data will show the distribution of "similarity sensitivity" of the students, and place the expert within that distribution.
Suggestion: Use the expert's ratings as a scoring key,
For each student observation: 9 points if it matches the expert
8 points if it is one rating-point away
7 points if it is two away
.....
1 point if it is 8 away
Rasch analysis of these scored data will give you measures of how much the students agree with the expert.
limks888:
Thanks for your suggestion Mike.
Lim
803. Latent drift
VAYANES January 22nd, 2009, 11:33am:
We would like to know if there is any sufficient or optimal latent drift (difference between most negative and most positive item) to use a Rasch model? We apply the Rasch model to items in a Likert scale (1 - 5). Is there any relation between the latent drift and the 1-5 Likert scale?. Thank you very much.
MikeLinacre:
It seems that "latent drift" is the difference in difficulty between the easiest and the most difficult item (or easiest-to-agree-with and most-difficult-to-agree-with probe, etc.), Vayanes. This combines with the operational range of the rating scale for each item to give the overall operational range of the test/instrument.
In Rasch analysis, we prefer enough range of item difficulty to provide a clear indication of what we are measuring, as we ascend the item difficulty hierarchy (construct validity). So we expect to see a difference of more than 3 logits.
We also prefer the operational range of the instrument to be wider than the intended person sample. With a 5-category rating scale, this is not usually a problem. A 5-category rating scale probably has a range of 5 logits for each item.
So, the operational range of the test could be about 8 logits, much wider than a typical person sample.
804. Interpreting deltas and thresholds in PCM analysis
ong January 21st, 2009, 8:43pm:
Hi,
I am reading Chap 7 of Bond and Fox book on Partial Credit Model.
They explained the PCM item parameters using threshold.
I read Masters' work
Masters, G. N. (1982). A Rasch Model for Partial Credit Scoring. Psychometrika, 47(2), 149-174.
Masters, G. N. (1988). The analysis of partial credit scoring. Applied Measurement in Education, 1(4), 279-297.
When he conceptualized PCM, he discusses about step dificulites (i.e delta) but he used the term threshold to distinguish PCM with Samejina's Graded Response Model.
My questions:
(1) The output item-person map, is it refering to threshold or delta?
(2) Let say I have item 6, a 4 categories response item, how would I interpret
(i) 6.2 = 2.43 logits if it is a threshold
(ii) 6.2 = 2.43 logits if it is delta?
I am very curious, most research I read uses threshold when interpreting PCM item parameters and not delta?
Is there a special reason for that?
Regards,
Ong
MikeLinacre:
Thank you for your post, Ong. The terminology used by authors for rating-scale structures largely depends on who taught those authors. Europeans prefer Greek letters and technical terminology. Americans prefer Latin letters and non-technical terminology.
So some authors use F to indicate a Rasch-Andrich thresholds (step calibrations, step difficulties, etc.), and other authors use tau.
Some authors use D to indicate dichotomous item difficulty, some use delta.
For polytomous items, some authors use delta ij (combining the item difficulty and the threshold), others prefer Di + Fij (conceptually separating the item difficulty and the threshold).
Your question (1): We rely on authors to tell us what they are showing on their maps. There are many possibilities. But sometimes authors forget to tell us!
Your question (2) - There are many possible interpretations in different situations, but usually this means:
(i) 6.2 = 2.43 logits if it is a threshold = the location of equal probability between category 1 and category 2 is 2.43 logits above the difficulty of the item.
(ii) 6.2 = 2.43 logits if it is a delta = the location of equal probability between category 1 and category 2 is 2.43 logits above the average difficulty of all the items.
You asked: "I am very curious, most research I read uses threshold when interpreting PCM item parameters and not delta?"
Reply: Delta combines the overall difficulty of the item with the threshold between two categories. Most audiences find this confusing. They think about the overall item difficulty in the context of the meaning of the item, but they think of the thresholds between pairs of categories in the context of the response-structure. Response-structures are usually only of interest to technical audiences. Other audiences only want to know "Is this a hard or an easy item? How does it relate to other items?" They want a simple item hierarchy with no complications (i.e., they only want to know D, the item difficulty).
OK?
ong:
Thanks Mike.
You have put it in such a simple way.
Ong
805. confidence intervals in checking for invariance
ImogeneR January 21st, 2009, 3:09am:
Hi , This a little basic I suspect.
I'm trying the Ben Wright test for invariance of items where I am plotting the measures for items from top half performers (persons) in the test against the lower half and then trying to construct the CI lines around them.
I'm using the formula:
(measure_upper + measure_Lower)/2-/+SQRT (err.upper*err.upper + err.lower*err.lower)
and plotting the outcomes on inverse x and y coordinates and get nice looking confidence interval lines and my measure plot gives a nice straight line-ish plot (excpet for some wacky items in the extremes) but the top half of the items drift out of the CI lines at a different angle to the CI lines even though they are still plotted tightly on the diagonal. Is this a problem with some calculation I have made, or showing that the 'harder' items are systematically overestimated in measure for example?
Any advice much appreciated.
Imogene
MikeLinacre:
Here is probably what is happening in your data, Imogene. The bottom half of the performers (low ability) are behaving noisily (guessing, response sets, etc.) on the top half of the items (high difficulty). This means that the harder items are less (!)discriminating between high and low performers than the middle items. This can cause the drift you see in your plot.
A solution to this is to trim out responses to items that are obviously much too difficult for a performer (which is what a computer-adaptive test would do). In Winsteps, this can be done automatically with CUTLO= https://www.winsteps.com/winman/cutlo.htm
806. DIF ICCs
Raschmad January 17th, 2009, 6:09am:
Hi Mike,
In order to investigate DIF graphically, usually two ICCs for an item are drawn, each on the basis of one of the groups. If they overlap we say there's no DIF. Can we rely on Non-Uniform DIF ICC's in Winsteps Graph's menu for this purpose, even when the sample size is small (c.a.180)?
Cheers
MikeLinacre:
The reliability of DIF studies is questionable, even with large samples, Raschmad.
DIF studies have a history of reporting false positives.
Small samples can be useful for indicating if there may be a problem.
Here is one recommendation:
"When there was no DIF, type I error rates were close to 5%. Detecting moderate uniform DIF in a two-item scale required a sample size of 300 per group for adequate (>80%) power. For longer scales, a sample size of 200 was adequate. Considerably larger sample sizes were required to detect nonuniform DIF, when there were extreme floor effects or when a reduced type I error rate was required."
http://www.jclinepi.com/article/S0895-4356(08)00158-3/fulltext
807. Formatting Winsteps tables
deondb January 12th, 2009, 3:14pm:
Dear Mike
Sometime last year I read instructions on how to format Winsteps tables as more attractive tables in a wordprocessor or html. I cannot recall where I read that. Can you perhaps advise?
Regards
Deon
MikeLinacre:
Certainly, Deon. See ASCII= in Winsteps Help.
www.winsteps.com/winman/ascii.htm
deondb:
Thank you, Mike!
808. Perosn Misfit
Raschmad January 7th, 2009, 10:11am:
Hi Mike
Researchers and the literature mostly talk about the meaning and interpretation of item fit statistics and the implications of person fit and misfit are not disscussed (or probably I have overlooked it).
What does a high/low perosn infit MNSQ mean?
What does a high/low person outfit MNSQ mean?
What does a high/low perosn PTMA CORR mean?
what should be done in case of person underfit or overfit?
Thanks
MikeLinacre:
Thank you for your questions, Raschmad.
For a diagnosis of misfit, please see www.winsteps.com/winman/diagnosingmisfit.htm - and look at the Table at the bottom of that webpage.
You asked: "what should be done in case of person underfit or overfit?"
Overfit (too predictable) - usually there is no action to take. The estimated measure for the person is unlikely to be misleading, and the overfit is unlikely to distort the item measures.
Underfit (too unpredictable) - if this is only a small percentage of the sample, no action is needed. If this is a large percentage of the sample, then remedial action, such as CUTLO= and CUTHI= in Winsteps may be beneficial.
809. Item-bundle DIF for poly/dichto items
ong January 3rd, 2009, 8:38pm:
Hi,
I am interested to investigate sources of gender DIF in a mathematics test.
I am working on a dataset that consists of polytomous and dichotomous items.
I fit the data with the Partial Credit Model.
DIF is defined as the difference in the item difficulty for dichotomous items between boys and girls.
My questions:
(1) How to find DIF with polytomous items with the Rasch model? PCM?
(2) If all the items in the grometry are dichotomously scored items, does it make sense to sum the difference of the item difficulties of the ten items to flag DIF at item-bundle level--ie groups of 10 items?
(3) If the group of items in geometry consist of dichotomous and polytomous scored items, and I would like to know whether as a group of geometry items, do they function differently between gender? What should I do?
TQ
Regards,
Ong
MikeLinacre:
Thank you for your questions, Ong.
(1) How to find DIF with polytomous items with the Rasch model? PCM?
Reply: In the same way as DIF with dichotomous items. Uniform DIF is the overall difference in item difficulty of the polytomous item for boys and girls.
This is easier to conceptualize if you think of Partial Credit as Di+Fij rather than Dij where D is the difficulty, i is the item and j is the Rasch-Andrich threshold. F is the Rasch-Andrich threshold relative to the overall item difficulty, D.
(2) If all the items in the grometry are dichotomously scored items, does it make sense to sum the difference of the item difficulties of the ten items to flag DIF at item-bundle level--ie groups of 10 items?
Reply: You could do this, but it would make more sense to compute a "group DIF" common to all the items:
(Observed performance on the 10 items - Expected performance on the 10 items) ?� overall DIF effect for the 10 items
(3) If the group of items in geometry consist of dichotomous and polytomous scored items, and I would like to know whether as a group of geometry items, do they function differently between gender? What should I do?
Reply: This depends on your available software. In Winsteps, put a code in the item label for each item indicating the item's group, and then perform a Differential Group Functioning (DGF) (Table 33) for item group vs. gender.
ong:
Dear Mike,
Thank you for the responses to my qustions.
I am now using Bond & Fox Steps. The feature Differential Group Functioning (DGF) is not available in Bond&Fox Steps. I need to purchase Winsteps in oder to run DGF.
1) How to find DIF with polytomous items with the Rasch model? PCM?
Reply: In the same way as DIF with dichotomous items. Uniform DIF is the overall difference in item difficulty of the polytomous item for boys and girls.
This is easier to conceptualize if you think of Partial Credit as Di+Fij rather than Dij where D is the difficulty, i is the item and j is the Rasch-Andrich threshold. F is the Rasch-Andrich threshold relative to the overall item difficulty, D.
Referring to your response on Q1.
I revisit back my interpretation of Table 3.2.
Three items ma6, ma7 and ma 9 the output is rather interesting and perplexing.
In the original dataset, these items are scored as dichotomy. However, when I analyse them as dichotomous data, PCA Rasch residual shows high correlation. I interpret the high correlation as violation of local independence assumption.
As such, I combined the items to be polytomous scored items.
Two situations indicating the high correlation:
(1) Items where partial credit is awarded for partial response (i.e- (i) and (ii)
(2) Items sharing the same stimulus ((a, b and c)
Item ma6 consist of ma6a, ma6ai and ma6ii (partial mark for partial response and a and b sharing same stimulus)
Item 7 consist of ma7a and ma7b sharing same stimulus
Item ma9 (ma9i and ma9ii partial mark for partial response).
Let me see whether i interpret Table 3.2 correctly.
structure calibration = Rasch Andrich thresholds
structure measure = Dij
To extend the DIF concept from dichotomous to polytomous items, I will look for
Dij in table 3.2 for the separate calibration for boys and girls.
For example, item ma 6,
M F M-F
-2.29 -2.02 -0.27
0.2 -0.46 0.66
-0.5 -0.81 0.31
sum 0.7
Conclusion: On average DIF in favour of girls. However, if we will to look at individual step, step 1, the negative value shows, for step 1, DIF in favour of Male.
That means DIF might cancel off at different step. This might be a problem is the response goes different direction for different categories.
If I look at Fij = structure calibration:
M F M-F
-1.36 -0.92 -0.44
0.95 0.64 0.31
0.41 0.29 0.12
Sum -0.01
If I calculate based on Fij, it will average up to 0.
Why is there a discrepancy between the two calculation?
Did I interpret the concept correctly?
Attach here the output of Table 3.2 for the three items.
TQ.
Regards,
Ong
MikeLinacre:
Thank you for your further questions, Png.
Partial-Credit-item thresholds (and Rasch-Andrich thresholds in general) are difficult to conceptualize because they are reporting a pairwise relationship between adjacent categories. We nearly always attempt to explain this as a global relationship across all categories.
So, let's compare, the threshold between categories 0 and 1:
M = -2.29 F = -2.02
This means that for males, categories 0 and 1 are equally likely to be observed at -2.29 logits, and for females categories 0 and 1 are equally likely to be observed at -2.02 logits. So it is easier for males to score 1 than females - but only relative to 0, not relative to the other categories! For instance, it could also be more difficult for males to score 2 relative to 0 than for females to score 2 relative to 0.
This is paradoxical!
Consequently, when we want to think about overall performance on an item (as we do with DIF), it is awkward to use the Partial-Credit item parameters. It is less confusing to use global (not pairwise) values based on them. So, in your Table:
Expected
score male female
0.25 -3.46 -3.27
1 -1.43 -1.57
2 -.14 -.46
2.75 1.16 .82
This tells us that:
If we have a sample of 1,000 males, each with ability -3.46 logits, then their average score on the item will be 0.25 rating-points. 1,000 females would need a slightly higher ability, -3.27.
But, for high expected scores on the items, 2.75 rating-points, the 1,000 males would need a higher ability of 1.16 logits than the females .82.
So DIF with polytomous items is difficult to conceptualize. This is too complicated. We have difficulty explaining our findings to ourselves. Other people will not understand what we are saying.
We need to follow a basic rule of successful experimental science, "one thing at a time whenever possible"!
What does this mean for DIF?
1. Conceptualize DIF as one number, which is an overall change in item difficulty (not a pairwise change at each category threshold).
2. Model only one number to change for each gender group (the global item difficulty across all categories taken simultaneously). If we allow two things to change, they will interact and so lead to ambiguous or contradictory findings.
3. Model both genders to share the same rating scale structures. We want all the DIF gender difference, as much as possible, to be expressed by that one DIF number. We don't want it to dissipate away in different rating-scale structures (partial-credits) for different genders.
This Procrustean experimental design simplifies computation of the numbers, interpretation of the findings, and also makes communication of your findings to others much, much easier!
ong:
Thank you Mike for putting the complexities of polytomous DIF in such a simple way.
So if I will to look at polytomous DIF as an overall item diffuclty, for item ma 6a, to compute DIF it will be:
-0.93 -(-1.10) = 0.17 logits.
Girls find this item relatively easier than boys.
Another thought just cross my mind:
What if I will to look at the expected score for the overall item of to compute an index for polytomous DIF, can I use the difference of the expected score of these two groups to indicate DIF?
ES = sum k*Pink
i- item
n-person
k-category
So now i compute the expected score for boys and girls for the polytomous items
For item ma6a:
ES = {0*1 +1*exp(bn-d1) +2*exp(2bn-d1-d2) + 3*exp(3bn-d1-d2-d3)}/ sum of the numerators
The difference of the expected score indicating DIF for the item.
Questions:
(1) Does it make sense to look at polytomous DIF from overall expected score of an item?
(2) The output of Winsteps software, where can I find the information of the expected score for the overall item for different groups in separate calibrations?
(3) What should be cutoff value to signify substantial DIF? and how to test for significance?
TQ
Regards,
Ong
MikeLinacre:
This is complex, Ong.
2. If you are performing separate analyses for the two groups, then in those two analyses, the observed total score on each item will be the same as the observed expected score on each item.
1. But the expected score (and the observed score) will include both the DIF effect and the ability distribution of the group.
3. "substantial DIF" - please look at the categories of the polytomous rating scale to decide how much DIF is substantial.
"test for significance" - not sure about this, probably the easiest way is to do a simulation study to discover the joint distribution of the expected scores for the two groups.
ong:
Thanks Mike. You have enlightened me on this complex issue of polytomous DIF.
810. Two instruments, same construct?
limks888 January 5th, 2009, 2:44pm:
Hi Mike,
Can you help me on this?
I plan to design two instruments.
Instrument A (30 dichotomous items) and instrument B (30 dichotomous items) is each pilot tested on the same group of 50 studentsto obtain their scores on each of the two instruments. Instrument A and B aims to assess their conceptual knowledge of Electric circuits and Mechanics respectively. The data are then fitted to the Rasch model. Those items with infit and outfit mean square between 0.8-1.2 are retained.
The two calibrated instruments are then tested on another group of 50 students. My questions are:
1. How do we know that the two instruments are measuring the same unidimensional construct or otherwise?
2. If they do measure the same unidimensional construct of say physics ability,can I combine the two calibrated instrument items into a single instrument C? Will data from this new instrument fit the Rasch model?
Thanks,
Lim
MikeLinacre:
Thank you for your questions, Lim.
1. The question is: "Are Circuits and Mechanics part of the same overall dimension?"
An immediate check is to cross-plot the two sets of person measures. Each person has a measure on Instrument A and a measure on Instrument B. When the measures for each person are plotted with A on the x-axis and B on the y-axis, do the measures form a statistical straight line, parallel to the identity line?
If so, there is empirical evidence that the two instruments are measuring the same thing.
2. If 1 is successful, then combining the tests into a 60 item test for each person will also be successful.
| Rasch-Related Resources: Rasch Measurement YouTube Channel |
|---|
Rasch Measurement Transactions &
Rasch Measurement research papers - free |
An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse |
Rasch Measurement Theory Analysis in R, Wind, Hua |
Applying the Rasch Model in Social Sciences Using R, Lamprianou |
El modelo métrico de Rasch:
Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition),
Manuel González-Montesinos M. |
| Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar |
Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
Rasch Models for Measurement, David Andrich |
Constructing Measures, Mark Wilson |
Best Test Design - free, Wright & Stone
Rating Scale Analysis - free, Wright & Masters |
| Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias |
Diseño de Mejores Pruebas - free, Spanish Best Test Design |
A Course in Rasch Measurement Theory, Andrich, Marais |
Rasch Models in Health, Christensen, Kreiner, Mesba |
Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen |
| Rasch Books and Publications: Winsteps and Facets |
|---|
| Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene |
Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver |
Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone |
Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale |
Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland |
| Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes |
Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang |
Statistical Analyses for Language Testers (Facets), Rita Green |
Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind |
Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M |
| Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind |
Rasch Measurement: Applications, Khine |
Winsteps Tutorials - free
Facets Tutorials - free |
Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre |
Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan |
| Rasch Meta-Metres of Growth for Some Intelligence and Attainment Tests: A Meta-metre for some Intelligence and Attainment Tests, David Andrich, Ida Marais, Sonia Sappl |
|
|
|
|
| Coming Rasch-related Events |
|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
