Sample-free Test Calibration and Person Measurement
My topic is a problem in measurement. It is an old problem in
educational testing. Alfred Binet worried about it 60 years ago.
Louis Thurstone worried about it 40 years ago. The problem is still
unsolved. To some it may seem a small point. But when you consider
it carefully, I think you will find that this small point is a
matter of life and death to the science of mental measurement. The
truth is that the so-called measurements we now make in educational
testing are no damn good!
 Ever since I was old enough to argue with my pals over who had
the best IQ (I say "best" because some thought 100 was perfect and
60 was passing), I have been puzzled by mental measurement. We were
mixed up about the scale. IQ units were unlike any of those
measures of height, weight, and wealth with which we were learning
to build a science of life. Even that noble achievement, 100
percent, was ambiguous. One hundred might signify the welcome news
that we were smart. Or it might mean the test was easy. Sometimes
we prayed for easier tests to make us smarter.
Ever since I was old enough to argue with my pals over who had
the best IQ (I say "best" because some thought 100 was perfect and
60 was passing), I have been puzzled by mental measurement. We were
mixed up about the scale. IQ units were unlike any of those
measures of height, weight, and wealth with which we were learning
to build a science of life. Even that noble achievement, 100
percent, was ambiguous. One hundred might signify the welcome news
that we were smart. Or it might mean the test was easy. Sometimes
we prayed for easier tests to make us smarter.
Later I learned one way a test score could more or less be used.
If I were willing to accept as a whole the set of items making up
a standardized test, I could get a relative measure of ability. If
my performance put me at the eightieth percentile among college
men, I would know where I stood. Or would I? The same score would
also put me at the eighty-fifth percentile among college women, at
the ninetieth percentile among high school seniors, and above the
ninety-ninth percentile among high school juniors. My ability
depended not only on which items I took but on who I was and the
company I kept!
The truth is that a scientific study of changes in ability [ of
mental development ] is far beyond our feeble capacities to
make measurements. How can we possibly obtain quantitative answers
to questions like: How much does reading comprehension increase in
the first three years of school? What proportion of ability is
native and what learned? What proportion of mature ability is
achieved by each year of childhood?
I hope I am reminding you of some problems which afflict present
practice in mental measurement. The scales on which ability is
measured are uncomfortably slippery. They have no zero point and no
regular unit. Their meaning and estimated quality depend upon the
specific set of items actually standardized and the particular
ability distribution of the children who happened to appear in the
standardizing sample.
If all of a specified set of items have been tried by a child
you wish to measure, then you can obtain his percentile position
among whatever groups of children were used to standardize the
test. But how do you interpret this measure beyond the confines of
that set of items and those groups of children? Change the children
and you have a new yardstick. Change the items and you have a new
yardstick again. Each collection of items measures an ability of
its own. Each measure depends for its meaning on its own family of
test takers. How can we make objective mental measurements and
build a science of mental development when we work with rubber
yardstick?
Objectivity in Mental Measurement
The growth of science depends on the development of objective
methods for transforming observation into measurement. The physical
sciences are a good example. Their basis is the development of
methods for measuring which are specific to the measurement
intended and independent of variation in the other characteristics
of the objects measured or the measuring instruments used. When we
want a physical measurement, we seldom worry about the individual
identity of the measuring instrument. We never concern ourselves
with what objects other than the one we want to measure might
sometime be, or once have been, measured with the same instrument.
It is sufficient to know that the instrument is a member in good
standing of the class of instruments appropriate for the job.
When a man says he is at the ninetieth percentile in math
ability, we need to know in what group and on what test before we
can make any sense of his statement. But when he says he is
five feet eleven inches tall, do we ask to see his yardstick? We
know yardsticks differ in color, temperature, compositions, weight
- even size. Yet we assume they share a scale of length in a manner
sufficiently independent of these secondary characteristics to give
a measurement of five feet eleven inches objective meaning. We
expect that another man of the same height will measure about the
same five feet eleven even on a different yardstick. I may be at a
different ability percentile in every group I compare myself with.
But I am the same 175 pounds in all of them.
Let us call measurement that possesses this property "objective"
(2, 4, 5). Two conditions are necessary to achieve it. First, the
calibration of measuring instruments must be independent of those
objects that happen to be used for calibration. Second, the
measurement of objects must be independent of the instrument that
happens to be used for measuring. [There is a third condition which
follows from the first two. The evaluation of how well a given set
of observations can he transformed into objective measurements must
be independent of the objects and instruments that are used to
produce the observations. It must also be reasonable to hypothesize
that objects and instruments have stable characteristics which do
not interact with each other.] In practice, these conditions can
only be approximated. But their approximation is what makes
measurement objective.
Object-free instrument calibration and instrument-free object
measurement are the conditions which make it possible to generalize
measurement beyond the particular instrument used, to compare
objects measured on similar but not identical instruments, and to
combine or partition instruments to suit new measurement
requirements. [Were it useful to glue three 12-inch rulers together
to make a 36-inch yardstick or to saw a 36-inch yardstick in three
to make some 12-inch rulers. we would retain our confidence in the
objective meaning of length measurements made with the resulting
new instruments.]
The guiding star toward which models for mental measurement
should aim is this kind of objectivity. Otherwise how can we ever
achieve a quantitative grasp of mental abilities or ever construct
a science of mental development? The calibration of test-item
easiness must be independent of the particular persons used for the
calibration. The measurement of person ability must be independent
of the particular test items used for measuring.
When we compare one item with another in order to calibrate a
test, it should not matter whose responses to these items we use
for the comparison. Our method for test calibration should give us
the same results regardless of whom we try the test on. This
is the only way we will ever be able to construct tests which have
uniform meaning regardless of whom we choose to measure with
them.
When we expose persons to a selection of test items in order to
measure their ability, it should not matter which selection of
items we use or which items they complete. We should be able to
compare persons, to arrive at statistically equivalent measurements
of ability, whatever selection of items happens to have been used
- even when they have been measured with entirely different
tests.
An Individualistic Approach to Item Analysis
Exhortations about objectivity and sarcasm at the expense of
present practices are well and good. So what? Can anything be done
about it? Is there a better way?
In the old way of doing things, we calibrate a test item by
observing how many persons in a standard sample succeed on that
item. Item easiness is defined by the proportion of correct
responses in the sample [p-value]. Item quality is estimated from the
correlation between item response and test score [point-biserial correlation]. Person ability is
defined by percentile standing in the sample. This approach leans
heavily on assumptions concerning the appropriateness of the
standardizing sample of persons.
A different approach is possible, one in which no assumptions
need be made about the persons used. This new approach assumes
instead a very simple model for what happens when any person
encounters any item. The model says simply that the outcome of the
encounter is governed by the product of the ability of the person
and the easiness of the item. Nothing more. The more able the
person, the better his chances for success with any item. The
easier the item, the more likely any person is to solve it. It is
as simple as that.
But this simple model has a surprising consequence for item
analysis. When measurement is governed by this model, it is
possible to take into account whatever abilities the persons in the
calibration sample happen to have and to free the estimation of
item easiness from the particulars of these abilities. The scores
persons obtain on the test can be used to remove the influence of
their abilities from the item analysis. The result is a person-free
test calibration.
I learned this kind of item analysis from the Danish
mathematician Georg Rasch. But comparable work has been done here
by Frederic Lord and Allan Birnbaum. Some of the ideas have been in
print for years. What is surprising is that this powerful
method is not used in practice.
Why not? Perhaps too few recognize the importance of objectivity
in mental measurement. Perhaps, too, many despair that it can ever
be achieved, or fear it will be too difficult to do. What we need
is some evidence that objective measurements of mental ability can
really be made.
The crucial questions are: Can test calibration really be
independent of the ability characteristics of the persons used to
make the calibration? Can person measurement, the estimation of a
person's ability from a score on some selection of test items,
really be independent of those items used for the measurement?
The data in this paper illustrate that both of these ideals can
be lived up to in practice. These data happen to come from the
responses of 976 beginning law students to 48 reading comprehension
items on the Law School Admission Test. But they are only one
illustration. The method has also worked with other mental tests
(2).
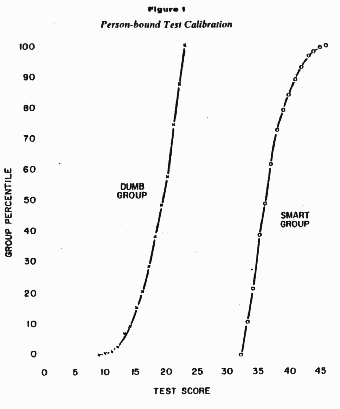
Person-free Test Calibration
In order to examine the dependence of test calibration on the
abilities of these law students, let us construct the worst
possible situation. Into a Dumb Group we will put the 325 students
who did worst on the test. The best of them got a score of 23. Into
a Smart Group we will put the 303 students who did best. The worst
of them got a score of 33. Thus, we have two groups dramatically
different in their ability to succeed on this test of reading
comprehension. There are 10 points difference between the smartest
of the Dumb Group and the dumbest of the Smart Group.
Now for the acid test. How would a test calibration based on the
Dumb Group compare with one based on the Smart Group? To remind us
of how things look using the old way of doing things, I made up
these calibrations in terms of sample percentiles. Each curve in
Figure 1 represents a person-bound test calibration. The curve on
the left is the test calibration produced by the Dumb Group. The
curve on the right is the test calibration produced by the Smart
Group.
Obviously any person-bound calibration based on the Dumb Group
is going to be incomparable with one based on the Smart Group. From
the Dumb Group we can only set up percentile ability measures for
students who score between 10 and 23. From the Smart Group we can
only set them up for students who score between 33 and 46. These
two calibrations do not even overlap. And what about all the
scores outside the range covered by either group?
Of course Figure 1 describes an exaggerated situation. No one in
his right mind would attempt to base a test calibration on two such
different groups. But this exaggeration has a purpose. It is aimed
at bringing out a treacherous property of person-bound test
calibration and providing an acid test for any method which claims
to be person-free.
Now let us see how well the new way of test calibration handles
this exaggerated situation. I will not burden you with mathematical
details. They are covered in the references. (Should you
become interested in applying the method let me know. I have a
dandy computer program which does it nicely.) Let us look at the
results.
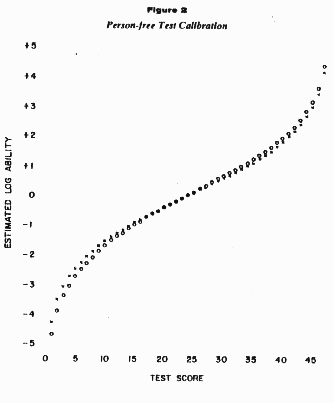
Figure 2 is based on the same data, same test, same students,
and the same two calibration curves. But a different method of
calibration. As in Figure 1, the x's mark the test calibration
based on the Dumb Group. The o's mark the calibration based on the
Smart Group. But now, in Figure 2, how different are the two
calibration curves?
At this point you may have a question about how calibration
curves work to turn test scores into ability measurements.
Each curve represents a conversion table. When a person gets a
score on the test, you enter the graph at that score along the
bottom, look up vertically to a calibration curve, and then across
to the left horizontally to read off his ability. In Figure 2,
ability is expressed in logs. If you do not like logs, you can take
the anti-loge and get an ability measure on a ratio scale. This may
interest you because then ability is measured on a scale where zero
means exactly no ability and for which a regular and meaningful
unit can be defined. [For a score of 15, the estimated loge ability
is about -1.0 and the ratio scale ability is about 0.4. A score of
33 indicate a loge ability of about + 1.0 and a ratio scale ability
of about 2.7. Thus, a score of 35 indicates about 7 times more
ability than a score of 15.]
In Figure 1, the calibration curves do not even come close to
each other. In Figure 2 they are almost indistinguishable. [There
is a slight systematic difference. But this reading comprehension
test was taken as it stood without any modifications in favor of
fitting the item-analysis model. When test items are chosen to
conform to the statistical requirements of the model, then no
systematic differences between calibrations are discernible.] Would
you say that the difference between the two calibrations in Figure
2 was of practical significance? How much would you care which of
these calibration curves you used to make the test a measuring
instrument for you? And yet the two groups on which they are based
were constructed to make it as hard as possible to achieve person-
free test calibration.
One thing that may puzzle you about Figure 2 is the range of
test calibration. Either calibration curve provides ability
measures for all raw scores on the test from 1 to 47. How can that
be done when neither group obtained more than a few of the scores
possible?
The answer lies in the item-analysis model on which these
calibration curves are based. Remember that this model uses no
assumptions about the abilities of the calibration sample. Its only
assumption is what happens when any person encounters any item. Out
of this assumption it is possible to calibrate a test over its
entire range of possible scores even when everyone in the
calibration sample happens to get the same score.
That sounds impossible. But it follows directly from this new
item-analysis model. The important idea is that even with the same
total score, persons differ in those items on which they succeed.
When the calibration sample is large, these differences can be used
to calibrate the items, and, hence, the test over its entire range
of possible scores, even though only one score has actually
been observed.
Comparing the calibrations shown in Figures 1 and 2, then, we
can see the contrast between the present way of doing things -
calibration based on the ability distribution of a standardizing
sample - and a new way of doing things - calibration that is free
from the effects of the ability distribution of the persons used
for the calibration. Which do you prefer?
[Even if you use this new way as your basis for calibration, you
can still construct all the percentile standardizations you want.
Nothing will prevent you from embedding your ability measures in as
many sample contexts as you like. But, and this is the vital point,
you will not be bound by those contexts. You will have an ability
measure which is invariant with respect to the peculiarities of the
persons used to establish the test calibration. If you were a test
manufacturer, you would not have to worry about whether you had
obtained the right standardizing samples to suit your customers.
Your test would be equally valid for all situations in which the
test was appropriate. At the same time, since the calibration was
person-free, you would he able to use new data as they came in, to
verify and improve item calibration, to add to the item pool, and
to document the scope of situations in which the test was
functioning properly.]
Item-free Person Measurement
So much for person-free test calibration. Now, how about the
companion question? Can ability be measured in a fashion that frees
it from dependence on the use of a fixed set of items? Is item-free
person measurement possible? If a pool of test items has been
calibrated on a common scale, can we use any selection we want from
that pool to make statistically equivalent ability
measurements?
In order to judge whether person measurement can be independent
of item selection, we want a situation that will make it as
difficult as possible for person measurement to be item-free. For
this we will divide the 48 items on the original test into two
subtests of 24 items each with no items in common between them.
It would be tempting to make these subtests equal in overall
easiness. Then they would be parallel forms. But that would be too
tame to challenge a scheme for item-free person measurement.
Instead, the two subtests will be made as different as possible.
The 24 easiest items will be used to make an Easy Test. The 24
hardest items will be used to make a Hard Test. Now, under these
circumstances, what is the evidence that ability measurement can be
item-free? In other words, what is the evidence that the ability
estimates based on the Easy Test are statistically equivalent to
those based on the Hard Test?
Why do I say statistically equivalent? We know that there are a
wide variety of factors at work when a person takes a test. Even
knowing a person's ability and an item's easiness will not tell us
exactly how he will do on the item. At most we can say what his
chances are. This uncertainty follows through into his test score.
Even if we could give a person the same test twice, wiping all
memory of the first exposure from his mind before his second trial,
we would not expect him to get the same score both times. We know
there will be some variation. This uncertainty is an inevitable
part of the situation. It is the error of measurement.
In finding out just how item-free person measurement can be, we
must make allowance for this uncertainty. There is no point in
asking whether estimates of ability based on the Easy Test are
identical with those based on the Hard Test. We know they cannot
be. But we can ask whether the two estimates are close enough so
that their differences are about what we expect from the
uncertainties in the testing situation. Are they close enough in
the light of their error of measurement to be considered
statistically equivalent?
To answer this question we will examine the test responses of
the 976 law students to the 48-item test. The score each student
earned on the whole test can be split into a subscore on the Easy
Test and a subscore on the Hard Test. This gives each student a
pair of independent scores each of which should provide an
independent estimate of his reading comprehension ability. In order
to convert these scores into ability measures on a common scale, we
will calculate calibration curves like the one in Figure 2 for each
of the subtests. To do this, we will use item calibrations on a
scale common to all 48 items. Then the separate calibration curves
for the Easy and Hard tests will convert scores on these different
tests into ability estimates on a common scale. If the data fit the
item-analysis model, then the independent results from these two
different rests should produce statistically equivalent ability
estimates.
| Table 1 |
|---|
| Item-free Person Measurement |
|---|
| Test Score |
|---|
| | Easy
Test | Hard
Test | Difference | |
| Mean | 17.16 | 10.38 | 6.78 |
| Std. Error | 0.13 | 0.14 | 0.11 |
| Std. Deviation | 3.93 | 4.29 | 3.30 |
|
|
| Estimated Loge Ability |
|---|
| | Easy
Test | Hard
Test | Difference | Standardized
Difference |
| Mean | .464 | .403 | .061 | 0.003 |
| Std. Error | .032 | .028 | .024 | 0.032 |
| Std. Deviation | .997 | .868 | .749 | 1.014 |
| Std. Error | | | | 0.023 |
The data are in. The upper half of the table is an
obvious example of item-bound person measurement. The 976 law
students average 6.78 points more on the Easy Test than they do on
the Hard one. This problem has been handled in the past by
referring such test scores back through a percentile table based on
some well-chosen standardizing sample of students who have taken
both forms [equipercentile equating]. That is one way to equate two tests which are supposed
to measure the same ability. The trouble is that this equation
depends on the characteristics of the sample of persons used
to equate the tests. We know that an equation based on one group of
persons is not, in general, appropriate for equating measurements
made on persons from another group.
Is there a better way to equate tests? Can we go directly from
a test score and a person-free calibration of the test items to a
measure of ability which does not lean on any particular
standardizing sample and which is statistically invariant with
respect to those of the calibrated items that are actually used to
obtain the score?
The lower half of Table 1 shows how the new approach equates the
Easy and Hard tests. We have each person's score on the Easy Test
and his score on the Hard Test. For each score we look up the
corresponding estimated loge ability on calibration curves like the
ones in Figure 2. For each pair of scores we obtain a pair of
estimated loge abilities. They will not be identical. But how do
they compare statistically?
The distribution of score differences with a mean of 6.78 and a
standard deviation of 3.30 is almost entirely above zero. But the
distribution of ability differences with a mean of .061 and a
standard deviation of .749 is nicely situated right around
zero. On the average, these alternative estimates of ability seem
to be aiming at the same thing.
How does the variation around zero compare with what would be
expected from errors of measurement alone? To examine this, we will
standardize the differences in ability estimates. For each test
score there is not only its corresponding ability estimate but also
the measurement error that goes with that ability estimate. The
difference between the easy Test and Hard Test ability estimates
can be divided by the measurement error of this difference to
produce a standardized difference.
It is the distribution of these standardized differences that
will show us whether or not the two ability estimates are
statistically equivalent. If they are, then this standardized
variable should have a mean of zero and a standard deviation of
one. That would mean that the only variation observed in ability
estimates was of the same magnitude as that expected from the error
of measurement in the test. Table 1 shows that for these 976
students, the standardized differences in ability estimates between
the Easy and the Hard tests have a mean of 0.003 and a standard
deviation of 1.014. Is that close enough to zero and one?
What does item-free person measurement mean for test
constructors and test users? If you can make statistically
equivalent person measurements from any selection of items you
wish, then all the tricky and difficult problems of equating
parallel forms, connecting sequential forms, and relating short and
long forms disappear. Incomplete data ceases to be a problem. You
can measure a person with whatever items he answers.
Once you have developed a pool of items that conforms to this
item-analysis model and once you have calibrated these items, then
you are free to make up any tests you wish out of any selection
from this item pool. On the basis of these item calibrations alone
and without any further recourse to standardizing samples, you can
compute a calibration curve or a table of estimated abilities along
with their errors of measurement for every possible score on any
subtest you want to construct.
All such abilities will be on the same ability scale whatever
subset of items they were estimated from. You can measure John on
an Easy Test and Jim on a Hard Test and be able to compare their
resulting estimated abilities on the same ratio scale. That means
you can say how many times more or less able John is than Jim in a
precise, quantitative way
You can measure many children with a short test and a few with
a longer, more precise test and still put all the measures on
the same ability scale. Think of how this would expedite screening
and selection procedures. The number of items you give a child
could depend on how close he comes to the point of decision.
Children far away on either side would be quickly detected with a
few items. Only children very near the decision point would require
longer tests in order to estimate more precisely on which side of
the criterion their ability lies.
In general, you would let the required precision, the acceptable
error of measurement, determine test length. You would not be bound
to any particular predetermined set of items. You could select
items from a calibrated pool and compose test forms
extemporaneously to suit your measurement needs. [The most
important criterion for item selection is the magnitude of
measurement error. This is minimum when the person being measured
has even odds to succeed on the item. That means that we would like
to choose items that are just right for the person being measured,
items just as easy as the person is able. In individual or
computerized testing, where it is possible to choose the next item
on the basis of information gathered from the person's performance
up to that point, this rule specifies exactly what item to use
next.]
Yet all the measurements made with selections of items from this
pool would be located on one scale and used to define whatever
norms you or your friends desire. Indeed, since item analyses would
be both person- and item-free, it would be easy to construct tests
so that all new data which came in could be used directly to verify
and improve item calibration, to add new items to the item pool, to
document the range of persons with whom the test was functioning
satisfactorily, and to establish and extend ability norms for
whatever groups were being tested.
The Item-analysis Model for Measuring Ability Objectively
By now I hope I have whetted your appetite to know more about
the item-analysis model which made these person-free test
calibrations and item-free person measurements possible. The
measuring model contains just two parameters. One of these belongs
to the person and represents the amount of his ability, Zn. The
other belongs to the item and represents the degree of item
easiness, Ei. The model combines these two parameters to make a
probabilistic statement about what happens when the person tries
the item.
Here is the measuring model: The odds in favor of success, Oni,
are given by the product of the person's ability, Zn, and the
item's easiness, Ei.
Oni = ZnEi
[This can equally well be expressed in terms of loge odds Lni,
loge ability Xn, and loge easiness Di as
Lni = loge Oni = Loge Zn + Loge Ei = Xn + Di
The loge odds form brings out the simple linear structure from
which this model derives its optimal measuring properties.]
This is the same as saying that: The probability Pni that a
person with ability Zn will succeed on an item with easiness Ei is
the product ZnEi. of his ability and the item's easiness divided by
one plus this product.
Pni = ZnEi/( 1 + ZnEi )
[This can equally well be expressed in terms of the logistic
function as
Pni = 1/(1 + exp ( - (Xn + Di)) ).
]
This is the measuring model used to analyze the 48 reading
comprehension items on the Law School Admission Test.
What does this simple model say about the scale on which person
ability and item easiness are measured? Odds vary from zero to
infinity. Since this model gives the odds in favor of success as
the product of person ability and item easiness, the natural scale
on which to define ability and easiness is one that also varies
between zero and infinity
What does that mean? When a person has no ability, his zero
ability will give him zero odds in favor of success no matter what
item he tries. With no ability he has no chance of succeeding. On
the other hand, if an item has no easiness, then it is infinitely
hard and no one can solve it. Measurements made on these scales of
ability and easiness have a natural zero.
What about the unit of measurement? Reconsider the product of
person ability and item easiness, ZnEi. There is an indeterminacy
in that product. We can multiply ability by any factor we like and
not change the product, as long as we divide easiness by the same
factor. This shows us that if we want to make measurements, we will
have to define a measurement unit.
How can such a unit be defined? One way is to select a special
group of items as standard. These items can be chosen on
theoretical or normative grounds. They can be chosen because they
represent a minimal or optimal level of ability. Once chosen, the
combined easiness of these items is set at one. This calibration
will then define a person's ability as his odds for success on
these standard items.
When a person is functioning at about the level of easiness of
these items, then his ability is about one. If he is below the
level of these items, then his ability is less than one. If, in the
course of development or education, he doubles his odds for
success, that will mean he has doubled his measured ability. Thus,
one way a unit of measurement can be defined is in terms of even
odds to succeed on items selected to be standard. The unit of
measurement becomes even odds on the standard items.
Another way to define a unit of measurement is in terms of
standard persons. These persons can be chosen because they are
typical, because they are liminal for some criterion, or because
they are the dumbest persons you can find. Now the ability unit is
the ability of these standard persons. If you are just at their
standard, your ability is one. If your odds to succeed on any item
are twice those of a standard person, your ability is two.
In our exploration of what zero means and how to define a unit
of measurement, we have uncovered the sense in which measures made
with this item-analysis model are on a ratio scale. When one item
is twice as easy as another then any person's odds for success on
the easier item are twice his odds for success on the harder one.
When one person is twice as able as another, then his odds for
success on any item are twice those of the less able person.
Finally, and most important, this simple item-analysis model has
a mathematical property that is vital to objectivity in mental
measurement. When observations are made in terms of dichotomies
like right/wrong, success/failure, it is a mathematical fact that
this is the only model that leads both to person-free test
calibration and to item-free person measurement. When observations
are dichotomous, the simple form of this item-analysis model is the
sufficient and necessary condition for objective mental
measurement.
Test Construction and the Future of Item Analysis
What bearing does this model for measuring ability objectively
have on the construction of mental tests? The model is so simple
that those of you who have worried about how to do item analysis
may ask: "What about guessing? What about item discrimination? What
about the influence of one test item on another?"
It is obvious that in any real testing situation all of these
factors play some part. But I prefer to ask: "What do we want to do
with them? How big a part do we want guessing, discrimination, and
inter-item dependence to play in our measuring instruments?"
We can construct tests in which guessing plays a big part, in
which items vary widely in their discrimination, and in which the
answer to one item prepares for the next. But do we want to? Not if
we aspire to objective mental measurements. If we value
objectivity, we must employ our test-conducting ingenuity in the
opposite direction.
Most item-analysis models use at least two parameters to
describe items. In addition to item easiness, which is part of the
simple model presented here, there is also item discrimination.
This represents the item's power to magnify or attenuate the extent
to which ability is expressed. The discovery of item discrimination
was an important step toward understanding how items behave. But as
a parameter in the final measuring model it is fatal to
objectivity.
If item discrimination is allowed to remain as an active
parameter in the measuring model, if gross variation in item
discrimination is tolerated in the final pool of test items, then
the possibility of person-free test calibration is lost. [It may be
useful to estimate item discrimination when constructing an item
pool in order to bring it under control through item selection. But
there are more general statistical tests for whether an item or a
set of items fits this simple item-analysis model. Probably these
more general tests will turn out to be more generally useful.]
What does this mean for test construction? If we use multiple-
choice items, we will devise distractors that make guessing
infrequent. When we conduct a pilot study of the characteristics of
potential items, we will select items for the final pool that
discriminate equally and fit an objective measuring model.
You might complain that this nice advice is impossible to
follow. Do not despair. The reading comprehension items on the Law
School Admission Test were not constructed for equal discrimination
or item independence. They are multiple-choice items with five
alternatives. They differ considerably in discrimination, and they
are grouped around common paragraphs of text to be read for
comprehension. Yet without guessing, without discrimination, and
assuming item independence, the simple item-analysis model
succeeded quite well, even with these unfit data.
This shows that the measuring model stands up even when one
departs from its assumptions. We do not have to create a
perfect test in order to use the model. That does not mean no
further thought need be given to test construction. If we care
about building a science of mental development, then we must be
interested in objective mental measurement. If we are interested in
objective mental measurement, then the ideals of no guessing, equal
discrimination, and item independence can guide us toward
constructing better tests. And the kind of item analysis I have
illustrated can transform observations made with these tests into
objective mental measurements.
How far have we progressed in the science of mental development
since the work of Alfred Binet 60 years ago? I am talking about
science and not the overwhelming expansion in organization and
technique to which our massed presence at this conference
testifies. Have you ever wondered why progress is so slow?
Something must be wrong. I believe progress will continue to be
slow until we find a way to work with measurements which are
objective, measurements which remain a property of the person
measured regardless of the test items he answers or the company he
keeps.
1. Loevinger, J. Person and population as psychometric concepts.
Psychological Review, 1965, 72, 143-155.
2. Rasch, G. Probabilistic Models for Some Intelligence and
Attainment Tests. Copenhagen: Danish Institute for Educational
Research. 1960. Chapters V-VII, X.
3. Rasch, G. On general laws and the meaning of measurement in
psychology. In Proceedings of the Fourth Berkeley Symposium on
Mathematical Statistics. Berkeley: University of California Press,
1961, IV, 321-334.
4. Rasch, G. An individualistic approach to item analysis. In
Readings in mathematical social science. Edited by Lazarsfeld and
Henry. Chicago: Science Research Associates Inc., 1966. Pp. 89-
107.
5. Rasch, G. An item analysis which takes individual differences
into account. British Journal of Mathematical and Statistical
Psychology. 1966, 19, Part 1, 49-57.
6. Sitgreaves, R. Review of probabilistic models for some
intelligence and attainment tests. Psychometrika, 1963, 28, 219-
220.
 Ever since I was old enough to argue with my pals over who had
the best IQ (I say "best" because some thought 100 was perfect and
60 was passing), I have been puzzled by mental measurement. We were
mixed up about the scale. IQ units were unlike any of those
measures of height, weight, and wealth with which we were learning
to build a science of life. Even that noble achievement, 100
percent, was ambiguous. One hundred might signify the welcome news
that we were smart. Or it might mean the test was easy. Sometimes
we prayed for easier tests to make us smarter.
Ever since I was old enough to argue with my pals over who had
the best IQ (I say "best" because some thought 100 was perfect and
60 was passing), I have been puzzled by mental measurement. We were
mixed up about the scale. IQ units were unlike any of those
measures of height, weight, and wealth with which we were learning
to build a science of life. Even that noble achievement, 100
percent, was ambiguous. One hundred might signify the welcome news
that we were smart. Or it might mean the test was easy. Sometimes
we prayed for easier tests to make us smarter.