Richard Perline, University of Chicago
Benjamin D. Wright, University of Chicago
Howard Wainer, Bureau of Social Science Research
The object of this paper is to present Rasch's psychometric model as a special case of additive conjoint measurement. The connection between these two areas has been discussed before, but largely ignored. Because the theory of conjoint measurement has been formulated deterministically, there have been some difficulties in its application. It is pointed out in this paper that the Rasch model, which is a stochastic model, does not suffer from this fault. The exposition centers on the analyses of two data sets, each of which was analyzed using Rasch scaling methods as well as some of the methods of conjoint measurement. The results, using the different procedures, are compared.
Although conjoint measurement is generally acknowledged as an important theoretical contribution, its practicality has been questioned. Apparently not many psychologists are aware that the Rasch (1960) model is a practical realization of conjoint measurement, and the literature contains only a few references (Brogden, 1977; Fischer, 1968; Keats, 1967, 1971) to the connection between these two models. (Tversky (1967) discussed the Bradley-Terry-Luce choice model, which is closely related to the Rasch model, in terms of conjoint measurement. Young (1972) also considered the Bradley-Terry-Luce model in these terms and remarked generally that "the scaling methods in psychometrics conform to the notion of polynomial conjoint measurement.")
It is surprising that this connection has been ignored, particularly in view of the complaints made about the problems of applying conjoint measurement to real data:
In their current status, the fundamental measurement theories are algebraic, that is, deterministic. Their predictions do not lend themselves easily to empirical verification. Any departure of the data from the theory amounts to a puzzle to which the standard decision rules of statistics do not apply. (Falmagne, 1976)
Similarly, Cliff (1973) mentioned "the relative failure of axiomatic measurement theory to handle the difficulties posed by the inconsistencies inherent in fallible data." He went on to say that what would most convince psychologists of the value of these concepts is "one really striking empirical example in which the axiomatic measurement theory approach led to a marked simplification of an area or to an important new substantive insight."
The Rasch model is an example of conjoint measurement with an underlying stochastic structure. As a stochastic model, it can be applied to empirical data and tested for goodness-of-fit using the general procedures of statistical inference, not just the rule-of-thumb guidelines or the monte carlo methods which characterize the evaluation of the algebraic conjoint measurement models. In response to Cliffs plea for a "striking empirical example," the Rasch model provides the possibility of demonstrating measurement objectivity of a sort not previously thought possible in psychometrics. Rasch (1966) has coined the term "specific objectivity" to describe the particular characteristic of his model which permits the comparison of two subjects independent of which instruments (stimuli) are used to measure them, as well as the comparison of two instruments independent of the subjects on whom they are used. In short, the Rasch model is a practical example of how conjoint measurement can be applied to empirical data.
The purpose of this paper is to illustrate the connection between the Rasch model and conjoint measurement with the analyses of two sets of data, each of which was first analyzed using Rasch scaling and then using some techniques of algebraic conjoint measurement.
Conjoint Measurement and the Rasch Model
The Need for Conjoint Measurement
The theory of conjoint measurement was motivated by the realization that the theory of physical measurement was too simple to be applied in psychological research. Physical science deals with objects which admit to combining operations. It is easy to show that the weight of two lumps of clay joined into one is equal to the sum of the weights of the individual lumps. Weight is considered as a measurement system based on an empirical combining (concatenating) operation. Such a system allows more than just the comparison between single objects: It is possible to compare x concatenated with y to the object z.
While not all physical properties admit to concatenation (temperature does not), there are several that do, and these form a fundamental basis from which other forms of measurement are derived. Unfortunately, it does not seem that the attributes of interest to psychologists can be concatenated. From this it was formerly argued that the measurement of psychological properties cannot do better than ordinal scales.
Research in measurement theory, however, has led to a different conclusion. It is now known that an empirical concatenation operation is not necessary for interval scale measurement, and several models have been proposed which yield interval scales (Coombs, Dawes, & Tversky, 1970). Additive conjoint measurement is one such model.
Conjoint measurement is concerned with the way the ordering of a dependent variable varies with the joint effect of two or more independent variables. The situation can be compared to ordinary analysis of variance where the two (or more) independent variables (factors) form a completely crossed factorial design. ANOVA tests whether the dependent variable can be represented as the sum of row and column effects. In the case of additive conjoint measurement, the question is whether or not there exists a monotonic transformation of an ordinal measure of the dependent variable from which an additive representation can be constructed. In effect, can interaction be removed by a monotonic rescaling of the dependent variable?
The axiomatization of conjoint measurement (Luce & Tukey, 1964) is more complicated than the simplified scheme given here and includes technical axioms which can often plausibly be assumed to hold approximately. When the axioms hold, the result is that the observed but transformed dependent variable and the concomitantly constructed independent variables are simultaneously (hence, the term "conjoint") represented on an interval scale with a common unit. An additive representation is achieved without the existence of an empirical concatenation operation.
The Rasch Model
To consider the Rasch model in these terms, let a sample of individuals take a mental test, and assume the probability, pij, that person i correctly responds to item j depends only on a parameter, ai, representing his/her ability and another parameter, bj, representing the easiness ("item facility") of the item attempted. Assume further that for some monotone transformation, M,
![]()
for all i and j. That is, an additive representation is postulated for the suitably transformed probabilities, pij.
Conjoint measurement theory makes no specification as to what the monotonic transformation, M, should be. Two possibilities, both of which have been considered in psychometric theory (Lord & Novick, 1968), are the inverse normal and inverse logistic transformations. The former is the special case of Lord's normal-ogive test model where item discriminations are equal. When M is the inverse logistic transformation,

(ln is the natural logarithm), we have Rasch's psychometric model.
Both models, where M is either the inverse normal or the inverse logistic, are additive in the person ability and item facility parameters. However, the Rasch model has certain very desirable statistical properties which allow for practical application in the estimation of these parameters.
Obviously, the pij are unobservable, as are the ability and item parameters. Estimates of the pij (and, hence, the ai and bj could be obtained if it were possible to give a person the same item on repeated occasions, and his/her responses were independent over trials. Clearly, this is not possible.
Alternatively, the probabilities could be estimated if people of like ability could be identified. Assuming a group of people with the same ability, since individuals respond to items independently, the observed proportion of individuals within the group who correctly respond to item j is an estimate of the probability that any given person from that group passes the item. With the Rasch model this grouping method can actually be approximated in order to estimate parameters.
Specifically, it can be shown (Lord & Novick, 1968, p. 429) that a person's raw score (number of items correct) is a minimal sufficient statistic for his/her ability. This leads to a practical implementation of the model in that statistical estimates of abilities and item parameters can be obtained by proceeding as if everyone with the same raw score has exactly the same ability.
The parameter estimates are commonly computed using an estimation method known as unconditional maximum likelihood (UCON, JMLE, Wright & Douglas, 1977; Wright & Panchapakesan, 1969). Haberman (1977) has shown that these estimates converge in probability to the true parameters, provided the number of items and the number of people grow indefinitely large at a certain rate relative to each other and provided certain other technical assumptions hold. The theoretically ideal estimation method, conditional maximum likelihood CMLE, yields consistent estimates of item parameters (Andersen, 1973), but involves computational difficulties which make it impractical for applications with large numbers of test items (Wright & Douglas, 1977).
Another method of estimation, useful for purposes of illustration here, is unweighted least squares. It begins with a data matrix of raw group by items with cell entries, Pij, the observed proportions of people with score i who pass item j. The cell entries are transformed by Equation 2 (if Pij=0 or 1 for some i and j, there is a problem, but this can be handled as in the Wright and Panchapakesan article), and then score group and item "effects" are calculated as in ANOVA. Note that here the index i refers to a score group, whereas above it was used to identify an individual; note also the difference between the observed proportions, Pij, and the theoretical probabilities, pij.
The unweighted least squares procedure can be employed for the general algebraic conjoint measurement model, except that the monotonic transformation to be used on the nij is not specified a priori. The analysis includes a searching algorithm which attempts to find the monotonic transformation that best produces additivity according to some criterion of fit. It should be emphasized, however, that raw score grouping relies on statistical theory, not conjoint measurement theory, for justification; and furthermore, it is only justified in the case of the Rasch model, which is the unique example where raw score is a minimal sufficient statistic for ability (Andersen, 1977). It should also be made clear that even if it is assumed that the Rasch model holds, the observed score group by item data matrix need not yield an exact (i.e., perfect) additive representation, since it involves observed estimates of probabilities, not the probabilities themselves.
When the items and people are scaled using algebraic conjoint measurement, there is a problem of evaluating the goodness-of-fit. With the exception of some recent work (Falmagne, 1976), there has been little attempt at developing a probabilistic framework for testing the fit using statistical inference. Nevertheless, there are empirical checks which can be used to index the quality of the fit, and although they do not provide probability statements, it is of interest to compare these with the statistical tests of the Rasch model.
Goodness-of-fit Tests in Conjoint Measurement
There are several reasonable criteria that might be used to examine goodness-of-fit of an additive model with fallible data. One natural approach has been given by Kruskal (1964) and is used in his computer program MONANOVA (Kruskal & Carmone, 1969). (See McClelland and Coombs (1975) for an alternative method.) This program uses an algorithm which searches for the monotonic transformation that best yields additivity in a factorial design. The criterion for optimizing additivity is to select the monotonic function of minimum stress. Stress is defined as follows:
Let {dij} be the data values for the factorial design (in the example, dij = fry). If M is any ascending monotonic transformation, an ordinary ANOVA can be performed on the set of transformed data values {M(dij)} and the main effects {ai} and {bj} can be obtained. From the main effects are obtained the fitted values M'(dijM) = ai + bj. The quantity sumijSum[M(dij)-M'(dij)]2 will approach 0 as M approaches additivity; its value can be scaled between 0 and 1 by dividing by sumijsumM2(dij). Taking the square root gives
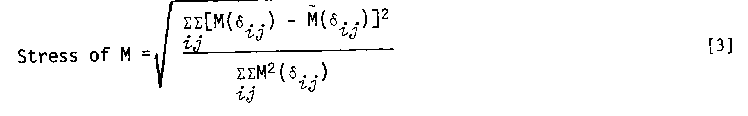
which is usually given as a percentage.
The actual search procedure used for finding the M of minimum stress involves an iterative algorithm. M is found in the discrete sense (i.e., numerically) and is unique only up to a positive linear transformation. The output of MONANOVA includes a plotted graph of the data points {dij} vs. their transformed values {M(dij)}; also given are the main effects, which in the example correspond to the ability estimates for each raw score and the item facilities. The stress value computed for the optimal M is an index of how well additivity has been achieved.
(A data matrix is said to be additive if it can be monotonically rescaled such that each rescaled value is equal to the sum of its row and column components.) Another approach to testing for additivity, which is nonconstructive in the sense that no function M is found, is to examine the data with respect to two ordinal properties that are necessary conditions for additivity (Krantz, Luce, Suppes, & Tversky, 1971). The first of these is the monotonicity (or independence) condition which asserts that a data matrix is additive only if its rows and columns can be permuted to make its elements monotonically increasing from left to right and from top to bottom. That is, the rows and columns of an additive MxN data matrix (dij) can be rearranged to form the matrix (d'ij) with the property that
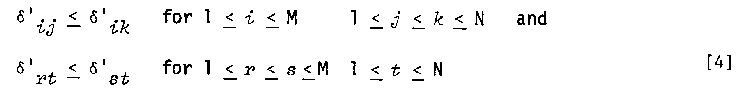
As an empirical check on monotonicity, a useful index is Kendall's coefficient of concordance, W, computed separately for the row rankings (Wr,) and the column rankings (Wc.) (Wallsten, 1976). The value of W may be roughly interpreted as the mean rank-order correlation between all possible pairs of row (column) ranks. In a perfectly additive matrix, Wr = Wc = 1. The greater the number of violations of monotonicity, the closer these coefficients will be to 0.
The second ordinal property helpful in diagnosing departures from additivity is the double cancellation condition. Double cancellation holds whenever the following relation exists:
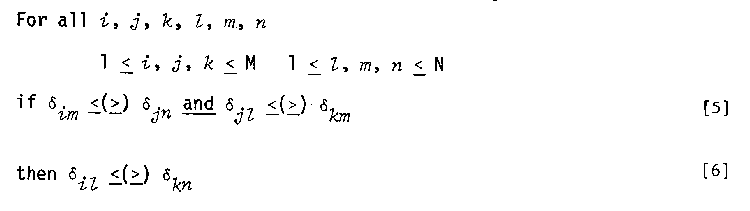
The double cancellation condition is satisfied whenever the two antecedent inequalities in Equation S are followed by the inequality in Equation 6. Double cancellation is illustrated in Figure 1.
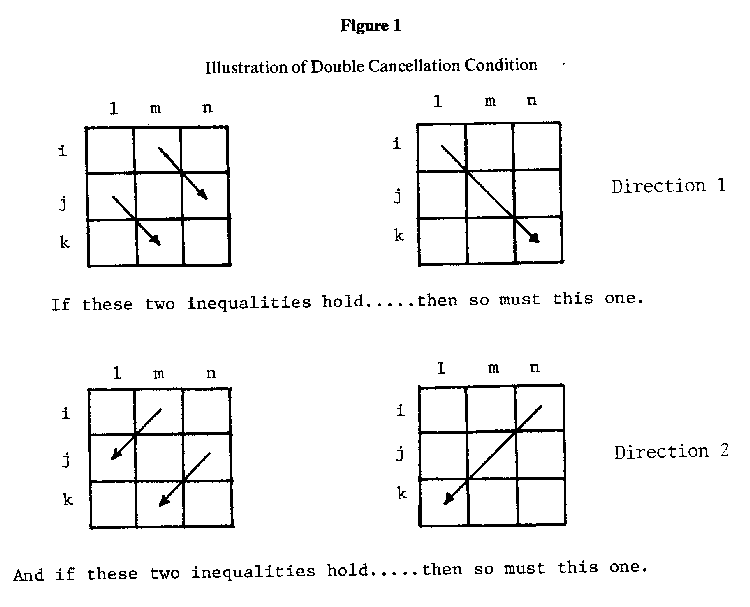
Double cancellation can be tested by examining all 3x3 submatrices generated from the intersection of any 3 rows and any 3 columns of the MxN data matrix. There are (M,3) . (N,3) 3x3 submatrices to examine. Each of these can be classified into one of three categories:
1. Double cancellation satisfied: The two antecedent inequalities of Equation 5 hold and the inequality of Equation 6 holds.
2. Double cancellation violated: The two antecedent inequalities of Equation 5 hold but not the inequality of Equation 6.
3. Not testable: The antecedent inequalities of Equation 5 do not hold, i.e., either dim < djn and djl > dkm or else dim > djn and djl < dkm.
The ratio of the number of submatrices with cancellation violations to the total number of testable submatrices gives another diagnostic index of how much the data matrix departs from perfect additivity. In the perfect case, this ratio will be 0.
Note that if monotonicity holds and the data matrix is arranged so that its elements increase from left to right and from top to bottom, then double cancellation in Direction 1 (Figure 1), but not Direction 2, follows as a consequence. Thus, in this situation double cancellation in Direction 2 is more difficult to achieve and, hence, the sharper test of additivity. However; both monotonicity and double cancellation are only necessary, not sufficient, conditions for additivity. There is no guarantee that the matrix is additive even if Wr = Wc = 1 and there are no violations of double cancellation in either direction. (For an example of a matrix which satisfies monotonicity and double cancellation but which is not additive, see Blair. O'Connor, and Pollatsek (1970, p. 19).) Necessary and sufficient conditions for additivity are given by Scott (1964) and Tversky (1967).
Analysis of the Parole Data
The first set of data is an experience table currently used by the United States Board of Parole for parole decisions. As an aid to parole prognosis, Hoffman and Beck (1974) cross-tabulated 66 variables with parole outcome for a sample of approximately 2500 released convicts. The 9 variables found to relate most to outcome and judged to pose no ethical problems in their use by the Board were combined into a "Salient Factor" instrument. For the present analysis all 9 variables (items) have been scored dichotomously. These items and the rules for scoring them are given in Table 1.
| Table 1 Description of Items Used and Scoring Rules for Parole Data | ||
|---|---|---|
| Item Score | Score | |
| 1. | Grade Claimed Has completed 12th grade or received GED Otherwise | 1 0 |
| 2. | Auto Theft Commitment offense did not involve auto theft Otherwise | 1 0 |
| 3. | Age at First Commitment 18 years or older Otherwise | 1 0 |
| 4. | Prior Incarcerations Two or less prior convictions Three or more prior convictions | 1 0 |
| 5. | Drug History No history of opiate or barbiturate usage Otherwise | 1 0 |
| 6. | Planned Living Arrangement Release plan to live with spouse and/or children Otherwise | 1 0 |
| 7. | Employment Verified employment (or full-time school attendance) for a total of at least 6 months during last 2 years in the community. Otherwise | 1 0 |
| 8. | Prior Convictions Two or less prior convictions Otherwise | 1 0 |
| 9. | Parole Revoked Never had parole revoked Otherwise | 1 0 |
Table 2 gives the proportions, Pij, of individuals with raw score i who passed item j, based on a sample of 490 subjects. The items have been arranged in increasing order of easiness from left to right. The data matrix in Table 2 was used as input to Kruskal's MONANOVA program, with Row 9 eliminated. This row represents the 8 individuals who received the maximum score, 9; since Rasch scaling does not estimate person parameters for perfect or 0 scores, they were excluded from the analysis.
| Table 2 Proportion of Correct Answers for Each Item in Groups by Raw Score for Parole Data | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Raw Score | Item | Number of persons with each raw score | ||||||||
| 6 | 1 | 8 | 7 | 4 | 9 | 2 | 3 | 5 | ||
| 1 | .00 | .00 | .00 | .00 | .00 | .00 | .27 | .00 | .73 | 15 |
| 2 | .06 | .04 | .04 | .19 | .06 | .23 | .51 | .21 | .64 | 47 |
| 3 | .07 | .15 | .08 | .39 | .18 | .33 | .61 | .52 | .67 | 61 |
| 4 | .18 | .24 | .12 | .40 | .52 | .51 | .64 | .68 | .70 | 84 |
| 5 | .13 | .33 | .30 | .51 | .73 | .68 | .68 | .84 | .78 | 82 |
| 6 | .13 | .28 | .64 | .58 | .95 | .91 | .77 | .97 | .78 | 86 |
| 7 | .17 | .47 | .85 | .82 | 1.00 | .93 | .90 | .97 | .90 | 60 |
| 8 | .17 | .85 | 1.00 | .98 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 47 |
| 9 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 8 |
| 490 | ||||||||||
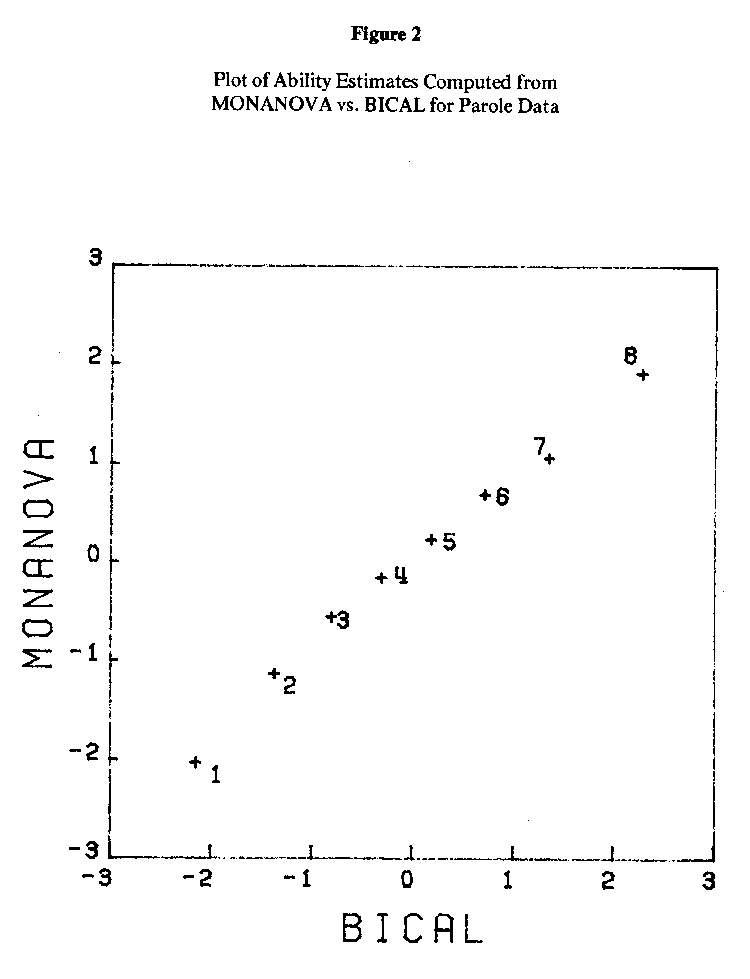
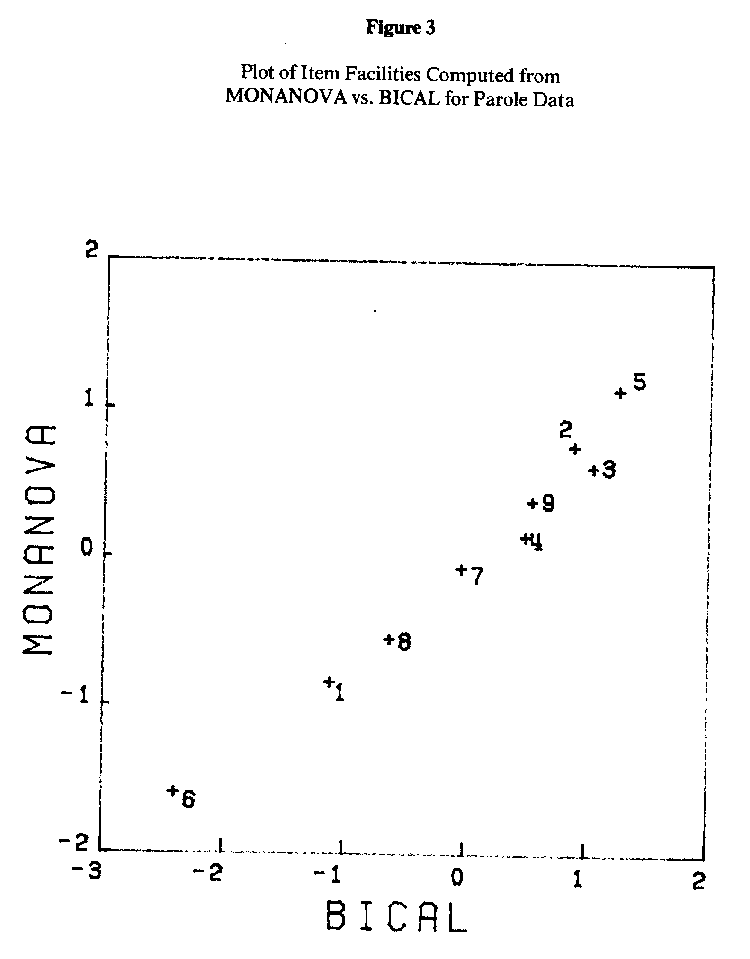
MONANOVA finds the best (minimum stress) ascending monotone function M for producing an additive representation of the matrix of proportions. Row and column effects are computed using ANOVA on the transformed values M(Pij). The row effects are the person parameters or "abilities." (In the present context, these ability estimates attempt to measure a latent trait which might be labeled "the ability to successfully complete parole without any violations.") The column effects are the item parameters (facilities). Estimates of the person and item parameters were also obtained using the program BICAL (Wright & Mead, 1977), which does Rasch scaling by the method of unconditional maximum likelihood. The MONANOVA and BICAL ability estimates have been plotted against each other in Figure 2; Figure 3 is a plot of the two sets of item facilities (BICAL actually computes item difficulties, which are the negative of the item facilities shown here).
Figure 2 shows that the two sets of ability estimates calculated from MONANOVA and BICAL had an almost perfect linear relationship: Their correlation is .997. Figure 3 shows the same for the two sets of item facilities. Their correlation is .985.
Tests of Fit for the Parole Data
The tests of fit lead to some interesting questions. The fit analysis for the Rasch model estimates can be organized into three components: (1) an overall analysis of total test fit; (2) a partition of this analysis into the fit of each item; and (3) a specific test of the invariance of the item estimates over score (ability) groups (Wright & Mead, 1977).
The Overall Fit Mean Square is the average over all persons and items of the squared standardized residual. The squared standardized residual for person i on item j is given by:

Summing over N persons and L items and dividing by the degrees of freedom (N-1)(L-1) gives the Overall Fit Mean Square:

which is distributed approximately as a mean square statistic with expected value of 1 and a standard error equal to sqrt(2/(N-1)(L-1)). For the parole data, v. = .91 (S.E. = .02), indicating a fit which is really too good.
This mean square can be partitioned to focus on the items individually. The Fit Mean Square for item j, vj, is

which is distributed approximately as a mean square with expected value of 1 and a standard error equal to sqrt(2L/(N-1)(L-1)). The item Fit Mean Squares for the 9 parole items are shown in Table 3.
| Table 3 Fit Mean Squares for the Nine "Salient Factor" Items in the Parole Sample | |
|---|---|
| Item | Fit Mean Square |
| 1 | .96 |
| 2 | 1.00 |
| 3 | .66 |
| 4 | .60 |
| 5 | 1.13 |
| 6 | 1.52 |
| 7 | .94 |
| g | .67 |
| 9 | 74 |
Items with Fit Mean Square less than 1 + 2 (standard error) behaved pretty much as the model predicted. By this criterion, only Item 6 (vb = 1.52, S.E. = .07) fit poorly. But Items 3, 4, 8, and 9 fit too well.
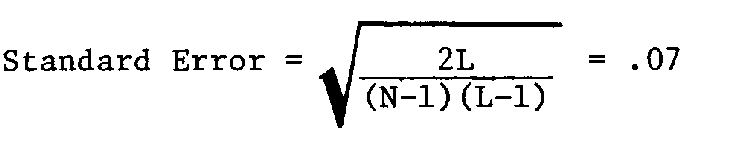
When the model holds, estimates of item parameters should be independent of the distribution of person ability. By dividing the sample into groups based on score levels and checking for group differences in the residuals, the stability of item parameters over ability levels can be tested. BICAL does this by computing ANOVAs for the residuals inflated to have individual degrees of freedom of one for each of the items. The ratio of the between-groups to within-groups mean squares of these residuals is distributed approximately as an F statistic with k and N-k degrees of freedom, where k is the specified number of score groups used in the analysis and N is the sample size. A significant F for an item indicates that its facility parameter is not stable over ability levels.
The parole sample was analyzed using the six scoring groups: 1-2, 3, 4, 5, 6, 7-8. The hypothesis of stability over ability levels could be rejected (p < .01) for 6 of the 9 items (3, 4, 5, 6, 8, 9). This qualifies the two previous tests of fit and implies that the data did not conform fully to the model's predictions.
In summary, the parole data appeared to fit overall, and all but Item 6 appeared to fit among the items. However, when the specific test for item stability over score groups was performed, then it can be seen that there were serious signs of item instability. In practice, as can be seen here, the use of statistical tests of goodness-of-fit are not so clear-cut as might be inferred from the earlier remarks contrasting the statistical Rasch model with the deterministic additive conjoint measurement model.
The various tests of additivity which were used were in agreement that the conjoint measurement model did not hold up too well. The stress value computed for MONANOVA was 27.1%. In another context Kruskal (1964) has proposed that stress as large as 20% indicates a poor fit. Stress corresponds to the Overall Fit Mean Square, v., discussed above. It would be possible to compute components of stress (or more conveniently, stress squared) due to separate items or score groups. Resolving stress in components by item or score group would be helpful in identifying bad-fitting items and score groups. It would also be informative to see the extent to which the item fit statistics agree with the item stress components in indicating the good- and bad-fitting items. In the present example, the favorable value of v. did not agree with the high stress value.
This guideline for interpreting stress values has been given in reference to the closely allied field of nonmetric multidimensional scaling. Although there are monte carlo studies which help to explicate the interpretation of stress values in multidimensional scaling models, none has been reported for conjoint measurement.
The tests for monotonicity were consistent with the high stress value: Wr = .895 and Wc = .695. Apparently, the columns of the data matrix in Table 1 departed appreciably from perfect monotonicity, although the meaning of these magnitudes will be more understandable when they are considered in comparison to the values computed in the second data set below.
Similarly, the cancellation tests gave poor results. The data matrix consists of (;) (;) = 4704 3x3 submatrices which were examined for violation of cancellation. Each submatrix was examined in both directions (see Figure 1). The results of the cancellation tests are given in Table 4.
| Table 4 Results of Cancellation Tests for Data Matrix of Table 1 | |||
|---|---|---|---|
| Number of Matrices | Direction | Total | |
| 1 | 2 | ||
| Not testable | 146 | 1788 | 1934 |
| Satisfying cancellation | 4555 | 2226 | 6781 |
| Violating cancellation | 3 | 690 | 693 |
| 4704 | 4704 | 9408 | |
| Violations/Testable | .0007 | .2366 | . 0927 |
However, it is probably more informative to consider just the cancellation tests in Direction 2. Cancellation tests in Direction 1 are considerably constrained to be favorable as long as monotonicity is "reasonably" well satisfied, and although it has been seen that Wc was not too close to 1, it was certainly very far from 0. Using Direction 2 only, then, gives a ratio of total violations to total testable submatrices of 690/2916 = .24. No statistical significance can be assigned to this value. However, as a baseline for comparison, Levelt, Riemersma, and Bunt (1972) analyzed some empirical data in the same way and found ratios in the range of .002 to .026. Using this baseline, the parole data fall well short of a good fit.
Summarizing all the results, both the statistical tests of fit and the tests of additivity imply that the data were not too well described by an additive representation. On the other hand, the very high agreement between the MONANOVA and BICAL parameter estimates suggested that despite the poor fit of the data, the Rasch model performed close to optimally (i.e., the minimum stress monotonic function which best produces additivity in these data was extremely close to a linear transformation of the logistic function).
Reanalysis of an Example from Rasch
To provide a contrast with the parole data, some data given by Rasch (1960, p. 71) were reanalyzed. This example was selected because Rasch (1960, p. 91) asserts that "on the whole the model gives a satisfactory description of the data."
The data used were from the testing of 1094 Danish military recruits administered one subtest of a group intelligence test. Rasch did not state so explicitly, but this test apparently consisted of free-response items (Rasch, 1960, p. 62). When this is not the case, that is, when multiple-choice questions are used, the model's assumptions are violated. This occurs because the probability of correctly responding to an item should approach 0 for low ability levels; for multiple-choice items, this probability usually approaches a constant-one over the number of alternatives-due to random guessing among alternatives. (Clearly, this was not a problem to consider for the demographic items used in the first analysis.) This point will not be pursued further, but the model can often be usefully applied even where its assumptions are not met exactly.
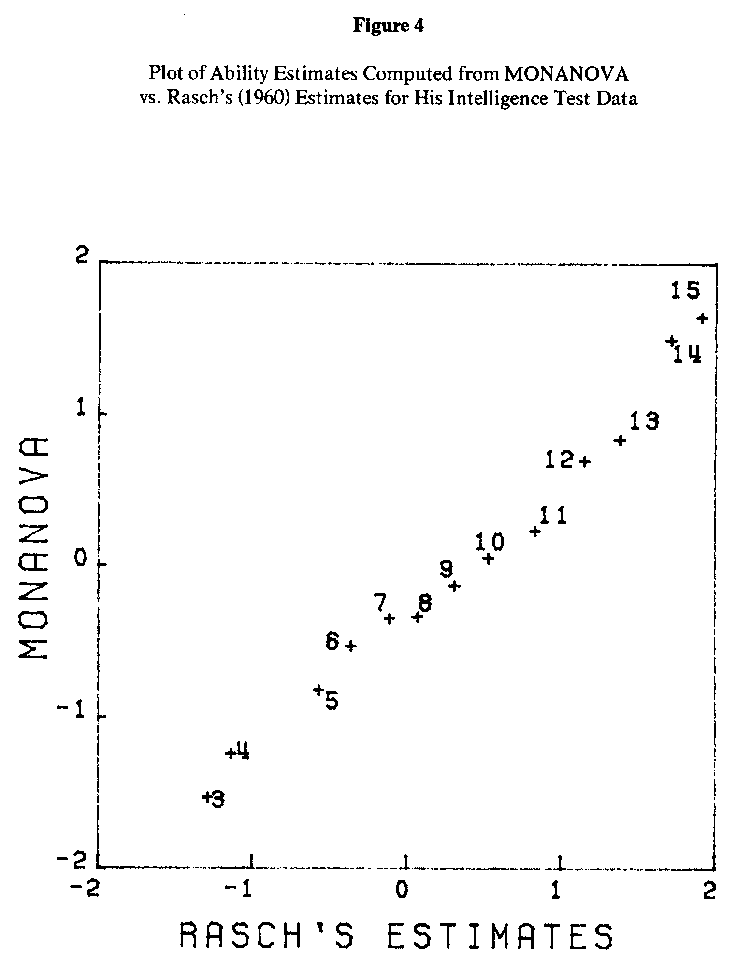
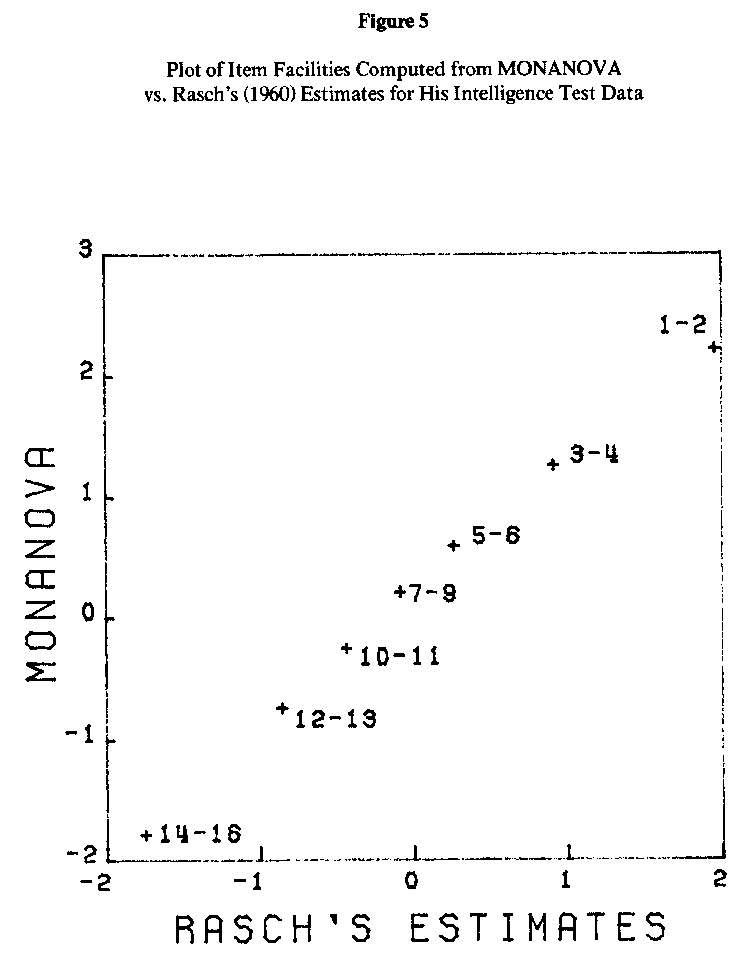
Rasch smoothed the data by pooling items together from the 16-item test. His data are presented in Table 5. This data matrix was also analyzed using MONANOVA. The person abilities and item facilities computed from MONANOVA have been plotted against the estimates given by Rasch (1960, p. 106), and appear in Figures 4 and 5. The estimation methods Rasch used in his analysis were, by his own admission, "primitive"; in part, they were obtained by fitting graphical data by sight. However, he remarked that they matched very closely with estimates obtained more rigorously, and they are sufficiently accurate for our purposes here.
| Table 5 Average Proportion Correct for Item Groups and Raw Score for Data Adapted from Rasch (1960) | ||||||||
|---|---|---|---|---|---|---|---|---|
| Raw Score | Item | Number of persons with each raw score | ||||||
| 14-16 | 12-13 | 10-11 | 7-9 | 5-6 | 3-4 | 1-2 | ||
| 3 | .00 | .01 | .00 | .01 | .06 | .48 | .92 | 49 |
| 4 | .00 | .00 | .02 | .04 | .11 | .84 | .98 | 112 |
| 5 | .00 | .04 | .07 | .12 | .40 | .84 | .98 | 32 |
| 6 | .00 | .05 | .07 | .21 | .70 | .86 | .99 | 76 |
| 7 | .02 | .09 | .24 | .42 | .70 | .86 | .98 | 82 |
| 8 | .01 | .09 | .28 | .62 | .79 | .90 | .99 | 102 |
| 9 | .02 | .16 | .45 | .73 | .84 | .95 | .99 | 119 |
| 10 | .03 | .28 | .59 | .83 | .88 | .96 | 1.00 | 133 |
| 11 | .06 | .39 | .76 | .90 | .94 | .98 | 1.00 | 123 |
| 12 | .09 | .66 | .87 | .93 | .95 | .99 | 1.00 | 94 |
| 13 | .23 | .80 | .90 | .98 | .98 | .99 | 1.00 | 61 |
| 14 | .35 | .91 | 1.00 | 1.00 | 1.00 | 1.00 | 1.00 | 17 |
| 15 | .70 | .85 | .95 | 1.00 | 1.00 | 1.00 | 1.00 | 10 |
| 1060 | ||||||||
Once again, the plots in Figures 4 and 5 reveal an almost perfect linear correspondence between the different methods. The correlation between the two sets of ability estimates was .990; the item facilities correlated .997.
Goodness-of-fit for Rasch's Example
Rasch's graphical tests of fit for these data are rather crude, but sufficient to demonstrate that the model holds up well. Consequently, it should follow that tests for additivity are favorable, too.
The analysis here confirms Rasch's conclusions. The stress value computed by MONANOVA was 9.5%, considerably better than the 27.1% for the parole data. The tests for cancellation are given in Table 6 and also reflect considerable improvement in additivity compared to the previous example.
| Table 6 Results of Cancellation Tests for Rasch's Data | |||
|---|---|---|---|
| Number of Matrices | Direction | Total | |
| 1 | 2 | ||
| Plot testable | 0 | 4424 | 4424 |
| Satisfying cancellation | 10010 | 4961 | 14971 |
| Violating cancellation | 0 | 625 | 625 |
| 10010 | 10010 | 20020 | |
| Violations/Testable | .0000 | .1119 | . 0401 |
The ratio of total violations to total testable submatrices in Direction 2 was 625/5586 = .11, less than half the value (.24) for the parole data.
The tests for monotonicity parallel these results: Wr= .921 and Wc = .967. The marked increase in monotonicity over the first example provides still further evidence that the Rasch data were more consistent with an additive model.
Measurement on an Interval Scale with Common Unit
The Rasch model, when it holds, yields measures of person abilities and item facilities on an interval scale with a common unit. There is an equivalent result from the theory of conjoint measurement (Coombs, Dawes, & Tversky, 1970) which states that when additivity exists, then all independent variables are measured on an interval scale with a common unit.
This could be empirically tested with the two data sets analyzed here. Assuming the data conform to the Rasch model, the ability estimates {ai} obtained from MONANOVA should be a positive linear transformation of the estimates {ai} obtained by Rasch scaling: a = ka' + l where k > 0. Similarly, the MONANOVA item facilities {bj} should be related to the Rasch scaled item facilities {b'j} by b = mb' + n where m > 0. It has been seen that in both examples these linear relations held up remarkably well. However, by the common unit hypothesis, k should equal m. Empirically, this means that the regression slope of a on a' should be approximately equal to the regression slope of b on b'.
These regression slopes are listed in Table 7.
| Table 7 Regression Slopes of MONANOVA Estimates on Corresponding Rasch Scaled Estimates | ||
|---|---|---|
| Data | Subject Abilities | Item Facilities |
| Parole Data | .86 | .72 |
| Rasch Data | .93 | .92 |
The discrepancy between .86 and .72 for the parole data can be attributed to the poor fit of the model. In contrast, for Rasch's example, where the model fits well, the two slopes were almost identical (.93 and .92).
Conclusion
The primary intention of this paper has been to make better known the occasionally noted, but not widely appreciated, connection between Rasch's psychometric model and additive conjoint measurement. The proven usefulness of the Rasch model in a variety of areas demonstrates that conjoint measurement is of more than theoretical interest. Many situations where subjects respond to stimuli could potentially fit the paradigm, and there are no doubt possible applications of value to psychologists with rather different substantive concerns (Rasch, 1966).
References
Andersen, E. B. Conditional inference and models for measuring. Copenhagen, Denmark: Mentalhygiejnisk Forlag, 1973.
Andersen, F. B. Sufficient statistics and latent trait models. Psychometrika, 1977, 42, 69-82.
Blair, W. C., Jr., O'Connor, M. F., & Pollatsek, A. W. A workbook for mathematical psychology: An elementary introduction. Englewood Cliffs, NJ: Prentice-Hall, 1970.
Brogden H. E. The Rasch model, the law of comparative judgment, and additive conjoint measurement. Psychometrika. 1977, 42, 63135.
Cliff, N. M. Scaling. Annual Review of Psychology. 1973, 24. 473-505.
Coombs, C. H., Dawes, R. M., & Tversky, A. Mathematical psychology: An elementary introduction. Englewood Cliffs, NJ: Prentice-Hall, 1970.
Falmagne, J. Random conjoint measurement and loudness summation. Psychological Review, 1976, 83. 65-84.
Fischer, G. Psychologische testtheorie. Bern: Huber, 1968.
Haberman, S. Maximum likelihood estimates in exponential response models. Annals of Statistics, 1977, 5, 815-841.
Hoffman, P. B., & Beck, J. L. Parole decision making: A salient factor score. Journal of Criminal Justice. 1974, 2. 195-206.
Keats, J. A. Test theory. Annual Review of Psychology, 1967,18. 217-238.
Keats, J. A. An introduction to quantitative psychology. Sydney, Australia: John Wiley & Sons Australasia Pty. Ltd., 1971.
Krantz, D. H., Luce, R. D., Suppes, P., & Tversky, A. Foundations of measurement. Vol. I: Additive and polynomial representations. New York: Academic Press, 1971.
Kruskal, J. B. Multidimensional scaling by optimizing goodness-of-fit to a nonmetric hypothesis. Psychometrika, 1964, 29. 1-27.
Kruskal, J. B. Analysis of factorial experiments by estimating monotone transformations of the data. Journal of the Royal Statistical Society (Series B), 1965, 27. 251-263.
Kruskal, J. B., & Carmone, F., Jr. MONANOVA: A FORTRAN-IV program for monotone analysis of variance. Behavioral Science. 1969, 14. 165-166.
Levelt, W. J. M., Riemersma, J. B., & Bunt, A. A. Binaural additivity of loudness. British Journal of Mathematical and Statistical Psychology, 1972, 25, 518.
Lord, F. M., & Novick, M. R. Statistical theories of mental test scores. Reading, MA: Addison-Wesley, 1968.
Luce, R. D., & Tukey, J. W. Simultaneous conjoint measurement: A new type of fundamental measurement. Journal of Mathematical Psychology, 1964, 1, 1-27.
McClelland, G. H., & Coombs, C. H. ORDMENT: A general algorithm for constructing all numerical solutions to ordered metric structures. Psychometrika, 1975, 40, 269-290.
Rasch, G. Probabilistic models for some intelligence and attainment tests. Copenhagen, Denmark: Danmarks Paedogogische Institut, 1960.
Rasch, G. An item analysis which takes individual differences into account. British Journal of Mathematical and Statistical Psychology. 1966, 19, 49-57.
Scott, D. Measurement models and linear inequalities. Journal of Mathematical Psychology, 1964, 1, 233-247.
Tversky, A. A general theory of polynomial conjoint measurement. Journal of Mathematical Psychology, 1967, 14. 144-185.
Wallsten, T. Using conjoint-measurement models to investigate a theory about probabilistic information processing. Journal of Mathematical Psychology-1967,14,144-185.
Wright, B., & Douglas, G. A. Best procedures for sample-free item analysis. Applied Psychological Measurement, 1977, 1, 281-295.
Wright, B., & Mead, R. J. BICAL: Calibrating items and scales with the Rasch model (Research Memorandum No. 23). University of Chicago, Department of Education, Statistical Laboratory, 1977.
Wright, B., & Panchapakesan, N. A procedure for sample-free item analysis. Educational and Psychological Measurement, 1969, 29, 23-48.
Young, F. W. A model for polynomial conjoint analysis algorithms. In R. B. Shepard, A. K. Romney, & S. B. Nerlove (Eds.), Multidimensional scaling. Theory and applications in the behavioral sciences. New York: Seminar Press, 1972.
Acknowledgments
We want to thank Dr. R. D. Bock, University of Chicago; Dr. Clyde Coombs, University of Michigan; Dr. Donald Fiske. University of Chicago; and Dr. Thomas Wallsten. University of North Carolina, for reading and commenting upon an earlier version of this paper. Part of the research,for our analyses was supported by Grant No. 78-NI-AX-0047 from the Law Enforcement Assistance Administration to Howard Wainer.
This paper was published in Applied Psychological Measurement, 1979, 3:2, 237-255
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo24.htm