Science conquers experience by finding the most succinct explanations to which experience can be forced to yield. Progress marches on the invention of simple ways to handle complicated situations. When a person tries to answer a test item the situation is potentially complicated. Many forces might influence the outcome - too many to be named in a workable theory of the person's response. To arrive at a workable position, we must invent a simple conception of what we are willing to suppose happens, do our best to write items and test persons so that their interaction is governed by this conception and then impose its statistical consequences upon the data to see if the invention can be made useful.
Latent trait models for person measurement are inventions that claim to specify what happens when a person tries an item. Each model has its own particular ingredients and so asserts that other possibilities can be overlooked or controlled. But which ingredients are essential? Where should adding more ingredients stop? Should there be as many person parameters as item parameters? If item "discrimination" is needed, then why not person "sensitivity"? Is "guessing" provoked by items or imposed by persons?
UNDERSTANDING THE RASCH MODEL
Of all latent trait models proposed for person measurement, the Rasch model has the fewest ingredients, just one ability parameter Bn for each person n and one difficulty parameter Di for each item i. These parameters represent the positions of persons and items on the latent variable they share. They are used in the model to determine the probability of person n succeeding on item i (Rasch 1960, pp. 62-125; 1966a; 1966b; Wright, 1968).
If the variable were length, Bn could represent the height of person n, Di could represent the length of measuring stick i, and measurement could consist of holding sticks of various lengths against the persons to be measured to see which ones they surpass and which ones they fail to surpass. We would measure them by finding the pair of sticks which seem to bracket the tops of their heads most closely and interpolating between them or by letting the length of the sticks that seem nearest to the tops of their heads become their "heights."
Putting the Model Together
The way Bn and Di are combined is by forming their difference (Bn-Di). This difference governs the probability of what is supposed to happen when person n pits his ability against the difficulty of item i. Since either parameter can vary from minus infinity to plus infinity, so can their difference. But probability must stay between zero and one. To deal with this, the difference (Bn-Di) is applied as the exponent of a base, e(Bn-Di), and this term is used in the ratio e(Bn-Di)/[1+e(Bn -Di)] which is the Rasch probability for a right answer.

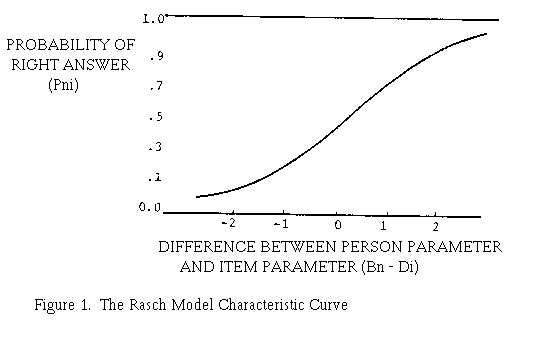
Figure 1 is a picture of the way this probability Pni depends on the difference between person ability Bn and item difficulty Di. Table 1 gives numerical examples of this relationship.
When person n has more of the latent ability than item i requires, then Bn is more than Di, their difference is positive and person n's probability of success on the item is greater than 0.5. The more person n's ability surpasses the item's ability requirement, i.e. its difficulty, the greater this positive difference and the higher is person n's probability of success. But when the item is too difficult for person n, then Bn is less than Di, their difference is negative and person n's probability of success is less than 0.5. The more difficult item i is for person n, the greater this negative difference becomes and the lower is person n's probability of success. (In future references, we shall drop the subscript n on Bn and the subscript on Di: application to persons and items, respectively, will be understood.)
| Table 1 | |||||
|---|---|---|---|---|---|
| The Rasch Probability of a right answer as a Function of Person Ability and Item Difficulty and the Information in a Response | |||||
| Person Ability B | Item Difficulty D | Different B-D | Odds e(B-D) | Right Answer Probability P | Information in a Response |
| 5 4 3 2 1 0 0 0 0 0 0 |
0 0 0 0 0 0 1 2 3 4 5 |
5 4 3 2 1 0 -1 -2 -3 -4 -5 |
148. 54.6 23.1 7.39 2.72 1.00 .368 .135 .050 .018 .007 |
.99 .98 .95 .88 .73 .50 .27 .12 .05 .02 .01 |
.01 .02 .05 .11 .20 .25 .20 .11 .05 .02 .01 |
If item difficulty is held constant and person ability is varied, Figure 1 provides a picture of the way the probability of success on that item changes as a function of person ability. This is an item characteristic curve in its simplest form. If person ability is held constant and item difficulty is varied, then Figure 1 provides a picture of the way a particular person is expected to perform on items of various difficulties. This is a person characteristic curve.
If the answer person n gives to item i is expressed as Xni=1, for "right," and Xni=0, for "wrong," then the Rasch model for measuring persons and calibrating items becomes:
Pr {Xni | Bn, Di} = eXni(Bn-Di)/[1 + e(Bn-Di)] (1)
Ultimately, the particular units applied to measuring persons (and calibrating items) come from how the variable is defined by the particular items selected to operationalize it. Were length the variable, then person height Bn and measuring stick length Di might be in inches or centimeters or any other unit of length which had been agreed upon and specified by "standard" sticks. The model itself, however, through its mathematical form, defines a general unit which is quite convenient to work with and is easily transformed into whatever applied units are subsequently defined. This general mathematical unit is called a "logit". A person's ability in logits is their natural loge odds for succeeding on items of the kind chosen to define the scale origin or "zero." Thus the person's probability P for succeeding on an item with difficulty Di=0 is eB/(1 + eB) from which their success odds are P/(1-P) = eB, the natural loge of which is B.
Similarly, an item's difficulty in logits is the natural log odds for failure on that item by persons with abilities at the scale origin. The probability P of these persons with abilities at B=0 of succeeding on an item with difficulty D is e-D/(1 + e-D) from which their odds for failure are (1-P)/P = eD, the natural loge of which is D.
The first six rows of Table 1 give examples of abilities in logits and their associated odds and probabilities of success when persons of these abilities encounter items that have a difficulty at "zero". Similarly, the last six rows of Table 1 give examples of difficulties in logits and their associated odds and probabilities of success when attempted by persons at ability "zero".
Since it is the difference (B-D) which governs the probability of a right answer, we can add or subtract any constant we wish to all abilities and difficulties without changing the bearing of their difference on the probability of success. Thus the location of "zero" on the scale of the latent variable is up to us. We can place "zero" so that negative difficulties and abilities do not occur, or at the easiest item or least able person, or at the mean difficulty of all calibrated items or all measured persons. We can also introduce any scaling factor we find convenient, including one which avoids decimal fractions.
A handy translation and scaling to new units, called "WITs", provides units which can be satisfactorily expressed in terms of positive integers. The transformation is DW = (100 + 9.1D) and BW = (100 + 9.1B). WITs have the appealing feature that differences between ability and difficulty in tens relate to right answer probabilities in the easy to remember steps of P = .10 for (B - D) = -20, .25 for - 10, .50 for 0, .75 for +10 and .90 for +20. (For more on units see Woodcock, 1973, 51-56; Wilmott and Fowles, 1974, 51-53; Wright and Douglas, 1975a, 47-54.)
The last column of Table 1 gives the relative "information" I = P(1-P) available in a response observed at particular (B-D) values. When item difficulty D is within a logit of person ability B, so that |B-D|<1, the information about either D or B is greater than .20. But when item difficulty is more than two logits away from B; i.e. "off-target," so that |B-D|>2, the information is less than .11 and for |B-D|>3 I is less than .05. The implications for efficient calibration sample design and best test design are that responses in the |B-D|<1 region are worth twice as much for calibrating items or measuring persons as those for which |B-D|>2 and four times as much as those for which |B-D|>3.
Estimating item Difficulty and Person Ability
Mathematical analysis shows the Rasch model to be statistically strong. It has estimators for its parameters, Bn and Di, that are sufficient, consistent, efficient and unbiased (Rasch, 1968; Andersen, 1970, 1972, 1973). Numerical analysis supports simple approximations for estimating these parameters which are accurate enough for all practical purposes (Wright and Douglas, 1975b, 1977a, 1977b). Experience has shown the model to be easy to apply in a wide variety of situations (Connolly, Nachtman, and Pritchett, 1971; Woodcock, 1974; Wilmott and Fowles, 1974; Rentz and Bashaw, 1975; Andrich, 1975; Mead, 1976). Technical details are described in Wright and Panchapakesan (1969), Wright and Mead (1975, 1977), and Wright and Douglas (1975a, 1975b, 1976, 1977b).
An efficient method for approximating parameter estimates (Cohen, 1976) that can easily be completed by hand is as follows:
1. For a test of L' items given to a sample of N' persons: delete all items that no one gets right or no one gets wrong and all persons with no items right or no items wrong and continue deleting until no such items or persons remain. For the L items and N persons remaining:
2. Observe si the number of persons who got item i right, for i = 1 through L and nr the number of persons who got r items right, for r = 1 through L-1.
3. Calculate xi = ln[(N-si)/si] the loge ratio of wrong to right answers to item i by N persons, (2)
x = sum(xi/L) i=1,L, the mean of xi over L items, (3)
U = sum(xi - x.)²/(L-1) i=1,L, the variance of xi over L (4)
yr = ln[r/(L-r)] the loge ratio of right to wrong answers on L items, (5)
y. = sum(nryr/N) r=1,L-1, the mean of yr over N persons, (6)
V = sum(nr(yr-y.)²/(N-1) r=1,L-1, the variance of yr over N persons, (7)
4. Let X² = (1+U/2.89)/(1-UV/8.35) an expansion factor due to variation in item difficulty, (8)
Y² = (1+V/2.89)/(1-UV/8.35) an expansion factor due to variation in person ability, (9)
5. Then di = Y(xi-x.) the difficulty estimate of item i, (10)
SE(di)² = Y²[N/si(N-si)] the standard error of difficulty calibration, (11)
br = Xyr the ability estimate implied by score r, (12)
SE(br)² = X²[L/r(L-r)] the standard error of ability measurement (13)
As an example of this procedure, suppose 448 persons took a five item test with responses as shown under si and nr in Table 2. Calculation of U, V, X and Y produce the di and br values listed. Since the data were generated by simulating the exposure of randomly selected persons with mean ability zero and standard deviation 0.5 to five items with the difficulties shown under Di, the success of the calibration can be judged by comparing the estimated di with corresponding "generating" Di.
| Table 2 | |||||
|---|---|---|---|---|---|
| An Example of Rasch Model Calibration | |||||
| Item | si | xi | di=Y(xi-x.) | SE(di) | Di |
| 1 2 3 4 5 |
321 296 233 168 138 |
-0.93 -0.67 -0.08 0.51 0.81 |
-0.99 -0.69 -0.01 0.67 1.01 |
0.12 0.11 0.11 0.11 0.12 |
-1.00 -0.50 -0.00 0.50 1.00 |
| N=448 x.=-0.07 U=0.55 X=1.12 | |||||
| Score | nr | yr | br=Xyr | SE(br) | |
| 1 2 3 4 |
63 146 155 84 |
-1.39 -0.41 0.41 1.39 |
-1.56 -0.46 0.46 1.56 |
1.25 1.02 1.02 1.25 |
|
Analyzing item and Person Fit
The fit of data to the Rasch model can be evaluated by calculating how much is "left over" after the data have been used to estimate item difficulties di and person abilities bn = br, where r is the test score of person n. The standardized square of this residual after fitting the model is e(bn-di), for a wrong answer and e(di-bn), for a right one. The average degrees of freedom of each residual are (L-1)(N - 1)/LN. These squared residuals can be summed over persons or items to form approximate chi-square distributed variables for testing the fit of any particular item to any group of persons, or of any individual person to any set of items.
Even the residual for a single person-item encounter can suggest that the encounter may have departed from expectation to an extent worth noting and, perhaps, correcting for. When persons for whom (bn-di) is greater than three nevertheless fail, the probability of their wrong answers is 1/(1+e3) = 1/21. We may wonder how those persons could have missed an item that was so easy for them and investigate to see whether some unplanned influence interfered with the application of their ability to that item. Were those persons distracted, out of practice, rushed, bored? Or was the item biased against them?
Similarly when persons for whom (di-bn) is greater than three nevertheless succeed, the probability of this event is also only 1/21 and we may wonder how those persons accomplished such an unlikely success. Were they specially prepared for this item? Were they guessing or cheating? Or was the item biased in their favor?
A more extensive analysis of the response pattern of each person can be implemented by evaluating the way in which their residuals correlate with item difficulty, position and type. For this we can use standardized residuals in their unsquared form: -e+(bn-di)/2 for a wrong answer and +e+(bn-di)/2, for a right one. Since these residuals are standardized, that is centered at their expected mean and scaled by their expected standard deviation, their expected distribution can be modeled as approximately normal and their expected error variance as one.
WHY THE RASCH MODEL IS DIFFERENT FROM OTHER LATENT TRAIT MODELS
The Rasch model follows from the assumption [Wright now prefers "specification"] that the unweighted sum of right answers given by a person will contain all of the information needed to measure that person and that the unweighted sum of right answers given to an item will contain all of the information needed to calibrate that item. The Rasch model is the only latent trait model for a dichotomous response that is consistent with "number right" scoring. Mathematical proofs of this uniqueness are given by Rasch (1968) and Andersen (1973). All of the other latent trait models lead to more complex scoring rules that involve unknown parameters for which satisfactory estimators do not exist.
Like Rasch, the other models specify just one person parameter and use an exponential function of person and item parameters to define the probability of a successful response. However the other models introduce additional item parameters. A parameter for variation in the slope of the item characteristic curve is introduced to allow items to differ in their power to discriminate among persons. Another parameter for variation in the lower asymptote of the item characteristic curve is introduced to allow items to differ in how much guessing they provoke. Comparable person parameters could equally well be introduced; i.e., a slope parameter for the person characteristic curve to represent "person sensitivity" to item difficulty and another asymptote parameter representing a person's inclination to guess. Unfortunately, additional parameters like these, whether for items or persons, wreak havoc with the logic and practice of measurement.
A useful way to understand the measurement logic defended by the Rasch model is to ask how we want to think about the relative performance of two persons. Do we want to think that the more able one has a better chance for success no matter what the difficulty of the attempted item? Is that what we intend "more able" to mean? If so, we must see to it that variation in person sensitivity does not express itself in the measuring situation, for we do not want person characteristic curves that cross one another. Variation in person sensitivity will produce variation in slope which will produce crossed curves. But crossed curves mean that one person can have a better chance on easy items while another has a better chance on hard ones. If we allow that to happen, who shall we say is the more able?
Similarly, if we want to think that the probability of success on the harder of two items should always be less than the probability of success on the easier, no matter who attempts the items, if that is what we intend by "harder," then we must see to it that variation in item discrimination sufficient to produce item characteristic curves that cross does not occur.
The Impossibility of Estimating Item Discrimination Directly
There are computer programs that try to estimate values for an item discrimination parameter. But "the method usually does not converge properly" (Lord, 1968, p. 1015) and "experience has shown that if ... restraints are not imposed, the estimated value of [discrimination] is likely to increase without limit" (Lord, 1975, p. 14). The inevitability of this barrier to practice can be understood by thinking about what happens when the traditional approach to estimating item discrimination is modernized and carried to its logical conclusion.
Consider the matrix of ones and zeros that results from giving a set of items to a sample of persons. The unweighted marginal sums of this matrix, the person and item scores, are the ingredients for Rasch estimates of ability and difficulty and are the first approximations used with more complicated models. If a model allows some items to be better than others for bringing out person ability, it must somehow use the data in hand to weigh each item for its "betterness." If items are thought to vary in their capacity to discriminate among persons, this must express itself in the correlation between persons' responses to the items and estimates of the persons' abilities. One can compute these correlations, Ri, and, from them, item weights of the form wi = [Ri/(1-Ri)]^0.5. These weights would be extremely large and positive for Ri values close to +1, equal to zero when Ri=0 and extremely large and negative for Ri values close to -1.
As soon as these weights are calculated, however, the unweighted scores from which they were derived are no longer best for estimating person ability. In particular, the item with the largest Ri now has the largest wi and should have the most influence on ability estimates. Estimation should be improved by calculating weighted scores. But now the weights based on correlations with unweighted scores are also no longer best. So the weights are re-estimated by recalculating the correlations - now correlations between item responses and weighted person scores. The outcome is a new set of weights that require a new set of correlations, and so on.
The Ri that was largest gets larger until it overwhelms the weighted score and produces an Ri of one and a wi of infinity! If one tries to escape by avoiding the offending item (a paradox since, according to this strategy, it has just proven itself best), the item with the next largest correlation takes its place and so on.
One may have hoped that the seemingly reasonable weighting procedure described would converge to good estimates of "true" item discriminations. But it won't. Instead, as this example shows - and as is encountered when attempts are made to apply the "two" and "three" parameter models - estimates of item discrimination (unless restrained within arbitrary boundaries which cannot be estimated from the data) drift off to infinity one by one.
Item discrimination cannot be estimated directly or efficiently in the way Rasch item difficulty and person ability can. The best one can do is to "indicate" discrimination indirectly by first conditioning the data with Rasch estimates - estimates which are based on the assumption ["specification"] that item discriminations do not vary - and then using the Rasch residuals to "obtain some rough estimates of the [discriminations]" (Andersen, 1973,p. 135).
This situation need not lead to paralysis, however. No one believes the rulings on a ruler are identical in their capacity to discriminate lengths. It is sufficient that they are similar enough in width to be used as if they were identical. The practical problem of variation in item discrimination can be treated through "supervision" rather than estimation. If one lets the Rasch model govern the selection of items, one can work with discrimination as a supervised constant and then use the Rasch model to validate one's efforts and, where valid, to calibrate items and measure persons.
WHAT CAN BE DONE WITH THE RASCH MODEL
The Rasch model is so simple that its immediate relevance to contemporary measurement practice and its extensive possibilities for solving measurement problems may not be fully apparent. Those who base their measurement of persons or calibration of items on unweighted scores are already acting as though they were using the Rasch model without, perhaps, reaping the conveniences and opportunities that their practice can provide.
Item Fit Can be Evaluated by a Chi-Square Test
The conformity of any item and any sample of persons to the Rasch model, and even the conformity of any particular item and person can be evaluated explicitly by fitting the Rasch model to the data, calculating the residuals in the data from the values expected from the model, and examining these residuals. While a single unacceptable residual does not determine whether the main trouble lies in the person or in the item, this can be clarified when residuals are collected over persons for a given item. The magnitude of their mean square will indicate the extent to which the item is at fault (Wright and Panchapakesan 1969; Wright, Mead, and Draba, 1976; Mead, 1976).
Any item can be analyzed for bias with respect to the sex or culture of persons by calculating a regression of its residuals on indicators of these background variables. Since data from items that are found to be biased can be deleted from persons' responses without interfering with estimates of person ability, one can correct for item bias in a test without losing the information available from unbiased items.
Item Calibration Can Be Sample-Free
Once items have been validated by successful tests of fit to the Rasch model, they must be calibrated on the latent variable defined by the bank of "good" items under construction. The traditional index of item difficulty - proportion right in a calibrating sample - varies with sample ability distribution, e.g., high for very able samples, low for less able ones. To obtain a sample-free calibration, this sample-bound item score must be adjusted for the influence of sample ability.
Item score (the number of persons who got item i right) depends primarily on the number of persons N attempting the item, their mean ability M, an expansion factor Y = (1 + V/2.89)^0.5, which represents their ability variance V, and the difficulty di of the item. These four factors can be combined to approximate the item score si as:
si = N e[(M-di)/Yi]/{1 + e[(M-di)/Yi]} (14)
This expression can be solved for di to yield a Rasch difficulty estimate
di = M + Y ln[(N - si)/si] (15)
which illustrates the way the Rasch model adjusts sample-bound item scores for the influence of sample ability level and dispersion and so produces sample-free item difficulties. Thus item difficulty is estimated as equal to the mean ability of those sampled plus an adjustment for "sample spread" times the loge odds wrong answers to the item. While the proportion of wrong answers is sample-bound, the "sample spread" coefficient and the sample ability level correct this sample bound statistic, leaving an item difficulty estimate which is free from the influence of the ability mean and variance of the calibrating sample of persons. (The approximate expression shown adjusts item calibration only for the mean and variance of sample ability. In practice one can easily make an adjustment for the entire distribution of ability reflected in persons' observed scores. For examples see Wright, 1968, pp. 89-93; Wilmott and Fowles, 1974, pp. 25-33, pp. 64-78.)
Item Precision Can Be Determined From a Standard Error of Calibration
The Rasch model can be used to derive an estimate of the precision of each item calibration. This standard error of item difficulty depends strongly on how large the calibrating sample is and weakly on the relationship between item difficulty and the ability distribution of persons in the calibrating sample. It is well approximated by 2.5/N^0.5 logits {25/N^0.5 WITs}, where N is the calibration sample size. The value 2.5 is a compromise for an error coefficient that depends on the correspondence between item difficulty and the abilities of persons in the calibration sample. The correct value varies from 2, when the sample is entirely centered on the item, through 3, as the sample proportion of right answers goes below 15% or above 85% (Wright and Douglas, 1974a, pp. 16-18, p. 34).
This approximation is useful in the design of item calibration. If the precision with which the difficulties of items must be estimated can be specified, one can use 2.5/N^0.5 to determine the sample size necessary to achieve satisfactory calibrations, providing the abilities of the sample of persons selected are distributed within a logit or two of the item difficulty.
Satisfactory calibrations are those precise enough to protect measurements from unacceptable disturbance. Analysis shows that for tests of more than 20 or 30 items that are, "positioned" within a logit or two of the mean ability of the group with whom they will be used, calibration samples as small as 100 persons (producing standard errors of calibration of about .25 logits) are useful. And 400 persons (producing standard errors of calibration of about .12 logits) are almost always enough, not only to calculate items, but to evaluate their fit (Wright and Douglas, 1975a, pp. 35-39).
Item Banks Automatically Equate All Possible Tests
When items are constructed and administered so that their performance approximates the Rasch model, item difficulties that have been estimated from a variety of calibrating samples can be easily transformed onto a single common scale. The resulting set of commonly-calibrated items forms an item bank from which any subset of items can be drawn to make up a test (Choppin, 1968, 1974, 1976; Wilmott and Fowles, 1974, pp. 46-51). Because all the items share a common calibration, the measures implied by scores on all such tests are automatically equated and no further collection or analysis of data is needed. The vexing problem of test equating is solved, for all possible tests drawn from the bank, once and for all (Rentz and Bashaw, 1975, 1977). Good approximations for converting scores on a test of calibrated items into test-free measures and their standard errors are given under the heading "Person measurement can be test-free."
LINKING TESTS: The way a pair of tests is usually equated is by giving them together to a common sample of persons, and defining as equivalent scores that correspond to a common percentile rank. The items on a pair of tests that have already been administered to a common sample of persons can be calibrated onto a common Rasch scale simply by considering the pair as one long test. A more economical method of building a commonly-calibrated item bank, however, is to embed links of 10 to 20 common items in pairs of otherwise different tests. Each test can then be taken by a different sample of persons; no person need take more than one test. But all items in all tests can be commonly calibrated (i.e., equated) through a network of links.
Suppose two 60-item tests are to be equated by giving them together to a sample of 1200 persons - a likely plan, since precise estimation of score-percentiles is necessary for successful percentile equating. The same job can be done with half as much data by composing a third 60-item test, made up of 30 items from each of the original pair, and giving each of these three tests to a sample of 400 persons. Each of the 1200 persons thus takes only one test but all 120 items can be calibrated together through the two 30-item links that connect the three tests.
A pair of separate and independent estimates of difficulty are produced for each item that is common to a pair of tests. According to the Rasch model, the estimates in each pair are statistically equivalent except for a single constant of translation that is the same for all items in both tests. This makes estimation of the translation constant easy, and provides a way to estimate the goodness of the equating.
Suppose two tests, a and b, are joined by a common link of K items, that each test is given to its own sample of N persons, and that dia and dib are the estimated difficulties of item i in each test. The constant necessary to translate all item difficulties in the calibration of test b onto the scale of test a would be
tab = sum(dia-dib)/K i=1,K (16)
Each difficulty estimate would have a standard error of about 2.5/N^0.5 logits so that tab would have a standard error of about 3.5/(NK)^0.5 logits [35/(NK)^0.5 WITs].
The validity of this link can be judged by using the fit statistic sab² NK/12 [sab² NK/1200 for WITs], which has an approximately chi-square distribution with (K-1) degrees of freedom, where
sab² = sum(dia - dib -tab)² i=1,K (17)
The validity of any item in the link can be judged by using the statistic (dia - dib - tab)²N/12, which has an approximately chi-square distribution with one degree of freedom.
In deciding how to interpret these evaluations of fit, it should be kept in mind that random uncertainty in item difficulty of less than .2 or .3 logits has no practical bearing on person measurement (Wright and Douglas, 1975a, pp. 35-39). Samples of 400 persons and links of 10 good items are enough to keep link quality at better than .3 logits [3 WITs] or less.
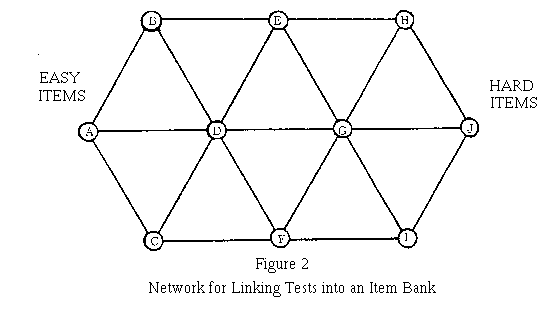
TEST NETWORKS: As the number and difficulty range of items to be introduced into an item bank grows beyond the capacity of any one person, it is necessary to develop an efficient linking system that distributes the items evenly over a network of interlinking tests. The Rasch model can be used to calibrate all these items on a common scale and to check the various estimated translations against one another for coherence (Doherty and Forster, 1976; Ingebo, 1976). Figure 2 is a picture of such a network. Each circle represents a test that is sufficiently narrow in its range of item difficulties to be manageable by a suitable sample of persons. Each line connecting two circles represents a link of common items that are shared by the two tests it joins. Tests increase in difficulty horizontally, and are of comparable difficulty vertically.
The hypothetical network shown in Figure 2 could connect ten 60-item tests through nineteen 10-item links to cover a total of 600 - 190 = 410 items. If 400 persons were administered each test, then 410 items could be evaluated and, where fitting, calibrated in such a way as to place all items on a common scale from the responses of only 4000 persons. Even 2000 persons, 200 per test, would provide estimates good enough to determine the possibility of building an item bank from the best of the 410 items.
The building blocks of this hypothetical network are the ten triangles of three tests each. If a triangle fits the Rasch model, its three translation constants should sum to within a standard error or two of zero. The standard error of such a sum is about 6/(NK)^0.5 logits [60/(NK)^0.5 WITs], where N is the number of persons used for the calibration of each test and K is the number of common items in each test pair. The success with which common item calibrations are achieved throughout the network can be evaluated by analyzing the magnitudes and directions of these triangle sums. Shaky regions can be identified and steps taken to isolate or improve them.
If success is realized, the outcome is a bank of commonly calibrated items far larger in number and far more dispersed in difficulty than any single person could cope with. Yet because of their common calibration, these items can be used to compose a prolific family of useful tests, long or short, easy or hard, widely spaced in item difficulty or narrowly focused, all automatically equated on a common scale.
Some Advantages of Item Banks
FLEXIBILITY: Not only nationally-used items, but items germane to the content of local curricula can be introduced together into the same banking system. Decisions on keeping or dropping items, whether nationally sanctioned or locally inspired, can be made on entirely objective grounds. If an item fits, it can be used. If not, its residuals can be examined for clues as to why it didn't work.
CRITERION REFERENCING: If there are milestone events that have special meaning to users of the bank-events such as high grades, honors, promotions, graduations or college admissions - then success in mastering these criteria can be scored dichotomously, Xni=1 for success and Xni=0 for failure, and introduced into the analysis along with performance on ordinary items. In this way each criterion can be calibrated onto the scale of the item bank just like an ordinary test item. Each college, for example, could be indexed as a separate criterion so that the differing scale values (difficulties) of admission to different colleges could be estimated and compared quantitatively. Those who want criterion referencing can use any items in the bank to measure any person's approach to, and departure from, any chosen milestone with whatever precision they are willing to spend items on.
DEFINING VARIABLES: The investigation of what kinds of items fit into a bank and what kinds do not makes possible a detailed analysis of a variable's operational definition. Any hypothesis about the nature of a variable which can be expressed in terms of observable events can be empirically investigated by attempting to calibrate these "challenge" events into the bank and observing how they fit and where their residuals depart from expectation.
STUDYING DEVELOPMENT: The quantitative study of development depends on the ability to make measurements over a wider range of difficulty values than can be covered with a single test. In order to capture the range of growth, one must be able to compare measures from tests so different in difficulty that no person could take them simultaneously. The quantitative study of mental development requires banks of commonly calibrated items from which equated tests of varying difficulty can be assembled.
NORM REFERENCING: While norms are no more fundamental to the calibration of item banks than are distributions of height to the ruling of yardsticks, it is usually useful to know the normative characteristics of a variable defined by an item bank. Because of a shift in emphasis, norming a variable takes less data than does norming a test. One need only use enough items to estimate the desired normative statistics. Once the variable is normed, all possible scores from all possible tests drawn from the bank are automatically norm referenced through the variable.
Usually it is sufficient to estimate the mean and standard deviation for each cell in a normative sampling plan. Those two statistics can be estimated from a random sample of 100 or so persons with a norming test of just two items. Of course a norming test of 10 to 15 items does a better job, but more than 15 items will seldom be necessary. It is possible to norm 6 different variables simultaneously by allotting 10 items to each of them in one 60-item test. For example, one could obtain norms for reading comprehension, language skills, math, science, information retrieval and social studies all at one sitting.
A procedure for estimating the mean and standard deviation for any cell in a sampling plan is as follows:
1. Select from the item bank a norming test of K items that are sufficiently dispersed in difficulty di to cover the expected ability dispersion of persons in that cell (for more details see the section on Best Test Design below).
2. Administer this test to a random sample of N persons drawn from the cell.
3. Observe the number of persons si who succeed on each item.
4. Calculate the natural loge odds right answers for each item, hi = ln[si/(N - si)] i=1,K (18)
5. Regress these loge odds hi on item difficulty di over the K items to obtain the intercept a and slope c of the least squares straight line.
6. Estimate the mean M and the standard deviation S of abilities in that cell as,
M = -a/c (19)
S = 1.7[(1 - c²)/c²]^0.5 (20)
[This method is based on the relation
di = M - (1 + S²/1.7²)^0.5 hi (21)
developed in Wright and Douglas (1975a, pp. 24-25: 1975b, pp. 25-29).]
CONTINUOUS QUALITY CONTROL: One cannot expect the items in a bank to retain their calibrations indefinitely or to work equally well for every person with whom they may someday be used. The difficulty level of an item can be influenced, for example, by changes in curricula and by differences in cultural background. Item calibration and item fit should be supervised continuously. This can be done by routinely examining observed residuals from expectation at each administration of each item. An occasional surprising residual suggests an anomalous testing situation or a peculiar person. Tendencies for items to run into trouble, to shift difficulty or to be biased for some types of persons can be discovered through a cumulative analysis of residuals over time, place and type of person. Problematic items can be removed from use, brought up to date in difficulty, or used with a correction for bias.
Person Measurement Can be Test-Free
When two persons earn exactly the same score on a test, their test performances are generally viewed as equivalent regardless of the particular items each person answers correctly. If identical scores are viewed as equivalent measures, then one does not care which items produce a score and "item-free" measurement is being used. The Rasch model shows how this widespread practice of item-free measurement within a test leads, without any additional assumptions ["specifications"], to test-free measurement within a bank of calibrated items.
This is done by adjusting for between-test differences in item difficulty, so that what is left is a test-free person measure on the scale defined by the bank calibrations. Person score depends primarily on the number of items L in the test, their mean difficulty level H, an expansion factor X = (1 + U/2.89)^0.5, which represents their difficulty variance U, and the ability br of a person who earns a score of r. These four factors can be combined to approximate the person score,
r = L e(br-H)/X /{ 1 + e(br-H)/X} (22)
This expression can be solved for br to yield a Rasch ability estimate
br = H + X ln[r/(L - r)] (23)
which shows how the Rasch model adjusts test-bound person scores for test difficulty level and spread to produce test-free person measures. To estimate the standard errors of these measures, one can use
SE(br) = X[L/r(L- r)]^0.5 (24)
(For examples see Wright, 1968, p. 95; Wilmott and Fowles, 1974, pp. 34-38.)
Measurement Quality Can be Evaluated by a Chi-Square Test of Person Fit
When examinees take a test one cannot be sure they will work as intended. One can only arrange the testing situation so as to promote comfort with the test, provide practice at its mechanics, allow enough time so that slowness does not affect performance, choose items relevant to the persons' ability level and provide motivation so that they will not guess or sleep but will work with all their ability on the answer to every item. In spite of every effort, however, it is clear that some persons under some circumstances will render flawed performances.
GUESSING, SLEEPING, FUMBLING. AND PLODDING: When test scores are influenced by guessing. sleeping, practice or speed, it would be desirable to detect these influences and, where possible, to correct for them. If guessing on difficult items or sleeping on easy ones influences persons' responses, then regressing their response residuals on item difficulty will bring that out.
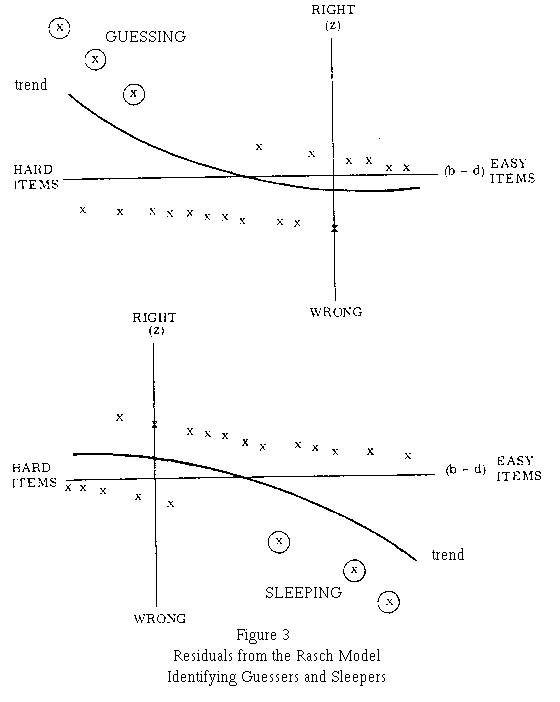
Figure 3 shows the trend of residuals for typical "guessers" and "sleepers". The residual z = (x - P)/[P(1-P)]^0.5, or -e(b-d)/2 for x = 0 and +e-(b-d)/2 for x = 1, has been plotted against the estimated differences between person ability and item difficulty (b-d). Items increase in easiness toward the right. Guessers and sleepers can be distinguished by the quadratic regression of their residuals on item difficulty. This regression will be curved up for guessers and down for sleepers.
If lack of practice affects early items or lack of speed affects late ones, regressing an individual's residuals on item position will bring that out. "Fumblers" who get off to a bad start and "plodders" who never get to the last items can be distinguished by the linear regression of their residuals on item position; it will be positive for fumblers and negative for plodders.
These analyses are available for each person. It is not necessary to assume that everyone - or that no one - guesses, sleeps, fumbles or plods. Those possibilities can be evaluated on an individual basis and each person's responses can be edited to remove or correct whatever disturbances are found.
ITEM BIAS: Another source of person misfit is item bias. Some items may be couched in terms that are unfamiliar to some persons, terms which do not bear directly on the ability to be measured. If a math item depends on a high reading level, then among poor readers, the item will be biased against the expression of math ability. If a reading item depends on special vocabulary that is familiar to some but strange to others, the item will be biased against the expression of reading ability among the unexposed. Rasch residuals make the statistical detection of item bias possible and provide an objective quantitative basis for eliminating or correcting it (Wright, Mead, and Draba, 1976).
PERSON DIAGNOSIS: Item residuals can also be used for person diagnosis. An improbable residual identifies a person for whom the item is miscalibrated. If experience has shown the item to be generally "fair", then an excessive residual suggests an irregularity in the person's development.
Measurement Precision Can be Determined from the Standard Error of Measurement
The precision of measurement of particular persons based on their performance on a particular set of items, possibly chosen to measure them best, depends upon how many items the persons take, how relevant these items are to their ability, and how well the items were calibrated. Item difficulties are ordinarily so well estimated in Rasch measurement that little is lost by acting as though item difficulties are known. When a test is within a logit of the person to be measured, item relevance plays only a minor role. Usually the standard error of measurement can be well-approximated by 2.5/L^0.5 logits [25/L^0.5 WITs], where L is the number of items taken and 2.5 is the compromise value for the test "relevance" coefficient discussed earlier (Wright and Douglas, 1975a, pp. 16-18, 34).
Unlike the standard error of a score - which has the preposterous characteristic of becoming zero at scores of zero or 100%, where the estimation of person ability is infinitely imprecise - the Rasch standard error is smallest for measures derived from central scores (where information about the ability of the person is maximum) and infinite at the extremes of zero and 100%.
Best Test Design Becomes Simple
With an item bank to draw upon and an explicit model to specify how a person and an item are supposed to interact, it becomes easy to design and construct the best possible test for any measurement situation (Wright and Douglas, 1975a, pp. 1-18). To do this the ability distribution of the persons to be measured (the target) is anticipated as well as possible on the basis of whatever information is available. Both theory and prior experience are used to form a guess as to where the target is located and how much it spreads out around that point. A distribution of item difficulties is chosen to match this target specification. The number of items to be used is set so that the test reaches a degree of precision sufficient to make the measurement worthwhile.
The innumerable possibilities for target distributions and test shapes can be satisfactorily accommodated by the following simple procedure (Wright and Douglas, 1975a, pp. 26-31):
To construct a best test;
1. Guess target location (mean ability, M) and dispersion (standard deviation of ability, S) as well as possible. If outer boundaries are used to specify the target's location and dispersion, relate them to M and S by letting the lower boundary define M-2S and the upper boundary define M+2S.
2. Design a test with item difficulties centered at M and spread evenly over the range M-2S to M+2S, with enough items in between to produce a test length of L = 6/SEM², where SEM is the desired standard error of measurement in logits [L=600/SEM² for WITs].
3. Select from the item bank the best available items to fulfill this design, and use the range and mean of the obtained item difficulties to describe the "height" h and "width" w of the resulting test (Wright and Douglas, 1975a, pp. 32-35).
Not only is this test as good for all practical purposes as any other test of equal length which might be constructed, but its use as an instrument of measurement is simple. One all-purpose table of within-test measures xfw for relative scores of f = r/L on tests of width w and height h can be used to convert any scores r on all such tests into test-free measures of person ability br through the relation bf = h + xfw. Standard errors of measurement can be approximated by 2.5/L^0.5 or can be looked up in a companion table. No further calculations are ever needed to convert a test-bound score to a test-free measure (Wright and Douglas, 1976a, pp. 33-34).
As an example of test design, suppose it is desired to remeasure a pupil whose last measure was 74 WITs with a standard error of measurement SEM of 4 and it is thought that the pupil has grown at least 5 but not more than 15 WIT since the last measurement. Using an error allowance of two SEMs, or 8, around 74, this information defines a target running from no less than 74 - 8 + 5 = 71 to no more than 74 + 8 + 15, 97. A best test for this target would be one with items spread evenly in difficulty from 71 to 97 WITs.
The number of items needed will depend on the desired precision of measurement. If the pupil's new measure is also to have an SEM = 4, then L = 600/42 = 38 items will do. But if it is desired to detect growth of at least 10 WITs with 95 percent confidence, enough items must be used to make the standard error of the difference SED between 74 and 84 no more than 5. Since SED² = SEM1² + SEM2², then SEM2² = 5² - 4² = 9 and L = 600/9 = 67 items will be required.
Tailored Testing Becomes Easily Manageable
The construction of a bank of Rasch calibrated items makes the efficient pencil-and-paper implementation of tailored-testing simple. The relative uniformity of measurement precision within a logit of the center of tests of typical difficulty dispersion shows that it is only necessary to bring the bulk of the items to within a logit of their intended target for optimal tailoring. This may be done in various ways:
GRADE-PLACEMENT TAILORING: In many situations grade-placement tailoring will be satisfactory. Prior knowledge of the approximate grade placement of the target group or child and of the variable's grade norms can be used to determine an appropriate [Wright prefers "useful"] segment of items in a bank. Normative data from tests on a variety of school subjects suggest that typical within-grade standard deviations are about one logit. When this is so, even a rough estimate of a pupil's within-grade quartile provides enough information to design a best test for that pupil.
PILOT-TEST TAILORING: If grade placement tailoring is not practical, then tailoring can be accomplished with a pilot test of 5 to 10 items that are spread out enough in difficulty to cover the most extreme target expected. If the pilot test is set up to be self-scoring then, after scoring themselves, examinees can use their number right score to guide themselves into a second test of 40 to 50 items which is tailored to the ability level implied by their pilot test score (Forbes, 1976).
SELF-TAILORING: A third, even more individualized, scheme may be practical in some circumstances. The person to be measured is given a booklet of 100 or so items arranged in uniformly increasing difficulty and asked to find their own best working level. Testing begins when the examinee finds items that are hard enough to provide a challenge but easy enough to afford a reasonable chance of success. The examinee works ahead into more difficult items, until either time is up or the level of difficulty becomes too great. If time remains, the examinee goes back to the first item attempted and works backward into easier items until time is up or boredom overcomes incentive. The self-tailored test on which this person is measured is the continuous segment of items from the easiest through the most difficult attempted.
This paper-and-pencil approach is self-adapting to individual variations in speed, test comfort and level of productive challenge. The large variety of different test segments which can result are easy to handle. The sequence number of the easiest and hardest items attempted, and the number correct can be read off a self-scoring answer form. These values can be converted into a measure and its standard error merely by using a simple one page table made to fit into the booklet of items and based on their calibrations on the general scale which defines the latent variable under consideration.
CONCLUSION
The Rasch model is a supposition about what happens when a person responds to an item. It defines the supposed causes of the response, directs how these causes can be estimated and allows determination of how well its supposition fits the situation. Unweighted scores are appropriate ["useful"] for person measurement if and only if what happens when a person responds to an item can be usefully approximated by the Rasch model. No other latent trait model provides a sufficient or consistent estimator for person ability which is, as a true estimator must be, entirely a function of observable data. Ironically, for anyone who claims skepticism about "the assumptions" of the Rasch model, those who use unweighted scores are, however unwittingly, counting on the Rasch model to see them through. Whether this is useful in practice is a question not for more theorizing, but for empirical study.
BENJAMIN D. WRIGHT
MESA Research Memorandum Number 42
MESA PSYCHOMETRIC LABORATORY
REFERENCES
ANDERSEN, E. B. Asymptotic properties of conditional maximum likelihood estimators CMLE, Journal of the Royal Statistical Society. 1970, 32, 283-301.
ANDERSEN, E. B. The numerical solution of a set of conditional estimation equations. The Journal of the Royal Statistical Society: Series I, 1972, 34 (1), 42-54.
ANDERSEN, E. B. A goodness of fit test for the Rasch model. Psychometrika, 1973, 38 (1), 123-140.
ANDRICH, D. The Rasch multiplicative binomial model: Applications to attitude data. Research Report No. 1, Measurement and Statistics Laboratory, Department of Education, University of Western Australia, 1975.
CHOPPIN, B. An item bank using sample-free calibration. Nature, 1968, 219 (5156), 870-872.
CHOPPIN, B. The introduction of new science curricula in England and Wales. Comparative Education Review, 1974, 18, No. 2.
CHOPPIN, B. Recent developments in item banking. In Advances in Psychological and Educational Measurement. New York: Wiley, 1976.
COHEN, L. A modified logistic response model for item analysis. Unpublished manuscript, 1976.
CONNOLLY, A. J., NACHTMAN, W., & PRITCHETT, E. M. Keymath: Diagnostic Arithmetic Test. Circle Pines, Minn.: American Guidance Service, 1971.
DOHERTY, V. W. & FORSTER, F. Can Rasch scaled scores be predicted from a calibrated item pool? Paper presented to American Educational Research Association, San Francisco, 1976.
FORBES, D. W. The use of Rasch logistic scaling procedures in the development of short multi-level arithmetic achievement tests for public school measurement. Paper presented to American Educational Research Association, San Francisco, 1976.
INGEBO, G. How to link tests to form an item pool. Paper presented to American Educational Research Association, San Francisco, 1976.
LORD, F. M. An analysis of the Verbal Scholastic Aptitude Test using Birnbaum's three-parameter logistic model. Educational and Psychological Measurement, 1968, 28, 989-1020.
LORD, F. M. Evaluation with artificial data of a procedure for estimating ability and item characteristic curve parameters. Research Bulletin 75-33. Princeton, N.J.: Educational Testing Service, 1975.
MEAD, R. L. Assessing the fit of data to the Rasch model through analysis of residuals. Doctoral dissertation, University of Chicago, 1976.
RASCH, G. Probabilistic models for some intelligence and attainment tests. Copenhagen, Denmark: Danmarks Paedogogiske Institut, 1960.
RASCH, G. An individualistic approach to item analysis. In P. F. Lazarsfeld and N. W. Henry (Eds.), Readings in Mathematical Social Science. Chicago: Science Research Associates, 1966, 89-108. (a)
RASCH, G. An item analysis which takes individual differences into account. British Journal of Mathematical and Statistical Psychology, 1966, 19 (1), 49-57. (b)
RASCH, G. A mathematical theory of objectivity and its consequences for model construction. Report from European Meeting on Statistics, Econometrics and Management Sciences, Amsterdam, P.168.
RENTZ, R. R. & BASHAW, W. L. Equating reading tests with the Rasch model. Athens, Georgia: Educational Resource Laboratory, 1975.
RENTZ, R. R. & BASHAW, W. L. The national reference scale for reading: An application of the Rasch model. Journal of Educational Measurement, 1977, 14, 161-180:
WILMOTT, A. & FOWLES, D. The objective interpretation of test performance: The Rasch model applied. Atlantic Highlands, N.J. NFER Publishing Co., Ltd., 1974.
WOODCOCK, R. W. Woodcock Reading Mastery Tests. Circle Pines, Minnesota: American Guidance Service, 1974.
WRIGHT, B. D. Sample-free test calibration and person measurement. In Proceedings of the 1967 Invitational Conference on Testing Problems. Princeton, N.J.: Educational Testing Service, 1968, 85-101.
WRIGHT, B. D. & DOUGLAS, G. A. Best test design and self-tailored testing. Research Memorandum No. 19, Statistical Laboratory, Department of Education, University of Chicago, 1975. (a)
WRIGHT, B. D. & DOUGLAS, G. A. Better procedures for sample-free item analysis. Research Memorandum No. 20, Statistical Laboratory,, Department of Education, University of Chicago, 1975. (b)
WRIGHT, B. D. & DOUGLAS, G. A. Rasch item analysis by hand. Research Memorandum No. 21, Statistical Laboratory, Department of Education, University of Chicago, 1976.
WRIGHT, B. D. & DOUGLAS, G. A. Best procedures for sample-free item analysis. Applied Psychological Measurement, Winter, 1977. (a)
WRIGHT, B. D. & DOUGLAS, G. A. Conditional (CMLE) versus unconditional (JMLE) procedures for sample-free item analysis. Educational and Psychological Measurement, Spring, 1977. (b)
WRIGHT, B. D. & MEAD, R. I. CALFIT: Sample-free calibration with a Rasch measurement model. Research Memorandum No. 18, Statistical Laboratory, Department of Education, University of Chicago, 1975.
WRIGHT, B. D. & MEAD, R. J. BICAL: Calibrating items and scales with the Rasch model. Research Memorandum No. 23, Statistical Laboratory, Department of Education, University of Chicago, 1977.
WRIGHT, B. D., MEAD, R. J. & DRABA, R. Detecting and correcting test item bias with a logistic response model. Research Memorandum No. 22, Statistical Laboratory, Department of Education, University of Chicago, 1976.
WRIGHT, B. D. & PANCHAPAKESAN, N. A procedure for sample-free item analysis. Educational and Psychological Measurement, 1969, 29. 23-48.
AUTHOR
WRIGHT, BENJAMIN D. Address: 5721 Harper Avenue, Chicago, IL 60637. Title: Professor. Degrees: B.S. Cornell University, Certificate. Chicago Institute for Psychoanalysis, Ph.D. University of Chicago. Specialization: Psychoanalytic Psychology; Psychometric Theory; Research Methods.
This appeared in
Journal of Educational Measurement 14 (2) pp. 97-116, Summer
1977
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Apr. 21 - 22, 2025, Mon.-Tue. | International Objective Measurement Workshop (IOMW) - Boulder, CO, www.iomw.net |
| Jan. 17 - Feb. 21, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Feb. - June, 2025 | On-line course: Introduction to Classical Test and Rasch Measurement Theories (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| Feb. - June, 2025 | On-line course: Advanced Course in Rasch Measurement Theory (D. Andrich, I. Marais, RUMM2030), University of Western Australia |
| May 16 - June 20, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 20 - July 18, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Facets), www.statistics.com |
| July 21 - 23, 2025, Mon.-Wed. | Pacific Rim Objective Measurement Symposium (PROMS) 2025, www.proms2025.com |
| Oct. 3 - Nov. 7, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo42.htm