In this paper, we discuss curricular implications of item banking and its practical value to teachers and students, and list a variety of working banks with their sources. We also review the psychometric basis of item banking, outline a family of computer programs for accomplishing banking, and give the equations necessary to build a bank. We conclude with a discussion of item quality control and examples of items that misfit because of miskeying, guessing, or carelessness.
WHAT ITEM BANKS ARE
Some use "item bank" to refer to any collection of items. But a bank of carefully calibrated test items is more than a collection (Choppin, 1968, 1976, 1978, 1981. Bruce Howard Choppin, who died in Chile on July 15, 1983, was one of the earliest and most persistent item bankers. He was our student, colleague and friend. May his pioneering work be long appreciated). It is a composition of coordinated questions that develop, define, and quantify a common theme and thus provide an operational definition of a variable.
When an item bank is used to measure educational achievement, it can represent a strand of a school curriculum. Its calibrated items can provide a systematic specification of what is important. It may seem strange to think of item banks as defining curricula. But a curriculum can be visualized as a family of learning strands, each represented as a hierarchy of tasks from elementary to advanced. Test items written to probe tasks representing a particular curriculum strand should reproduce in their observed calibrations the ordering of the curriculum hierarchy. When the empirical ordering is valid, then the item calibrations provide a curriculum map from which teaching strategies can be designed and against which rates of learning can be calculated. Table 1 lists some examples of this kind of curriculum mapping (Connolly, Nachtman, & Pritchett, 1971; Cornish & Wines, 1977; Elliott, 1983; Izard, Farish, Wilson, Ward, & Van der Werf, 1983; Koslin, Koslin, Zeno, & Wainer, 1977; Rentz & Bashaw, 1977; Stone & Wright, 1981; Woodcock, 1973).
| TABLE 1 Some Item Banks | ||||
|---|---|---|---|---|
| Key | Topic | Items | Target | Use |
| NBME NBME NBME NWEA NWEA NWEA DETR DETR DETR GLEN GLEN HOUS HOUS NRS IBSM WRMT BAS RAPT DRPT KMTH MAPS KCT |
I-medical science II-clinical science III-clinical competence mathematics language arts reading mathematics reading writing reading language arts mathematics reading reading mathematics reading 21 basic abilities mathematics reading mathematics mathematics short term memory |
9452 8629 6865 1587 1184 1080 2200 2100 500 500 500 432 272 2644 1497 800 588 552 329 210 188 51 |
2nd year med 4th year med 1st year res grades K-12 grades K-12 grades K-12 grades 1-8 grades 1-8 grades 6-8 elementary elementary grades 7-9 grades 7-9 grades 3-7 elem/secon grades K-12 years 3-17 elementary grades 3-12 grades K-6 elementary years 3-80 |
18000/year 15000/year 13000/year 500 school districts city-wide city-wide city-wide county-wide county-wide city-wide city-wide U.S. Scotland U.S. England Australia U.S. U.S. Australia U.S. |
| NBME: NWEA: DETR: GLEN: HOUS: NRS: IBSM: WRMT: BAS: RAPT: DRPT: KMTH: MAPS: KCT: |
National Board of Medical Examiners, 3930 Chestnut,
Phila., PA 19104 Northwest Evaluation Association, 1410 South 200th, Seattle,WA 98146 Detroit Public Schools,Dept. of Research and Eval., Detroit,MI 48202 School District No. 12, Adams County, Northglenn, Colorado 80233 Houston Independent School District, Houston, Texas National Reference Scale. Ed. Res. Lab., Univ. Georgia, Athens 30602 Item Banking Secondary Math. Moray House Col. Educ. Edinburgh EH8 8AQ Woodcock Reading Mastery Test. Am.Guid.Serv., Circle Pines, MN 55014 British Ability Scales.Dept.Ed., Manchester Univ., Manchester M13 9PL Review and Progress Tests.Australian Cncl.Ed.Res.Hawthorn,Vict. 3122 Degrees of Reading Power Test. College Board, 888 7th, NYC, NY 10019 Key Math. American Guidance Service, Circle Pines, Minnesota 55014 Mathematics Profile Series.Aust.Cncl.Ed.Res. Hawthorn, Victoria 3122 Knox's Cube Test. MESA, Dept. Educ., Univ. Chicago, Chicago,IL 60637 |
|||
The first step toward an item bank is to outline the curriculum strand to be represented by the items. For this, it is wise to involve those who will use the bank. They know best which items are decisive for their curriculum and which are unimportant. A careful specification of the desired line of inquiry is essential. The consequent deliberations clarify for everyone how the curriculum strand that the bank is intended to represent will be defined by test items.
It is particularly important to specify ahead of time how items are expected to be ordered in difficulty. This provides a conceptual frame of reference for judging the validity and utility of the empirical ordering subsequently derived from student performance.
The measurement model used to build an item bank is an accounting system that constructs an empirical frame of reference for describing the curriculum strand. When each item is written to represent an element of the strand at a particular point on the achievement variable, then each item exemplifies the knowledge, skill, and behavior that defines achievement at that point. The calibration that becomes attached to each item puts this definition of the strand on an underlying continuum. Items with low calibrations describe easy tasks that define the elementary end of the strand. Items with high calibrations describe difficult tasks that define the advanced end of the strand. The progression through the items in the order of their calibrations from easy to hard describes the path that most students follow as they learn.
Item calibrations are obtained by applying a probabilistic model for what ought to happen when a student attempts an item (Rasch, 1960/ 1980). The probabilities allow for give and take between what is intended and what occurs. This is necessary because some students do not follow the expected path. The model tries to impose an orderly response process on the data. Evaluation of the extent to which the data can be understood and used in this way is an essential part of item banking.
To develop confidence in the structure of the bank, it is necessary to assess the extent of agreement among student performances and between student performances and teacher expectations. If there is much disagreement among students as to which items are hard and which are easy, then there may not be a common basis for describing progress. It may become impossible to say that one student has achieved more than another or that a student's change in position on the bank variable indicates development. If the empirical ordering of the items surprises the teachers who designed the bank, then they may not understand what their items measure. Fortunately, students tend to agree with one another and with their teachers on the relative difficulty of most test items so that item banking usually succeeds.
Reviewing the bank arrangement of items from easy to hard promotes a new kind of communication about the strands a curriculum contains and what can be done to teach them. This is a kind of communication that does not occur when off-the-cuff tests are patched together by teachers or off-the-shelf tests are brought in by publishers. When teachers review together the confirmations and contradictions that emerge as they compare the observed item hierarchy in an item bank with their intended one, they discover details and teaching sequences that they were unaware they shared with one another.
WHY ITEM BANKS ARE USEFUL
Implications for the Teacher
A well constructed item bank can provide the basis for designing the best possible test for every purpose. This is because it is not necessary for every student to take the same test in order to be able to compare results. Students can take the selections of bank items most appropriate to their levels of development. The number of items, their level and range of difficulty, and their type and content can be determined for each student individually, without losing the comparability provided by standardized tests. Comparability is maintained because any test formed from bank items, on which a student manifests a valid pattern of performance, is automatically equated, through the calibration of its items onto the bank, to every other test that has been or might be so formed.
A well organized item bank enables teachers to construct a wide variety of tests. They need not settle for standard grade level tests or administer the same test to every student in a class, school, or district. They can consider who is to be measured and for what purpose and select items accordingly. They can tailor each test to their immediate educational objectives without losing contact with the common core of bank items. They can write, bank and use new items that reflect their own educational goals while retaining, when their new items fit the bank, the opportunity to make whatever general comparisons they may require.
Items of wide ranging difficulty can be drawn from the bank to construct the survey tests needed for district assessment. Items detailed to specific purposes can be selected to make the criterion-referenced measurements needed for curriculum planning, individual placement, program admission, and certification.
Performance diagnosis is an especially useful by-product of tests tailored to teacher specifications and student status. Some fear that the best items for measuring achievement will not be good for diagnostic testing. But diagnosis relies on weighing discrepancies between observations and expectations. Weighing requires a metric. Expectations require a frame of reference. The best items for measuring are bound to become the best items for diagnosing because they are the items that best share a metric in an explicit frame of reference against which diagnostic discrepancies can be identified and weighed.
Psychometric Implications
Item banks return the development and control of testing to the local level without loss of comparability. The quantitative basis for objective comparisons among performances of students or between performances of the same student at different times is achieved through the itemization of the curriculum strand defined by the bank. This requires nothing more in item quality or relevance than is already taken for granted in most fixed-item, norm-referenced tests.
When items that share a common content are calibrated onto a common variable, each item represents a position on the variable that is also represented by other items of comparable difficulty. This makes it possible to infer a student's mastery with respect to the basic variable that the items share regardless of which items are administered or whom else has been tested. The idea that items might be exchangeable with respect to their contribution to a measure and hence to a general idea as to how much of a particular curriculum strand a particular student has learned may seem surprising. But this idea is a basic requirement of any measuring system in which many responses are collected but only one score is reported, including all of the fixed-item norm- referenced tests so widely used. It is the isolation of this exchangeable part of each item by its calibration on the common curriculum strand which frees the item's unique content for diagnostic use.
The summary information about a tested student should begin with the validity of the student's pattern of performance (Smith, 1982, 1984; Wright & Stone, 1979, chaps. 4 & 7). If the performance pattern is valid, then the measure estimates the student's level of mastery in terms of all the items that define the bank rather than merely the few items taken. This provides a criterion reference for the student's performance which is as detailed as the items in the bank and as broad as their implications.
The student's position on the variable also places that student among whomever else has ever taken items from the bank, rather than merely among those who have taken the same items. This provides a norm reference for the student's performance with respect to every other student who has produced a valid test performance with items from the bank.
Because items can be written, administered, and scored locally and because, when items are plentiful, there is no need for item secrecy, it becomes possible to analyze, report, and use the individual interactions between student and item immediately in the teaching-learning process. The calibration of the items facilitates this analysis because it enables an immediate evaluation of the consistency of each response. This focuses the teacher's attention on the particular responses that are most pertinent to a particular student's education. The teacher can go beyond the criterion and norm referencing produced by a student's position on the curriculum strand into an itemized diagnosis of the details of each student's particular performance.
Curricular Implications
An item bank can accept new items without large scale pretests. All that is needed is an analysis of the extent to which the pattern of student responses elicited by each new item is consistent with these students' estimated positions on the curriculum strand. New items that share the common content can be added as the curriculum develops. When these new items are administered with items already in the bank, their consistency with the bank can be evaluated au courant and, if satisfactory, the new items can be calibrated onto the bank and used immediately. This means that the contents of the bank can follow the curriculum strand as it develops. Freed from the constraint of a fixed list of items that must be administered as a complete set, teachers can teach to their curriculum. Then they can use their curriculum strand banks dynamically not only to assess how well their teaching is succeeding with individual students but also to build objective maps of the direction their curriculum is taking.
Test results, however individualized, are not restricted to single teachers' assessments of their own teaching methods. Because all of the items drawn from a particular bank are calibrated onto one common scale, teachers can compare their test results with one another, even when their tests contain no common items. This opportunity to compare results quantitatively enables teachers to examine how the same topic is learned by different students working with different teachers and hence to evaluate alternative teaching strategies. With common curriculum strands as the frames of reference, it becomes possible to recognize subtle differences in the way school subjects are mastered. The investigation of which teaching methods are most effective in which circumstances can become an ongoing, routine part of the educational process. Tests constructed from item banks can promote an exchange of ideas, not only about assessment, but also about curricula. The organization of curricular content provided by item bank calibrations can also supply an objective basis for the development and revision of curricular theory.
Implications for the Student
To be useful an educational measuring system needs items that can be made appropriate for measuring many students under many circumstances. But students sometimes guess, sometimes make careless errors when tired or rushed, sometimes misunderstand instructions, and sometimes possess special experience that interacts with some items. Factors like these can make some students' scores misleading. A careful analysis of the consistency of each student's pattern of responses on every testing is needed to guard against this.
When a student is asked to try an item, the intention is that the student's answer should express the difference between the student's ability and the item's difficulty. The simple logistic model (Rasch, 1960; Wright, 1968,1977) for the interaction between student and item explicitly excludes parameters for any process other than the one intended. As a result, the analysis of residuals from this model provides a strong framework for detecting individual disturbances (Ludlow, 1983; Smith, 1982, 1984; Wright & Stone, 1979, chaps. 4 & 7). When disturbances are detected, the teacher can investigate their source and make an informed decision about the most constructive reaction, not only for obtaining a better indication of the student's ability, but also for helping the student to deal with the cause of the disturbances. The testing session can be repeated with a comparable set of items under better conditions, if that is called for. Items too easy, too difficult, or inappropriate in some other way can be disqualified from scoring and a new measure estimated from the subscore on the "relevant" items remaining. The wisest reaction will depend on the reason for testing and on what has disturbed the testing session. Routine analysis of student performance consistency can help teachers make the best choice by calling performance problems to their attention and suggesting their nature.
HOW TO BUILD AN ITEM BANK
An item bank begins with a pool of items dominated in their content by a common curriculum strand. The flow chart in Figure 1 outlines the basic steps necessary to build an item pool into a bank. These steps will be described as a family of computer programs. Several studies explain the calibration and measuring algorithms (Englehard & Osberg, 1983; Wright & Panchapakesan, 1969; Wright & Stone, 1979). The bank building equations are given in this article. Table 1 lists some sites where computer programs like this have been used.
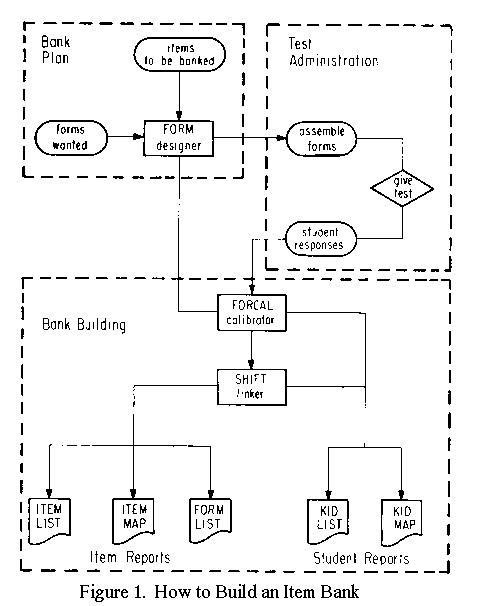
Designing Test Forms
Program FORM is used to distribute items among test forms so that there is a web of common item connections which maximizes the statistical strength of the linking structure, while meeting the practical requirements of the testing situation (Wright & Stone, 1979, chap. 5).
FORM reads the number of items to be calibrated, the number of items desired per form, the number of items desired per link, the expected difficulty of each item, and whether the pattern of form difficulties is to be parallel or sequential. FORM determines the number of links per form, total number of links, and total number of forms necessary for an optimal web.
FORM constructs a file of item specifications from which the banking system works; lists items by identification number, item name, link number, expected difficulty, correct response, and associated forms so that item test form placements can be checked; and lists items by form in their within form position to facilitate the verification of content coherence and form assembly.
Calibrating Test Forms
When forms are designed, assembled, and administered, student responses are recorded and filed in a student record that includes student identification, form taken, and item response string. This student file, sorted by form, is the form calibration input. Program FORCAL is used to take the item file produced by FORM and the student file prepared from testing, to calibrate items within each form, and to analyze within form item and student fit.
FORCAL estimates sample-free item difficulties from the sample-dependent item scores and the observed distribution of student scores. FORCAL also estimates within form student abilities, their standard errors, and student response pattern fit statistics. All students are measured and all items are calibrated at this stage, but the abilities and difficulties are still relative to the local origin defined by each form. Connections across forms cannot be made until a link analysis has equated all forms to a single common scale.
Analyzing Fit
The first estimation of item and form difficulties is based on all data and the expectation that these data can be used to approximate additive conjoint measurement (Broaden, 1977; Wright & Masters, 1982, chap. 1). The estimates of item and form difficulties are sample-free to the extent of this approximation. The empirical criterion is the degree of consistency between observation and expectation and the extent to which provocative subdivisions of data, by ability group, grade level, sex, and so on, produce statistically equivalent item and form calibrations (Ludlow, 1983; Mead, 1975).
Item-Within-Form Fit Analysis
The first check as to whether item difficulties are approximately sample-free is done during form calibration. If item estimates are invariant with respect to student abilities, student sample subdivisions will give statistically equivalent item difficulties.
One way to test this is to divide the student sample into subgroups by raw score r (the sufficient statistic for ability) and to compare the observed successes on each item i in each ability subgroup g with the number predicted for that subgroup. If parameter estimates are adequate for describing group g, then the observed number correct in group g will be near the estimated model expectation
Rgi = sum (Nyrpri) r in g ( 1 )
with estimated model variance
Sgi² = sum(Nrpri[1-pri]) r in g (2)
where Nr is the number of students with score r, and pri is the estimated probability of success for a student with score r on item i (Rasch, 1960). If observed and expected are comparable, given the model variance of the observed, then there is no evidence against the conclusion that subgroups concur on the estimated difficulty, and the confidence to be placed in this estimate can be specified with its modeled standard error. Similar analyses can be done for student subgroups defined in other ways.
Another way to check within form item fit is to evaluate the agreement between the variable manifested by item i and the variable defined by the other items. A useful statistic for this is a mean square in which the standard squared residual of observation x from its expectation p, zni² = (x- p)²/[p(1-p)], for each student n's response to item i, is weighted by the information in the observation, uni = p(1-p), and summed over N students.
Vi = {sum[zni²uni] / sum(uni)}{N/(n-1)} n=1,N (3)
This statistic is useful because it is robust with respect to idiosyncratic outliers. An alternative that detects outliers is the unweighted mean square, sum[z²/(N-1)]. When data fit the model, these statistics approximate one with variance about 2/(N - 1).
Calculating Test Form Links
When items have been calibrated within forms, there are as many difficulty estimates for each item as there are forms in which it appears. The items that appear in more than one form provide the linking data. Program SHIFT uses the differences observed between within form item calibrations and the bank requirement that each item be characterized by a single difficulty, regardless of form or sample, to estimate the relative difficulty of each form. This form difficulty is then added to the within form item calibrations to place every administration of every item onto one common bank scale.
Calibrating Forms on the Bank
To estimate the shift in difficulty between two forms, k and j, a weighted average of difficulty differences is calculated for items linking them
Vi = sum([dij - dik]/wijk) / sum[1/wijk] i=1,n (4)
where dik and dij are the estimated difficulties of linking item i in forms k and j, n is the number of items in this link, and 1/Wikj = 1/ [seik² + seij²] is an information weight based on the calibration standard errors, seik and seij. The standard error of tkj is
sekj² = 1/sum(1/wikj) i=1,n (5)
Shift tkj estimates the difference in origins of forms k and j. A shift is calculated for every pair of forms linked by common items. The difficulty Tk of form k is the average shift for form k over all forms.
Tk = sum(tkj)/M j=1,M (6)
where M is the number of forms and tkk = 0. The standard error of Tk is
sek² = sum(sekj²)/M² j=1,M (7)
Equations 4 through 7 assume every form is linked to every other form. When links are missing between some forms, as is usually the case, empty cells can be started at
tkj = 0, (8)
and improved by calculating form difficulties with Equation 6 and adjusting empty cells to
tkj = Tk - Tj (9)
until the Tk stabilize. This process works as long as every form can be reached from every other form by some chain of links.
The bank origin is at the center of the forms so that form difficulty Tk is the difference between the center of form k and the center of the bank.
Item-Within-Link Fit Analysis
SHIFT fit analysis focuses on the existing links between forms. First, SHIFT verifies the extent to which linking items perform adequately within their forms. This is done by combining the item-within-form fit statistics of Equation 3 into a within- form fit statistic for the link.
Within form fit = sum(Vik + Vij)/2n i=1,n (10)
where Vik is the fit of item i in form k, Vij is the fit of item i in form j, and n is the number of items in the link. This statistic approximates one with variance about 1/n(N-1) when link items fit within forms.
Item-Between-Link Fit Analysis
Second, SHIFT checks the extent to which link items agree on the relative difficulties of their two forms. This fit statistic is a ratio of observed to modeled variance.
Between link fit = Sum(d'ik - d'ij)² / Sum(wikj) i=1,n (11)
where the within form item difficulties, dik, have been translated to their bank values d'ik by
d'ik = djk + Tk ( 12)
and Wikj = [seik² + seij²]. Values substantially greater than one, given expected variance 2/(n-1), signify that some items operate differently in the two forms. A plot of d'ik versus d'ij over i facilitates the evaluation of link status and the identification of aberrant items (Wright & Masters, 1982, pp. 114-117; Wright & Stone, 1979, pp. 92-95).
Link-Within-Bank Fit Analysis
Third, SHIFT checks the extent of agreement among links with respect to form difficulties. Each entry in the matrix of observed shifts between forms should be close to the difference in bank difficulties of its forms. To evaluate whether a link fits the bank a link residual is calculated
ykj = tkj - [Tk - Tj] (13)
where tkj is the observed shift between forms k and j, and Tk and Tj are their bank difficulties. These link residuals can be standardized to mean zero and variance one by dividing them by the standard errors, sekj, of their tkj of Equation 5 and multiplying by [M/(M - 2)]^0.5 where M is the number of forms in the linking network.
Form-Within-Bank Fit Analysis
Finally, SHIFT checks the fit of each form to the bank as a whole by calculating
Vk = sum[ykj/sekj]² [M/(M-2)] /(L-1) j=1,L (14)
where L is the number of tkj observed for form k. The criterion value of Vk is one with variance about 2/(L-1).
The fit of a link or form into the bank is related to how well linking items fit within their own forms. When the number of students taking a form is large, the item fit statistic variances can become unrealistically small and should be used with caution. Careful investigation of doubtful items is always instructive and invariably leads to insight into the nature of the variable. The misfit of links within the bank is usually associated with particular forms. This can occur when a form is inadvertently administered to a sample of students for whom it is inappropriate. The best items for estimating form difficulties are those that satisfy the various fit analyses.
Showing the Resulting Bank
Program ITEMLIST is used to list each item in the bank by sequence number, legitimate alternatives, correct response, item name, bank difficulty, between difficulty root mean square, and within form fit mean square.
Bank difficulty is the average of the item's difficulties in the forms in which it was calibrated, adjusted for these forms' difficulties. The between difficulty root mean square is the square root of the average squared difference between an item's bank equated difficulties in each form and its bank difficulty. It is useful to tag items with between difficulty root mean squares greater than 0.5 logits for examination because they are frequently found to have been miskeyed or misprinted in one of the forms in which they appear.
The within form item fit mean square of Equation 3 is standardized to mean zero and variance one and the average square of these standardized within form fits is used to summarize item performances within forms. Its sign is taken from the sign of the standardized fit with the largest absolute value to distinguish between misfit caused by unexpected disorder, indicated by large positive standardized fits, and misfit caused by unexpected within form inter-item dependence, indicated by large negative standardized fits. It is useful to tag items producing values greater than 2 or less than -2 for further examination.
Program ITEMMAP is used to display the variable graphically by plotting the items, according to their bank difficulties, along the line of the variable which they define. This enables teachers to examine the relationship between the content of the items and their bank difficulties in order to review the extent to which the item order defines a curriculum strand that agrees with their expectations and so has construct validity. It also provides a framework for writing new items to fill gaps that appear in the definition of the curriculum strand and for choosing items for new tests.
Program FORMLIST is used to list each form by form number, name, number of items, and bank difficulty. Each item is listed by form position, item name, key, within form difficulty and standard error, total within form standardized fit, and bank difficulty. This facilitates the review of each form as a whole and the identification of form specific anomalies.
Program KIDLIST is used to list each student by identification, ability measure, error, and fit statistic. KIDLIST indicates students who misfit by displaying their response string and its residuals from expectation, so that teacher and student can see the specific sources of misfit.
Program KIDMAP is used to provide a graphical representation of each student's performance. KIDMAP makes an item response map for each student which shows where the student and the items taken stand on the curriculum strand, which items were answered correctly, the probability of each response, and the student's percent mastery at each item. This provides teacher and student with a picture of the student's performance which combines specification of criteria mastery with the identification of unexpected strengths and weaknesses.
HOW TO CONTROL ITEM QUALITY
Once items have been banked, the identification and study of misfitting items follows. The irregularities most often identified are mechanical and clerical such as miskeying, misprinting, misscoring, more than one right answer, and no right answer. Table 2 shows the statistics of some misfitting items from a mathematics and a reading bank.
The discrimination index in Table 2 is one plus the regression of the student-by-item logit residual (x - p)/[p(1 - p)] on the person ability b over the sample of students. It indicates the degree to which the item differentiates between abilities. Discriminations less than one imply noise in item use, outbreaks of guessing or carelessness, or the presence of secondary variables correlated negatively with the intended variable. Discriminations greater than one imply items unreached by or not yet taught to low scoring students, response formats or item contents that introduce inter-item dependencies, or the presence of secondary variables correlated positively with the intended variable.
The between fit statistic in Table 2 is a between score group mean square calculated from Equations I and 2 accumulated over score groups (Wright & Panchapakesan, 1969, pp.44-46) and standardized to mean zero and variance one (Wright & Masters, 1982, p. 101). The total fit statistic is the mean square of Equation 3 similarly standardized.
Miskeying usually produces a characteristic misfit pattern. The item appears more difficult than anticipated, the between fit is large, the discrimination low. Item No. 277 in Table 2 illustrates this. Its calibration implies that it is very difficult, but it requires an easy task, "What does the symbol '-' mean?" The other items that deal with the recognition of addition and subtraction symbols are easy. Investigation revealed that division rather than subtraction was the keyed right answer. Correcting the key and rescoring rescued item No. 277 from its misfit status and gave it a new difficulty which placed it among other items of its type.
Misfit caused by student behavior, such as guessing and carelessness, is not diagnosed well by item fit statistics because item statistics lump together students behaving differently. Disturbances that are the consequences of individual student behavior are best detected and best dealt with through the fit analysis of individual students (Smith, 1982, 1984; Wright & Stone, 1979, chaps. 4 & 7). But item statistics can call attention to items that tend to provoke irregular behavior.
| TABLE 2 Some Misfitting Items from a Mathematics and a Reading Bank | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Subj | Item Number | Form Number | Bank Diff | S.E. | Point Biser | Discr Index | Betwn Fit | Total Fit | Diagnosis |
| Math | 277 | 310 324 |
4.41 4.04 |
0.52 0.39 |
-0.06 -0.11 |
-0.50 -0.19 |
9.50 10.59 |
0.38 1.09 |
Miskey/ Misprint |
| Math | 256 | 314 321 |
2.77 3.02 |
0.30 0.34 |
0.11 0.02 |
0.38 0.05 |
6.61 10.23 |
0.82 0.77 |
Guessing |
| Read | 339 | 112 | 2.07 | 0.28 | 0.10 | 0.11 | 6.81 | 1.85 | Guessing |
| Read | 23 | 115 128 |
2.28 3.45 |
0.34 0.33 |
-0.02 0.14 |
0.06 0.44 |
6.56 5.01 |
-0.35 1.62 |
Guessing |
| Math | 258 | 304 | -2.83 | 0.72 | -0.03 | 0.24 | 6.48 | -0.05 | Careless |
| Math | 9 | 319 | -1.49 | 0.37 | -0.06 | -0.01 | 6.23 | 0.82 | Careless |
| Read | 92 | 132 | -0.85 | 0.35 | 0.32 | 0.84 | 5.15 | 0.05 | Careless |
Guessing is only a problem when some low-ability students are provoked to guess on items that are too difficult for them. The characteristic item statistic pattern is high difficulty, high between fit, and low discrimination. Item Nos. 256, 339, and 23 in Table 2 illustrate this.
Item No. 256 shows a map and asks: "Bill followed the path and went from home to the mountains for a picnic. How far was his round trip if he went the shortest way possible?" Except for the requirement that students know that "round trip" means the same as "from X to Y and back" this item is similar to the other items in its skill. Perhaps uncertainty concerning the meaning of "round trip" provoked some low-scoring students to guess on this item.
Item No. 339 appeared to be one of the most difficult items in the reading bank. Item No. 23 appeared to be the hardest item in its forms. The item characteristic curves for these items were flat implying that low-scoring students answered them correctly about as often as high-scoring students. These items were found to share an ambiguous correct alternative. Item No. 339 reads: "The word that has the same sound as the 'e' in 'problem' is:" with alternatives: "ago," "eat," "out," "ink." Item No. 23 reads: "The word that has the same sound as the 'ou' in 'famous' is:" with alternatives: "own," "you," "ago," "odd." "Ago," the correct answer to both, is the only alternative in this skill containing two vowel sounds. Only three or four students in each ability group responded "ago." It seems reasonable to infer that many of these few successes were guesses. Which students actually guessed, however, can only be determined by examining each student's individual performance pattern and evaluating the extent of improbable correct answers to these (and other) items.
Carelessness occurs when some high-ability students fail easy items. The pattern in item statistics is low difficulty, high between fit, and low discrimination. Item Nos. 258, 9, and 92 in Table 2 illustrate this.
Item No. 92 reads: "In this story, 'don't' means the same as:" with alternatives: "do no," "do not," "did not," "does not." Misfit was traced to a high-scoring group in which more students than expected chose the incorrect alternative "do no." As this error is particularly glaring, and this item was easy for low- scoring students, carelessness is implied. Perhaps the distractor "do no" was misread as "do not" by some able students in a hurry. The identification of which particular students were careless, however, requires the examination of each student's individual performance pattern and an evaluation of the extent of improbable wrong answers to these (and other) items.
When the disturbance in a misfitting item is not mechanical or clerical, the cause can often be traced to special knowledge such as knowing that multiplication by zero is different than multiplication by other numbers. Interactions with exposure can also affect the shape of the response curve. Dependence on a skill that only high-ability students have been taught can make an item unfairly easier for these high-ability students. This will cause the item to have a discrimination index larger than one and a fit statistic that is too low. On the other hand, dependence on a skill that is negatively related to instruction, so that low-ability students tend to possess more of it, can make an item unfairly easier for low-ability students and, hence, give it a discrimination index smaller than one and a fit statistic that is too high. Either way, the interaction disqualifies the item for use with students who are unequal in their exposure to the special skill. If discrimination is too low, the item is unfair to more able students. If discrimination is too high, the item is unfair to less able students.
BENJAMIN D. WRIGHT AND SUSAN R. BELL
MESA Research Memorandum Number 43
MESA PSYCHOMETRIC LABORATORY
REFERENCES
BROGDEN, H. E. (1977). The Rasch model, the law of comparative judgement and additive conjoint measurement. Psychometrika, 42, 631-634.
CHOPPIN, B. (1968). An item bank using sample-free calibration. Nature, 219, 870-872.
CHOPPIN, B. (1976). Recent developments in item banking. In Advances in psychological and educational measurement. New York: Wiley.
CHOPPIN, B. (1978). Item banking and the monitoring of achievement (Research in Progress Series No. 1). Slough, England: National Foundation for Educational Research.
CHOPPIN, B. (1981). Educational measurement and the item bank model. In C. Lacey & D. Lawton (Eds.), Issues in evaluation and accountability. London.
CONNOLLY, A. J., NACHTMAN, W., & PRITCHETT, E. M. (1971). KeyMath: Diagnostic arithmetic test. Circle Pines, MN: American Guidance Service.
CORNISH, G., & WINES, R. (1977). Mathematics profile series. Hawthorn, Victoria: Australian Council for Educational Research.
ELLIOTT, C. D. (1983). British ability scales, manuals 1- 4. Windsor, Berks: NFER-Nelson.
ENGLEHARD, G., & OSBERG, D. (1983). Constructing a test network with a Rasch measurement model. Applied Psychological Measurement, 7, 283-294.
IZARD, J., FARISH, S., WILSON, M., WARD, G., & VAN DER WERF, A. (1983). RAPT in subtraction: Manual for administration and interpretation. Melbourne: Australian Council for Educational Research.
KOSLIN, B., KOSLIN, S., ZENO, S., & WAINER, H. (1977). The validity and reliability of the degrees of reading power test. Elmsford, NY: Touchstone Applied Science Associates.
LUDLOW, L. H. (1983). The analysis of Rasch model residuals. Unpublished doctoral dissertation, University of Chicago.
MEAD, R. J. (1975). Analysis of fit to the Rasch model. Unpublished doctoral dissertation, University of Chicago.
RASCH, G. (1980). Probabilistic models for some intelligence and attainment tests. Chicago: University of Chicago Press. (Original work published 1960)
RENTZ, R., & BASHAW, L. (1977). The national reference scale for reading: An application of the Rasch model. Journal of Educational Measurement, 14, 161-179.
SMITH, R. M. (1982). Detecting measurement disturbances with the Rasch model. Unpublished doctoral dissertation, University of Chicago.
SMITH, R. M. (1984). Validation of individual response patterns. In International Encyclopedia of Education. Oxford: Pergamon Press.
STONE, M. H., & WRIGHT, B. D. (1981). Knox's cube test. Chicago: Stoelting.
WOODCOCK, R. W. (1973). Woodcock Reading Mastery Test. Circle Pines, MN: American Guidance Service.
WRIGHT, B. D. (1968). Sample-free test calibration and person measurement. In Proceedings of the 1967 Invitational Conference on Testing Problems. Princeton, NJ: Educational Testing Service.
WRIGHT, B. D. (1977). Solving measurement problems with the Rasch model. Journal of Educational Measurement, 14, 97- 116.
WRIGHT, B. D. (1983). Fundamental measurement in social science and education (Research Memorandum No. 33). Chicago: University of Chicago, MESA Psychometric Laboratory.
WRIGHT, B. D., & MASTERS, G. N. (1982). Rating scale analysis. Chicago: MESA Press.
WRIGHT, B. D., & PANCHAPAKESAN, N. (1969). A procedure for sample-free item analysis. Educational Psychological Measurement, 29(1), 23-48.
WRIGHT, B. D., & STONE, M. H. (1979). Best test design. Chicago: MESA Press.
AUTHORS
BENJAMIN D. WRIGHT, Professor of Education and Behavioral Science, Chair, MESA Special Field, Director, MESA Psychometric Laboratory, University of Chicago, 5835 Kimbark Avenue, Chicago, IL 60637. Degrees: BS, Cornell University; PhD, University of Chicago. Specializations: Measurement, psychoanalytic psychology.
SUSAN R. BELL, Research Associate, MESA Psychometric Laboratory, University of Chicago, 5835 Kimbark Avenue, Chicago, IL 60637.
This appeared in
Journal of Educational Measurement
21 (4) pp. 331-345, Winter 1984
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo43.htm