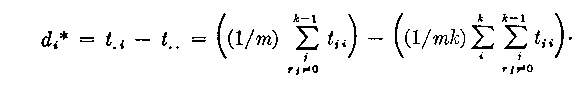 (18)
(18)Our purpose is to describe in detail a convenient procedure for performing a new kind of item analysis. This new item analysis is different in a vital way from that described in textbooks like Gulliksen's Theory of Mental Tests and used in computing programs like TSSA2. The difference is that (a) test calibrations are independent of the sample of persons used to estimate item parameters, and (b) person measurements, the transformation of test scores into estimates of person ability, are independent of the selection of items used to obtain test scores.
The procedure for sample-free item analysis is based on a very simple model (Rasch, 1960, 1966a, 1966b) for what happens when any person encounters any item. The model says that the outcome of such an encounter is governed by the product of the ability of the person and the easiness of the item and nothing more! The more able the person, the better his chances for success with any item. The more easy the item, the more likely any person is to solve it.
This means that variation in additional item characteristics, like guessing and discrimination, must be dealt with during the construction and selection of items for the final sample-free pool. The aim is to create a pool of items with similar discrimination and minimal guessing. Since the method for measuring person ability is quite robust with respect to departures from the assumption that the only characteristic on which items differ is easiness, this aim is not difficult to satisfy. The procedure to be described includes a statistical test for item fit which facilitates the identification of "bad" items which do not conform to the assumptions of the model. [BDW would later say "specifications of the model."]
The use of this simple model for mental measurement makes it possible to take into account whatever abilities persons in the calibration sample happen to have and to free the calibration of test items from the particulars of these abilities. As a result no assumptions need be made about the distribution of ability in the target population or in the calibration sample.
In its mathematical form this model for sample-free item analysis says that the observed response ani of person n to item i is governed by a binomial probability function of person ability Zn and item easiness Ei . The probability of a right response is:
Pr(ani = 1) = Zn Ei /(1 + Zn Ei ) (1)
and the probability of a wrong response is:
Pr(ani = 0) = 1 - Pr(ani = 1) = 1/(1 + Zn Ei ). (1')
Taking advantage of the convention that ani = 1 means right and ani = 0 means wrong we can combine (1) and (1') to give:
Pr(ani ) = (Zn Ei )ani/(1 + Zn Ei ) (2)
It is also convenient to express (2) in an alternative form in which we write the model parameters Zn and Ei in a log form as follows:
Pr(ani ) = exp (ani (bn + di ))/(1 + exp(bn + di )) (3)
where bn = log Zn and di = log Ei .
An important consequence of this model is that the number of correct responses to a given set of items is a sufficient statistic for estimating person ability. This score is the only information needed from the data to make the ability estimate. Therefore, we need only estimate an ability for each possible score. Any person who gets a certain score will be estimated to have the ability associated with that score. All persons who get the same score will be estimated to have the same ability.
This encourages us to rewrite (3) in terms of score groups.
Pr(ani ) = exp (ani (bj + di ))/(1 + exp(bj + di )) (4)
where j is the score obtained by person n and all persons with a score j are estimated to have the same probability governing their responses to item i.
There are two stages in the measurement of person ability. The first stage, item calibration, consists in estimating the item parameters di and their standard errors. This is done by analyzing the responses of a sample of N persons to a set of k items. It is during this stage that items are discarded which do not satisfy the criteria considered important from the point of view of the model. In typical item analysis desirable characteristics of a test are high reliability and validity, therefore items with low indices of reliability or validity are dropped. For this sample-free model the essential criterion is the compatibility of the items with the model.
The failure of an item to fit the model can be traced to two main sources. One is that the model is too simple. It takes account of only one item characteristic - item easiness. Other item parameters like item discrimination and guessing are neglected. As a matter of fact, parameters for discrimination and guessing can easily be included in a more general model. Unfortunately their inclusion makes the application of the model to actual measurement very complicated, if not impossible. The sample-free model assumes that all items have the same discrimination, and that the effect of guessing is negligible. Our experience with the analysis of real data suggests that the model is quite robust with respect to departures from these assumptions.
The other source of lack of fit of an item lies in the content of the item. The model assumes that all the items used are measuring the same trait. Items in a "test" may not fit together if the "test" is composed of items which measure different abilities. This includes the situation in which the item is so badly constructed or so mis-scored that what it measures is irrelevant to the rest of the "test."
If a given set of items fit the model this is the evidence that they refer to a unidimensional ability, that they form a conformable set. Fit to the model also implies that item discriminations are uniform and substantial, that there are no errors in item scoring and that guessing has had a negligible effect. Thus the criterion of fit to the model enables us to identify and delete "bad" items. Item calibration is concluded by reanalyzing the retained items to obtain the final estimates of their easinesses.
In the second stage, person measurement, some or all of the calibrated items are used to obtain a test score. An estimate of person ability and the standard error of this estimate are made from the score and from the easinesses of the items used. The flexibility of being able to use some or all of a set of items in a "test" is an important advantage of this method of item analysis. Meaningful comparisons of ability can be made even when the particular items used to make the different measurements are not the same. The number of items selected for any measurement can be determined by the testing time available and the accuracy required.
In this procedure the "reliability" of a test, a concept which depends upon the ability distribution of the sample, is replaced by the precision of measurement. The standard error of the ability estimate is a measure of the precision attained. This standard error depends primarily upon the number of items used. The range of item easiness with respect to the ability level being measured, also affects the standard error of the ability estimate. But in practice this effect is minor compared to the effect of test length. It is possible to reach any desired level of precision by varying the number of items used in the measurement, just providing that the range of item easiness is reasonably appropriate to the abilities being measured.
We shall describe two methods for the estimation of item and person parameters and their standard errors. Both methods are such that ability estimates are obtained at the same time as item estimates. The equations used for person measurement, given calibrated items, are similar to those used during item calibration. The difference being that during person measurement the items are assumed calibrated, and so item easinesses are no longer estimated but kept fixed. However, one is not usually interested in ability measurement at the stage of item calibration. Usually a pool of items are calibrated first and then later used selectively for measurement.
The first method of estimation uses unweighted least squares and will be referred to as LOG. The second method uses maximum likelihood and will be referred to as MAX [also known as UCON and JMLE]. In general MAX is preferable to LOG. MAX gives better estimates of the model parameters, and the standard errors of estimate are better approximated. However, when the calibration sample is large, and the ability range of the sample is wider than the easiness range of the item parameters, then the item estimates obtained by LOG are equivalent to the estimates obtained by MAX.
In general we recommend that MAX be used whenever possible. Our reason for describing LOG is that it is conceptually and computationally simple. If a small computer is unavailable, LOG can be used to obtain rough parameter estimates and their standard errors.
Despite the simplicity of LOG we would like to emphasize that MAX is not much more complicated. The characteristic which makes MAX more difficult to use is its system of implicit equations which must be solved by an iterative procedure. This iterative procedure is easy to perform on a small computer but tedious on a desk calculator.
Methods
A. LOG Method:
1. Description.
The log method of estimation is based on using the observed proportion of successes aji /rj within a particular score group j as an estimate of the probability pji of obtaining a correct response, for any person in score group j, to an item of easiness Ei = exp di .
pji ~= aji /ri
pji = exp (bj + di )/(1 + exp(bj + di )) (5)
where bi is the ability associated with
score group j
ri is the number of persons in score group
j
aji is the number of persons in score group
j who get item i correct.
and (ri - aji )/ri ~= 1/(1 + exp (bj + di ))
so aji /(ri - aji ) ~= exp (bj + di )
and tji = log (aji /(ri - aji )) ~= bj + di , (6)
so tji = bi * + di * (7)
where di * = estimate of di
and bj * = estimate of bj .
This leads to the estimation equations
di * - d. * = t.i - t.. (8)
where d. * = (1/k) sum i=i to k (di *)
t.i = (1/(k - 1)) sum j=1 to k-1 tji
t.. = (1/k) sum i=1 to k t.i
Since there is an indeterminacy in the scale of easiness we can determine the scale so that d. * = 0 to give:
log Ei * = di * = t.i - t.. (9)
as the basic equation for estimating item easiness.
We also obtain an estimation equation for ability:
log Zj * = bj * = tj. - t.. (10)
Equations (9) and (10) are the basic estimation equations for the log method.
To calculate standard errors of the estimates bj * and di * we need expressions for the variance of tji . This is obtained from the variance of aji . The number of successes aji in the score group j has a binomial distribution, and hence the variance of aji , will be given by:
V(aji ) = ri pji (1 - pji )
where pji is the probability of obtaining a success. The variance of tji can be approximated from:
V(tji ) ~= (dtji /daji )2 V(aji )
~= 1/ri pji (1- pji )
or V*(tji ) = 1/ri pji *(1-pji *) (11)
where pji * = exp (bj * + di *)/(1 + exp (bj * + di *))
and (dtji /daji ) is the partial derivative of tji with respect to aji and equals 1/ri pji *(1-pji *)
From (9) we get for the variance of di *:
V(di *) = V(t.i - t.. ).
We know that the tji 's are independent with respect to variation in j, that is for given i, tji and tli are independent, because they come from different groups of persons. However, there is a relationship between tji and tjl , for any score group j because of the constraint sum i=1 to k aji - jri . In fact, the actual covariances between tji and tjl are very small. For simplicity we will assume that the tji 's are independent of each other in both directions. Then for the variance of di * we get:
V(di *) ~= (1 - 1/k)V(t.i ) < V(t.i )
so ~= V(t.i )
V*(di *) = (1/(k - 1)2 ) sum from i=1 to k-1 V(tji ). (12)
This approximation is conservative. The exact variances of estimates are smaller than those given by (12). The standard error of the ability estimate is approximated by:
V*(bi *) = (1/k2 ) sum from i=1 to k V(tji ). (13)
Procedure
A. Data Handling
The observations consist of the responses of N individuals to each of k items which compose the test. The response to an item is coded 1 or 0, 1 if the response is correct and 0 otherwise. (The procedure is restricted to dichotomous items, i.e., to items that can be coded right or wrong.)
A k-dimensional response vector I of 1's and 0's can represent the response of an individual to the test. Hence, the data could be conceived of as an N x k matrix containing the responses of all the N persons to the k items. However, for estimation that matrix contains superfluous information because the ability estimate of an individual is entirely dependent on his score - the exact pattern of responses is immaterial. We do not need to know the response of an individual to a particular item, but only his total score to classify him according to estimated ability.
The distribution of estimated ability for the whole sample can be summarized in a score vector R of dimension k-1. The element rj of the vector R is set equal to the number of persons with a score of j.
Scores of 0 and k are excluded because they do not contribute to the item calibration. They provide no differential information about the items. For these people all the items appear either equally hard or equally easy. In fact we cannot obtain point estimates of ability for such people. Items which everyone gets right or everyone gets wrong are also excluded. At the calibration stage we cannot obtain point estimates for them from the sample, and at the measurement stage at least among the calibrating sample they do not provide differential information about the ability of the individuals being measured.
Thus the original N x k data matrix can be collapsed into a (k - 1) x k matrix A, such that an element aji represents the number of persons with a score of j who get item i correct. This A matrix contains all the information bearing on test calibration.
The first step in the procedure then consists in computing A and R. The total number of persons N' (excluding those that get zero and maximum scores) can be counted at the same time. The most convenient way of setting up the matrix A and vector R is to read in one case (vector I) at a time. The score j is calculated by summing over all the responses.
j = sum i=1 to k (Ii ) (14)
or jn = sum i=1 to k ani .
If j = 0 or k the case is disregarded and the next case is read in. When j is in the permissible range the appropriate accumulation is made to R and A. This is demonstrated below in terms of a FORTRAN program segment which can be used as a subroutine acting on each case:
[Obsolete source code omitted]
I = Response vector I
IA = Matrix A in fixed point
K = Number of items k in test
RN = N' number of persons with scores not 0 or K
R = Vector R of score group sizes.
It is assumed that IA, R and RN are zeroed before any cases are accumulated into them.
If any rj is zero we disregard the score group j. An empty score group does not contribute any information to the item estimation or to the test for the item fit. Also in the case of the log method we cannot obtain ability estimates directly for empty score groups. Therefore, the number of useful score groups are score groups which have one or more persons in them. We compute m, the number of such useful score groups by scanning the vector R,
m = sum i=1 to k-1 xi (15)
where xi =1 if ri >0
xi = 0 if ri = 0.
The information from the data contained in R, A, N' and m is enough to enable us to estimate the model parameters and their standard errors.
b. Estimation
To get estimates by the log method we transform the data in A to a matrix T where the element tji is given by
tji = log (aji /(ri - aji )). (16)
We run into problems when aji = 0 or when aji = ri , because at these values tji is infinite. To avoid this difficulty we modify T such that:
tji = log ((aji +w)/((ri - aji +w)). (17)
where w = ri /N'.
The advantage of this adjustment is that now when aji = 0 or aji = ri then tji = ±log (1 + N'). These limits for extreme values of tji seem reasonable, because for N' persons log(1 + N') is an outside limit on the magnitude that any cell in T can take. Thus the matrix T is set up using the expression (17) for each element of the matrix.
The estimates di * are obtained from T using (9)
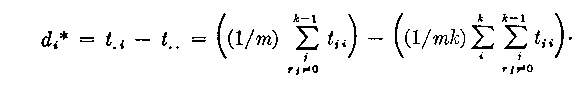 (18)
(18)
In principle this is as far as we need proceed to obtain item estimates by the log method, but the di *'s obtained above contain the extreme values for the empty and full cells in A, i.e., when aji = 0 or aji = ri . We can improve the estimates by substituting values for the unknown tji 's according to the model. To do this we also need the ability estimates, which are obtained from T by (10)
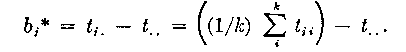 (19)
(19)
From the model the estimated value we get for the cell tji is:
tji * = di * + bj * + t.. (20)
therefore for the extreme cells we substitute this value in place of ±log(1 + N').
With these new values for the unknown cells in T we again compute di * and bj * according to (18) and (19). The results will differ from the previous values depending upon the number of empty and full cells in the matrix A.
The program steps in FORTRAN required for obtaining the estimates di *, bj * and the matrix T are shown below.
[obsolete source code omitted]
B is the vector of ability estimates
D is the vector of item estimates.
Methods
B. MAX Method:
1 Description.
Maximum likelihood is a widely used method for estimating model parameters. The assumption involved in obtaining parameter estimates is that the observed data is the most likely occurrence. Parameters are estimated so that they maximize the probability (likelihood) of obtaining the sample of observations.
The equations obtained when the condition of a maximum likelihood is satisfied for the sample free model (3) in the introduction are:
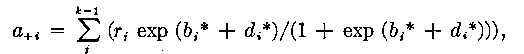
i=1,2...k (21)
![]()
i=1,2...k-1 (22)
where a+i = number of persons who get item i correct (item score)
j = the score, an ability estimate is obtained for each score
ri = number of persons in score group j,
and the log likelihood is
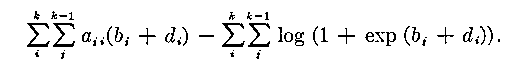
The method consists in computing di * and bj * from the implicit equations (21) and (22). It should be noted that each of the equations (21) involves only one item estimate, even though it does depend on all (k - 1) ability estimates bj *. Similarly, each equation in (22) involves only one ability estimate and of all the item estimates di *. We handle these equations as two independent sets, and solve them accordingly.
When the item estimates are assumed known, (22) is the set of equations used for person measurement. From (22) we can obtain a scoring table, a table which will show the estimated ability corresponding to every score, for a given set of items. This scoring table involves only the item estimates. Therefore, a scoring table can be provided for any specific test, and the ability of an individual can be estimated by looking up his score in the scoring table. Once the scoring table is obtained no further computations are necessary. Thus computations are in general only necessary at the item calibration stage. They become necessary at the measurement stage only if one does not want to use a set of items for which a scoring table has been provided.
The approximation of a standard error for item estimates can be approached in two ways. In equation (21) we can assume that the variance of the item estimate is due primarily to the uncertainty in the item score a+i . To a first approximation this gives:
![]()
which from (21) leads to:
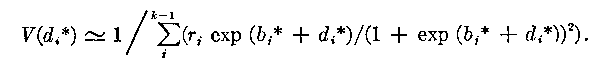 (23)
(23)
An alternative is to approximate the standard error f m the asymptotic value of the variance of a maximum likelihood estimate. But this leads to the same equation (23).
To obtain estimates for the item parameters, we have to solve the two sets of equations (21) and (22). Since these equations are implicit in di * and bj *, we cannot solve them directly. In our analysis we use the Newton-Raphson procedure to solve for the unknown parameter estimates. This procedure is an iterative one. We start with an initial estimate x0 , and using the Newton-Raphson equation obtain an improved estimate x1 . Now using the new value x1 as the starting estimate, we repeat the procedure until the estimates do not change appreciably. If f(x) = 0 is the implicit equation to be solved for x, the value of x at the (n+1)th iteration is given by
xn+1 = xn - (f(xn )/f'(xn )) (24)
where xn = value of x at the nth iteration
f'(x) = df(x)/dx, the differential of f(x) with respect to x and f(x)/f'(x) is evaluated at x = xn .
Equation (24) is suitable for equations which are functions of only one unknown. This is adequate for our purposes because we can solve (21) and (22) as two independent sets of equations, in which each of the k equations in (21) and each of the (k - 1) equations in (22) are locally functions of only one unknown.
To facilitate a description of the procedure we write equations (21) and (22) in a form analogous to equation (24).
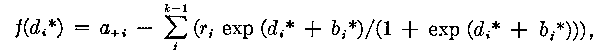
i = 1, 2 ... k
![]() (25)
(25)
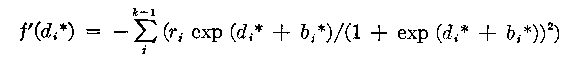 (26)
(26)
j = 1, 2 ... k-1
Also if
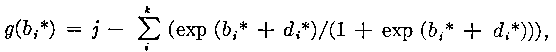
j = 1, 2 ... k-1
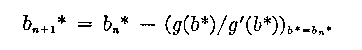 (27)
(27)
![]() (28)
(28)
Since the method is iterative, we need some basis for termination. We employ two different criteria for judging whether convergence has been reached. An obvious consideration is to look at the average squared difference SD between the values of estimates obtained from two consecutive iterations. If SD is less than some criterion value SC, we stop the procedure, because insufficient improvement is obtained in the estimates by continuing the procedure further. An alternate criterion is to monitor the value of the likelihood function. This can be accomplished by computing the likelihood at each iteration and observing the rate of increase. If things are as they should be, the likelihood will increase rapidly at first, and then become approximately constant. The procedure can be stopped when the increase in the likelihood is less than some specified value CM.
Procedure
The first part of the procedure for MAX is the same as that described for LOG. The data is edited in exactly the same way, and the LOG procedure followed until initial item estimates are obtained. These item estimates are then used as the initial values for the iterative procedure described in MAX. The initial values for the ability estimates are taken to be zero.
Using the LOG item estimates and zero ability estimates as starting values, the iterative procedure, described by the Newton-Raphson equations (25) and (27), is continued until stable estimates are obtained both for the item and the ability estimates.
This is accomplished by solving (25) for the item estimates assuming that the abilities are zero. The obtained item estimates are substituted in (27) and these equations are solved for improved ability estimates. The improved ability estimates are then substituted in (25) and improved item estimates obtained. This procedure of alternately solving (25) and (27) using improved estimates at each stage is continued till the process converges.
Two criteria for convergence were described in the previous section. We use both criteria. First we examine the average squared deviation SD and then test the change in the likelihood ELD. If either SD or ELD is less than the specified criterion value we stop the procedure. The criterion values we use are 10-5 for SD and 10-2 for ELD. We find that these cut-off values ensure sufficient convergence. When the procedure is continued further no appreciable change is observed in the estimates. The FORTRAN programming steps required for implementing the successive solutions for (25) and (27) are shown below:
[obsolete source code omitted]
The log likelihood EL is initialized at a negative value since it is expected to increase. This is necessary to do in order to compute the change in the likelihood for the first iteration. The vector B, ability estimates, are initially set to zero, and the vector D, item estimates, are those obtained from the LOG method. From our experience we find that the maximum number of times we might expect to go through this procedure is less than 20, therefore we set the maximum index of the loop at 20. SC and CM are the criterion values discussed above, e.g. SC = 10-5 and CM = 10-2 and
K = number of items
NGK = K - 1, the number of score groups
R = vector of score group sizes
IA = data matrix in fixed point mode.
AP is the vector of item scores which can be computed from the data matrix as follows:
APi = sum i=1 to k-1 aji .
MAXLIK and LIKE are subroutines. MAXLIK performs the iterations for the individual sets of equations, i.e. for (25) and (27). LIKE computes the likelihood. The steps required for these subroutines are indicated below.
[obsolete source code omitted]
It should be noted that, as in the LOG method, here also the item estimates are constrained so that they add to zero, i.e. sum from i=1 to k di * = 0. The iterations for the Newton-Raphson method are performed in subroutine NEWT. It is a general subroutine and is applicable to any equation of the form:
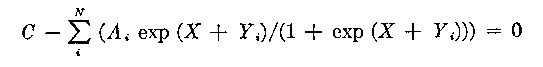
where X = the unknown
C, and vectors A and Y are given constants.
The steps required for the programming are shown below:
[obsolete source code omitted]
Finally Subroutine LIKE is given below:
[obsolete source code omitted]
Once the item and ability estimates have been obtained, by the procedure described above, the standard error of item estimates is easily computed from equation (23). The vector SI of standard errors of the item estimates depends mainly upon the number of persons in the sample, i.e., the vector R of score group sizes. The larger the elements of this vector R, the smaller will be the standard errors. The program segment for computing SI is shown below:
[obsolete source code omitted]
Methods
C. Person Measurement
1. Ability Estimation:
This part of the procedure is especially important for test users. Ordinarily test users are not concerned with calibrating items. Given a pool of calibrated items, however, they want to estimate abilities for persons to whom sets of items have been administered.
As mentioned earlier, if a scoring table is provided with the items and all the items used to compute the scoring table are used in the test, there is no need to compute new ability estimates. They can be obtained immediately by referring to the scoring table. If only some of the items are used, however, one needs to compute the abilities and their standard errors for scores on this selection of items. That procedure is given in this section.
The equations to be solved have been discussed previously (22). The only way to solve these implicit equations (22) is by means of an iterative method. The Newton-Raphson procedure gives the relationship between two successive values of the estimates in terms of the functional form of the equation to be solved. This procedure was discussed previously (27), but we will restate the equations for the convenience of those interested in ability estimation only.
 j=1,2,...,k-
1
j=1,2,...,k-
1
j = the score, an estimated ability bj * is associated with each score
di = the item estimates, assumed known from the calibration of the item pool
k = number of items used for the test.
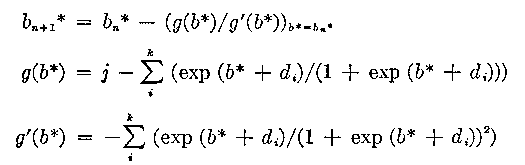
bn * = value of the estimate at the nth iteration
bn+1 * = value of the estimate at the (n+1)th iteration
g(b*)/g'(b*) is evaluated at b* = bn *.
Since we are solving the equations by means of an iterative method, we need some criterion for terminating the procedure. We stop the iterations when SD, the square of the relative change in the estimate, is less than some specified value SC. We find that no appreciable change is observed in the estimates if the procedure is carried on beyond the point when SD becomes less than 10-6. Therefore, we set SC = 10-5.
The FORTRAN program segment for this procedure is given below:
[obsolete source code omitted]
Thus we obtain an ability estimate for each of the k-1 scores 1, 2 ... k-1. One advantage of using this metric for the abilities instead of the observed score is that the scale of this metric is an interval scale, whereas, in general the raw score scale is not. Another important consideration is that abilities in this metric, obtained from different sets of calibrated items, are comparable. In the case of the raw score there is no rigorous method of putting the score on a common scale.
2. Standard Error of Ability Estimate:
The accuracy [precision] of any ability measurement is an important consideration. Not only do we want to be able to measure the ability of a person, but we would also like to know how well we have been able to make the measurement. The major contribution to the error variance of the ability estimate comes from the variance in scores produced by a given individual. As we shall later see, this part of the error variance depends upon the number of items and their easiness range. Therefore, in designing a measurement, for example constructing a test, it will be the accuracy desired which will determine the number and easiness range of the items selected for the ability estimation.
A smaller number of items is needed to produce a given level of precision in the measurement when the difficulty level of the items is approximately equal to the ability of the person being measured. This is similar to choosing items at the fifty per cent level of difficulty in classical item analysis. For a given set of k items the standard errors of the ability estimates corresponding to raw scores around k/2 will be smaller than the standard errors for the more extreme scores near 1 and k-1. Hence, by choosing items with the appropriate difficulties it is possible to economize on the number of items administered.
Another component which makes a small contribution to the variance of ability estimates comes from the imprecision in item calibration. This effect can be made negligible by calibrating the items on large samples so that the standard errors of item estimates are very small.
An approximation of the variance of the ability estimate b* is given by:
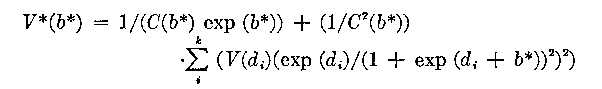 (29)
(29)
where
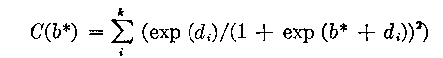
V(di ) is the variance of the item calibration di .
The first term in the right hand side of the expression (29) is due to the variance in the score and the second term is due to the imprecision of item calibration. The first term is always larger than the second. For example, if we assume that all V(di ) are one (usually V(di ) is much less than one) the second term is p(1-p) times the first. We know that the maximum value of p(1-p) is 0.25, therefore, the second term will, at the most, contribute one fourth as much variance as that due to the uncertainty in the score, in other words, at most 20 per cent of the total error variance. The magnitude of the first term depends primarily on the number of items, and to a lesser degree on the relationship between their easiness range and the ability being measured.
Given ability estimates, item estimates and their variances we can compute the standard errors of the ability estimates by means of the following FORTRAN program segment:
[obsolete source code omitted]
SA = vector of standard errors of ability estimates
K = number of items
B = vector of ability estimates
D = vector of item estimates
SI = vector of standard errors of item estimates.
D. Testing the Fit of the Item:
During item calibration it is necessary to decide whether all the items that have been tried are to be retained for the final pool. We need a statistical criterion for deciding whether an item is good enough from the point of view of the model.
To make this decision we need to investigate how the elements aji in the data matrix A depend upon the estimates di * and bj *. If we can derive the expectation E (aji ) of these elements in terms of the obtained estimates we can form a standard deviate
![]() (30)
(30)
and use this deviate as the basis for a test of item fit. If item i fits the model, and the score group rj is large enough, then yji will have an approximately unit normal distribution.
Now aji has a binomial distribution with parameters pji , the probability of making a correct response, and rj , the number of persons with a score j. Therefore, the expectation of aji is given by:
![]() (31)
(31)
and its variance by
![]()
Since bj and di are not known we use their estimates and approximate the expectation and variance of aji as
![]()
and
![]()
Examination of the matrix Y, with the standard deviates yji as elements, will show us how well the items fit, and indicate where there are signs of misfit.
From the matrix Y we can obtain statistics which will enable us to evaluate the fit of the model to the data as a whole, and we can also form approximate statistics which will help identify items which are bad, and hence need to be reconsidered. As discussed in the introduction, an item may not fit for a number of reasons. It may be badly constructed or incorrectly scored. Its discrimination may be very different from the discriminations of the other items. It could be measuring some ability other than that being measured by the rest of the items. In any case, the item will be detected so that it can be examined for deletion or revision.
The over-all statistic used in the procedure is a chi-square statistic χ2 which is obtained by summing the squared unit normal deviates over the entire matrix Y
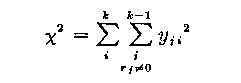 (32)
(32)
with degrees of freedom = (k-1)(m-1)
where m = number of score groups with ri ><0.
The degrees of freedom are obtained from the number of observations in the data matrix, taking account of the loss of degrees of freedom due to constraints and parameter estimation. There are k x m observations in the data matrix. There are m constraints on the score margins since sum for i=1 to k aji = jrj . Finally (k-1) item parameters have been estimated. Therefore the degrees of freedom for χ2 are:
d.f.= km -m -(k-1) (33)
= (m-1)(k-1).
An approximate χ2 statistic can also be obtained for each item by summing yji 2 over the score groups to give
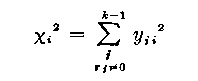 (34)
(34)
with
d.f. = m-1.
Since (34) is an approximate χi 2, we do not think it advisable to mechanically delete all items for which the χi 2 is significant at some level. We prefer to examine in detail items for which χi 2 is large. This may mean evaluating the possible effects of discrimination and guessing in these "bad" items. Then when we have decided which of the "bad" items to delete, we rerun the analysis to see how the remaining set of items look.
A FORTRAN program segment which will implement the procedure in this section is given below:
[obsolete source code omitted]
CH = mean square for the entire data.
CHI = vector of item mean squares.
R = vector of score group sizes.
M = number of occupied score groups with rj <>0.
IA = data matrix.
K = number of items.
D = vector of item estimates.
B = vector of ability estimates.
A (FORTRAN II) PROGRAM FOR SAMPLE-FREE ITEM ANALYSIS
This program estimates item and ability parameters from item analysis data according to the logistic response model:
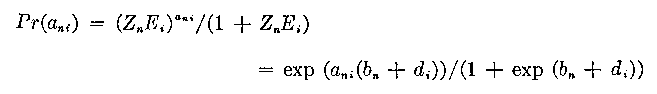
[details of obsolete computer program omitted]
REFERENCES
Gulliksen, H. Theory of Mental Tests. New York: John Wiley & Sons, 1950.
Rasch, G. Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen: Danish Institute for Educational Research, 1960. Chapters V-VII, X.
Rasch, G. An Individualistic Approach to Item Analysis. Readings in Mathematical Social Science. Edited by Lazarsfeld and Henry. Chicago: Science Research Associates Inc. 1966, 89-107. (a)
Rasch, G. An Item Analysis Which Takes Individual Differences into Account. British Journal of Mathematical and Statistical Psychology. London: 1966. Vol. 19, Part l, 49-57. (b)
Wright, B. D. Sample-Free Test Calibration and Person Measurement. Proceedings of the 1967 Invitational Conference on Testing Problems. Princeton: Educational Testing Service, 1968, 85-101.
This memo was published as: Wright, B. D., & Panchapakesan, N. (1969) A procedure for sample-free item analysis. Educational and Psychological Measurement, 29, 23-48.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo46.htm