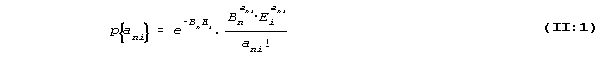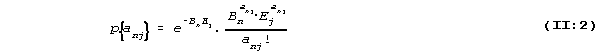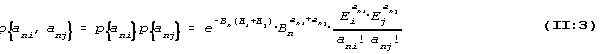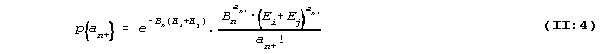The origin of the Rasch model...
Ben Wright's FOREWORD to Probabilistic Models
preceding Georg Rasch's Preface...
Probabilistic Models for Some Intelligence
and Attainment Tests is
the most important work on psychometrics since Thurstone's articles
of 1925-1929 and the 1929 monograph by Thurstone and Chave. The
psychometric research done by Rasch between 1951 and 1959, which he
explains and illustrates in this book, marks the point at which
psychometrics moved from being purely descriptive to become a
science of objective measurement. The psychometric grail of
psychological measures that transcend the questions or items
producing them was glimpsed by Thurstone in the 1920s when he set
down his requirements for valid measuring.
A measuring instrument must not be seriously affected in its
measuring function by the object of measurement. To the extent
that its measuring function is so affected, the validity of
the instrument is impaired or limited. if a yardstick measured
differently because of the fact that it was a rug, a picture,
or a piece of paper that was being measured, then to that
extent the trustworthiness of that yardstick as a measuring
device would be impaired. Within the range of objects for
which the measuring instrument is intended, its function must
be independent of the object of measurement.
(Thurstone 1928a, page 547; 1959, page 228)
Objective measurement, that is, measurement that transcends the
measuring instrument, not only requires measuring instruments which
can function independently of the objects measured, but also a
response model for calibrating their functioning, which can
separate instrument and object effects. But, because Thurstone and
his followers did not parameterize or condition for persons
individually in their response models, they never attained
objectivity. Even today there are psychometricians who try to
achieve objective measurement with methods built on samples of
normally distributed random individuals and response models that
deny parameter separation. But they fail to grasp deductions (Rasch
1968, 1977; Andersen 1973a, 1977; Barndorff-Nielsen 1978) which
show the necessity and sufficiency for objectivity of linear
logistic response models with no interaction terms. It was the
Danish mathematician, Georg Rasch, who first understood the
possibilities for objectivity that reside in the logistic response
model with one item parameter and one person parameter, and it was
Rasch who first applied this model to the analysis of mental test
data.
Georg Rasch, Doctor of Philosophy in mathematics (1930), member of
the international Statistical Institute (1941), charter member of
the Biometric Society (1947), professor of statistics (1962), and
knight of the order of Dannebrog (1967), was born in Odense,
Denmark, on 21 September 1901, the youngest and, according to his
father and himself, the "least practical" of three brothers. [I am
extremely grateful to my colleague and friend David Andrich for
these quotations. They come from an interview with Rasch which
Andrich recorded in Laesoe in June 1979, supplemented by a letter
Rasch wrote to me 5 February 1980.]
His mother was ill when he was young, and Rasch has few
recollections of her influence on his childhood. His fiercely
religious father, however, left a deep impression. Wilhelm Rasch,
sailor, ship's officer, mathematics teacher and self-appointed
missionary, was, according to his son, "one of the most hard-boiled
evangelists I have ever known."
Wilhelm Rasch moved his family to Svendborg in 1906 to open a
mission high school for prospective seamen. It was there in 1914
that Georg became fascinated by his father's forgotten trigonometry
texts and was fortunate to find a teacher who made arithmetic and
algebra, "which could so easily be extremely boring something with
which a wonderful world was opened."
The geometry behind the trigonometry did not interest Georg. But
the algebra in the trigonometric manipulations fascinated him.
Fortunately his arithmetic teacher realized that he was a born
mathematician and persuaded his father, despite the extra expense,
to send Georg to the cathedral school in Odense where there was a
curriculum specializing in mathematics arid science. He enrolled
there in 1916 and in 1919 graduated and went to the University of
Copenhagen.
In Copenhagen I entered the Faculty of Science, to which
mathematics belonged, and got into immediate contact with my
teachers. I had, of course, to learn the elements of function
theory and even geometry, but I concentrated upon the analytic
part which I liked. My first professor lectured on functions,
algebra, and number series.... Although I worked for him on
his numerical studies, what caught my interest was the theory
of Lagrange equations. That resulted in my first publication,
a joint paper by my professor and myself (Neilsen and Rasch
1923)....
I got a stipend for my further studies and became a member of
college Regensen, where we received free room and board. When
I got the stipend I did not see any further reason for doing
arithmetical work for my earnings, so I left Professor Neilsen
and got another teacher, Professor Nørlund, who had written an
extremely good book on difference equations. Nørlund was my
professor for the rest of my time as a student, and I was his
assistant teacher from 1925, when I graduated, until 1940. The
topics in function theory that Nørlund lectured about together
with the other topics I had to study in order to lecture as
his assistant built up my mathematical background.
Nørlund was also the director of the Geodetic Institute ... to
which I became attached to provide mathematical and
computational assistance. This added to my income and in
February 1928, 1 married my sweetheart, Elna Nielsen, with the
charming call-name of Nille. Two daughters were added to the
family in 1931 and 1933.
My thesis, which I defended in 1930, was the fruit of my
cooperation with Nørlund, but in a field which he himself did
not cultivate at the time. It dealt with matrix algebra and
its applications to the theory of linear systems of difference
and differential equations. I have always loved to think, but
I have never been inclined to do extensive reading and so I
had never seen anything about matrices. Nørlund gave lectures
on systems of difference equations in which he wrote out every
equation in detail every time. When working through my notes
I discovered, to my surprise, that these long equations could
be condensed in a very simple way. I did not know anything
about matrices at that time, but just invented them for myself
and discovered what their rules must be. Only later did I find
out that others had already formalized the idea.
So I invented my own theory of matrices, especially as they
applied to linear systems of difference and differential
equations of first order. The ... part of my thesis on the
theory and application of product integrals which developed
the solution of a linear system of differential equations as
a generalization of the ordinary elementary integral was
published in German (Rasch 1934). Many years later I learned
that the techniques developed in this paper played a part in
solving some problems in atomic theory and were also used to
prove some difficult theorems in group theory. I mention this
to point out that, although I have been known as a
statistician, my original talent, if I had any, must have been
in mathematics.
The early 1930s were difficult for Rasch. Aside from teaching as
Nørlund's assistant and some small matters in the seismic division
of the Geodetic Institute, there was no work in mathematics. Rasch
had, however, two medical acquaintances studying the reabsorption
of cerebrospinal fluid in monkeys. Helping them to understand their
data gave him his first practical experience with the exponential
distribution and material for his first experimental paper (Fog,
Rasch, and Stürup 1934).
The success of this collaboration encouraged Fog and Stürup to
engage Rasch to teach a small group of psychiatrists and
neurologists some elementary mathematics and statistics. Word of
this got to the head of the Hygienic Institute, who was also
interested in statistics. The outcome was that Rasch served the
Hygienic Institute as statistical consultant from 1934 to 1948 and
also become attached to the State Serum Institute, a relationship
which continued until 1956.
About the same time Nørlund, for whom Rasch still taught
mathematics, and Madsen, the director of the Serum Institute got
into a conversation about him at a meeting. They agreed that, in
order to do his job at the Serum Institute, he needed to learn the
latest developments in statistics. One of them knew about R. A.
Fisher, so they applied to the Rockefeller Foundation for a year's
study with Fisher in London.
The Rockefeller fellowship was granted, but, while it was brewing,
Rasch went to Oslo for three months on a Carlsberg grant to study
Ragnar Frisch's confluence analysis, a technique developed for
economics, but similar to Thurstone's factor analysis. Then, in
September 1934, Rasch joined Fisher's staff at the Galton
Laboratory in London.
I went through Fisher's statistical methods and learned the
kind of chi-squares ... be used.... I soon got hold of his
1922 paper where he developed his theory of maximum
likelihood, because I was especially interested in that
matter. What caught my interest most was his idea that this is
a form of generalization of just the same kind as Gauss
attempted when he invented the method of least squares.
The meaning of least squares is not, in Fisher's
interpretation, just a minimization of a sum of squares. It is
a maximization of the probability of the observations,
choosing such values as estimates of the parameters as will
maximize the probability of the set of observations at your
disposal. There is a very essential difference between this
and the simple idea of minimizing sums of squares. This
philosophy went further when Fisher got to his concept of
sufficiency....
To purely mathematical minds sufficiency may appeal as nothing
more than a surprising and singularly nice property, extremely
handy when accessible, but, if not, then you just do without
it. But to me sufficiency means much more than that. When a
sufficient estimate exists, it extracts every bit of knowledge
about a specified feature of the situation made available by
the data as formalized by the chosen model. 'Sufficient'
stands for 'exhaustive' as regards the feature in question.
What is left over when a sufficient estimate has been
extracted from the data is independent of the trait in
question and may therefore be used for a control of the model
that does not depend on how the actual estimates happen to
reproduce the original data. This is a cornerstone of the
probabilistic models that generate specific objectivity.
The realization of the concept of sufficiency, I think, is a
substantial contribution to the theory of knowledge and the
high mark of what Fisher did.... His formalization of
sufficiency nails down the ... conditions that a model must
fulfill in order for it to yield an objective basis for
inference.
During his year in London, Rasch also discussed the problem of
relative growth with Julian Huxley. Using data on crab shell
structure, Rasch had discovered that it was possible to measure the
growth of individual crabs as well as populations. His
conversations with Huxley convinced him that this was the line of
research he wished to follow. "It meant quite a lot to me to
realize the meaning and importance of dealing with individuals and
not with demography. Later I realized that test psychologists were
not dealing with the testing of individuals, but ... were studying
how traits, such as intelligence, were distributed in populations.
They were making demographic studies and not studies of
individuals."
Rasch began teaching statistics to biologists in the fall of 1936,
but not until 1938 did he come into professional contact with
psychologists. Another friend, Rasmussen, worked at the
Psychological Laboratory at the University of Copenhagen, where
there happened to be a six month vacancy. When the director,
Professor Rubin, heard of Rasch's interest in statistics, he asked
him to give a few lectures to the psychologists. This connection
lasted for thirty years.
The war interfered with further developments, but in 1944 a program
in educational psychology was begun at the laboratory and Rasch was
engaged to teach statistics. This aroused his interest in the
multivariate normal distribution and led him to an elegant proof of
Wishart's theorem (Rasch 1948).
Meanwhile, a friendship with Chester Bliss made in London in 1935
brought Rasch to the United States in 1947 to participate in the
founding of the Biometrics Society (Rasch 1947a) and in the postwar
reorganization of the International Statistical Institute in
Washington. In the course of these meetings Tjalling Koopmans, a
fellow student of Ragnar Frisch's confluence analysis and Fisher's
sufficient statistics, invited Rasch to spend two months with the
Coles Commission on Economic Research at the University of Chicago,
where he met L. J. Savage. This set the stage for Savage to bring
Rasch back to Chicago in 1960, to finish writing Probabilistic
Models and to give the series of lectures that introduced this
writer to Rasch's new psychometrics.
Rasch began his work on psychological measurement in 1945 when he
helped Rubin and Rasmussen standardize an intelligence test for the
Danish Department of Defense (Rasch 1947b). But,
the big event came in 1951 when the Minister of Social Affairs
wanted to know whether the kind of extra education given to
poor readers had any effect that endured. Children who had
been to school in the 1940's were now around twenty years old.
They were retested for reading capability a number of times.
By comparing scores I could draw some conclusions about the
development of each individual student. But that work was very
imperfect. One of my collaborators collected a set of data
from 125 children, where each had been followed for five
years. Each year they were tested one or two times for their
reading ability. I thought there should be some kind of
developmental study in that. When I got the data I made the
guess that it might be a good idea to try the multiplicative
Poisson model. It turned out that it fitted the data quite
well.
The next essential event was in 1953, when Borge Prien
constructed an intelligence test consisting of four parts.
Each of the parts were constructed to be closely conformable
to the multiplicative model for dichotomous items. The
discovery of that model occurred in connection with my
analysis of the reading tests. I had chosen the multiplicative
Poisson for the reading tests because it seemed a good idea
mathematically, if it would work. It turned out that it did.
Then I wanted to have some motivation for using it, and not
only the excuse that it worked. In order to do so, I imitated
the proof of a theorem concerning a large number of
dichotomous events, each of them having a small probability.
Under conditions which can be specified easily, including that
these probabilities be small, the number of events becomes
Poisson distributed. I imitated that proof, but in doing so I
took care that the imitation ended up with the multiplicative
Poisson model, that is, I made sure that there was a personal
factor entering into each of the small probabilities for the
dichotomous outcome. The probabilities for the dichotomous
case should therefore be of the form L/(1+L), and the L would
have a factor that was personal through all of the items and
each item, of course, would have its own parameter and then I
had my new model.
I had taken a great interest in intelligence tests while
working with Rubin and Rasmussen in 1945. It struck me that I
might analyze the test we had constructed then, and which had
been taken over by the Military Psychology Group. I tried to
see whether the model worked there and also whether it worked
in some other tests. The first thing I did ... was to analyze
the Raven tests. They worked almost perfectly according to the
multiplicative model for dichotomous items. That was my first
nice example using the newly discovered model. Now I compared
the results of the Raven's test and the results of my analysis
of the military intelligence test. The intelligence test did
not conform.
When I showed this to the head of the military psychologists
he immediately saw the point. I had talked to him about my
attempts to make sense of intelligence tests by means of the
model I had discovered in connection with the multiplicative
Poisson. And I had also told him about the Raven's tests. But
now I presented the examination of the test he actually had in
current use from the Psychology Laboratory. I pointed out to
him that it would seem to consist of different groups of items
with quite different kinds of subject matter. His immediate
reaction was to call on Borge Prien who was working for the
military psychologists and to give him the order that, within
the next six months, before the next testing session in
November 1953, to have ready a new intelligence test
consisting of four different subtests, each of these to be
built in such a way that they followed the requirements that
Rasch demanded.
It was remarkable. Prien did that in six months. He invented
tests, which, when you see them, are rather surprising. He
really did invent items of the same sort, from very easy to
very difficult, and spaced in a sensible way. We did do some
checking in the process and omitted or modified items that did
not seem to be working. It was really a masterpiece. Prien had
been told, 'All you have to construct is four different kinds
of tests, with very different subject matters and each of them
should be just as good as Georg tells us that Raven's tests
are.' And he did so. That was when I really began to believe
in the applicability of that elementary model.
In 1957 I gave ... some free lectures on the researches I had
done since Prien's construction of the new intelligence tests.
I told about the multiplicative Poisson and about the nice
little model which sorts items out from each other. My
lectures were tape-recorded, and my daughter Lotte got the
task of deciphering them and writing them down. She made a
proper work out of it, and what she did was taken over by the
Educational Institute, and they had it mimeographed.
At that time the institute consisted of five different
departments, each with its own head. Every Friday morning the
company of them, together with the director, Erik Thomsen, and
I had a meeting where we discussed current matters. Thomsen
organized it so that on a number of these Fridays we went
through my manuscript. That was very good for it. It clarified
many points that I had been vague about. I was forced by the
young fellows there to make it quite clear what I really
meant.
By 1953 Rasch had used a Poisson model to analyze a family of oral
reading tests and with Borge Prien had designed and built a
four-test intelligence battery fitting the requirements of his
logistic model for item analysis. Rasch discussed his concern about
sample dependent estimates in an article on simultaneous factor
analysis in several populations (Rasch 1953). However, his work on
item analysis remained unknown outside Denmark until 1960, when he
lectured in Chicago, gave a paper at the Berkeley Symposium on
Mathematical Statistics (Rasch 1961), and published Probabilistic
Models.
In her 1965 review of person and population as psychometric
concepts, Jane Loevinger wrote,
Rasch (1960) has devised a truly new approach to psychometric
problems.... He makes use of none of the classical
psychometrics, but rather applies algebra anew to a
probabilistic model. The probability that a person will answer
an item correctly is assumed to be the product of an ability
parameter pertaining only to the person and a difficulty
parameter pertaining only to the item. Beyond specifying one
person as the standard of ability or one item as the standard
of difficulty, the ability assigned to an individual is
independent of that of other members of the group and of the
particular items with which he is tested; similarly for the
item difficulty.... Indeed, these two properties were once
suggested as criteria for absolute scaling (Loevinger, 1947);
at that time proposed schemes for absolute scaling had not
been shown to satisfy the criteria, nor does Guttman scaling
do so. Thus, Rasch must be credited with an outstanding
contribution to one of the two central psychometric problems,
the achievement of non-arbitrary measures. Rasch is concerned
with a different and more rigorous kind of generalization than
Cronbach, Rajaratnam, and Gleser. When his model fits, the
results are independent of the sample of persons and of the
particular items within some broad limits. Within these
limits, generality is, one might say, complete.
(Loevinger 1965, page 151).
In Rasch's words:
In the beginning of the 60's I introduced a new-or rather a
more definite version of an old-epistemological concept. I
preserved the name of objectivity for it, but since the
meaning of that word has undergone many changes since its
Hellenic origin and is still, in everyday speech as well as in
scientific discourse, used with many different contents, I
added a restricting predicate: specific.
Let it be said at once: my professional background is
mathematical and statistical, not philosophical. The concept
has therefore not been carved out in a conceptual analysis,
but on the contrary its necessity has appeared in my practical
activity as a statistical consultant for about 30 years and in
the later years as a professor of Theoretical Statistics with
Reference to its Applications to the Social Sciences.
During these activities I was introduced to very diverse
subjects: medicine and hygiene with the connected parts of
biology; psychology and education; technology; economics;
demography and sociology: linguistics; etc. In spite of the
diversity of subjects the analytic methods generally available
were rather limited for the first many years. But in 1951 I
was faced with a task the solution of which added a new tool
to my arsenal.
In that year The Danish Ministry of Social Affairs wanted an
investigation of the development of reading ability in 125
then about 20 years old former students of public schools in
Copenhagen, who in their school years had suffered from
serious reading difficulties and therefore had received
supplementary education in that discipline.
For each of these students were recorded the results of
repeated oral reading tests during his school years-both as
regards reading speed and reading accuracy as well as of a
test at an after-examination late in 1951.
It would be a fairly simple task to follow the development of
a student's reading ability over a number of years if the same
part of the same test were used every time, but at each
testing it was necessary to choose a test which corresponded
approximately to his standpoint, so as a rule a student was
followed up with a series of tests of increasing "degrees of
difficulty".
In a concrete formulation of this problem I imagined-in good
statistical tradition-the possibility that the reading ability
of a student at each stage, and in each of the two
above-mentioned dimensions, could be characterized in a
quantitative way-not through a more or less arbitrary grading
scale, but by a positive real number defined as regularly as
the measurement of a length.
Whether this would be possible with the tests in question
could not be known in advance. it had to be tried out through
a separate experiment which was carried out in January 1952.
In this experiment about 500 students in the 3rd-7th school
year were tested with 2 or 3 of the texts used in the
investigation of students with reading difficulties.
(Rasch 1977, pages 58-59)
Rasch develops his seminal analysis of these reading data in
chapters I through IV of Probabilistic Models. Not only is his
discussion easy to follow and to learn from, but it allows one to
participate in the implementation of a decisive step in
psychometric method. These four chapters describe the dawn of a new
era in psychometric theory and practice.
The outcome of the reading test experiment was beyond
expectation: a statistically very satisfactory analysis on the
basis of a new model which represented a genuine innovation in
statistical techniques!
But the understanding of what the model entails tarried
several years. At the 1959 anniversary of the University of
Copenhagen the highly esteemed Norwegian economist Ragnar
Frisch - later Nobel Prize winner - was to receive an honorary
doctorate. I visited him by appointment the next day, and when
our business was finished he asked me what I had been doing in
the 25 years since I stayed at his institute in Oslo for a
couple of months to study a new technique of statistical
analysis that he had developed.
As mentioned I had been doing some very varied things, but I
soon concentrated on the comparison of reading abilities, one
of the topics of a monograph which I was then preparing.
On this occasion I did not mention reading errors, but rather
the students' reading speeds. The model is, however, the same:
the Multiplicative Poisson Model which I then proceeded to
explain to Ragnar Frisch in the following way:
Applied to reading speed the model states that the probability
that person no. n in a given time reads ani, words of text no.
i is determined by the Poisson distribution
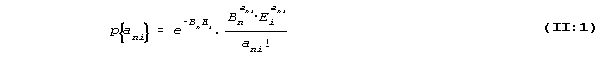
where a high value of the parameter Lni = Bn.Ei means that many
words are read in the given time, and thus a high value of Bn
means high reading speed and a large value of Ei means a text
which is quickly read, thus in this respect an easy reading
test.
Likewise the probability that the person reads anj words of
test no. j under similar conditions is
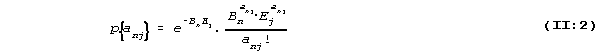
It is also assumed that the actual results of test no. i, ani
has no influence on the probabilities of the possible outcome
of the other test. The multiplication rule for probabilities
in these conditions says that the probability of the outcomes
ani and anj of the two tests is the product of the two
probabilities (II: i) and (11:2) thus
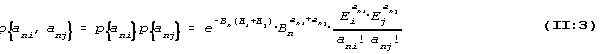
The Poisson distribution has the property (which in fact can
be derived from (II:3)) that the sum of the two Poisson
distributed variables is also Poisson distributed with a
parameter which is the sum of the two parameter values. With
the notation an+ for the sum ani + anj, we then have
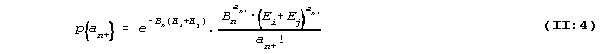
At this stage we apply another basic rule of the calculus of
probabilities which in this context can be formulated thus: In
the class of possible outcomes where the total number of words
read, an+, has a fixed value, the probability of the outcomes
ani and anj conditional on this total, is given by dividing
(11:4) into (II:3).
Until now the non-mathematical reader has been advised to skip
the formulas (and until this point Frisch had only listened
politely), but now I shall present a crucial point which
demands a careful inspection of the two last formulas, but not
necessarily an understanding of their content:
On the right side Of (II:3) and (II:4) the person parameter Bn
appears in exactly the same [way in the] two expressions,
namely in the exponential function of the same argument:

and raised to the same power:

When (II:4) is divided into (II:3) these two factors both
cancel out, and the resulting conditional probability does not
contain the person parameter Bn; the probability that the
given number of words read, an+, is composed of ani and anj
words of the two tests is expressed by
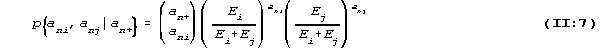
which is determined by the observed numbers ani and anj and by
the ratio between the difficulty parameters of the two tests,
while it is not influenced by which person involved. On seeing
(II:7) Frisch opened his eyes widely and exclaimed: "It (the
person parameter) was eliminated, that is most interesting!"
And this he repeated several times during our further
conversation. To which I of course agreed every time - while
I continued reporting the main results of the investigation
and some of my other work.
Only some days later I all of a sudden realized what in my
exposition had caused this reaction from Ragnar Frisch. And
immediately I saw the importance of finding an answer to the
following question: "Which class of probability models has the
property in common with the Multiplicative Poisson Model, that
one set of parameters can be eliminated by means of
conditional probabilities while attention is concentrated on
the other set, and vice versa?"
What Frisch's astonishment had done was to point out to me
that the possibility of separating two sets of parameters must
be a fundamental property of a very important class of models.
(Rasch 1977, pages 63-66)
It is the two earliest and most popular members of this "very
important class of models" which Rasch presents and applies in
Probabilistic Models. Although the book focuses on the measurement
of reading accuracy, speed, and intelligence, the basic principles
employed are fundamental to all scientific work.
When first suggesting the models (for measuring) I could offer
no better excuse for them than their apparent suitability,
which showed in their rather striking mathematical properties.
In Rasch (1961) a more general point of view was indicated,
according to which the models were strongly connected with
what seemed to be basic demands for a much needed
generalization of the concept of measurement.
In continuation of that paper my attention was drawn to other
fields of knowledge, such as economics, sociology, history,
linguistics, evaluation of arts, etc. where claims are arising
of being taken just as seriously as Natural Sciences.
On a first sight the observational material in Humanities
would seem very difficult from that in physics, chemistry and
biology, not to speak of mathematics. But it might turn out
that the difference is less essential than it would seem. In
fact, the question is not whether the observations are of very
different types, but whether Sciences could be firmly
established on the basis of quite different types of
observation.
(Rasch 1967)
The psychometric methods introduced in this book go far beyond
measurement in education or psychology. They embody the essential
principles of measurement itself, the principles on which
objectivity and reproducibility, indeed all scientific knowledge,
are based.
References:
Andersen, E. B. 1973a. Conditional Inference and Models.for
Measuring. Copenhagen: Mentalhygiejnisk Forlag. 1973 b. A goodness
of fit test for the Rasch model. Psychometrika 3 8: 123-40.
1977. Sufficient statistics and latent trait models. Psychometrika
42: 69-81.
Barndorff-Nielsen, 0. 1978. Information and Exponential Families in
Statistical Theory. New York: John Wiley and Sons.
Loevinger, J. 1947. A systematic approach to the construction and
evaluation of tests of ability. Psychological Monographs 61.
Loevinger, J. 1965. Person and population as psychometric concepts.
Psychological Review 72: 143-55.
Rasch, G. 1923. Notes on the equations of Lagrange (with N.
Nielsen). Det. kgl. Danske videnskabernes selskab.
Mathematisk-fysiske meddelelsev 5, no. 7: 1-24.
1934. On Matrix Algebra and Its Application to Difference and
Differential Equations. Copenhagen.
1934. On the reabsorption of cerebrospinal fluid (with M. Fog and
G. Stürup). Skandinavischen Archiv für Physiologie 69: 127-50.
1947a. Recent biometric developments in Denmark. Biometrics 4:
172-75.
1947b. On the evaluation of intelligence tests. Kobenhavns
Universitets psykologiske Laboratorium.
1948. A functional equation for Wishart's distribution. Annals of
Mathematical Statistics 19: 262-66.
1953. On simultaneous factor analysis in several populations.
Uppsala Symposium on Psychological Factor Analysis. Nordisk
Psykologi's Monograph Series 3: 65-71, 76-79, 82-88, 90. Uppsala.
1960. Probabilistic Models for Some Intelligence and Attainment
Tests. Copenhagen: Danish Institute for Educational Research.
1961. On general laws and meaning of measurement in psychology.
Proceedings of the Fourth Berkeley Symposium on Mathematical
Statistics and Probability 4: 321-33. Berkeley: University of
California Press.
Rasch, G. 1966b. An item analysis which takes individual
differences into account. British Journal of Mathematical and
Statistical Psychology 19: 49-57.
1967. An informal report on the present state of a theory of
objectivity in comparisons. In Proceedings of the NUFFIC
International Summer Session in Science at "Het Oude Hof." L. J.
van der Kamp and C. A. J. Viek, eds. Leiden.
1968. A mathematical theory of objectivity and its consequences for
model construction. In Report from European Meeting on Statistics,
Econometrics and Management Sciences. Amsterdam.
1969. Models for description of the time-space distribution of
traffic accidents. Symposium on the Use of Statistical Methods in
the Analysis of Road Accidents. Organization for Economic
Cooperation and Development Report No. 9.
1972. Objektvitet i samfundsvidenskaberue et metodeproblem.
Nationalekonomisk Tidsskrift 110: 161-96.
1977. On specific objectivity: An attempt at formalizing the
request for generality and validity of scientific statements.
Danish Yearbook of Philosophy 14: 58-94.
Thurstone, L. L. 1925. A method of scaling psychological and
educational tests. Journal of Educational Psychology 16: 433-51.
1926. The scoring of individual performance. Journal of Educational
Psychology IT 446-57.
1927. The unit of measurement in educational scales. Journal of
Educational Psychology 18: 505-24.
1928a. Attitudes can be measured. American Journal Of Sociology 33:
529-54 (In L. L. Thurstone, ed. 1959. The Measurement of Values,
pp. 215-33. Chicago: University of Chicago Press.)
1928b. The measurement of opinion. Journal of Abnormal and Social
Psychology 22.: 415-30 (In Thurstone, Measurement of Values, pp.
234-47).
1929. Theory of attitude measurement. Psychological Review 36:
222-41 (In Thurstone, Measurement of Values, pp. 266-8 r).
Thurstone, L. L., and Chave, E.J. 1929. The Measurement of
Attitude. Chicago: University of Chicago Press.
From: The Foreword by Benjamin D. Wright to Georg Rasch's
"Probabilistic Models for Some Intelligence and Attainment Tests",
Chicago: University of Chicago Press, 1980; MESA Press, 1992.
Georg Rasch's PREFACE to Probabilistic Models
For several years statistical methods have been a favorite
instrument within various branches of psychology. Warnings have,
however, not always been wanting. Two instances from recent
literature may serve as examples.
Skinner1 vigorously attacks the application of statistics in
psychological research, maintaining that the order to be found in
human and animal behavior should be extracted from investigations
into individuals, and that psychometric methods are inadequate for
such purposes since they deal with groups of individuals.
As far as abnormal psychology is concerned Zubin2 expresses a
similar view in stating: "Recourse must be had to individual
statistics, treating each patient as a separate universe.
Unfortunately, present day statistical methods are entirely
group-centered so that there is a real need for developing
individual-centered statistics."
Individual-centered statistical techniques require models in which
each individual is characterized separately and from which, given
adequate data, the individual parameters can be estimated. It is
further essential that comparisons between individuals become
independent of which particular instruments tests or items or other
stimuli - within the class considered have been used.
Symmetrically, it ought to be possible to compare stimuli belonging
to the same class - "measuring the same thing" - independent of
which particular individuals within a class considered were
instrumental for the comparison.
This is a huge challenge, but once the problem has been formulated
it does seem possible to meet it. The present work demonstrates, by
way of three examples from test psychology, certain possibilities
for building up models meeting these demands. And it would seem
quite possible to modify and extend the methods used here to cover
much larger areas, but in order to investigate how far the
principles go - and what should be done outside possible limits -
much research is needed. it is hoped, however, that planned
continuations of the present work and contributions from others
will gradually enlarge the field where fruitful models can be
established.
In part A, chapters I-VII, I have tried to discuss the basic
principles rather carefully, using only the amount of mathematics
that I deemed necessary - mathematical models can hardly be
adequately presented quite without mathematics. In the same
chapters the reader will find a rather detailed numerical
and graphical documentation which may, I hope, serve as a useful
guide for others in analyzing their own suitable data from similar
fields. I should be very grateful for information about such
studies, carried out or being planned.
In part B, chapters VIII-X, a fairly full account is given of the
mathematical background, extended, however, for the sake of
completeness, to cover some more ground than has actually been
utilized in part A.
Psychologists wishing to use the methods in practice will miss a
careful discussion of how to do so. I consider, however, that it is
as yet a little early to go right ahead to practice. For one thing,
the work presented here needs corroboration from other sources
where different, but related test batteries have been applied to
other groups of people, before even the fields approached here may
be regarded as safely covered. And furthermore the gain is very
modest if we only master a tiny corner out of the vast fields of
test psychology, not to speak of other fields of psychology. I
therefore feel an urgent need for investigations on a rather large
scale and covering a wide range before we turn the methods thus
acquired into, as it were, technological use.
The work presented in this book has grown out of practical tasks
assigned to me as a consultant.
In 1945-1948 I analyzed data collected by the Department of
psychology at the University of Copenhagen with a view to a
standardization of a new group intelligence test of the omnibus
type, to be used by the Department of Defense in personnel
selection. In carrying out the item analysis I became aware of the
problem of defining the difficulty of an item independently of the
population and the ability of an individual independently of which
items he had actually solved.
In 1952 the Department of Social Welfare wanted a follow-up study
carried out on a group of juveniles, 20 years old, which at school
had attended special reading classes, because of reading
retardation. This task resulted in the two models developed in
chapters II and III, implying unambiguous definitions of ability
and difficulty in connection with oral reading tests.
Towards the end of 1952 I became connected with the newly
established Psychological Service Group of the Defense
[Department]. A reanalysis of the omnibus intelligence test
mentioned above was based upon the recently discovered model of
simple conformity (cf. chapter V and chapter VII, 12) and induced
the construction of a new group intelligence test (BPP) consisting
of four subtests, each designed to yield a measurement of a
specific ability as in introduced through the model. The analysis
of subsequently collected data, demonstrated in chapter VI, shows
how far the construction succeeded and where it failed.
The establishment in 1955 of the Danish Institute for Educational
Research brought me a wealth of problems requiring clarifications,
elaborations and extensions of the principles already laid down,
the influence of which process pervades all the book.
In my attempts to provide for statistical tools pertaining to the
psychological problems in question I have of course profited
greatly from cooperation and from numerous discussions with many
psychologists, too many to be named here.
The foundation, however, was laid in connection with my first
mentioned work, through penetrative discussions with the late
professor Edgar Rubin and his colleague E. Tranekjaer Rasmussen,
which I shall always recall with deep gratitude.
For the provision of conditions, necessary for coordinating my
unorthodox research with the practical consultative work wanted by
them I extend my sincere thanks to the institutions mentioned.
In particular I wish to express my gratitude to Major Poul Borking,
M.A., head of the Psychological Service Group of the Defense in the
period 1952-1956, and to Erik Thomsen, M.A., director of the Danish
Institute for Educational Research, for the keenness with which
they have at any time been ready to discuss my views, both
theoretically and in their practical implications, and try to find
means for carrying out my suggestions.
One of the consequences has been that in the final phase of my work
I have had the privilege of drawing heavily upon the Institute. In
particular I have utilized the facilities of the Department of
Statistics with the leader of which, G. Leunbach, M.A., I have had
a most fruitful cooperation since his appointment in 1956.
A preliminary Danish edition of the manuscript was carefully
scrutinized by the staff members of the Institute.
The Danish text was translated - or rather transformed - into
English by G. Leunbach, who has also revised later additions in
English.
L. J. Savage of the University of Chicago has kindly read the final
manuscript critically.
For all improvements to which the book has thus been subjected I am
very thankful.
The publication of this work, nothing of which has previously been
accessible outside a restricted circle, has been rendered possible
by the generosity of the Institute. Thanks to that, this volume
presents a lavishness of documentation - tables and graphs - which,
although much needed, is nowadays not often seen in scientific
publications.
The Danish Institute for Educational Research.
February 1960.
G. Rasch.
1. B. F. Skinner, A Case History in Scientific Method. The American
Psychologist 11 (1956), p. 221-33.
2. J. Zubin et al., Experimental Abnormal Psychology. Columbia
University Store. New York 1955. Mimeographed. - p. 2-28.
From: The Preface by Georg Rasch to his "Probabilistic Models for
Some Intelligence and Attainment Tests", Chicago: University of
Chicago Press, 1980; MESA Press, 1992.
Editor's Preface to 1960 Edition
Danmarks paedagogiske Institut
Studies in Mathematical Psychology I
G. Rasch
Probabilistic Models for Some Intelligence and Attainment Tests
1960
The Danish Institute for Educational Research
101 Emdrupvej, Copenhagen NV, Denmark, SOborg 8808
Printed by Nielsen & Lydiche (M. Simmelkiaer), Copenhagen
Editor's Preface
With this monograph by our consultant, G. Rasch, Ph.D., the Institute
opens a series of publications for which it has chosen the title of
Studies in Mathematical Psychology.
We hope in this series to be able to publish as well monographs
as reprints of articles by our staff members, all under the cover
which has been designed for the publications of the Institute. We
believe that this first issue of the series has pointed to problems
of very general importance, and we hope in further contributions
to be able to elucidate the problems from other sides.
Erik Thomsen
Director
Go to Top of Page
Go to Institute for Objective Measurement Page