Extreme Raw Scores are Biased against Measures: Floor and Ceiling Effects
All measures are numbers. But not all numbers are measures.
Some numbers, like car licenses, are merely labels. Others, like Room #215, name a location. It may help us find Room #215. But it does not tell us how many steps it takes to get there.
Other numbers come as counts, scores and ranks, like 10 hospital days, 17 PECS© rating scale points and 3rd place. Because we get these numbers by direct observation, they have the reality of being seen to occur. As a result these kinds of numbers are often mistaken for measures and then misused in statistical analyses for which they are quite unsuited.
Counts, scores and ranks do not qualify as measurements because the very "reality" of the concrete units counted guarantees that their relevance to our reason for counting them cannot be uniform. Some "days" are worth more than others. How far is it from 1st to 2nd place?
Finally, there are the numbers that deserve to be called "measures". These are counts of abstract generic units, like 3000 dollars, 99 degrees and 50 pounds. Each unit is a perfect idea which can only be approximated in practice. But its good-enough-for-practice approximation is what produces the kind of numbers which make the work of physical scientists, engineers, architects, businessmen, tailors and cooks useful and productive. Genuine "measures" and not mere "scores" are the kind of numbers we need for outcome evaluation.
When we use numbers to compare outcomes, we do arithmetic with them. We add and divide to compute means. We subtract to compare alternatives and gauge improvements. We calculate rates of change to estimate costs and weigh the effects of exposure and treatment.
Arithmetic done with numerical labels makes nonsense. As we proceed we will see that arithmetic done with counts, scores and ranks can also be tragically misleading. We must learn how to transcend this problem by the routine application of a simple mathematical model which constructs abstract linear measures from the concrete raw data for which counts, scores and ranks are the media. For the arithmetic of statistical analysis to be useful, it must be done with equal interval, constant unit, linear measures. Nothing else will do!
Which Numbers are Measures?
How can we tell the difference between numbers which are measures and numbers which are not? Measures are the kind of numbers that cooperate with arithmetic, can be added and subtracted, multiplied and divided. No one using numbers as labels, like license plates, would think of doing arithmetic with them, except as a joke.
The second use of numbers as counts, scores and ranks, however, does tempt many to do arithmetic. Ratings mark out an order of increase. There is usually little doubt that a rating of two is meant to mean more than a rating of one and also less than a rating of three. The question unanswered by ratings is not which is more but, from the point of view of actually doing arithmetic: How much more? How much less?
We may be able to believe in the rank order of ratings. Indeed, the best of our incoming raw data are no more than ratings. But, if we are realistic about the situation, we have to admit that our ideas about the spacing between ratings are vague. We may feel sure that a rating of two is more than a rating of one. But we do not know how much more. As we think this over we are bound to realize that even though ratings specify order, they do not have the numerical properties necessary to serve arithmetic. Subtractions of ratings are meaningless. So are sums of ratings and hence also averages and standard deviations of ratings.
Another kind of observed number, the raw score, is often misused as though it were a measure because it is a count of what amount to ratings. But counting does not make raw scores any better for arithmetical analysis that the ratings counted. When we add raw scores we are counting "right" answers. But there is no reason at all to suppose that the right answers counted are all the same size.
This realization is far from recent. In 1904 the founder of educational measurement, American psychologist Edward Thorndike, observed:
If one attempts to measure even so simple a thing as spelling, one is hampered by the fact that there exist no units in which to measure. One may arbitrarily make up a list of words and observe ability by the number spelled correctly. But if one examines such a list one is struck by the inequality of the units. All results based on the equality of any one word with any other are necessarily inaccurate. (1904, p.7)
Thorndike saw the unavoidable ambiguity in counting concrete events, however indicative they might seem. One might observe signs of spelling ability. But one would not have measured spelling, not yet (Engelhard 1984, 1991, 1994). The problem of what to count, that is, entity ambiguity, is ubiquitous in science, commerce and cooking. What, come to think of it, is an apple? How many little apples make a big one? How rotten can an apple be and still get counted? Why don't three apples always cost the same amount? With apples, we solve entity ambiguity by renouncing the concrete apple count and turning, instead, to abstract apple volume or, better still, apple weight (Wright 1992, 1994). This ambiguity as to the value of what is being counted makes raw scores unsuited to the arithmetic so mistakenly done with them.
What kind of numbers, then, are good enough to do arithmetic with? Only numbers that approximate the idea of a perfectly uniform unit which makes a difference of one between any two numbers always mean exactly the same amount. Only then can we do arithmetic with the numbers. Only then can we make sense of means and standard deviations. Only then do we have numbers good enough to use as measures.
But numbers like that do not occur naturally. Their perfection is only an idea, an abstraction, a triumph of imagination. To obtain actual values for such numbers we must invent devices which produce good-enough approximations of our "perfect" units to be useful. The yardstick is the canonical example. We are content to use the inch marks on most yardsticks as though they were perfectly spaced at exactly one inch apart. We know, of course, that were we to look closely we could prove beyond a shadow of a doubt that the inch marks on any particular yardstick vary slightly in their spacing. Do we then abandon the yardstick? Absolutely not! All we require is that the inch mark spacings approximate uniformity well enough to keep the yardstick useful as a device for measuring length, say to the nearest inch.
Many social scientists are confused about the difference between ratings, raw scores and measures. They mistake ordinal ratings and scores for measures and attempt to understand their data by linear analyses of these ordinal values. Their results are inevitably ambiguous in arbitrary ways which remain unknown to these researchers. Little wonder that there is so much confusion and contradiction and so little progress in contemporary social science. Outcome measurement cannot afford to suffer this foolish mistake.
The mistake is completely unnecessary. There is a simple, efficient and easily applied method for constructing good approximations of abstract measures from concrete ordinal observations like raw scores and ratings. This chapter discusses the unavoidable ambiguities in data collection, provides understanding of the ways in which raw scores and Likert scales are misleading when mistaken for measures, explains how raw, concrete observations like ratings can be used to construct outcome measures and gives some examples of the useful maps and scoring forms which follow from the construction of measures.
Ratings
To measure treatment outcomes, we rate patients' typical functional independence on typical tasks of daily living according to scales like:
1 - Maximally Dependent
2 - Moderate Assistance
3 - Minimal Assistance
4 - Requires Supervision
5 - Limited Independence
6 - Functional Independence
7 - Fully Independent
When we use these ratings to evaluate a patient, we presume that we:
a - Judge the patient correctly,
b - According to reproducible criteria,
c - With ratings accurately recorded,
d - In terms of uniformly spaced levels like 1,2,3,4,5,6,7,
e - Which add up to scores as good as measures.
But our presumptions are naive. Our ratings are no better than:
a'- Educated guesses,
b'- According to fluctuating personal criteria,
c'- Not always recorded correctly,
d'- In ordinal ratings,
e'- Which do NOT add up to measures.
Raw Scores are NOT measures
Thorndike was not only aware of the "inequality of the units" counted but also of the non-linearity of any resulting "raw scores". Raw scores are limited to begin at "none right" and to end at "all right". But the linear measures we intend raw scores to imply have no such bounds.
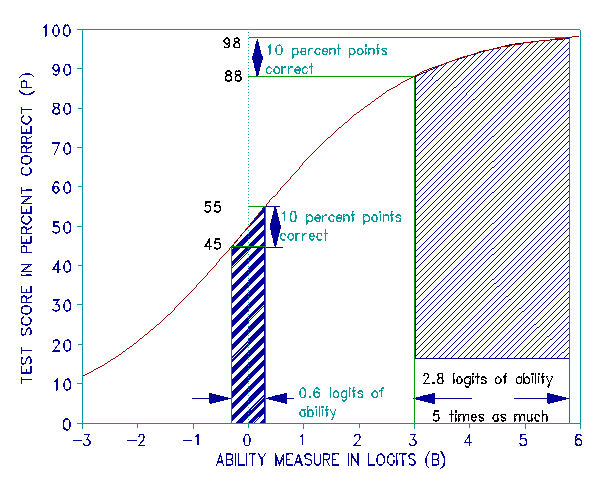
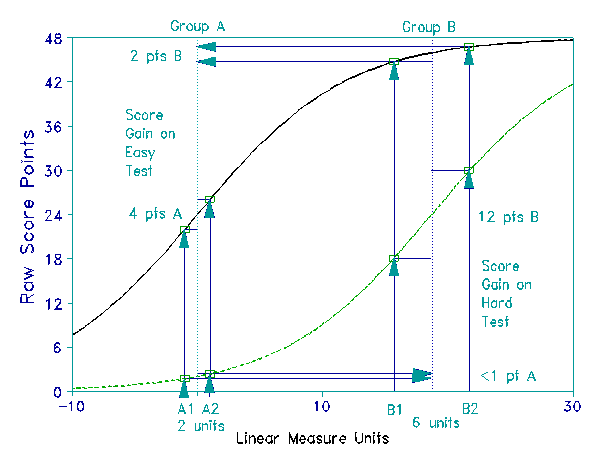
The monotonically increasing ogival exchange between raw scores and measures is illustrated in Figures 1 and 2. The horizontal x-axis in these figures is defined by linear measures. Their vertical y-axes are defined by raw score percents in Figure 1 and by raw score points in Figure 2.

The exchange of one more right answer for a measure increment is steepest where items are dense, usually toward the middle of a test near 50% right. At the extremes of 0% and 100% right, however, the exchange becomes flat. This means that for a symmetrical set of item difficulties one more right answer implies the least measure increment near 50% but an infinite increment at each extreme.
Imagine a situation in which to measure a treatment outcome you inadvertently use a set of questions that are too easy to score on, even before treatment. This unrealized mistargeting will make even the most effective treatment appear ineffective. The same will happen when the set of questions are too hard to score on. Indeed, the apparent effectiveness of the treatment in raw scores will depend entirely on how your questions are targeted on the sample of patients you happen to examine. The size of the raw score increments produced by measure differences among patients and between treatments is entirely subject to the targeting of your test.
Figure 1 shows a typical raw score plotted against measure curve. This curve describes the non-linear rating form raw score (in percent correct) to linear measure relationship of a functional ability measure. Notice that the horizontal measure distance between vertical scores of 88% and 98% is five times greater than the distance between scores of 45% and 55%, even though the raw score differences are an equivalent 10%.
Were we to evaluate the relative effectiveness of alternative treatments A and B in terms of their raw scores, with A centered at a measure of 0 logits and B centered at 4.4 logits on the x-axis, we would be mislead into concluding that the two treatments were equally effective, even though the measures their scores imply show that treatment B is, in fact, five times more effective than treatment A.
Is there any way we can confirm that the raw score bias ratio implied in Figure 1 is really five? To see that "five" is about right, imagine applying a new set of questions which measure along the same variable but are more difficult to score on. Imagine the curve of this harder test to be similar in shape to the curve in Figure 1, but shifted 4.4 logits to the right so that it is centered on the 2.8 logit measure change of treatment B. Now, when we use the new curve to look up the y-axis percent right intercepts for x-axis measures at 3 and 5.8 logits, we see that they imply a raw score increase from 25% to 75% correct instead of 45% to 55%. This is a change of 50% which is indeed five times greater than the previous change of 10%.
Thus, when we compare raw score changes by reexamining each change with a test centered on the region of that change, then we get raw score ratios which resemble the measure ratios made explicit in Figure 1 for any change anywhere along any test. This shows how the linear measures, which can be constructed from raw scores, correct the raw score bias against off target changes and so protect us from being misled by the unavoidable vagaries of mistargeting.
Figure 2, which shows two test curves spaced about 20 linear units apart, illustrates a situation where the apparent advantage of a treatment effect on Group A from A1 to A2 of 4 raw score points over a treatment effect on Group B from B1 to B2 of only 2 raw score points is, in fact, reversed when these same raw scores are converted to equated linear measures. Now the advantage is with the six linear unit change of Group B over the merely two linear unit change of Group A.
This interpretation is confirmed when we examine the second dashed test curve centered at 20 linear units to the right of the solid test curve centered at zero. Now on this "harder" test we see that the targeted raw score increment for Group B at 12 points is three times the targeted raw score increment for Group A of only 4 points.
This example shows that when we rely on raw scores alone to judge the relative magnitude of outcome changes taking place at different distances from the center of the test curve we happen to be working with, we can come to conclusions so mistaken that they reverse our findings. We can conclude the opposite of what our data, when converted from ordinal raw scores to linear measures, make plain.
Table 1 documents the magnitude of raw score bias against extreme measures for a test of normally distributed item difficulties and a test of uniformly distributed item difficulties. The table uses ratios to compare the measure increments corresponding to one more rating step up at the next to largest extreme step with the measure increments corresponding to one more step up at the smallest central step.
| Number of Steps* |
Normal Test |
Uniform Test |
| 10 | 2.0 | 3.5 |
| 25 | 4.6 | 4.5 |
| 50 | 8.9 | 6.0 |
| 100 | 17.6 | 8.0 |
|
* e.g. A 7 category rating scale
supplies 6 steps per item. 13 such
items produce 6 x 13 = 78 steps. These calculations are explained on pages 143-151 of Best Test Design (Wright & Stone 1979). The ratio for a normal test of L items is: loge{2(L-1)/(L-2)}/loge{(L+2)/(L-2)} | ||
We can see in Table 1 that even when items are spread in uniform increments of item difficulty, the raw score bias against measure increments at the extremes can easily be a factor of 5 or more. When items cluster in the middle of a test, the usual case, then the bias can reach a factor of 10 or more. Should we happen to research a comparison of outcome treatments, where the treatment effects are centered at different levels of functional independence, the less effective treatment could easily appear five times better than the more effective treatment simply because these treatment effects were targeted differently by the test we happened to use.
Raw score bias is not limited to dichotomous responses. Because of the effect of additional within item steps, the bias is even more severe for partial credits, rating scales and, of course, the infamous Likert Scale, the misuse of which pushed Thurstone's seminal 1920's work on how to transform raw scores into linear measures out of use.
These examples of raw score bias in favor of central scores and against extreme scores, show that raw scores are target biased and sample dependent (Wright & Stone 1979, Wright & Masters 1982, Wright & Linacre 1989). Any statistical method like linear regression, analysis of variance, generalizability, LISREL or factor analysis that misuses non-linear raw scores or Likert scales as though they were linear measures will have its output systematically distorted by this bias. Like the raw scores on which they are based, all results will be target biased and sample dependent and hence inferentially ambiguous. Little wonder that so much so-called social science is nothing more than transient description of never to be reencountered situations easy to contradict with almost any replication. The obvious and easy to practice (Wright & Linacre 1997, Linacre & Wright 1997) law of measurement is that:
Before applying linear statistical methods to concrete raw data, one must first use a measurement model to construct, from the observed raw data, abstract sample and test free linear measures.
There are also two additional advantages obtained by model-controlled linearization which are decisive for successful scientific research. Each measurement-model-estimated measure and calibration are now accompanied by realistic estimates of precision and mean square residual-from-expectation evaluations of the extent to which their data patterns fit the measurement model, i.e. their statistical validity. When we then proceed to plotting results and applying linear statistics to study relationships among measures, we not only have linear measures to work with but also know their precision and validity.
Table 2 summarizes the important differences between concrete ordinal raw scores and abstract interval linear measures.
Additivity is the first difference. Without additivity one cannot use ordinary arithmetic to analyze ones results. One cannot apply the usual linear statistics of analysis of variance or regression without incurring the irresolvable ambiguities caused by raw score bias against off-target measures.
Continuity is a second difference. Raw scores are forced to vary discontinuously in the integer steps which correspond to one more and one less observation. Fractions are unobservable. Measures, on the other hand, being abstract representations of theoretical constructs are continuous in our imagination and so too in our mathematical analyses. In practice, of course, the values we can estimate for our measures are only as fine-grained as we can build measuring devices to approximate them. But that makes the discontinuity entirely a question of instrumentation engineering. Our ideas of our measures remain continuous.
Status refers to the implacable reality that raw scores are limited to being nothing more than finite examples of what we are looking for and hence forever incomplete. Measures, on the other hand, are, in our stochastic conception of them, complete ideas.
Control refers to the opportunity when working with measures estimated from raw scores to compare the observation values expected from the measures by our measurement model with the observations actually obtained. These enables a continuous, on-line supervision of the empirical validity of our theoretical measures.
Generality follows from interpreting our raw data as an example of an enduring stochastic process which is closely governed by conjointly estimable measurement parameters. This is what enables us to take the inferential step from a finite concrete situation-bound experience to an infinitely reproducible abstract situation-liberated idea.
| FEATURE | CONCRETE ORDINAL RAW SCORES | ABSTRACT LINEAR MEASURES |
| ADDITIVITY: | non-additive | additive |
| non-linear | linear | |
| bent | straight | |
| CONTINUITY: | discrete | continuous |
| lumpy | smooth | |
| STATUS: | incomplete | complete |
| raw | refined | |
| CONTROL: | unsupervised | supervised |
| unvalidated | validated | |
| wild | tamed | |
| GENERALITY: | local | general |
| concrete | abstract | |
| irreproducible | reproducible | |
| test-bound | test-free |
The general ideas summarized in Table 2 draw us into the scientific history of fundamental measurement.
Concatenation
In 1920 English physicist Norman Campbell deduced that the "fundamental" measurement (on which the success of physics was based) required, at least by analogy, the possibility of a physical concatenation, like joining the ends of sticks to concatenate length or piling bricks to concatenate weight.
Sufficiency
In 1920 English mathematician Ronald Fisher, while developing his "likelihood" version of inverse probability to construct maximum likelihood estimation, discovered a statistic so "sufficient" that it exhausted all information concerning its modeled parameter from the data in hand. Statistics which exhaust all modelled information enable conditional formulations by which a value for each parameter can be estimated independently of all other parameters in the model. This necessity for the construction of fundamental measurement follows because the presence of a parameter in the model can be replaced by its sufficient statistic. Fisher's sufficiency enables independent parameter estimation for models that incorporate many different parameters (Andersen 1977). This leads to a second law of measurement:
When a measurement model employs parameters for which there are no sufficient statistics, that model cannot construct useful measurement because it cannot estimate its parameters independently of one another.
Divisibility
In 1924 French mathematician Paul Levy (1937) proved that the construction of an inferentially stable law required infinitely divisible parameters. Levy's divisibility is logarithmically equivalent to the conjoint additivity (Luce & Tukey 1964) which we now recognize as the mathematical generalization of the concatenation Campbell required for fundamental measurement. Levy's conclusions were reenforced in 1932 when Russian mathematician A.N.Kolmogorov (1950 pp.9 & 57) proved that independence of parameter estimates also required divisibility, this time in the form of an additive decomposition.
Thurstone
Between 1925 and 1932 American electrical engineer Louis Thurstone published 24 articles and a book on the construction of psychological measures and developed mathematical methods which came close to satisfying every measurement requirement of which Thurstone was aware.
Unidimensionality:
The measurement of any object or entity describes only one attribute of the object measured. This is a universal characteristic of all measurement. (Thurstone 1931, p.257)
Linearity:
The very idea of measurement implies a linear continuum of some sort such as length, price, volume, weight, age. When the idea of measurement is applied to scholastic achievement, for example, it is necessary to force the qualitative variations into a scholastic linear scale of some kind. (Thurstone & Chave 1929, p.11)
Abstraction:
The linear continuum which is implied in all measurement is always an abstraction...There is a popular fallacy that a unit of measurement is a thing - such as a piece of yardstick. This is not so. A unit of measurement is always a process of some kind which can be repeated without modification in the different parts of the measurement continuum. (Thurstone 1931, p.257)
Sample free calibration:
The scale must transcend the group measured. One crucial test must be applied to our method of measuring attitudes before it can be accepted as valid. A measuring instrument must not be seriously affected in its measuring function by the object of measurement...Within the range of objects...intended, its function must be independent of the object of measurement. (Thurstone 1928, p.547)
Test free measurement:
It should be possible to omit several test questions at different levels of the scale without affecting the individual score (measure)... It should not be required to submit every subject to the whole range of the scale. The starting point and the terminal point...should not directly affect the individual score (measure). (Thurstone 1926, p.446)
Case V of Thurstone's Law of Comparative Judgement (Thurstone 1927) is a fundamental measurement solution for the analysis of paired comparisons.
Guttman
In 1944 American sociologist Louis Guttman pointed out that the meaning of any raw score, including Likert scales, would remain ambiguous unless the score specified every response in the pattern on which it was based.
If a person endorses a more extreme statement, he should endorse all less extreme statements if the statements are to considered a scale...We shall call a set of items of common content a scale if [and only if] a person with a higher rank than another person is just as high or higher on every item than the other person. (Guttman 1950, p.62)
According to Guttman only data which manifest this kind of perfect conjoint transitivity can produce unambiguous measures. Notice the similarity in motivation between Guttman's "scalability" and Ronald Fisher's "sufficiency". Both require that an unambiguous statistic must exhaust the information to which it is said to refer.
Rasch
In 1953 Danish mathematician Georg Rasch (1960) found that the only way he could compare past performances on different tests of oral reading was to apply the exponential additivity of Poisson's 1837 distribution (Stigler 1986, pp.182-183) to data produced by a new sample of students responding simultaneously to both tests. Rasch used Poisson because it was the only distribution he could think of that enabled the equation of the two tests to be entirely independent of the obviously arbitrary distribution of the reading abilities of the new sample.
As Rasch worked out his mathematical solution to what became an unexpectedly successful test equating, he discovered that the mathematics of the probability process, the measurement model, must be restricted to formulations which produced sufficient statistics. Only when his parameters had sufficient statistics could he use these statistics to remove the unwanted person parameters from his estimation equations and so obtain estimates of his test parameters which were independent of the values or distributions of whatever other parameters were at work in the measurement model.
Rasch's description of the conjoint transitivity he requires of the probabilities defined by his measurement model reveal that he has constructed a stochastic solution to the otherwise impossible problem of living up to Guttman's deterministic requirement for the existence of a useful rating scale.
A person having a greater ability than another should have the greater probability of solving any item of the type in question, and similarly, one item being more difficult than another one means that for any person the probability of solving the second item correctly is the greater one. (Rasch 1960, p.117)
Rasch completes his measurement model on pages 117-122 of his 1960 book. His "measuring function" on page 118 specifies the multiplicative definition of fundamental measurement for dichotomous observations as:
Where P is the probability of a correct solution. f(P) is a function of P, still to be determined. b is a ratio measure of person ability. And d is a ratio calibration of item difficulty.
Rasch explains this model as an inverse probability.
The model deals with the probability of a correct solution, which may be taken as the imagined outcome of an indefinitely long series of trials...The formula says that in order that the concepts b and d could be at all considered meaningful, f(P), as derived in some way from P, should equal the ratio between b and d. (Rasch 1960, p .118)
And, after pointing out that a normal probit, even with its second parameter set to one, will be too "complicated" to serve as the measuring function f(P), asks: "Does there exist such a function, f(P), that f(P) = b/d is fulfilled? (Rasch 1960, p .119)
Because "an additive system...is simpler than the original...multiplicative system." Rasch takes logarithms:
loge{f(P)} = loge b - loge d = B - D
which "for technical advantage" he expresses as the logit
L = loge{P/(1-P)}
The question has now reached its final shape: Does there exist a function g(L) of the variable L which forms an additive system in parameters for person B and parameters for items -D such that (Rasch 1960, pp.119-120)
g(L) = B - D
Asking "whether the measuring function for a test, if it exists at all, is uniquely determined" Rasch proves that
f(P) = C{f0(P)}A
"is a measuring function for any positive values of C and A, if f0(P) is so", which "contains all the possible measuring functions which can be constructed from f0(P). So that "By suitable choice of dimensions and units, i.e. of A and C for f(P), it is possible to make the b's and d's vary within any positive interval which may for some reason be deemed convenient." (Rasch 1960, p .121)
Because of "the validity of a separability theorem (sufficiency):
It is possible to arrange the observational situation in such a way that from the responses of a number of persons to the set of items in question we may derive two sets of quantities, the distributions of which depend only on the item parameters, and only on the personal parameters, respectively. Furthermore the conditional distribution of the whole set of data for given values of the two sets of quantities does not depend on any of the parameters." (Rasch 1960, p.122)
With respect to separability, the choice of this model has been lucky. Had we for instance assumed the "Normal-Ogive Model" with all si = 1, which numerically may be hard to distinguish from the logistic - then the separability theorem would have broken down. And the same would, in fact, happen for any other conformity model which is not equivalent in the sense of f(P) = C{f0(P)}A to f(P) = b/d...as regards separability. The possible distributions are limited to rather simple types but lead to rather far reaching generalizations of the Poisson process. (Rasch 1960, p .122)
By 1960 Rasch had proven that formulations in the compound Poisson family, such as Bernoulli's binomial, were both sufficient and, more surprising, necessary for the construction of stable measurement. Rasch had found that the "multiplicative Poisson" was the only mathematical solution to the second step in inference, the formulation of an objective, sample and test free measurement model.
The implications of Rasch's discovery have taken many years to reach practice (Wright 1968, 1977, 1984, Masters & Wright 1984). Even today there are social scientists who do not understand or benefit from what Campbell, Levy, Kolmogorov, Fisher and Rasch have proven (Wright 1992).
Conjoint Additivity
The Americans working on mathematical foundations for measurement were unaware of Rasch's accomplishments. Their work came to a head with the proof by mathematical psychologists Duncan Luce and John Tukey (1964) that Campbell's concatenation was a physical realization of a general mathematical rule which, in its formulation, is "the" definition of fundamental measurement. They called their formulation, which is necessary and sufficient for useful measurement, "conjoint additivity".
The essential character of...the fundamental measurement of extensive quantities is described by an axiomatization for the comparison of effects of arbitrary combinations of "quantities" of a single specified kind...Measurement on a ratio scale follows from such axioms.
The essential character of simultaneous conjointmeasurement is described by an axiomatization for the comparison of effects of pairs formed from two specified kinds of "quantities"... Measurement on interval scales which have a common unit follows from these axioms.
A close relation exists between conjoint measurement and the establishment of response measures in a two-way table ...for which the "effects of columns" and the "effects of rows" are additive. Indeed the discovery of such measures...may be viewed as the discovery, via conjoint measurement, of fundamental measures of the row and column variables. (Luce & Tukey 1964, p.1)
In spite of the practical advantages of such response measures, objections have been raised to their quest...The axioms of simultaneous conjoint measurement overcome these objections...Additivity is just as axiomatizable as concatenation...in terms of axioms that lead to ... interval and ratio scales.
In... the behavioral and biological sciences, where factors producing orderable effects and responses deserve more useful and more fundamental measurement, the moral seems clear: when no natural concatenation operation exists, one should try to discover a way to measure factors and responses such the "effects" of different factors are additive. (Luce & Tukey 1964, p.4)
Although, Luce and Tukey seem to have been unaware of Rasch's work, others (Brogden 1977, Perline, Wright, Wainer 1979) noted that:
The Rasch model is a special case of additive conjoint measurement... a fit of the Rasch model implies that the cancellation axiom (i.e. conjoint transitivity) will be satisfied...It then follows that items and persons are measured on an interval scale with a common unit. (Brogden 1977, p.633)
Our data comes to us in the form of nominal response categories like: yes/no, present/absent, always/usually/sometimes/never, right/wrong, strongly agree/agree/disagree/strongly disagree. The labels we choose for these categories suggest an ordering from less to more, more yes, more presence, more occurrence, more rightness, more agreement. Without thinking much about it, we take for granted that this kind of labeling necessarily establishes a reliable hierarchy of ordinal response categories, an ordered rating scale. Whether empirical responses to such labels are, in fact, actually distinct or even in their expected order, however, remains to be discovered when the data are subsequently studied with an articulate measurement model.
It is not only the unavoidable ambiguity of what is counted nor our lack of knowledge as to the functioning distances between the ordered categories that mislead us. The response counts cannot form a linear scale. Not only are they restricted to occur as integers between none and all. Not only are they systematically biased against off target measures. But, because, at best, they are counts, their natural quantitative comparison will be as ratios rather than differences. Means and standard deviations calculated from these ranks are systematically misleading.
There are serious problems in our initial raw data: ambiguity of entity, non-linearity and confusion of source (Is it the smart person or the easy item that produces the "right" answer?). In addition it is not these particular data which interest us. Our needs focus on what these data imply about future data which, in the service of inference, are by definition "missing". We take the inverse probability step to inference by addressing each piece of observed data, xni, as a stochastic consequence of its modeled probability of occurring, Pnix.
We take the mathematical step to inference by connecting Pnix to a function which specifies how the measurement parameters in which we are interested might govern Pnix. Our parameters could be Bn the location measure of person n on the continuum of reference, Di the location calibration of item i on the same continuum and Fx the threshold of the transition from category (x-1) to category (x).
The necessary and sufficient formulations then are:
in which the symbol "==" means "by definition" rather than merely "equals".
The first formulation shows how this model meets the Levy/Kolmogorov divisibility requirement. The second formulation shows how, in loge odds form, this model meets the Campbell/Luce/Tukey conjoint additivity requirement. On the left we see the replacement of xni by its Bernoulli/Bayes/Laplace stochastic proxy Pnix.
On the right of the second formulation we see the conjoint additivity which produces parameter estimates in the linear form to which our eyes, hands and feet are so naturally accustomed.
Do not forget that when we want to see what we mean, we draw a picture because only seeing is believing. But the only pictures we see successfully are graphs of linear measures. Graphs of ratios mislead us. Try as we might, our eyes cannot "see" things that way. Needless to say, what we cannot see we cannot understand, let alone believe.
Indeed, Fechner (1860) showed that when we experience any kind of ratio -light, sound or pain, - our nervous system "takes its logarithm" so that we can "see how it feels" on a linear scale. Nor was Fechner the first to notice this neurological phenomena. When tuned according to the Pythagorean scale musical instruments sounded out of tune at each change of key. Pythagorean tuning was key-dependent. This inconvenience was resolved in the 17th century, 200 years before Fechner's work, by tuning instruments to notes which increased in frequency by equal ratios.
Equal ratio tuning produces an "equally tempered" scale of notes which sound equally spaced in any key and so are sufficiently "objective" to be "key-free", as it were. Bach's motive for writing "The Well-Tempered Clavier" was to demonstrate the value of this invention.
Inverse Probability in Practice
The use of inverse probability to implement inference
redirects our attention away from seeking models to fit data toward finding data that fit the particular models by which we define measurement. Binomial transition odds like Pnijkx / Pnijkx-1 propel inferential meaning. Our raw data are recorded in terms of categories like right/wrong and agree/disagree. We label these categories: X = 0,1,2,3,4,,, so that each X label counts a step up along the intended order of categories like:
| WRONG X = 0 |
RIGHT X = 1 |
| STRONGLY DISAGREE X = 0 |
DISAGREE X = 1 |
AGREE X = 2 |
STRONGLY AGREE X = 3 |
We then connect X to the circumstances in which we are trying to measure by subscribing X, as in Xnijk, so that Xnijk can stand for a rating earned by performer n on item i from judge j for task k.
Then Pnijkx can be the inverse probability that performer n gets rated X on item i by judge j for task k.
The transition odds that the rating is X rather than X - 1 become Pnijkx/Pnijkx-1, as in:
| Pnijkx-1 | Pnijkx | ||
| X - 2 | X - 1 | X | X + 1 |
We then "explain" the logarithm of these transition odds as the consequence of a conjointly additive parameter composition like Bn-Di-Cj-Ak-Fx so that our measurement model becomes:
This conjoint additivity provides inferential stability.
Three Essential Statistics and their Representation
To use measures wisely we need to know three things about every measure, its:
1. Location on the linear measurement scale, AMOUNT.
2. Range of reasonable values, PRECISION.
3. Empirical coherence, VALIDITY.
Finally, to "see" what our statistics mean, we need to:
4. Plot them into an informative PICTURE.
To estimate the AMOUNT of the measure is, of course, our motivation for constructing it in the first place. But we must realize that no measure, however, carefully constructed, can be exact. There is always some error in the measure. We need to know how big this error is so that we can keep in mind the PRECISION of the measure as we work with it.
There are two main sources of measurement error. The first is an intrinsic component of the stochasticity of our measurement model. The binomial basis for the inverse probability dictates an entirely expected level of measure error. The magnitude of this error component is governed, first by the number of replications, as in, the number of observable steps or the number of rating forms completed and second by the targeting of items on persons.
But that modeled and hence expected error is not all. We can only obtain the data for our measures in a real situation which is inevitably fraught with potentially interfering circumstances. We cannot know ahead of time how much these circumstances muddy our measures. Things are bound to be slightly different every time. Fortunately, the fit statistics of our measurement model give us an excellent indication of how much unplanned for disturbance we actually encounter at each application.
Thus a second error component, determined by the situation in which our raw data are obtained, which always decreases the actual precision of our measures must be factored into the mathematically modeled precision to produce a precision estimate which is realistic.
Finally, the same fit statistics which help us bring our measure precision into rapport with the actual situation in which the raw data were obtained also indicate the general validity of the measure. When the pattern of observed data comes close to the expected values predicted by the measurement model, then we can see that our measure and its error are valid. But, when some of the observed values wander far from expectation, then we cannot overlook the fact that something has interfered with the data collection for our measure and so made our measure less valid than we might have wished.
A useful feature of the comparisons between observed and expected raw responses is that the specificities of these discrepancies, which person, which item, often show us what caused the interference and so suggest how we might control the intrusion of further interferences of this kind.
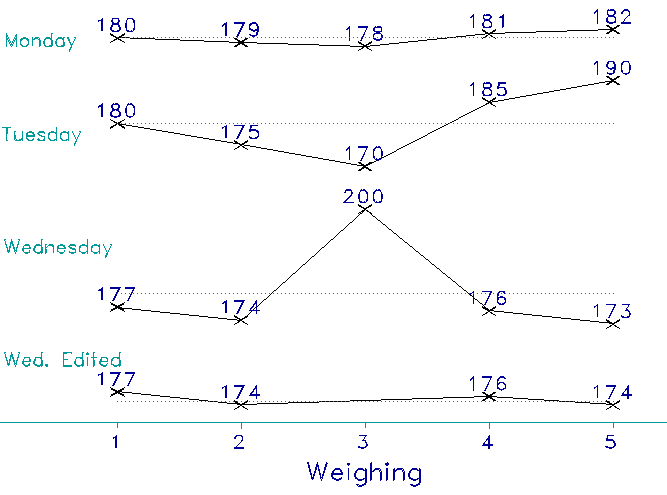
To illustrate with a homely example, imagine that, in order to evaluate my "miracle" diet, I weigh myself five times each morning and record the following readings from my bathroom scale:
On Monday I read, in pounds: 180 - 179 - 178 - 181 - 182.
Mean = 180, Error = ±1, Range = 178-182
The five readings cluster nicely. It is obvious that 180 is a rather precise estimate of my Monday weight - to the nearest pound.
On Tuesday, however, the weights I read are different:
180 - 175 - 170 - 185 -190.
Mean = 180, Error = ± 5, Range = 170-190
Results which are still valid but somewhat imprecise.
The way I used my scale on Tuesday was obviously not as accurate as on Monday. Am I jumping on the scale too roughly? My best Tuesday estimate of my weight is still 180, but now only to the nearest 5 pounds, perhaps too crude to detect any success from my diet.
So on Wednesday I am careful how I step on the scale, but, alas, something else goes wrong:
177 - 174 - 200 - 176 -173
Mean = 180, Error = ???, Range = 173-200
These results must be invalid!
One of my five weighings does not make sense. How could I suddenly weigh 20 pounds more? Was that the moment my wife, trying to see how much I weighed, leaned on my shoulder as I stood on the scale? One thing for sure, that reading of 200 is out of line with the other four readings and has to be reconsidered.
Now, look at how nice and sensible my results become when I omit that wild 200:
177 - 174 - 176 -173
Mean = 175, Error = ±1, Range = 173-177
Once again both valid and precise. And, glory be, I'm 5 pounds lighter! My diet is working!
We discovered the measurement hazards in my weighing story by reading my numbers carefully. But reading numbers takes concentration. Few of us do it well. I'll bet that, had I not dramatized that errant "200", you might have missed it and come to the wrong conclusion about the success of my diet. To avoid the easy mistake of misreading tables of numbers, it is always a good idea to make a picture of the numbers in some kind of plot. Plots of numbers are always better than tables.
Let's see what my weighings look like when I plot them. Figure 3 tells my weighing story at a glance. No need to read anything carefully. The increase of uncertainty from Monday to Tuesday is obvious and the irregularity of that "200" on Wednesday is glaring. You cannot miss either of them. You can also see, directly, that once the "200" is excluded from Wednesday's readings, Wednesday's precision is as good as Monday's and that I have definitely lost some weight.
Why did I weigh myself five times each morning? By now you should be able to answer that question quite easily. What if I had weighed myself only once and that one reading turned out to be the 200? How misled I would have been. Ask yourself the same question in a more dramatic context. How many tosses of my Lucky Quarter would you demand to check for fairness before you bet your life on it? Would once or twice be enough? Not likely!
What does that mean about scores and measures? One observation, one score from one item, is never enough! Neither is one mere second opinion enough! To make a wise or even sensible decision we must obtain several independent replications of the relevant measures before we act!
The moral of this story is that:
We need MEASURES not scores, else change is without evidence.
We need to know the PRECISION of our measures, else their implications remain obscure.
We need to verify the VALIDITY of our measurement process by obtaining several independent replications, else meaning is uncertain.
No matter how smart we are, we need more than one observation, more than one opinion. We need REPLICATIONS.
Finally, a plot is worth a thousand numbers. Indeed a good PICTURE may be the only way to "see" what a set of numbers mean.
To do this kind of analysis with your data, you record your category ratings on disk and analyze them with a computer program like BIGSTEPS or FACETS. (Wright & Linacre 1997, Linacre & Wright 1997) This kind of analysis will give you tables, maps, keys and files of conjoint linear measures.
The following example of Rasch BIGSTEPS analysis comes from 3128 administrations of the 8 item PECS© Applied Self-Care LifeScale. This scale evaluates eight aspects of self-care:
BOWEL Program
URINARY Program
SKIN CARE Program
Health COGNIZANCE
Health ACTIVITY
Health EDUCATION
SAFETY Awareness
MEDICATION Knowledge
by asking a nurse to rate the patient's competence on each of the eight items according to a seven category rating scale intended to bring out gradients of competence for each item, like these categories for the Bowel Program item:
BOWEL Program effectiveness concerns regulation of bowel elimination. Prevention of complications includes: regulation of food and fluids; high fiber diet; medications for stimulation or prevention of diarrhea; digital stimulation; and colostomy care.
RATING CATEGORY DEFINITION
1 INEFFECTIVE:Less than 25% effective.
2 DEPENDENT:25% - 49% effective.
3 DEPENDENT:50% - 74% effective.
4 DEPENDENT:75% - 100% effective.
5 INDEPENDENT:50% - 74% effective.
6 INDEPENDENT:75% - 100% effective.
7 NORMAL:Self maintenance.
The data matrix has 3128 rows, a row for each patient n, and 8 columns, a column for each item i. The cell entry xni is an ordinal rating from 1 to 7 of patient n on item i. BIGSTEPS analyzes this matrix of 25,024 raw data points to produce the best possible:
1. 8 item calibrations to define the PECS© Applied Self-Care construct,
2. for each item, 6 rating step calibrations to its step structure and
3. 3,128 measures of the extent of each patient's self-care.
The analysis not only extracts the best possible linear measurement framework, but also reduces the complexity of the data from 25,024 raw ordinal data points to a mere 8 item calibrations + 48 item step calibrations + 3,128 person measures, all 3,184 of which estimates are expressed in linear metrics on a common scale which measures a single dimension of "self-care"!
ENTERED: 3128 PATIENTS ANALYZED: 2145 PATIENTS 8 ITEMS 56 CATEGORIES
SUMMARY OF 2145 MEASURED (NON-EXTREME) PATIENTS
RAW MODEL INFIT OUTFIT
SCORE COUNT MEASURE ERROR MNSQ MNSQ
MEAN 26.2 7.5 41.56 4.94 .88 .89
S.D. 11.0 .9 22.09 1.35 1.06 1.10
MODEL RMSE 5.12 ADJ.SD 21.49 SEPARATION 4.19 RELIABILITY .95
REAL RMSE 5.80 ADJ.SD 21.32 SEPARATION 3.68 RELIABILITY .93
S.E. OF PERSON MEAN .48
MAXIMUM EXTREME SCORE: 5 PATIENTS MINIMUM EXTREME SCORE: 94 PATIENTS
LACKING RESPONSES: 884 PATIENTS VALID RESPONSES: 94.3%
SUMMARY OF 8 MEASURED (NON-EXTREME) ITEMS
RAW MODEL INFIT OUTFIT
SCORE COUNT MEASURE ERROR MNSQ MNSQ
MEAN 7034.1 2023.1 50.01 .28 .83 .88
S.D. 829.2 148.5 4.83 .02 .23 .24
MODEL RMSE .29 ADJ.SD 4.82 SEPARATION 16.91 RELIABILITY 1.00
REAL RMSE .29 ADJ.SD 4.82 SEPARATION 16.64 RELIABILITY 1.00
S.E. OF ITEM MEAN 1.82
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
What follows are excerpts from Richard Smith's BIGSTEPS analysis of these data. It is unreasonable for you to expect yourself to master every detail shown in these excerpts. Instead, I urge you to sit back and notice, to whatever extent is comfortable for you, the various ways this kind analysis can bring your inevitably complicated data into a few well-organized tables and pictures.
Table 3 summarizes the results of an 87% reduction of the raw ordinal data and describes the summary characteristics of its reconstruction into a unidimensional measurement framework. Table 3 contains more information than we can discuss here, but there are two points to note:
1. 2145 patients are measured at non-extreme scores and among these the data completion is 94.3%.
2. The reliability of this 8 item scale to separate the self-care measures of these 2145 patients is a high .93.
MEASURE PATIENTS RATING.APPLIED SELF-CARE
90 . 6.KNOWS MEDICATIONS
.
.# Q 6.HEALTH ACTIVITY
. 6.SAFETY AWARENESS
80 .## 6.SKIN CARE PROGRAM
.### 6.BOWEL PROGRAM
.## 6.URINARY PROGRAM
.#####
70 .###
.#####
#########
######### S
60 .######## 4.KNOWS MEDICATIONS
.##########
.#### 4.HEALTH ACTIVITY
.########## 4.SAFETY AWARENESS
50 .##### 4.SKIN CARE PROGRAM
.####### 4.BOWEL PROGRAM
##### 4.URINARY PROGRAM
######## M
40 .############ 3.KNOWS MEDICATIONS
.###########
.######### 3.HEALTH ACTIVITY
.###### 3.SAFETY AWARENESS
30 .###### 3.SKIN CARE PROGRAM
.####### 3.BOWEL PROGRAM
.####### 3.URINARY PROGRAM
.######
20 .##### S
.######
.#####
.#### 1.KNOWS MEDICATIONS
10 .####
.# 1.HEALTH ACTIVITY
. 1.SAFETY AWARENESS
.## 1.SKIN CARE PROGRAM
0 .# 1.BOWEL PROGRAM
.### Q 1.URINARY PROGRAM
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
To see the meaning of the BIGSTEPS definition of the PECS© Self-Care construct, we plot the item calibrations and patient measures together on the MAP in Figure 4. The left column benchmarks the linear units of the measurement framework, scale for this analysis to run from -20 to 120. The MAP is focused on the region from 0 to 90.
The second column shows the frequency distribution of the patients who measure between 0 and 90. The symbols M, S and Q mark the mean patient measure at M, plus and minus one standard deviation at each S and plus and minus two standard deviations at each Q. Finally, on the right, six of the eight items defining this self-care construct are shown in their calibration order four times, once at each of the rating levels 1 at "Ineffective", 3 and 4 at "Dependent" and 6 at "Independent".
This was done so that you could see how this definition of self-care moves up from ratings of ineffectiveness in the 0 to 10 measure region, through two successive levels of dependence in the 25 to 60 measure region to ratings of independence in the 75 to 90 measure region.
Figure 4 shows only six of the eight items because the two other items, MEDICATIONS and EDUCATION calibrate on top of each other at the same high level has do SKIN CARE and COGNIZANCE a bit lower down.
The mapped hierarchy of the 6 items begins with the URINARY and BOWEL programs which are the easiest to rate well on and moves up through SKIN CARE (and COGNIZANCE), SAFETY and ACTIVITY to reach MEDICATIONS (and EDUCATION) which are the hardest self-care programs to rate well on.
The practical application of this empirical hierarchy is that self-care education has the best chance of success when it begins at the easy end with URINARY and BOWEL programs and only reaches up to the more challenging ACTIVITY and MEDICATIONS programs after the easier programs are well established.
ITEMS STATISTICS: MEASURE ORDER
ENTRY RAW INFIT OUTFIT
NUM SCORE COUNT MEASURE ERROR MNSQ MNSQ PTBIS HARDEST ITEM
8 5964 1866 57.4 .3 .96 .97 .82 KNOWS MEDICATIONS
6 5828 1832 57.1 .3 .66 .68 .89 HEALTH EDUCATION
5 6294 1800 52.1 .3 .72 .74 .87 HEALTH ACTIVITY
7 7458 2137 48.9 .3 .71 .78 .86 SAFETY AWARENESS
4 7413 2135 48.2 .3 .47 .49 .91 HEALTH COGNIZANCE
3 7290 2139 48.1 .31.22 1.29 .77 SKIN CARE PROGRAM
1 7858 2141 44.6 .3 .82 .92 .83 BOWEL PROGRAM
2 8168 2135 43.7 .31.09 1.16 .80 URINARY PROGRAM
MEAN 7034. 2023. 50.0 .3 .83 .88 EASIEST ITEM
S.D. 829. 148. 4.8 .0 .23 .24
INPUT: 3128 PATIENTS, 8 ITEMS
ANALYZED: 2145 PATIENTS, 8 ITEMS 56 CATEGORIES
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
Table 4 lists the item calibrations from which the right side of Figure 4 was mapped. This table shows all 8 items in their difficulty order and lists their calibrations, calibration standard errors and fit statistics by which the validity of these calibrations can be judged. The fit statistics, which have expected values of 1.00 show that the only item afflicted with calibration uncertainty is the SKIN CARE program item with mean square residual ratios of 1.22 and 1.29.
These fit statistics suggest that skin care may sometimes interact idiosyncratically with other patient characteristics like age, sex or impairment. Further examination of other BIGSTEPS output can be used to identify the particular patients who manifest the effects of such an interaction and hence bring out the individual diagnostics which are most helpful to these particular patients.
The analysis of the extent to which any particular set of data cooperates with a measurement model to define a desired variable and estimate useful measures along that variable is decisive in the construction of good measures. We cannot do justice to this important topic here. But an excellent place to look for extensive and articulate explanations and applications is in the published work of Richard Smith. (Smith 1985, 1986, 1988, 1991, 1994, 1996)
Figure 5
Rating Category Step Structure: BOWEL
PECS© LifeScales: Applied Self-Care Construct
BOWEL PROGRAM RATING CATEGORY PROBABILITIES
P
R 1.0 Ineffective Normal
O 111 7777
B 11 77
A 11 77
B .8 1 Independent 7
I 1 7
L 1 7
I 1 Dependent 44 7
T .6 1 44 4 7
Y 1 4 4 7
.5 1 2222 3333 4 4 7
O * 233 * 4 7
F .4 21 32 43 4 7
2 1 3 2 4 3 4 7
R 2 1 3 2 4 3 5*6*666
E 22 * * 3 55 6* 6
S .2 2 31 42 3 5 6 *55 66
P 2 3 1 4 2 5* 6 7 4 5 6
O 222 33 1*4 2 5 3* 7 4 5 666
N 222 33 44 11 *** 667*3 44555 6666
S .0 *********************************************************
E
-25 -5 15 35 55 75 95 115
MEASURE
3 1 1 1 11112222222234222241333431311 1
2 6 4 4 31671212716708664379546145138996 7 1 2 3 6
PATIENT 6 55216473961979258068811527561823331476839 9 9 3 2
Q S M S Q
BOWEL PROGRAM RATING STEP CALIBRATIONS
CATEGORY STEP OBSERVED STEP STEP EXPECTED SCORE MEASURES
LABEL VALUE COUNT MEASURE ERROR STEP-.5 AT STEP STEP+.5
Ineffective 1 618 NONE ( -6 ) 13
2 2 1049 7 .6 13 13 22
Dependent 3 1794 21 .4 22 30 40
4 4 2503 38 .3 40 50 58
Independent 5 860 66 .4 58 63 67
6 6 727 66 .4 67 72 78
Normal 7 1010 70 .5 78 ( 84 )
mode mean
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
Figure 5 illustrates the way BIGSTEPS analyzes how this set of categories are used to obtain patient ratings on each item. The item chosen here is the easiest BOWEL program. The plot in the top half of Figure 5 shows how the probabilities of category use from 1 up to 7 move to the right across the variable from low measures at -25 to high measures at +115. We can see that each rating category in sequence has a modal region of greatest probability except for categories 5 and 6 which can be seen to be underused on this item.
This observation about the usage of categories 5 and 6 could lead us to question their distinction and, perhaps, to consider combining them into one category of "independence".
Below the plot is the frequency distribution of the 8567 patient ratings used for this analysis. At the bottom are observed counts, step difficulty calibrations and measures expected at each rating level from 1 to 7. In the column labeled "OBSERVED COUNT" we see that the uses of categories 5 and 6 at counts of 860 and 727 fall far below the uses of category 4 at a count of 2503. That is why the curves for those two categories do not surface at the top of Figure 5.
PATIENT EDUCATION RATING CATEGORY PROBABILITIES
P
R 1.0
O Ineffective Normal
B 11 7
A 11 7
B .8 1 Independent 77
I 1 7
L 1 Dependent 6666 7
I 1 6 66 7
T .6 1 2222 6 6 7
Y 1 2 2 333 6 6 7
.5 12 2 3 33 6 *
O 21 23 3 55556 7 6
F .4 2 1 32 344445 65 7 6
2 1 3 2 443 54 6 5 7 6
R 2 1 3 2 4 35 4 6 5 7 6
E 2 1 3 24 * * 5 7 6
S .2 2 * 42 5 3 6 4 5 7 66
P 22 3 1 4 2 5 36 4 5* 6
O 22 33 11 4 * 63 4 77 55 6
N 333 4** 55 22*6 333 *** 555
S .0 *********************************************************
E
-13 7 27 47 67 87 107 127
MEASURE
3 1 1 1 11112222222234222241333431311 1
2 6 4 4 31671212716708664379546145138996 7 1 2 3 6
PATIENT 6 55216473961979258068811527561823331476839 9 9 3 2
Q S M S Q
PATIENT EDUCATION RATING STEP CALIBRATIONS
CATEGORY STEP OBSERVED STEP STEP EXPECTED SCORE MEASURES
LABEL VALUE COUNT MEASURE ERROR STEP-.5 AT STEP STEP+.5
Ineffective 1 849 NONE ( -1 ) 18
2 2 1727 11 .5 18 22 33
Dependent 3 2018 33 .4 33 42 50
4 4 1403 50 .4 50 57 64
Independent 5 1233 63 .4 64 70 79
6 6 799 86 .5 79 92 108
Normal 7 92 107 1.2 108 ( 118 )
mode mean
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
Figure 6 gives the same information for the hardest EDUCATION item. We can see that the measure scale under the plot has moved up 12 units and that the step difficulties and expected measures have also increased. In the category curves for this item every category is seen to have its day in the sun. We would not be tempted to combine any of these categories.
|
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
Maps and summaries of item and category performance are essential to our analysis of the measurement quality of our test. But our ultimate aim, of course, is the measurement and diagnosis of each of our patients. This concern brings us to the diagnostic KEY forms illustrated in Figures 7 and 8.
After the construct MAP of Figure 4, KEY forms are the second most useful outcome of a BIGSTEPS analysis. Figure 7 shows two patients who received the same rating scores of 36 raw score points, but who differ decisively in the best estimates of their self-care measures and who also differ in the diagnostic implications of their particular self-care ratings.
The typical patient at the top of Figure 7 measures at 60 self-care units which puts them at the 70th percentile among a normative group of 8561 patients. This patient is verging on self-care independence except for some additional help with the hardest programs, medication and education.
The atypical patient at the bottom of Figure 7 with the same raw score, however, appears differently when recorded on their own KEY form. When their abysmal ineffectiveness in the medication and education programs is set aside, they measure up at 73 units and the 85th percentile. They are well into independence on everything except education and medication. But, in those two aspects of self-care, they are dramatically deficient. Obviously their self-care education must concentrate on the earliest levels of these two areas.
|
| Output from BIGSTEPS (Wright, B.D. & Linacre, J.M. 1997) |
Figure 8 shows a KEY form for another construct, Cognition and Communication. The patient is also atypical. This time in a particular way which we may have learned implies a particular diagnosis. The deficiencies for this patient, short term memory, attention/concentration and orientation suggest the possibility of Alzheimer's.
Notice how well, when a firm well-labeled frame of reference is constructed, we can then become aware of and attend to idiosyncratic aspects of patient status. The two patients in Figure 7 are not treated the same because they happen to have the same raw scores of 36. On the contrary, when we have a frame of reference we can ask about more than their score. We can ask how they got the score? And, when their pattern of ratings contains values which, because of the structure of our measurement frame of reference, are unexpected, we can identify and respond to the details of their particular personal needs.
Methodological Summary
1. Ratings are chancy. But they are all we can observe. They may contain good information. But it is always in a fuzzy state.
2. Raw scores are not measures. Raw scores are biased against off target performance, are sample dependent, inferentially unstable and non-linear.
3. Inverse probability explained by conjointly additive parameters enables the construction of clear measures from fuzzy raw scores.
4. These measures, in turn, enable MAPs which define the variable completely in a one page, easy to grasp and remember, graphical report on the construct which our analysis has realized as a measurable variable.
5. The measures also enable individual KEYs which apply the variable sensitively and individually to each and every person to bring out their personal particulars in an easy to review, understand and work from one page graphical person report.
A weight of seven was a tenant of faith among seventh century Muslims. Muslim leaders were censured for using less "righteous" standards (Sears, 1997). Caliph of the Muslim world, 'Umar b. 'Abd al-'Aziz, instructs his governor in al-Kufa that:
The people of al-Kufa have been struck with trial, hardship, oppressive governments and wicked practices set upon them by evil tax collectors. The more righteous law is justice and good conduct...I order you to take in taxes only the weight of seven. (Damascus, 723)
The Magna Carta of John, King of England, requires that:
There shall be one measure of wine throughout Our kingdom, and one of ale, and one measure of corn, to wit, the London quarter, and one breadth of cloth,..., to wit, two ells within the selvages. As with measures so shall it be with weights. (Runnymede, 1215)
Thus we see that commerce and politics were the first source of stable units for length, area, volume and weight. The steam engine added temperature and pressure. The subsequent successes of science stand on these commercial and engineering achievements. When we recall the long standing political and moral history of units of taxation and trade we realize that when units are unequal, when they vary from time to time and place to place, it is not only unfair. It is also immoral. So too with the misuse of necessarily unequal and so unfair raw score units, when they are analyzed as though they were fair measures.
The main purpose of measurement is inference. We measure to inform and specify our plans for what to do next. If our measures are unreliable, if our units vary in unknown ways, our plans must go astray. This point might seem small. Indeed, it has been belittled by many, presumably knowledgeable, social scientists as not worth worrying about. But, far from being a small point, it is a decisive one! We will not build a useful, let along moral, social science until we stop deluding ourselves by analyzing raw scores as though they were measures.
The concrete measures which help us make life better are so familiar that we seldom think about "how" or "why" they work. Although the mathematics of measurement did not initiate its practice, it is the mathematics of measurement which provide the ultimate foundation for practice and the final logic by which useful measurement evolves and thrives. A mathematical history of measurement, however, takes us behind concrete practice to the theoretical requirements which make the practical success of measurement possible. There we discover that:
1. Measures are inferences,
2. Obtained by stochastic approximations,
3. Of one dimensional quantities,
4. Counted in abstract units, of sizes which are
5. Intended to undisturbed by extraneous factors.
To meet these requirements mathematically,
Measurement must be an inference of values for infinitely divisible parameters which define the transition odds between observable increments of a theoretical variable.
Table 5 summarizes an anatomy of inference according to four obstacles which stand between raw data and the stable inference of measures they might imply.
| OBSTACLES | SOLUTIONS | INVENTORS |
| UNCERTAINTY have -> want now -> later statistic -> parameter |
PROBABILITY binomial odds regular irregularity misfit detection |
Bernoulli 1713 Bayes 1764 Laplace 1774 Poisson 1837 |
| DISTORTION non-linearity unequal intervals incommensurability |
ADDITIVITY linearity concatenation conjoint additivity |
Fechner 1860 Helmholtz 1887 N.Campbell 1920 Luce/Tukey 1964 |
| CONFUSION interdependence interaction confounding |
SEPARABILITY sufficiency invariance conjoint order |
Rasch 1958 R.A.Fisher 1920 Thurstone 1925 Guttman 1944 |
| AMBIGUITY of entity, interval and aggregation |
DIVISIBILITY independence stability reproducibility exchangeability |
Levy 1924 Kolmogorov 1932 Bookstein 1992 de Finetti 1931 |
| For Bernoulli, Bayes, Laplace, Poisson and Helmholtz see Stigler (1986). |
Uncertainty is the motivation for inference. The future is uncertain by definition. We have only the past by which to foresee. Our solution is to capture uncertainty in a skein of imaginary probability distributions which regularize the irregularities that disrupt connections between what seems certain now but is certainly uncertain later. We call this step "inverse probability".
Distortion interferes with the transition from observation to conceptualization. Our ability to figure things out comes from our faculty to visualize. Our power of visualization evolved from the survival value of body navigation through the two dimensional space in which we live. Our antidote to distortion is to represent our observations of experience in the linear form that makes them look like the space in front of us. To "see" what experience "means", we "map" it.
Confusion is caused by interdependencies. As we look for tomorrow's probabilities in yesterday's lessons, confusing interactions intrude. Our resolution of confusion is to simplify the complexity we experience into a few shrewdly crafted "dimensions". The authority of these dimensions is their utility. Final "Truths" are unknowable. But, when our inventions work, we find them "useful". And when they continue to work, we come to believe in them and to call them "real" and "true".
The method we use to control confusion is to enforce unidimensionality. We define and measure one invented dimension at a time. The necessary mathematics is parameter separability. Models which introduce putative "causes" as separately estimable parameters are our laws of quantification. These models define measurement, determine what is measurable, decide which data are useful and expose data which are not.
Ambiguity, a fourth obstacle to inference, occurs because we can never determine exactly which particular definitions of existential entities are the "right" ones. As a result the only measurement models that can work are models that are indifferent to level of composition. Bookstein (1992, 1996, 1997) shows that to accomplish this the models must embody parameter divisibility or additivity as in:
Fortunately the mathematical solutions to Ambiguity, Confusion and Distortion are identical. The parameters that govern the probabilities of the data must appear in either a divisible or additive form.
Inverse Probability
A critical turning point in the mathematical history of measurement is the application of Jacob Bernoulli's 1713 binomial distribution as an inverse probability for interpreting the implications of observed events (Thomas Bayes, 1764, Pierre Laplace, 1774 in Stigler 1986, pp. 63-67, 99-105). The data in hand are least of what we seek. Our interests go beyond to what these data imply about other data still unmet, but important to foresee. When we read our weight as 180 pounds, we take that number, not as a one-time, local description of a particular stepping on the scale, but as our "weight" for now, just before now, and, inferentially, for awhile to come.
The first problem of inference is how to infer values for these other data, which, by the meaning of "inference", are currently "missing". Since the purpose of inference is to estimate what future data might be like before they occur, methods which require complete data cannot be methods of inference. This realization engenders a third law of measurement:
Any statistical method nominated to serve inference which requires complete data, by this requirement, disqualifies itself as an inferential method.
But, if what we want to know is "missing", how can we use the data in hand to make useful inferences about the "missing" data they might imply? Inverse probability reconceives our raw observations as a probable consequence of a relevant stochastic process with a useful formulation. The apparent determinism of formulae like F = MA depends on the prior construction of relatively precise measures of F and A. The first step from raw observation to inference is to identify the stochastic process by which an inverse probability can be defined. Bernoulli's binomial distribution is the simplest and most widely used process. Mathematical analysis proves that the compound Poisson is the parent of all such measuring distributions.
Conjoint Additivity
The second step to inference is to discover what mathematical models can determine the stochastic process in a way that enables a stable, ambiguity resilient estimation of the model's parameters from the data in hand. At first glance, this step looks obscure. Its twentieth century history has followed so many paths, traveled by so many mathematicians and physicists that one might suppose there were no clear second step but only a jumble of unconnected possibilities along with their seemingly separate mathematical resolutions. Fortunately, reflection on the motivations for these paths and examination of their mathematics leads to a reassuring simplification. Although each path was motivated by a particular concern as to what inference must overcome to succeed, all solutions end up with the same simple, easy to understand, easy to use formulation. The mathematical function which governs the inferential stochastic process must specify parameters which are either infinitely divisible or conjointly additive i.e. separable. That's all there is to it!
Some fundamental laws of measurement emerge as we explore the definition and necessities of inference:
Any statistical method nominated to serve inference which turns out to require complete data, by this very requirement, disqualifies itself as an inferential method.
When a model employs parameters for which there are no sufficient statistics, that model cannot construct useful measurement because it cannot estimate its parameters independently.
Before applying linear statistical methods to raw data, one must first use a measurement model to construct, from the observed raw data, coherent sample and test free linear measures.
Practical solutions to Thurstones' five requirements:
1. Measures must be linear, so that arithmetic can be done with them.
2. Item calibrations must not depend on whose responses are used to estimate them - must be sample free.
3. Person measures must not depend on which items they happened to take - must be test free.
4. Missing data must not matter.
5. The method must be easy to apply.
were latent in Campbell's 1920 analysis of concatenation, Fisher's 1920 invention of sufficiency and the functional divisibility of Levy and Kolmogorov. Stable inference theory was realized practically by Rasch's 1953 application of the additive Poisson model to the equation of alternative tests of oral reading.
Rasch's original model has since been extended to address every imaginable kind of raw observation: dichotomies, rating scales, partial credits, binomial and Poisson counts (Masters & Wright 1984) in every reasonable observational situation i.e. ratings faceted to: persons, items, judges and tasks. Today versatile computer programs are available which make thorough applications of Rasch's "measuring functions" so easy, immediate and accessible to every student of outcome measurement that there is no excuse for stopping analysis at a misconstruction of raw scores.
Despite hesitation by some to use a fundamental measurement model to transform raw scores into measures so that subsequent statistical analysis can become fruitful, there have been many successful applications (Fisher & Wright 1994) and convenient software to accomplish these applications is readily available (Wright & Linacre 1997, Linacre & Wright 1997).
Today, it is easy for any reasonably knowledgeable scientist to use these programs to traverse the decisive step from their unavoidably ambiguous concrete raw observations to well-defined abstract linear measures with realistic precision and validity estimates. Today, there is no methodological reason why outcome measurement cannot become as stable, as reproducible and hence as useful as physics.
The mathematical knowledge needed to construct objective, fundamental measures from raw scores has been with us for more than 40 years. Easy to use computer programs which do the number work have been available for 30 years. What could possibly justify continuing to misuse raw scores as though they were measures when we know that they are not?
MESA Memorandum 66, 1997
Benjamin D. Wright
MESA Psychometric Laboratory
Published as Wright B.D. (1997) Fundamental measurement for outcome evaluation. Physical medicine and rehabilitation : State of the Art Reviews. 11(2) : 261-288.
Andersen, E.B. (1977). Sufficient statistics and latent trait models. Psychometrika, (42), 69-81.
Bookstein, A. (1992). Informetric Distributions, Parts I and II. Journal of the American Society for Information Science, 41(5):368-88.
Bookstein, A. (1996). Informetric Distributions. III. Ambiguity and Randomness. Journal of the American Society for Information Science, 48(1): 2-10.
Brogden, H.E. (1977). The Rasch model, the law of comparative judgement and additive conjoint measurement. Psychometrika, (42), 631-634.
Campbell, N.R. (1920). Physics: The elements. London: Cambridge University Press.
de Finetti, B. (1931). Funzione caratteristica di un fenomeno aleatorio. Atti dell R. Academia Nazionale dei Lincei, Serie 6. Memorie, Classe di Scienze Fisiche, Mathematice e Naturale, 4, 251-99. [added 2005, courtesy of George Karabatsos]
Engelhard, G. (1984). Thorndike, Thurstone and Rasch: A comparison of their methods of scaling psychological tests. Applied Psychological Measurement, (8), 21-38.
Engelhard, G. (1991). Thorndike, Thurstone and Rasch: A comparison of their approaches to item-invariant measurement. Journal of Research and Development in Education, (24-2), 45-60.
Engelhard, G. (1994). Historical views of the concept of invariance in measurement theory. In Wilson, M. (Ed), Objective Measurement: Theory into Practice. Norwood, N.J.: Ablex, 73-99.
Fechner, G.T. (1860). Elemente der psychophysik. Leipzig: Breitkopf & Hartel. [Translation: Adler, H.E. (1966). Elements of Psychophysics. New York: Holt, Rinehart & Winston.].
Fisher, R.A. (1920). A mathematical examination of the methods of determining the accuracy of an observation by the mean error and by the mean square error. Monthly Notices of the Royal Astronomical Society,(53),758-770.
Fisher, W.P. & Wright, B.D. (1994). Applications of Probabilistic Conjoint Measurement. Special Issue. International Journal Educational Research, (21), 557-664.
Guttman, L. (1944). A basis for scaling quantitative data.
American Sociological Review,(9),139-150.
Guttman, L. (1950). The basis for scalogram analysis. In Stouffer et al. Measurement and Prediction, Volume 4. Princeton N.J.: Princeton University Press, 60-90.
Kolmogorov, A.N. (1950). Foundations of the Theory of Probability. New York: Chelsea Publishing.
Levy, P. (1937). Theorie de l'addition des variables aleatoires. Paris.
Linacre, J.M. & Wright, B.D. (1997). FACETS: Many-Faceted Rasch Analysis. Chicago: MESA Press.
Luce, R.D. & Tukey, J.W. (1964). Simultaneous conjoint measurement. Journal of Mathematical Psychology,(1),1-27.
Masters, G.N. & Wright, B.D. (1984). The essential process in a family of measurement models. Psychometrika, (49), 529-544.
Perline, R., Wright, B.D. & Wainer, H. (1979). The Rasch model as additive conjoint measurement. Applied Psychological Measurement, (3), 237-255.
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. [Danish Institute of Educational Research 1960, University of Chicago Press 1980, MESA Press 1993] Chicago: MESA Press.
Sears, S.D. (1997). A Monetary History of Iraq and Iran. Ph.D. Dissertation. Chicago: University of Chicago.
Smith, R.M. (1985). Validation of individual test response patterns. International Encyclopedia of Education, Oxford: Pergamon Press, 5410-5413.
Smith, R.M. (1986). Person fit in the Rasch Model. Educational and Psychological Measurement, (46), 359-372.
Smith, R.M. (1988). The distributional properties of Rasch standardized residuals. Educational and Psychological Measurement, (48), 657-667.
Smith, R.M. (1991). The distributional properties of Rasch item fit statistics. Educational and Psychological Measurement, (51), 541-565.
Smith, R.M. (1994). A comparison of the power of Rasch total and between item fit statistics to detect measurement disturbances. Educational and Psychological Measurement, (54), 42-55.
Stigler, S.M. (1986). The History of Statistics. Cambridge: Harvard University Press.
Thorndike, E.L. (1904). An introduction to the theory of mental and social measurements. New York: Teacher's College.
Thurstone, L.L. (1926). The scoring of individual performance. Journal of Educational Psychology, (17), 446-457.
Thurstone, L.L. (1927). A law of comparative judgement. Psychological Review, (34), 273-286.
Thurstone, L.L. (1928). Attitudes can be measured. American Journal of Sociology, (23), 529-554.
Thurstone, L.L. & Chave, E.J. (1929). The measurement of attitude. Chicago: University of Chicago Press.
Thurstone, L.L. (1931). Measurement of social attitudes. Journal of Abnormal and Social Psychology, (26), 249-269.
Wright, B.D. (1968). Sample-free test calibration and person measurement. Proceedings 1967 Invitational Conference on Testing Princeton: Educational Testing Service, 85-101.
Wright, B.D. (1977). Solving measurement problems with the Rasch model. Journal of Educational Measurement, (14), 97-116.
Wright, B.D. (1984). Despair and hope for educational measurement.
Contemporary Education Review, (1), 281-288.
Wright, B.D. & Linacre, J.M. (1989). Observations are always ordinal: measures, however, must be interval. Archives of Physical Medicine and Rehabilitation, (70), 857-860.
Wright, B.D. & Linacre, J.M. (1997). BIGSTEPS: Rasch Computer Program for All Two Facet Problems. Chicago: MESA Press.
Wright, B.D. & Masters, G.N. (1982). Rating Scale Analysis: Rasch Measurement. Chicago: MESA Press.
Wright, B.D. & Stone, M.H. (1979). Best Test Design: Rasch Measurement. Chicago: MESA Press.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo66.htm