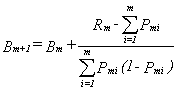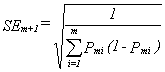Computer-Adaptive Testing:

A Methodology Whose Time Has Come.

 

By

 

John Michael Linacre, Ph.D.

MESA Psychometric Laboratory

University of Chicago

 

 

MESA Memorandum No. 69.

 

Published in Sunhee Chae, Unson Kang, Eunhwa Jeon, and J. M. Linacre. (2000)- Development of Computerized Middle School Achievement Test [in- Korean]. Seoul, South Korea: Komesa Press.
Table of Contents:

 

Introduction

 

1. A brief history of adaptive testing.

 

2. Computer-adaptive testing (CAT) - how it works.

(a) Dichotomous items.

(b) Polytomous items - rating scales and partial credit.

 

3. Computer-adaptive testing: psychometric theory and computer algorithms

 

4. Building an item bank.

 

5. Presenting test items and the test-taker's testing experience.

 

6. Reporting results.

(a) to the test-taker.

(b) for test validation.

 

7. Advantages of CAT.

 

8. Cautions with CAT.

 

Reference list.

 

Appendix: UCAT: A demonstration computer-adaptive program.

 

 

INTRODUCTION:

 

Computer-adaptive testing (CAT) is the more powerful successor to a series of successful applications of adaptive testing, starting with Binet in 1905.- Adaptive tests are comprised of items selected from a collection of items, known as an item bank.- The items are chosen to match the estimated ability level (or aptitude level, etc.) of the current test-taker.- If the test-taker succeeds on an item, a slightly more challenging item is presented next, and vice-versa.- This technique usually quickly converges into sequence of items bracketing, and converging on, the test-taker's effective ability level. The test stops when the test-taker's ability is determined to the required accuracy.- The test-taker may then be immediately informed of the test-results, if so desired.- Pilot-testing new items for the item bank, and validating the quality of current items can take place simultaneously with test-administration.- Advantages of CAT can include shorter, quicker tests, flexible testing schedules, increased test security, better control of item exposure, better balancing of test content areas for all ability levels, quicker test item updating, quicker reporting, and a better test-taking experience for the test-taker.- Disadvantages include equipment and facility expenses, limitations of much current CAT administration software, unfamiliarity of some test-takers with computer equipment, apparent inequities of different test-takers taking different tests, and difficulties of administering certain types of test in CAT format.

1. A BRIEF HISTORY OF ADAPTIVE TESTING.

 

In principle, tests have always been constructed to meet the requirements of the test-givers and the expected performance-levels of the test candidates as a group.- It has always been recognized that giving a test that is much too easy for the candidates is likely to be a waste of time, provoking usually unwanted candidate behavior such as careless mistakes or deliberately choosing incorrect answers that might be the answers to "trick questions".- On the other hand, questions that are much too hard, also produce generally uninformative test results, because candidates cease to seriously attempt to answer the questions, resorting to guessing, response sets and other forms of unwanted behavior.

 

There are other forms of adaptive testing, for instance tests that attempt to identify particular diagnostic profiles in the test-takers.- Such strictly diagnostic tests are not considered here, but the response-level results of performance-level tests often contain useful diagnostic information about test-takers.

 

Adjusting a test to meet the performance level of each individual candidate, however, has been viewed as problematic, and maybe unfair.- How are candidates to be compared if each candidate took a different test?

 

Alfred Binet (1905) achieved the major advance in this area with his intelligence tests.- Since his concern was with the diagnosis of the individual candidate, rather than the group, there was no issue of fairness requiring everyone to take the same test.- He realized he could tailor the test to the individual by a simple stratagem - rank ordering the items in terms of difficulty.- He would then start testing the candidate at what he deemed to be a subset of items targeted at his guess at the level of the candidate's ability.- If the candidate succeeded, Binet proceeded to give successively harder item subsets until the candidate failed frequently.- If the candidate failed the initial item subset, then Binet would administer successively easier item subsets until the candidate succeeded frequently.- From this information, Binet could estimate the candidate's ability level.- Binet's procedure is easy to implement with a computer.

 

Lord's (1980) Flexilevel testing procedure and its variants, such as Henning's (1987) Step procedure and Lewis and Sheehan's (1990) Testlets, are a refinement of Binet's method.- These can be conveniently operated by personal administration or by computer.- The items are stratified by difficulty level, and several subsets of items are formed at each level.- The test then proceeds by administering subsets of items, and moving up or down in accord with success rate on each subset.- After the administration of several subsets, the final candidate ability estimate is obtained.- Though a crude approach, these methods can produce usefully the same results as more sophisticated CAT techniques (Yao, 1991).

 

The use of computers facilitates a further advance in adaptive testing, the convenient administration and selection of single items.- Reckase (1974) is an early example of this methodology of computer-adaptive testing (CAT).- Initially, the scarcity, expense and awkwardness of computer hardware and software limited the implementation of CAT.- But now, in 2000, CAT has become common-place.

2. COMPUTER-ADAPTIVE TESTING (CAT) - HOW IT WORKS.

(A) DICHOTOMOUS ITEMS.

 

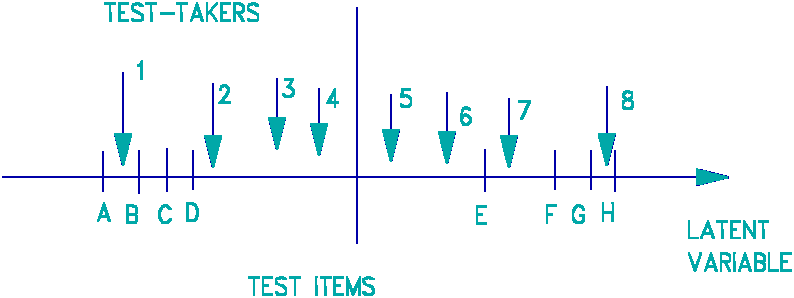
Imagine that an item bank has been constructed of dichotomous items, e.g., of multiple-choice questions (MCQs).- Every item has a difficulty expressed as a linear measure along the latent variable of the construct.- For ease of explanation, let us consider an arithmetic test.- The latent variable of arithmetic is conceptually infinitely long, but only a section of this range is relevant to the test and is addressed by items in the bank.- Let us number this section from 0 to 100 in equal-interval units.- So, every item in the bank has a difficulty in the range 0 to 100.- Suppose that 2+2=4 has a difficulty of 5 units. Children for whom 2+2=4 is easy have ability higher than 5 units.- Children for whom 2+2=4 is too difficult to accomplish correctly have ability below 5 units. Children with a 50% chance of correctly computing that 2+2=4 have an estimated ability of 5 units, the difficulty of the item.- This item is said to be "targeted on" those children.

 

Here is how a CAT administration could proceed.- The child is seated in front of the computer screen. Two or three practice items are administered to the child in the presence of a teacher to ensure that the child knows how to operate the computer correctly.- Then the teacher keys in to the computer an estimated starting ability level for the child, or, the computer selects one for itself.

 

Choice of the first question is not critical to measurement, but it may be critical to the psychological state of the candidate.- Administer an item that is much too hard, and the candidate may immediately fall into despair, and not even attempt to do well.- This is particularly the case if the candidate already suffers anxiety about the test.- Administer an item that is much too easy, and the candidate may not take the test seriously and so make careless mistakes.- Gershon (1992) suggests that the first item, and perhaps all items, should be a little on the easy side, giving the candidate a feeling of accomplishment, but in a situation of challenge.

 

If there is a criterion pass-fail level, then a good starting item has difficulty slightly below that.- Then candidates with ability around the pass-fail level are likely to pass, and to know that they passed, that first item and so be encouraged to keep trying.-

 

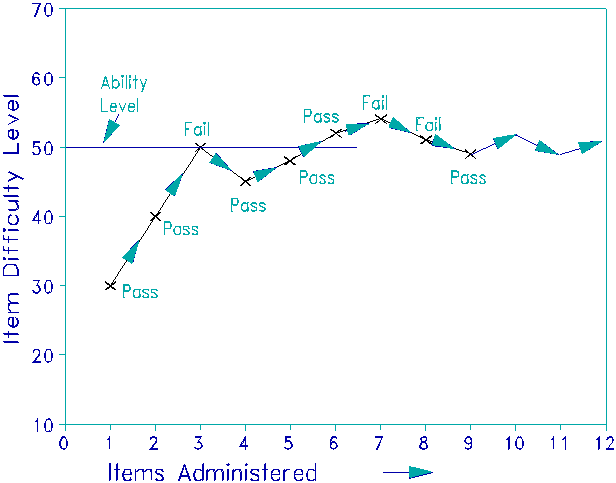
In our example, suppose that the first item to be administered is of difficulty 30 units, but that the child has ability 50 units.- The child will probably pass that first item.- Let's imagine that happens (see Figure 1).- The computer now selects a more difficult item, one of 40 units.- The child passes again.- The computer selects a yet more difficult item, one of 50 units.- Now the child and the item are evenly matched.- The child has a 50% chance of success.- Suppose the child fails.- The computer administers a slightly easier item than 50 units, but harder than the previous success at 40 units.- A 45 unit item is administered.- The child passes.- The computer administers a harder item at 48 units.- The child passes again.- In view of the child's success on items between 40 and 48 units, there is now evidence that the child's failure at 50 may been unlucky.

 

The computer administers an item of difficulty 52. This item is only slightly too hard for the child. The child has almost a 50% chance of success.- In this case, the child succeeds.- The computer administers an item of difficulty 54 units.- The child fails. The computer administers an item of 51 units.- The child fails.- The computer administers an item of 49 units.- The child succeeds.

 

 

This process continues.- The computer program becomes more and more certain that the child's ability level is close to 50 units.- The more items that are administered, the more precise this ability estimate becomes.- The computer program contains various criteria, "stopping rules", for ending the test administration.- When one of these is satisfied, the test stops. The computer then reports (or stores) the results of that test.- The candidate is dismissed and the testing of the next candidate begins.

 

There are often other factors that also affect item selection.- For instance, if a test address a number of topic areas, then content coverage may require that the test include items be selected from specific subsets of items.- Since there may be no item in the subset near the candidate's ability level, some content-specific items may be noticeably easier or harder than the other items.- It may also be necessary to guard against "holes" in the candidate's knowledge or ability or to identify areas of greater strength or "special knowledge".- The occasional administration of an out-of-level item will help to detect these.- This information can be reported diagnostically for each candidate, and also used to assist in pass-fail decisions for marginal performances.

 

The dichotomous test is not one of knowledge, ability or aptitude, but of attitude, opinion or health status, then CAT administration follows the same plan as above.- The difference is that the test developer must decide in which direction the variable- is oriented.- Is the answer to be scored as "right" or "correct" to be the answer that indicates "health" or "sickness"?- Hire "right" or "correct" is to be interpreted to be "indicating more of the variable as we have defined the direction of more-ness." The direction of scoring will make no difference to the reported results, but it is essential in ensuring that all items are scored consistently in the same direction.- If the test is to screen individuals to see if they are in danger of a certain disease, then the items are scored in a direction such that more danger implies a higher score.- Thus the "correct" answer is the one indicating the greater danger.

 

 

2. COMPUTER-ADAPTIVE TESTING (CAT) - HOW IT WORKS.

-(B) POLYTOMOUS ITEMS: RATING SCALES AND PARTIAL CREDIT.

 

In principle, the administration of a polytomous item is the same as that of a dichotomous item.- Indeed, typically the test-taker would not be able to discern any difference between a strictly dichotomous MCQ and a partial-credit MCQ one.- The difference, in this case, is in the scoring.- Some distractors are deemed to be more nearly correct than others, and so are given greater scores, i.e., credit.- The correct option is given the greatest score.- These different partial-credit scores are numerically equivalent to the advancing categories of a rating scale of performance on the item.

 

If the CAT administration is intended to measure attitude, the rating scale presented to the test-taker may be explicit.- Here, the scoring of the rating scale categories is constructed to align with the underlying variable as it has been defined by the test constructor.- For each item, the categories deemed to indicate more of that variable, whether oriented towards "sickness" or "health", are assigned to give greater scores.

 

Item selection for polytomous items presents more of a challenge than for dichotomous items.- There is not one clear difficulty for each item, but rather a number of them, one for each inter-category threshold.- Generally speaking, the statistically most efficient test is one in which the items are chose so that their middle categories are targeted at the test-taker's ability level.- But this produces an uncomfortable test-experience and an enigmatic report.- On an attitude survey comprised of Likert scales (Strongly Agree, Agree, Neutral, Disagree Strongly Disagree), it may mean that every response was in the Neutral category.- On partial-credit math items, it may mean that every response was neither completely wrong, nor completely right.- Under these circumstances, it is a leap of faith to say what the candidate's attitude actually is, or what the test-taker can actually do successfully, or fail to do entirely.

 

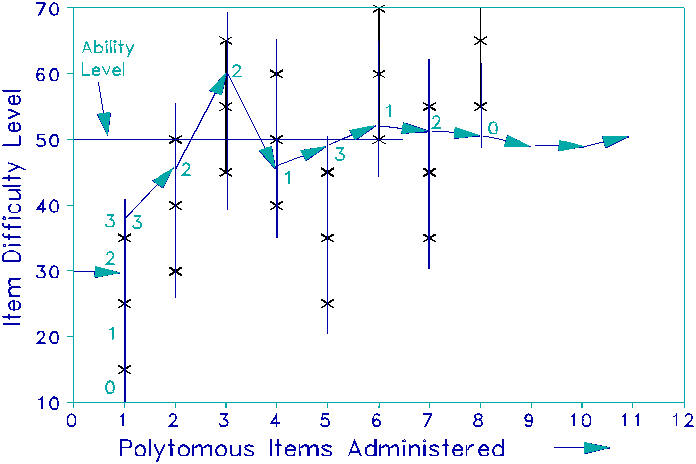
Accordingly, item selection for polytomous items must consider the full range of the rating or partial credit scales, with a view to targeting the test-taker at every level.- Figure 2 gives an

 

example.

 

In Figure 2, the item bank consists of partial-credit or rating-scale items with four levels of performance, scored 0, 1, 2, 3, and with the same measurement scale structure.- In practice, polytomous item banks can contain mixtures of items with different rating scales and also dichotomies.- Again the test-taker ability (or attitude, etc.) is 50 units.- Again, the first item is targeted to be on the easier side, but still challenging, for someone with an ability of 30 units.- In fact, someone with an ability of 30 units would be expected to score a "2" on this item.- Our candidate gets the item right and scores a "3".- The category threshold between a "2" and a "3" on this item is at 35, so our candidate is estimate to be slightly more able than that threshold at 38.- Since the first item proved to be on the easier side for our candidate, the second item is deliberately targeted to be slightly harder.- An item is chosen on which the candidate is expected to score "1".- The candidate scores "2".- The 3rd item is chosen to be yet harder.- The candidate scores "2" again.- With the 4th item, an attempt is made to find what is the highest level at which the candidate can obtain complete success.- An easier item is administered for which the candidate may be able to score in the top category.- The candidate fails, only scoring a "1".- For the 5th item, another attempt is made to find at what level the candidate can score in the top category.- An easier item is administered.- The candidate answers in the top category and obtains a "3".-

 

Now an attempt is made to find out how hard an item must be before the candidate fails completely. Item 6 is a much harder item.- The candidate scores a "1".- Since we do not want to dishearten the candidate, a less difficult, but still challenging item is given as Item 7.- The candidate scores a "2".- Then again a much harder item is given as Item 8.- The candidate scores a "0".- The test continues in this same way developing a more precise estimate of candidate ability, along with a diagnostic profile of the candidate's capabilities on items of all relevant levels of difficulty.- The test ceases when the "stopping rule" criteria are met.

 

Since polytomous items are more informative of candidate performance than dichotomous items, polytomous CAT administrations usually comprise fewer items.- Writing polytomous items, and developing defensible scoring schemes for them, can be difficult.- They can also require that more time and effort be expended by the candidate on each item.- Accordingly, it can be expected that large item banks are likely to include both types of item.

 

3. COMPUTER-ADAPTIVE TESTING: PSYCHOMETRIC THEORY AND COMPUTER ALGORITHMS

 

Choice of the Measurement Model

 

An essential concept underlying almost all ability or attitude testing is that the abilities or attitudes can be ranked along one dimension. This is what implied when it is reported that one candidate "scored higher" than another on a certain test.- If scores on a test rank candidates in their order of performance on the test, then the test is being used as though it ranks candidates along a unidimensional variable.

 

Of course, no test is exactly unidimensional.- But if candidates are to be ranked either relative to each other, or relative to some criterion levels of performance (pass-fail points), then some useful approximation to unidimensionality must be achieved.

 

Unidimensionality facilitates CAT, because it supports the denotation of items as harder and easier, and test-takers as more and less able, regardless of which items are compared with which test-takers.- Multidimensionality confounds the CAT process because it introduces ambiguity about what "correct" and "incorrect" answers imply.- Consider a math "word problem" in which the literacy level required to understand the question is on a par with the numeracy level required to answer the question correctly.- Does a wrong answer mean low literacy, low numeracy or both?- Other questions must be asked to resolve this ambiguity, implying the multidimensional test is really two unidimensional tests intertwined.- Clearly, if the word problems are intended to be a math test, and not a reading test, the wording of the problems must be chosen to reduce the required literacy level well below that of the target numeracy level of the test.- Nevertheless, investigations into CAT with multidimensionality are conducted (van der Linden, 1999).

 

Since it can be demonstrated that the measurement model necessary and sufficient to construct a unidimensional variable is the Rasch model (e.g., Wright, 1988), the discussion of CAT algorithms will focus on that psychometric model.- Even when other psychometric models are chosen initially because of the nature of pre-existing item banks, the constraints on item development in a CAT environment are such that a Rasch model must then be adopted.- This is because test-takers are rarely administered items sufficiently off-target to clearly signal differing item discriminations, lower asymptotes (guessing) or higher asymptotes (carelessness).- Similarly, it is no longer reasonable to assert that any particular item was exposed to a normal (or other specified) distribution of test-takers.- Consequently, under CAT conditions, the estimation of the difficulty of new items is reduced to a matter of maintaining consistent stochastic ordering between the new and the existing items in the bank.- The psychometric model necessary to establish and maintain consistent stochastic ordering is the Rasch model (Roskam and Jansen, 1984).

 

The dichotomous Rasch model presents a simple relationship between the test-takers and the items.- Each test-taker is characterized by an ability level expressed as a number along an infinite linear scale of the relevant ability.- As with physical measurement, the local origin of the scale is chosen for convenience.- The ability of test-taker n is identified as being B_n units from that local origin.- Similarly each item is characterized by a difficulty level also expressed as a number along the infinite scale of the relevant ability.- The difficulty of item i is identified as being D_i units from the local origin of the ability scale.

 

A concern can arise here that both test-takers and items are being located along the same ability scale.- How can the items be placed on an ability scale?- At a semantic level, Andrich (1990) argues that the written test items are merely surrogate, standardized examiners, and the struggle for supremacy between test-taker and item is really a struggle between two protagonists, the test-taker and the examiner.- At a mathematical level, items are placed along the ability metric at the points at which those test-takers have an expectation of 50% success on those items.

 

This relationship between test-takers and items is expressed by the dichotomous Rasch model (Rasch, 1960/1992):

 

where P_ni1 is the probability that test-taker n succeeds on item i, and P_ni0 is the probability of failure.-

The natural unit of the interval scale constructed by this model is termed the logit (log-odds unit).- The logit distance along the unidimensional measurement scale between a test-taker expected to have 50% success on an item, (i.e., at the person at same position along the scale as the item,) and a test-taker expected to have 75% success on that same item is log_e(75%/25%) = 1.1 logits.

 

From the simple, response-level Rasch model, a plethora of CAT algorithms have been developed.

 

The Design of the Algorithm

 

In essence, the CAT procedures is very simple and obvious.- A test-taker is estimated (or guessed) to have a certain ability.- An item of the equivalent level of difficulty is asked.- If the test-taker succeeds on the item, the ability estimate is raised. If the test-taker fails in the item, the ability estimate is lowered.- Another item is asked, targeted on the revised ability estimate.- And the process repeats.- Different estimation algorithms revise the ability estimate by different amounts, but it has been found to be counter-productive to change the ability estimate by more than 1 logit at a time. Each change in the ability estimate is smaller, until the estimate is hardly changing at all. This provides the final ability estimate.

 

Stopping Rules

 

The decision as to when to stop a CAT test is the most crucial element.- If the test is too short, then the ability estimate may be inaccurate.- If the test is too long, then time and resources are wasted, and the items exposed unnecessarily.- The test-taker also may tire, and drop in performance level, leading to invalid test results.

 

The CAT test stops when:

 

1. the item bank is exhausted.

This occurs, generally with small item banks, when every item has been administered to the test-taker.

 

2. the maximum test length is reached.

There is a pre-set maximum number of items that are allowed to be administered to the test-taker.- This is usually the same number of items as on the equivalent paper-and-pencil test.

 

3. the ability measure is estimated with sufficient precision.

Each response provides more statistical information about the ability measure, increasing its precision by decreasing its standard error of measurement.- When the measure is precise enough, testing stops.- A typical standard error is "0.2 logits.

 

4. the ability measure is far enough away from the pass-fail criterion.

For CAT tests evaluating test-takers against a pass-fail criterion level, the test can stop once the pass-fail decision is statistically certain.- This can occur when the ability estimate is at least two S.E.'s away from the criterion level, or when there are not sufficient items left in the test for the candidate to change the current pass-fail decision.

 

5. the test-taker is exhibiting off-test behavior.

The CAT program can detect response sets (irrelevant choice of the same response option or response option pattern), responding too quickly and responding too slowly.- The test-taker can be instructed to call the test supervisor for a final decision as to whether to stop or postpone the test.

 

The CAT test cannot stop before:

 

1. a minimum number of items has been given.

In many situations, test-takers will not feel that they have been accurately measured unless they have answered at least 10 or 20 items, regardless of what their performances have been.- They will argue, "I just had a run of bad luck at the start of the test, if only you had asked me more questions, my results would have been quite different!"

 

2. every test topic area has been covered.

Tests frequently address more than one topic area.- For instance, in arithmetic, the topic areas are addition, subtraction, multiplication and division.- The test-taker must be administered items in each of these four areas before the test is allowed to stop.

 

3. sufficient items have been administered to maintain test validity under challenge or review.

This can be a critical issue for high-stakes testing.- Imagine that the test stops as soon as a pass or fail decision can be made on statistical grounds (option 4, above).- Then those who are clearly expert or incompetent will get short tests, marginal test-takers will get longer tests.- Those who receive short tests will known they have passed or failed.- Those who failed will claim that they would have passed, if only they had been asked the questions they know.- Accordingly it is prudent to give them the same length test as the marginal test-takers.- The experts, on the other hand, will also take a shorter test, and so they will know they have passed.- This will have two negative implications.- Everyone still being tested will know that they have not yet passed, and may be failing.- Further, if on review it is discovered there is a flaw in the testing procedure, it is no longer feasible to go back and tell the supposed experts that they failed or must take the test again. They will complain, "why didn't you give me more items, so that I could demonstrate my competence and that I should pass, regardless of what flaws are later discovered in the test."

 

An Implemented Computer-adaptive Testing Algorithm

 

 

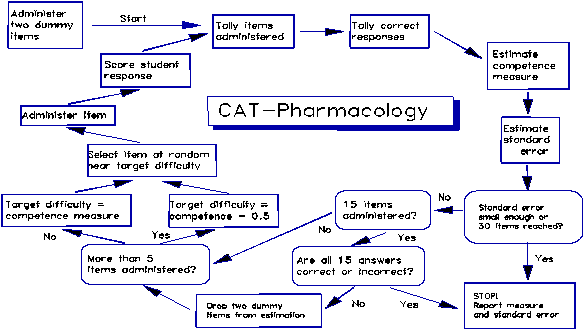
Figure 4. A CAT Item Administration Algorithm (Halkitis, 1993).

 

Halkitis (1993) presents a computer-adaptive test designed to measure the competency of nursing students in three areas: calculations, principles of drug administration and effects of medications.- According to Halkitis, it replaced a clumsy paper-and-pencil test administration with a stream-lined CAT process.

 

For each content area, an item bank had been constructed using the item text and item difficulty calibrations obtained from previous paper-and-pencil tests administered to 4496 examinees.

 

As shown in Figure 3, as CAT administration to a test-taker begins, an initial (pseudo-Bayesian) ability estimate is provided by awarding each student one success and one failure on two dummy items at the mean difficulty, D₀, of the sub-test item bank.- Thus each student's initial ability estimate is the mean item difficulty.

 

The first item a student sees is selected at random from those near 0.5 logits less than the initial estimated ability.- This yields a putative 62% chance of success, thus providing the student, who may not be familiar with CAT, extra opportunity for success within the CAT framework.- Randomizing item selection improves test security by preventing students from experiencing similar tests.- Randomization also equalizes bank item use.

 

After the student responds to the first item, a revised competency measure and standard error are estimated.- Again, an item is chosen from those near 0.5 logits easier than the estimated competency.- After the student responds, the competency measure is again revised and a further item selected and administered.- This process continues.

 

After each m responses have been scored with R_m successes, a revised competency measure, B_m+1, is obtained from the previous competency estimate, B_m, by:

 

The logit standard error of this estimate, SE_m+1, is

 

P_mi is the modelled probability of success of a student of ability B_m on the i^th administered item of difficulty D_i,

The initial two dummy items (one success and one failure on items of difficulty D₀) can be included in the summations.- This will reduce the size of the change in the ability estimate, preventing early nervousness or luck from distorting the test.

 

Beginning with the sixth item, the difficulty of items is targeted directly at the test-taker competency, rather than 0.5 logits below.- This optimal targeting theoretically provides the same measurement precision with 6% fewer test items.

 

If, after 15 responses, the student has succeeded (or failed) on every administered item, testing ceases.- The student is awarded a maximum (or minimum) measure.- Otherwise, the two dummy items are dropped from the estimation process.

 

There are two stopping rules.- All tests cease when 30 items have been administered.- Then the measures have standard errors of 0.4 logits.- Some tests may end sooner, because experience with the paper-and-pencil test indicates that less precision is acceptable when competency measures are far from mean item bank difficulty.- After item administration has stopped, the competency estimate is improved by several more iterations of the estimation algorithm to obtain a stable final measure.- This measure and its standard error are reported for decision making.

 

Simpler CAT Algorithm

 

Wright (1988) suggests a simpler algorithm for classroom use or when the purpose of the test is for classification or performance tracking in a low-stakes environment.- This algorithm is easy to implement, and could be successfully employed at the end of each learning module to keep track of student progress.

 

Here are Wright's (1988) core steps needed for practical adaptive testing with the Rasch model:

1. Request next candidate. Set D=0, L=0, H=0, and R=0.

2. Find next item near difficulty, D.

3. Set D at the actual calibration of that item.

4. Administer that item.

5. Obtain a response.

6. Score that response.

7. Count the items taken: L = L + 1

8. Add the difficulties used: H = H + D

9. If response incorrect, update item difficulty: D = D - 2/L

10. If response correct, update item difficulty: D = D + 2/L

11. If response correct, count right answers: R = R + 1

12. If not ready to decide to pass/fail, Go to step 2.

13. If ready to decide pass/fail, calculate wrong answers: W = L - R

14. Estimate measure: B = H/L + log_e(R/W)

15. Estimate standard error of the measure: S = %[L/(R*W)]

16. Compare B with pass/fail standard T.

17. If (T - S) < B < (T + S), go to step 2.

18. If (B - S) > T, then pass.

19. If (B + S) < T, then fail.

20. Go to step 1.

 

 

UCAT: CAT with Item Bank Recalibration

 

Linacre (1987) addresses the problem of adding new test items to the item bank, and recalibrating the bank.- Essentially the same algorithm for test administration is employed as that presented in Halkitis (1993) and shown above.- An extra program component is added, however, for bank recalibration.- The CAT test developer or the CAT administrator can choose to have the difficulties of the items in the bank recalibrated at any point based on the responses of those to whom the items have been administered so far.- As part of the recalibration procedure, all test-takers are remeasured based on their original responses and the revised item difficulties.- The final revised item calibrations are computed in such a way as to maintain unchanged the mean of the ability estimates of those who have already taken the test.- The minimizes the effect of the recalibration on any previously reported test results.

 

This algorithm has two conspicuous virtues.- New items can be introduced into the bank at any time.- As Wright and Douglas (1975) point out, and Yao (1991) confirms, poor calibration of a few items is not deleterious to Rasch measurement.- Consequently the difficulty level of the new items can be guessed intelligently without degrading the resulting ability estimates.- The degradation of measures by poor item calibration is further diminished by the self-correcting nature of CAT.

 

Secondly, existing items can be recalibrated with minimal impact on previous test-taker measures.- This is especially important when the item difficulty calibrations are derived from non-CAT sources, or when there is concern that part of the item bank has become public knowledge.

 

The BASIC source code for this CAT program, named UCAT, is presented in the Appendix.- Here is the information that accompanies the program.

 

What taking a UCAT test looks like

 

Figure 4 shows a multiple choice question as it appears on the test-taker's computer screen.- The text for this screen was read from the question file, an item bank.- The computer selects which questions to administer.- Each question has a one-line question text, and five alternative answers.- The test-taker presses the number on the keyboard matching the chosen answer.- The computer then asks another question, until it has measured the test-taker's ability precisely enough.

 

At the end of the test session the computer displays a summary report like Figure 5.- Each line shows the identifying number of a question that was administered, its difficulty measurement, the answer selected, and whether the answer was right or wrong.- If the answer was quite contradictory to the test-taker's estimated ability, because either a very easy question was got wrong or a very hard question was got right, the word "SURPRISINGLY" is displayed in front of "RIGHT" or "WRONG". "SURPRISINGLY" can indicate many things:- lucky guesses, careless slips, special knowledge or even mistakes in writing the questions.- Feedback like this has proved useful to both students and teachers (Bosma, 1985)

 

 

 

What the computer is doing during the test

 

On starting the test, the program assumes the test-taker's ability measure to be near the mid-range of ability, 100 units.- A question of around 100 units is asked. While the test-taker is reading the question, the computer calculates what that ability estimate would be if the question is failed, and also what the ability would be if the test-taker succeeds.- It then selects from the item bank a question between these estimates.- This will be the next question it asks.- Meanwhile, the test-taker finishes reading the first question, and keys in the number corresponding to the choice of correct answer.- The computer checks whether this answer is scored as correct or incorrect, and updates the ability estimate with one of the new estimates it has already calculated.- It immediately displays the question already chosen to be next. The test-taker starts reading this question and the computer sets about calculating possible ability levels and choosing a question to give next.- The test-taker keys in an answer once more.- This process continues until the computer has calculated the test-taker's ability sufficiently precisely.

 

At the end of the test, the computer displays a summary report of how the test-taker did.- It also adds this report to the test history file on disk, which is used for re-estimating the difficulty of test items.- For everyone who takes the test, the computer records name, estimated ability, each question asked, answer chosen, and whether it was correct.- The computer also reports whether this particular response is much as expected, whether right or wrong, or surprisingly right (perhaps a lucky guess), or surprisingly wrong (perhaps a careless error).

 

 

Constructing the file of questions

Frequently, the hardest part of the testing process is constructing the questions and the distractors, the alternate wrong answers.- Figure 6 shows the first few questions in a file of geography questions.- This can be typed in using a word processor and saved as a text file.- Question file item banks can be built for whatever topic areas are desired.- Each file should contain questions for only one area, such as geography or math, so that UCAT measures ability in only one area at a time.- The questions in the item bank follow the layout in Figure 6.

 

Each question has 10 lines.- The first line is a question identifying number for reference.- Numbers must be in ascending order, but not every number has to be used, so that questions can be added or deleted from the question file as the test is developed.- The second line is the question, which can be up to 250 characters long.- \ is used to continue the question on the next line. @ also continues the question, but forces the next line to appear on the next line of the test-taker's screen. The third through the seventh lines each have one of the five alternative answers, one of which must be the correct one, again each answer can be up to 250 characters long.- The usual rules for writing multiple-choice tests apply, such as avoiding having two correct answers, no correct answers, or answers that do not fit in with the grammar of the question.- On the eighth line is the option number of the correct choice of answer:- 1,2,3,4 or 5.- "1" means the first of the five alternatives is the correct answer.- If this scoring key is wrong, the program will report numerous surprisingly wrong answers when competent test-takers consistently fail to select the incorrectly specified "right" answer.

 

 

On the ninth line, the item difficulty may initially be an educated guess.- One problem with a new test is that it is not known precisely know how difficult the questions are.- But, after a few people have taken the test, the computer can re-estimate the questions' difficulties.- In order to start the estimation process, initial values are needed. The ninth line of each question contains an initial estimate of the difficulty of the question just written.- This will be a number in the range of 1 to 200 with 100 being "average" difficulty.- Hard questions could start at 120.- Easy ones at 80.- If there is no theoretical or empirical information at all about the item's difficultly, you it is entered at 100.- The computer may substantially alter this initial estimate later, when asked to re-estimate item difficulties.

 

Finally, the tenth line blank is left blank. The next question follows in the same format.

 

As many questions as desired may be entered in the item bank, the file of test questions. Twenty questions is a good starting point.- More questions can be added at any time, but when questions are added or changed, new, later numbers must be assigned numbers, so that the program does not get confused between an original question, now deleted or changed, and a new question which happens to have the same identifying number.

 

Improving ability measurements - re-estimating question difficulties

 

 

There is a test history file on disk which can be inspected with a text editor or word processor.- An example is shown in Figure 7.- It contains a complete log_e of each testing session.

 

After several people have taken the test, UCAT can re-estimate the difficulty levels of the questions and also re-estimate the previous test-takers' abilities, so that they more closely correspond with the way the test is behaving overall. -This is done in much the same way as test-taker abilities are estimated when they take the test.- Once new difficulty and ability estimates have been calculated, they are included in the question and test history files and written out to disk.- Figure 8 shows how the new question difficulty and its range is included before the previous difficulty estimate in the question file.- Figure 9 shows how the revised test-taker ability estimate and range is included before the previous ability and range in the test history file.

 

 

 

 

 

 

 

Detailed explanation of the BASIC program

 

This is a detailed narrative of how UCAT uses the question file and conducts a test.- This can be understood in concert with the BASIC listing in the Appendix.- The name and purpose of each BASIC variable is stated as a comment at the start of the program.- Comments start with a '.

 

Line 10 is the conversion function between the natural unit, logits, and the unit for reporting.- Typically a conversion similar to 10 user units per logit is employed.- This means that important differences are expressed as integer units, rather decimal fractions.

 

Line 20 begins a block of code that decodes the control options available for UCAT.- These are listed at the start of the program listing.- Options /D /S display all information to the screen.- This is convenient when UCAT is being used to demonstrate CAT. The /A parameter sets the precision with which an ability is estimated. This is known, statistically, as the standard error of estimation.- It indicates the size of the zone above and below your ability estimate in which your true ability probably lies.- All measuring techniques have some sort of standard error associated with them, but it is usually not reported and so measurements are frequently thought to be more exact than they really are.- In this program, the maximum standard error is set at about .7 logits, so that if an ability is reported as 100 units, the true ability is probably between 93 to 107.- This program ignores the standard error of the item difficulties, which could increase the size of the probable zone by 20%, but probably less (Wright and Panchapakesan, 1969).

 

Line 30 establishes the maximum number of persons to be maintained in the test-taker file.- This can be increased at any time. The random number generator is initialized.- This program uses random numbers to give everyone a different series of questions which meet the test requirements.

 

Line 40 request the name of the question file or item bank.

 

Line 50 calls the subroutine at line 850. This reads in the question file which must be in the format of Figure 6.- UCAT supports a simple question file encryption security procedure.- This prevents computer-savvy test-takers from deviously reading the question file with its answer key. If the question file is encrypted, it has the suffix ".SEC".- Following the UCAT program listing is that of the program SECURE.BAS which effects this simple encryption and matching decryption.

 

The subroutine at line 850 counts up how many items are in the bank, and how many response options each item has.- These numbers are reported at line 60.

 

At line 70, the necessary internal data arrays for test-takers (persons) and items are allocated.- The item text is read into the arrays at line 80, subroutine 870. The 10 lines of text corresponding to each question are loaded into the question text array.- A check is made to insure that the indicated correct answer on line 8 of the item text is in the range, 1 to 5, of valid options.- The question difficulty on line 9 of the item text is converted from external units to logits and checked that it is between 1 and 200 units. If an error is found the program stops and reports the approximate line number where the error was found.

 

At line 90 of the program, the output file of test-taker information is identified.- This can be a pre-existing file to which new test-taker information is to be added.- Responses in this file will be used to re-estimate item difficulties.

 

At line 120, test administration begins with a call to subroutine 180.- This continues until all the testing session concludes.- At line 130, the test administrator has the opportunity to re-estimate item difficulties, resume testing or conclude the program.

 

This program can be used for giving tests in other topic areas by specifying different question and test history files.

 

Test Session Program Logic

 

A testing session starts in line 180.- The name of the test-taker is entered, followed by the Enter (Return) key.-- The Enter (Return) key must always be pressed in order for the computer to accept a response.

 

In line 200, the computer randomly assigns a lower limit to your ability about between ‑1.0 and ‑0.5 logits below the mean item difficulty.- The program uses the logit for its internal units to simplify the math.- The initial upper limit to your ability estimate is put 1 logit higher.- The initial standard error of the ability estimate is assumed to be the desired final precision level.

 

The computer then flags all questions as unasked in line 220, initializes the counters of questions asked and the test-taker's score so far, and selects the first question.-

 

The question selection subroutine, in line 460, sets the selected question to zero.- If the current standard error is better than the required accuracy, or all the questions in the question file have been asked, there is an immediate return without selecting another question.- The question file is in its original order. In order not to tend to give questions in the same sequence of questions, a random number generator is used to provide the position in the question array from which to start looking for a question that meets the selection algorithm's requirements.- A question is needed that has not been asked, and whose difficulty is between the higher and lower ability estimates.- Such a question is of a difficulty appropriate to the current estimate of test-taker ability.- When a suitable question is found, the subroutine concludes. If no suitable question is found in the array, the unasked question, closest in difficulty to the test-taker's ability, is used.- The algorithm can be adjusted by the user to control content area coverage, reduce item exposure, check for knowledge gaps and special knowledge, or to increase test efficiency.

 

If a question has been found, which should always happen the first time, the program goes to the subroutine at line 330.- This displays the question and its possible answers on the screen.- Though each line of text in the question file (the question itself and the possible answers) only occupies one logical line, these lines can be up to 250 characters long.- The display routine at line 313 splits them into several lines on the screen.- It also updates the various arrays to show this question has been asked, but does not wait for the test-taker's.-

 

In line 380, the computer calculates an expected score based on the previous ability estimate and the difficulty of the items encountered so far, including the one just presented.- The expected score is the sum of the probabilities of success on the questions, based on the test-taker's estimated ability and the difficulties of the items.-- The standard error of the ability estimate is obtained by first calculating the raw score variance, which is the sum of the product of the probability of success and the probability of failure on each question.- The standard error of the ability estimate is the reciprocal of the square root of that variance.

 

At this point, two actual scores are possible.- The test-taker can get the question displayed on the screen right or wrong.- First, UCAT assumes that the answer will be wrong, so that the total count of correct answers, the score so far, will not change.- In line 430, this gives a low ability estimate which, is found by adjusting the previous estimate by the difference between the observed score and the expected, divided by the expected score variance.- However to guard against the ability estimate changing too quickly due to careless mistakes or other quirks, this variance is never allowed to become less than one.- The test-taker's ability is than calculated for a correct answer to the current question.- This gives a higher estimate of ability, obtained by adding to the low ability estimate the logit value of one more right answer.

 

On returning to the main program at line 250, the your response to the question just displayed is still not known.- UCAT assumes it is going to take some time for you to read all the text that has been displayed and to make a decision, so it goes to the subroutine at line 460 to select the next question to be displayed.- That question is selected, in the same way as the first question, by starting at a random point in the question file and selecting the first question between the high and low ability estimates.

 

Again at line 250, the subroutine at line 540 is called. It returns to the screen to discover what answer has been given to the question that has been displayed.- Only a number in the range 1 to 5 is allowed (followed by pressing the Enter key).- After receiving a selection, the computer notes it in an array, and, if it is correct, increments the test-taker's raw score and replaces the newly calculated low ability estimate with the high ability estimate.- This "low" ability estimate is now the current best estimate of the test-taker's ability.

 

The test can be stopped now, or at any time, by pressing the Ctrl and S keys together and then Enter.- This is useful if the administrator wants to stop the test early.

 

Back to line 250, and, if a new question has been selected, the computer repeats the process by displaying the next question.- If no question has been selected, either because there are none left, or, more desirably, because the current standard error of estimation is smaller than the accuracy required, the ability estimate is refined by one more re-estimation cycle in line 270. In the subroutine at line 380, there is no increase in the number of questions asked so that, what before was the low estimate of ability, now becomes the most likely estimate of ability.

 

At line 280, the computer displays a message that the test is completed, and, if in supervisor mode, displays, using the subroutine at 610, the likely values of the test-taker's ability measurement.

 

When the test supervisor returns to the keyboard, all the questions taken and results obtained so far are displayed with the subroutine at line 640. This information is written, in even more detail, onto the test history file.- The word "SURPRISINGLY" is added, in line 760,- to those answers which represent an unexpected right or wrong response to a question which is more than 2 logits harder or easier than the ability estimate.

 

At this point another test can be given, or the question difficulties re-estimated. When the question file is first constructed, it may have been necessary to guess which are the easy and hard questions, and particularly what difficulty values to give them.- However, after twenty or so people have taken the test, it may improve test validity and efficiency to have the computer to re-estimate the difficulty levels of your questions based on the responses they have actually received.

 

UCAT does this when re-estimation is request at line 130.- In the subroutine at 960, it reads the test history file, and notes for each person what ability they were estimated to have and which questions they answered correctly and incorrectly.- The reason for obtaining the test-taker's ability estimates is to provide a starting point for the re-estimation procedure, and also to enable UCAT to keep the same mean ability for the test-takers.- This is so that the re-estimation procedure will alter their ability estimates as little as possible.- After reading in the responses, UCAT ignores all test-takers and questions for which there is not at least one right and one wrong answer.- For a big question file, it may take many test administrations before all questions can be re-estimated.

 

UCAT now refines the estimates, starting in line 1340, in the same way it did when calculating abilities, but this time the question difficulties and test-taker abilities are adjusted simultaneously. This is done through 10 cycles of re-estimation, after which there are generally no significant differences between any pair of expected and observed scores.- During this procedure, at line 1480, the average test-taker ability is maintained constant in order to minimize changes in the test-takers' estimates.

 

After the re-estimation procedure is completed at line 1550, the question file is written to disk with the new difficulty estimate, and probable range inserted at the front of the ninth line of each question.- A copy of the test history file is also made, adding, in line 1700, a revised test-taker ability estimate and its probable range.- At line 1730, a response data matrix is written for use by other item analysis programs.- After re-estimation, testing can be resumed, if desired.

 

4. BUILDING AN ITEM BANK.

 

A necessary pre-requisite to computer-adaptive testing is an item bank (Wright and Bell, 1984).- An item bank is an accumulation of test items.- There is the text of the item, details of correct and incorrect responses to it, and its current difficulty estimate.- If the item has a rating scale or internal scoring structure, that is also included.- There may also be indicators of item content area, instructional grade level and the like.- It is usual also to include details of the history of the items development, use and recalibration.

 

Initially CAT item banks usually contain items given under conventional paper-and-pencil conditions.- For any particular test in that format, every item has been given to every test-taker.- This enables at least a p-value (percent of success on the item for the sample) for each item to be computed.- An initial estimate of the logit difficulty of an item within a test form then becomes log_e(100-pvalue / pvalue).- Available Rasch software, e.g., BIGSTEPS (Linacre and Wright, 1988) enables production of better initial item difficulty estimates.- Test equating procedures (Wright and Stone, 1979) enable the difficulties of all items to be estimated within one common frame of reference.- These items can then be entered into an item bank, and CAT administration begun fairly quickly.- Studies have indicated that most paper-and-pencil items maintain their difficulty level when transferred to CAT.- Exceptions are items with idiosyncratic presentation requirements.- For instance, some figures and graphical plots are easier to think about (and make annotations on) when they are presented horizontally on a paper-and-pencil test, than when they are presented vertically on a CAT computer screen.

 

When an item bank is to be constructed out of newly composed items, difficulty levels must be assigned other than directly from p-values or quantitative item analysis. Stratifying or ordering items by difficulty has two aspects.- First, there is ordering based on the theoretical construct.- Experts in a field generally know what topic areas should be harder than others for those at any stage of development.- This enables an ordering of items by topic area difficulty.- In addition, inspection of individual items gives indications of their relative difficulty.- Consequently, a fairly robust stratifying of items by expert-perceived difficulty can often be accomplished.- There are situations, however, when there is no clear construct-based ordering.- A multiple-choice question (MCQ) may be written with its incorrect options, i.e., distractors, so close to, or far from, the correct answer as to render the item much harder, or much easier, than it should be according to its construct level.

 

Second, there is ordering based on empirical performance of a previous sample of test candidates.- For brand new items, this does not exist, but it is often possible to identify similar pre-existing items.- Then the difficult levels of these items can be used.

 

For larger scale testing, testing agencies often enter into CAT with an accumulation of items of uncertain quality and dimensionality.- An advantage of the CAT approach is that changes to the item bank can be made at any point in test administration.- There is no need to wait for the last test-taker to complete the test before item analysis can begin.- Item analysis should be conducted concurrently with test administration.- This validates not only that item selection and ability measurement are functioning correctly, but also that the items themselves are functioning at their specified difficulty levels.- Recent experience with the CAT version of the GRE, Graduate Record Examination (Smith, 1999) is a reminder that there must be a continuous program of quality control and test validation for CAT, just as much as for other testing methods.

 

A virtue of CAT is the new items can be introduced into the bank easily.- Initially, new items can be administered inconspicuously along with pre-existing items, but not used for test-taker ability estimation.- Instead, the test-takers' responses are used to verify the item is functioning as specified and to ascertain the item's precise difficulty.- Then the item can be made part of the regular bank.

 

When an item is revised it becomes a new item.- Revision must change some aspect of the item.- So it must impact the item's difficulty, or some other aspect of the item's functioning.- Consequently a revised item must be regarded as a new item, and its difficulty re-estimated accordingly.

 

CAT testing is often done at remote locations.- Under these circumstances, the item bank, even if encrypted and otherwise secured, should not be transported in its entirety to all locations.- Instead, different locations should be sent different, overlapping, sections of the item bank.- This has several benefits.- First, test security is improved because the theft of one test package does not compromise the entire bank.- Secondly, item exposure is limited.- Any item can only be seen by a fraction of the candidates, at most.- Thirdly, the chances of a large number of test-takers experiencing identical tests is diminished overall.-- Fourthly, if problems are discovered during test administration or afterwards, only a fraction of the CAT administrations is likely to be affected.- Fifthly, the overlap is introduced so that item difficulties at different sites can be compared and equated, thus insuring a fair evaluation of performance for all test-takers.

 

5. PRESENTING TEST ITEMS AND THE TEST-TAKER'S TESTING EXPERIENCE

 

Test items should be presented to test-takers as quickly, smoothly and clearly as possible.- Advances in computer technology are aiding this endeavor.- The rapid increase in Internet-based testing is a reflection of the ease with which test items can be formatted and presented using HTML or equivalent code.- In fact, a challenge to screen designers is to keep the design simple, without unnecessary distractions.- It is easy to put in "help" buttons, links and moving graphics, with the intention of assisting the test-taker to produce an optimum performance.- These features, however, may prove distracting, frustrating or time-consuming.- Just as new items must be field tested, so must CAT screen layouts and procedures.

 

High ability test-takers are sometimes perplexed by their experience of CAT.- Such test-takers are accustomed to 90%+ correct response rates on typical paper-and-pencil tests.- The success rate on a CAT test, however, is not determined by test-taker performance, but by the design of the item-selection algorithm.- If an optimum-targeting algorithm is employed, then the success rate for all test-takers, of whatever ability, to the items will be about 50% correct.- For high ability test-takers, such a low percentage of correct answers is a traumatic experience.- For any respondent who is easily discouraged this can provoke the feeling of "I've already failed".- Accordingly, testing agencies are suggesting that items be selected to give success rates of 60%, 70% or even 80% by test-takers across the items.- Consequently test-takers leave the CAT session, feeling that the test was challenging, but also that the test-taker was able to perform at an optimum level. This adjustment in success rate on the items is done by administering items to the test-takers about 1 logit less difficult than the test-takers are able.- This does increase the number of items that must be administered to obtain a given measurement precision, but only 10%-20%.

 

6. REPORTING RESULTS.

(A) TO THE TEST-TAKER.

 

CAT testing provides unusual opportunities to present immediate and useful feedback to both the test-takers and the testing agency.

 

At every point during the CAT administration of a test to a test-taker, the test-taker's current ability estimate is known.- The test-taker's success or failure on the previous item is also known.- Immediately at the conclusion of the administration of items, an entire diagnostic profile of the test-taker's performance can be constructed.

 

How much of all this information is to be communicated to the test-taker?

 

In high stakes, secure test situations, perhaps none of it.- It may be necessary to review all test performances, verify all scoring keys, and validate all other aspects of the test and its administration, before test reports are issued.- Under these circumstances, the less information is disseminated to test-takers, the fewer false hopes will be raised.

 

In classroom testing, however, feedback may encourage better performance.- CAT takes on the experience of a video game in which better performance is rewarded with higher scores.- Immediate feedback as to success on an item may reinforce learned material.

Immediate feedback on failure on an item may encourage the test-taker to take action to remedy the deficit.- Presenting to the test-taker a running report of the ability estimate may help overcome boredom, lack of motivation, or the impulse to complete the test as quickly as possible just by hammering the keys.

 

Here is one of the great contrasts between CAT and paper-and-pencil.- The report of the CAT test can unambiguously identify what has been mastered, what is in process of being learned, and what comprises the next higher strata of items to be attacked.- This enables both student and teacher to focus their efforts productively.- Studies in the Chicago Public Schools have indicated that the same material is taught over and over again, grade after grade to whole classrooms of students, because a few students in the classroom are deficient.- CAT would indicate immediately which few students need remedial attention, and what to focus on for the others.

 

6. REPORTING RESULTS.

(B) FOR TEST VALIDATION.

 

Summary item and test-taker statistics for CAT differ markedly from those for paper-and-pencil tests.- First, only a small proportion of the test-takers have been administered any particular item, so the proportion of missing responses may be 90% or more.- This renders classical item analysis useless.- Second, all items have been administered in such a way that the success rate on all of them is about 50% (or 60%, 70%, 80%, etc.).- Thus investigation of p-values is useless.- Third, nearly all items were administered to test-takers relatively on-target to them.- This means that there is almost no opportunity to witness patterns of obviously lucky guessing, and that even differences in item discrimination are hard to detect.

 

Item analysis and test validation, however, can proceed.- Despite high proportion of missing data, the items and test-takers do form an interconnected network.- When the items and persons are ordered according to difficulty and ability, then the scalogram (Guttman, 1944) of responses has the appearance of a sparse block-diagonal matrix.- This provides the basis for estimating item difficulties and test-taker abilities in a Rasch context.- The opportunity for distractor analysis, the investigation of the performance of incorrect MCQ options, is somewhat hampered by the uniform ability levels of test-takers exposed to each item.

 

Item and person fit analysis is somewhat subtle.- Conventional DIF (differential item function) analyses can be performed, but their impact is rather less than with paper-and-pencil tests.- CAT tends to be self-correcting.- DIF tends to make an item harder (or easier) than the bank difficulty value for a particular segment of test-takers.- Supposing that a test-taker fails such an item, then the CAT algorithm will administer an easier item.- The test-taker will succeed, and be given a harder item yet again, and be given another opportunity to perform at the higher level.- It has been argued that, in some tests, every item is biased against a particular segment of test-takers.- If so, then it is what the test is testing, rather than the individual items, that is problematic.

 

The most awkward form of item mis-performance, i.e., misfit to the Rasch model, for well-established items is item drift.- This is the change of item difficulty across time.- Sometimes the reasons for this are obvious, sometimes subtle, and sometimes inexplicable.- An obvious reason for item drift occurred for the item "Count backwards from ten to zero".- This used to be a difficult arithmetic item.- But once students became familiar with the launch sequence for rockets, this item was very easy.

 

Once the first good estimate of the difficulty of each item has been obtained, item re-estimation is almost always a matter of item drift.- If instructors attempt to teach to the test, or the text of particular items becomes common knowledge, then those items will become easier.- If a particular aspect of knowledge, skill or technique falls into disuse, then relevant items will become harder.- But usually the changes in item difficulty are small and unremarkable.

 

The focus of quality-control on test-taker performances is, do test-takers maintain their ability-levels throughout the test session?- It has been discovered (Gershon, 1992) that a few uncharacteristic incorrect responses on easy items at the start of a CAT session can be hard for a test-taker to overcome.- Linacre (1998) points out that, once a CAT test is well underway, even a run of continual successes only raises the test-taker's ability level slowly.- For instance, in a test of 260 items, success on the last 100 items only raises the test-taker's ability 1 logit. Accordingly, statistical test have been proposed that verify that the test-taker's ability level has remained essentially constant throughout the test.- These tests are similar to those that Shewhart proposed for industrial quality control (Shewhart, 1939).- van Krimpen-Stoop and Meijer (1999) report encouraging results with their variant of this approach, but its utility has yet to be determined in practice.

 

7. ADVANTAGES OF CAT.

 

Many of the advantages of CAT have been indicated in the preceding discussion, but they are collected here for reference purposes.

 

1. CAT avoids administering irrelevant questions.

Items that are much too easy or much too hard for test-takers provoke unwanted behavior, such as guessing, carelessness and response patterns.- These are largely eliminated.

 

2. CAT tests can be shorter.

It was originally thought that CAT administrations would have many fewer items than paper-and-pencil tests.- They are shorter, but not much.- In fact, in high stakes testing, they may be the same length!- Optimally, a CAT test stops when a pass-fail decision has been reached.- This is usually made when

 

3. CAT tests can be quicker to develop, implement and report.

For classroom level tests, the test is ready to go as soon as the items are typed in.- The reporting is immediate, and their is no test grading to be done at home afterwards!- For high stakes tests, the error-prone collection, scanning, scoring and reporting of OMR bubble-sheet forms is avoided.

 

4. A mis-keyed item will have hardly any impact on test results.

Every year, it seems, a flaw is discovered in the scoring key of a high-stakes test, requiring the recall of pass-fail notifications.- With CAT, a miskeyed item would only affect a segment of the test-takers, and even for those, the self-correcting nature of CAT would make it unlikely there would be any impact on the pass-fail decision.

 

5. CAT tests can be better experiences.

Here is how Craig Deville (1993) expresses it:

"In our studies, we found that every flow activity... provides a sense of discovery, a creative feeling of transporting the person into a new reality." (Mihaly Csikszenmihalyi, The Psychology of Optimal Experience, Harper & Row, 1990 p.74)

 

Csikszenmihalyi describes how human activities often comprise two opposing components, which, in the Diagram (in printed text) are characterized as Challenges and Skills. So long as the level of challenge facing the player of a game is in rough accord with the level of the player's skill, then the player will experience a "sense of discovery", or even a "previously undreamed-of state of consciousness" - that is flow. But as the player's skill increases, the player will grow bored. Or when the challenge of the game increases too far beyond the player's skill, frustration will set in. Both boredom and frustration inhibit the flow experience. The motivation towards enjoyment provokes one to desire to balance challenge with skill, and so to induce flow.

 

Tailored testing can take advantage of the phenomenon of flow to make the testing experience pleasurable and to improve individual performance. Well-targeted items will make the testing situation less irksome, perhaps even enjoyable! Targeting removes items that are too hard, so inducing anxiety, and those that are too easy, so inducing boredom. Psychometrically, the better the match between the item's difficulty and the test-taker's ability, the greater the likelihood that the situation will produce accurate measures. After a test that successfully matches item difficulties with test-taker ability, test- takers can leave feeling content that their optimum performance levels have been demonstrated, and test constructors can count on accurate measures. A flow experience for all!

 

Rudner's Advantages

 

Here are the advantages identified by Rudner (1998) :

 

1. In general, computerized testing greatly increases the flexibility of test management, e.g. Urry, 1977; Grist, Rudner, and Wise, 1989; Kreitzberg, Stocking, and Swanson, 1978; Olsen, Maynes, Slawson and Ho, 1989; Weiss and Kingsbury, 1984; Green, 1983).

 

2. Tests are given "on demand" and scores are available immediately.

 

3. Neither answer sheets nor trained test administrators are needed. Test administrator differences are eliminated as a factor in measurement error.

However, supervision is still needed, and the environment in which CAT is conducted can definitely affect test results.

 

4. Tests are individually paced so that a examinee does not have to wait for others to finish before going on to the next section. Self-paced administration also offers extra time for examinees who need it, potentially reducing one source of test anxiety.

 

5. Test security may be increased because hard copy test booklets are never compromised.

Further, if no two people take the same test, parroting answers or copying from someone else is pointless.

 

6. Computerized testing offers a number of options for timing and formatting. Therefore it has the potential to accommodate a wider range of item types.

These can include moving images, sounds, and items that change their appearance based on responses to previous items.

 

7. Significantly less time is needed to administer CATs than fixed-item tests since fewer items are needed to achieve acceptable accuracy. CATs can reduce testing time by more than 50% while maintaining the same level of reliability.

A drop as great at 50% must mean that the paper-and-pencil test was conspicuously too easy or too hard.- Reliability is an awkward term to use for CAT testing, because, for fixed length tests it is based on the standard deviation of the sample ability estimates and the average standard error of those estimates.- In individually-administered CAT tests, the idea of a sample becomes more diffuse.- Consequently, the comparison, in practice, is not expressed in terms of test reliabilities, but in terms of measure standard errors.

 

8. Shorter testing times also reduce fatigue, a factor that can significantly affect an examinee's test results.

 

9. CATs can provide accurate scores [measures] over a wide range of abilities while traditional tests are usually most accurate for average examinees.

8. CAUTIONS WITH CAT.

 

Fairtest's Problems

 

According to Fairtest (1992?), here is a list of what they claim to be unresolved problems with CAT.

 

1. "Test-makers claims that the scores of computerized and pencil-and-paper tests are equivalent are inadequately supported. In fact, research studies find there usually is a difference. Most studies show higher scores for paper-and-pencil exams, but a few have found advantages for those who take computerized tests. These averages may mask individual variations. Some respondents may still get lower scores even if the average score increases. Also, some types of questions perform differently on the two types of tests." (Bugbee and Bernt, 1990)

 

It is not the "score on the test", but the ability estimate of the test-taker that is critical.- Some questions do indeed perform differently on the two types of test.- The question is not "which gives a higher score", but "which gives a better estimate of ability".- Asking on-target questions, as in CAT, must surely give a better indication of test-taker ability than administering items that are obviously too hard or too easy for any particular test-taker as paper-and-pencil tests tend to do.

 

2. Computerized tests constrain test-takers compared to paper-and-pencil tests. With computerized versions, test-takers are unable to underline text, scratch out eliminated choices and work out math problems -- all commonly-used strategies. Studies also suggest that computer screens take longer to read than printed materials, and that it is more difficult to detect errors on computer screens. (Bugbee and Bernt, 1990)

 

3. Most computerized tests show only one item on the screen at a time, preventing test-takers from easily checking previous items and the pattern of their responses, two other practices known to help test-takers. Scrolling through multiple screens does not allow side-by-side comparisons.

 

4. Test-takers with the ability to manipulate computer keys rapidly may be favored by long passages that require reading through many screens.

 

These are genuine criticisms and are motivating improved item presentation methods.- Paper-and-pencil tests also have their design flaws, such as the ease with which answers are misaligned on OMR bubble-sheets, but most students have learned to live with them.

 

5. Test-makers may try to use computerized exams to circumvent Truth-in-Testing disclosure requirements. ETS has not revealed how it intends to continue making test questions and answers available to university admissions test-takers.

 

In fact, it is easier to make questions available when item banks are used, because items are entering and leaving the bank continually.- Those leaving the bank can be released to the public.

 

6. Computers may worsen test bias. The performance gap which already exists on multiple-choice tests between men and women, ethnic groups, and persons from different socioeconomic backgrounds could widen as a result of computerized testing.

 

7. Schools with large minority or low-income populations are far less likely to have computers, and poor and minority children are much less likely to have computers at home (Sutton, 1991; Urban, 1986). White students are more likely to have earned computer science credit than either African American or Hispanic students (Urban, 1986).

 

8. Girls may be adversely affected by computerized tests. A much greater number of females than males report no school access to computers, no computer learning experiences, and limited knowledge about computers (Urban, 1986). In addition, computer anxiety is much more prevalent among females than males (Moe and Johnson, 1988), with Black females reporting the greatest anxiety (Legg and Buhr, 1992).

 

This was written when computers were a comparative novelty.- As computer technology becomes ever more commonplace in society, computers may well lessen test bias!- An analogy could be drawn with cellular phones and pagers, which are now used by all levels of society in the USA, removing the source of bias that one must have a fixed place of residence to have a telephone.- Advances in computer technology are removing literacy barriers in a similar way.

 

8. The additional cost of computerized tests is certain to have a large effect on who chooses to take them. Poorer students are unlikely to take the computerized GRE, for example, because it costs nearly twice as much as the paper-and-pencil version.

 

This seems to contradict Fairtest's first objection!- Why would rich students deliberately choose a test format with which they would perform less well?- In fact, there are many economies associated with CAT, such as flexibility in test scheduling, which mean that ultimately CAT will be, if it is not already, less expensive for both test agencies and test-takers.

 

Rudner's Limitations

 

Here are the limitations to CAT identified in Rudner (1998).

 

1. CATs are not applicable for all subjects and skills. Most CATs are based on an item-response theory model, yet item response theory is not applicable to all skills and item types.

 

This is true. Similar limitations apply to paper-and-pencil tests.

 

2. Hardware limitations may restrict the types of items that can be administered by computer. Items involving detailed art work and graphs or extensive reading passages, for example, may be hard to present.

Advances in computer technology and better item presentation are eliminating many of these concerns.

 

3. CATs require careful item calibration. The item parameters used in a paper and pencil testing may not hold with a computer adaptive test.

As Wright and Douglas (1975) and other studies show, there is no for exact item calibration.- Neither is there a need for the estimated difficulty of CAT items to exactly match the paper-and-pencil estimated difficulties.- In fact, because of the more relevant sample, the CAT item difficulties should be more believable.

 

4. CATs are only manageable if a facility has enough computers for a large number of examinees and the examinees are at least partially computer-literate. This can be a big limitation.

The extent of this limitation depends on the reason for the test and the characteristics of the test-takers.- Classroom level CAT can be done on one computer by one child at a time.- Low stakes tests can be done via the Internet.- Rudner is here referring to large-scale tests such as the SAT and ACT.- These are already under more powerful attack for other reasons.

 

5. The test administration procedures are different. This may cause problems for some examinees.

As computers become more pervasive, it may be the paper-and-pencil tests, with their bubble sheets, that are seen as problematic.

 

6. With each examinee receiving a different set of questions, there can be perceived inequities.

This is why it is essential that every test-taker be administered enough items to insure that their final ability estimate is unassailably reasonable.

 

7. Examinees are not usually permitted to go back and change answers.

Improved item selection and ability estimation algorithms now allow test-takers to review and change previous responses.

 

8. [If changing responses is permitted,] A clever examinee could intentionally miss initial questions. The CAT program would then assume low ability and select a series of easy questions. The examinee could then go back and change the answers, getting them all right. The result could be a 100% correct answers which would result in the examinee's estimated ability being the highest ability level.

This has been investigated both in practice and statistically, and found to be a wild gamble.- It based on the incorrect notion that a perfect score on an easy test will result in an ability estimate at the highest level.- In fact, with effective CAT algorithms, such as those of Halkitis or UCAT, it will not.

 

Gershon and Bergstrom (1995) considered this strategy under the best possible conditions for the potential cheater: a CAT test which allows an examinee to review and change any responses. This type of examinee-friendly CAT is already used in high-stakes tests and will rapidly spread, once CAT fairness becomes a priority.

 

Consider an extreme case in which an examinee deliberately fails all 30 items of a 30 item CAT test. After these 30 items, the algorithm would assign that examinee a minimum measure. But then, at the last moment, the examinee reviews all 30 items, most of which are very easy, and corrects all the responses. What happens?

 

 

Figure 10 depicting obtained versus real ability shows the answer. When real ability is high, all items will end up correct. But they are easy items, so the obtained ability will not be so high. Cheaters with high real abilities will invariably lose. It turns out that, at best, lower ability cheaters can obtain no more than an extra .2 logits beyond their real ability. Usually even these cheaters lose because, if they make just one slip, their obtained ability will be lower than their real ability. And now there may no longer be the opportunity to take more items to recover from that mistake, as there would be during normal CAT test administration. Should cheaters accidently exit without making corrections, they could lose 8 or more logits.

 

Under the most favorable circumstances this strategy can only help the examinee minutely, and even that at the risk of disaster.

 

A word to wise examinees: Do not attempt this method of cheating!

 

The Results of a Study into Adaptive Testing

 

Wouter Schoonman's An applied study on computerized adaptive testing (Rockland MA: Swets & Zeitlinger, 1989) is a treasury of useful CAT information for the discerning, but occasionally skeptical, reader.- Schoonman's aim was to construct a CAT system for the Dutch version of the General Aptitude Test Battery (GATB).- For this endeavor, he perused the literature (providing a comprehensive reference list) and consulted the best minds in The Netherlands.- Naturally, he encountered the usual CAT dragons.- He found that many specialists favor fitting elaborate psychometric models to their responses.- Nevertheless, the exigencies of missing data, small sample sizes and the need to construct a useful item bank forced him to conclude that Aadvantages outweigh the disadvantages in favor of the use of the [Rasch] model.@

 

His choice of an item selection algorithm was dominated by the customary superstitions: 1) accurate measurement requires precise item pre-calibration, 2) all the benefits of CAT ride on managing to administer the absolute minimum number of items, and 3) the CAT algorithm must be complicated to be good.- Fortunately, the description Schoonman gives of his complicated Bayesian algorithm is sufficiently opaque to inhibit others from trying to copy this part of his work.- The main benefit claimed for his Bayesian algorithm is that it produces uniform measurement error.- But a stop rule based on the standard error of measurement, which does just that, can be implemented with the simplest estimation algorithm given above.

 

Schoonman uses three personality inventories to investigate examinees' attitudes to computers and test-taking behavior.- He did not detect any strong interactions between personality traits and test results.- Schoonman also discusses the practical problem of converting GATB (General Aptitude Test Battery) items from their speeded written form to the power-oriented computer-administered form.- He discovered that, when the written version is administered to an examinee first and immediately followed by the CAT version, then speeded test-taking strategies are used by the examinee for the CAT power test.- The result is a CAT score lower than expected.- This provokes an investigation into response time and the discovery that, for the GATB, it is inversely correlated with ability.

 

Schoonman's experiences match those of many other attempts to implement CAT.- An essentially simple and straightforward process is made cryptic and complicated.- An advantage of CAT is that its success can be verified and amended at every point without detriment to prior work.- Items can be written, screen layouts designed, selection algorithms written, estimation algorithms improved, report forms conceptualized, item banks produced, all as independent and parallel processes.- Even once test administration has begun, fine tuning of item selection algorithms, report formats, and item exposure can be performed.

 

There are hazards in CAT. Many are obvious. These include lack of familiarity with the computer by test-takers, lack of proper monitoring of the test administration, lack of security of the test material.

 

A more subtle problem is that of item over-exposure or over-use, leading to test "tracking".- Many theoretical discussions of CAT imagine the item bank to contain infinitely many items, uniformly distributed.- In practice, however, items are unevenly lumped along the variable.- Figure 11 shows a typical case of item over-use.- The items, A-H, are the only 8 items in the item bank on this part of the measurement variable.- During the test session, the estimated abilities of 8 different test-takers were instantaneously also located in this same part of the variable.

 

Which items should they be administered?

 

According to Schoonman (1989) and many other CAT theoreticians, the item that gives the maximum statistical information about their performances.- In Figure 11, those items are the ones nearest to the test-takers' ability estimates.- Thus Test-taker 1 is administered Item B, Test-takers 2, 3, 4 are administered Item D, Test-takers 5, 6, 7 are administered Item E, and Test-taker 8 is administered Item H.- It is seen that Items D and E are over-used, but items A, C, F, G are never used!- Worse, if two Test-takers are administered the same item, and they both succeed or fail, then it is likely that they will be administered the same next item.- This is called "test tracking", and leads to both a series of over-used items, and a group of test-takers experiencing the same test.

 

 

 

This type of item over-exposure and test tracking occurs whenever a deterministic item selection rule is used that does not explicitly guard against these phenomena.- The easiest safeguard to implement is that of local randomization.- This is used in UCAT.- Instead of choosing the maximally informative item, an item is chosen at random from a maximally informative region.- In UCAT, this is the region between the current high and low estimates of test-taker ability.- The information function for a standard dichotomous item is shown in Figure 12.- This shows that any item within "0.6 logits of the test-taker ability function is contributing 90% or more of the maximum possible information, assuming that an item so perfectly targeted on the test-taker exists in the item bank, and has not been previously administered to the test-taker.

 

Another method of controlling item over-exposure is to keep track of how many times each item has been used, and equalize their use.- On a large scale, this requires considerable data gathering effort and communication between test sites.- It can certainly be easily done, however, at each individual testing station for that testing station.

 

REFERENCES

 

Adams, R.J. (1988) Applying the partial credit model to educational diagnosis. Applied Measurement in Education 1(4): 347-361

 

Alderson, J.C., and North, B. (Eds) (1991) Language Testing in the 1990s: The Communicative Legacy. MacMillan Publishers, London

 

Andrich, D.A. (1990) The ability of an item. Rasch Measurement Transactions 4:2, p. 101.

 

Baker, F.B. (1986) Item banking in computer-based instructional systems. Applied Psychological Measurement 10(4): 405‑414

 

Baker, F.B. (1992) Item response theory: parameter estimation techniques. Dekker, New York.

 

Binet, A., Simon, and Th. (1905) Méthodes nouvelles pour le diagnostic du niveau intellectual des anormaux. Année psychol., 1905, 11, 191-244.

 

Bosma J.F. (1985) Teacher and Student Responses to a System for Rational Measurement. Chicago: University of Chicago. Ph.D. Dissertation.

 

Bradlow, E. T., Weiss, R. E., and Cho, M. (1998). Bayesian identification of outliers in computerized adaptive tests. Journal of the American Statistical Association, 93, 910‑919.

 

Brown, J.D., (1997) Computers in language testing: present research and some future directions. Language Learning & Technology. 1:1, 44-59

 

Bugbee, A.C. and Bernt, F.M. (1990) Testing By Computer: Findings in Six Years of Use 1982-1988, Journal of Research on Computing in Education (Vol. 23, #1, pp. 87-100, 1990).

 

Cohen, L. (1979) Approximate expressions for parameter estimates in the Rasch model. British Journal of Mathematical and Statistical Psychology 32(1): 113‑120

 

Csikszenmihalyi, M. (1990) The Psychology of Optimal Experience, Harper & Row.

 

Davey, T., Pommerich, M., and Thompson, T.D. (1999) Pretesting alongside an operational CAT. Paper presented at the Annual Meeting of the National Council of Measurement in Education, Montreal, Canada.

 

Deville, C. (1993) Flow as a testing ideal. Rasch Measurement Transactions 7:3, p. 308.

 

Drasgow, E, Levine, M. V, and Williams, E. A. (1985). Appropriateness measurement with polychotomous item response models and standardized indices. British Journal of Mathematical and Statistical Psychology, 38, 67‑86.

 

Du, Y., et al. (1993) Computerized Mastery Testing Using Fuzzy Set Decision Theory. Applied Measurement in Education, 6:3, 181-93.

 

Eurocentres Learning Service (1991) CALL Computer Assisted Language Learning Authoring Program. Author, Zurich, Switzerland

 

Fairtest (1992?) Computerized Testing: More Questions than Answers. Cambridge MA: The National Center for Fair and Open Testing.

 

Gan‑Ng A.‑C. (1984) The statistical properties of an algorithm for classroom tailored testing. Chicago: University of Chicago. M.A. Paper.

 

Gershon, R.C. (1992) Test Anxiety and Item Order: New Concerns for Item Response Theory. Chapter 11 in M Wilson (Ed.) Objective Measurement: Theory into Practice. Vol. 1. Ablex, Norwood NJ

 

Gershon, R.C., and Bergstrom, B. (1995) Does cheating on CAT pay: NOT!. Paper presented at MOMS. Chicago.

 

Guttman, L. (1944) A basis for scaling qualitative data. American Sociological Review, 9:2, p.139

 

Halkitis, P.N. (1993) A computer-adaptive testing algorithm. Rasch Measurement Transactions 6:4, 254-5.

 

Hambleton, R. K. and Swaminathan, H. (1985) Item Response Theory: principles and applications. Kluwer‑Nijhoff, Boston.

 

Henning, G. (1987) A guide to language testing. Cambridge, Mass.: Newbury House

 

Legg, S.M. & Buhr, D.C. (1992) Computerized Adaptive Testing with Different Groups, Educational Measurement: Issues and Practice. Summer. pp. 23-7.

 

Levine, M.V., and Drasgow, E. (1988) Optimal appropriateness measurement. Psychometrika, 53, 161‑176.

 

Levine, M.V., and Rubin, D.B. (1979) Measuring the appropriateness of multiple‑choice test scores. Journal of Educational Statistics, 4, 269‑290.

 

Linacre J.M. (1987) Computer-adaptive testing - How many questions are enough. Paper presented at American Educational Research Association (AERA) Annual meeting, Washington DC. April 20.

 

Linacre J.M. (1987) UCAT: a BASIC computer-adaptive testing program. MESA Memorandum number 40, MESA Psychometric Laboratory, University of Chicago. (ERIC ED 280 895)

 

Linacre J.M. (1988) Computer-adaptive testing: Simple and effective algorithms. Paper presented at AERA Annual Meeting. New Orleans. (ERIC ED 294 918)

 

Linacre J.M. (1990) Computer-adaptive testing in the classroom. In J. Keeves (Ed.) The International Encyclopedia of Education: Supplementary Volume Two. Oxford: Pergamon Press.

 

Linacre J.M. (1990) Uncomplicated Computer-Adaptive Testing, Computer Program EDN0030, abstracted in Zenith Data Systems, Masters of Innovation II.

 

Linacre J.M. (1995) CAT: A Bayesian approach. Rasch Measurement Transactions 9:1, 412-3.

 

Linacre J.M. (1996) Practical Computer-adaptive Testing. Presented at CARLA Conference. February. Minneapolis.

 

Linacre J.M. (1998) CAT: Maximum possible ability. Rasch Measurement Transactions 12:3, 657-8.

 

Linacre J.M. (1999) A measurement approach to computer-adaptive testing of reading comprehension. Chapter 10 in M. Chalhoub-Devine (Ed.) Issues in computer-adaptive testing of reading proficiency. Cambridge: University of Cambridge Local Examinations Syndicate.

 

Linacre, J.M., and Wright, B.D. (1988) BIGSTEPS Rasch Measurement Computer Program. Chicago: MESA Press.

 

Lunz M.E., Bergstrom B.A., Wright B.D. (1992) The effect of review on student ability and test efficiency for computerized adaptive tests. Applied Psychological Measurement 16(1): 33-40

 

Masters, G., Lokan, J., Doig, B., Toon, K.S., Lindsey, J., Robinson, L., Zammit, S. (1990) Profiles of Learning. Australian Council for Educational Research, Hawthorn, Australia

 

McBride, J.R., Martin, J.T. (1983) Reliability and Validity of Adaptive Ability Tests in a military setting. in Weiss D.J. (Ed.) "New Horizons in Testing" New York: Academic Press

 

McLeod, L. D. and Lewis, C. (1998). A Bayesian approach to detection of item preknowledge in a CAT. Paper presented at the Annual Meeting of the National Council of Measurement in Education, San Diego, CA.

 

Meijer, R.R., Molenaar, I.W, and Sijtsma, K. (1994). Item, test, person and group characteristics and their influence on nonparametric appropriateness measurement. Applied Psychological Measurement, 18, 111‑120.

 

Moe, K.C. & Johnson, M.F. (1988) Participants Reactions to Computerized Testing, Journal of Educational Computing Research, 4:1, 79-86.

 

Molenaar, I.W and Hoijtink, H. (1990) The many null distributions of person fit indices. Psychometrika, 55, 75‑106.

 

Molenaar, I.W and Hoijtink, H. (1996) Person fit and the Rasch model, with an application of knowledge of logical quantors. Applied Measurement in Education, 9, 27‑45.

 

Nering, M.L. (1997) The distribution of indexes of person fit within the computerized adaptive testing environment. Applied Psychological Measurement, 21, 115‑127.

 

Nitko, A.J., Hsu, T.-C. (1984) A comprehensive microcomputer testing system for classroom testing. Journal of Educational Measurement 21(4): 377‑390

 

Page, E.S. (1954) Continuous inspection schemes. Biometrika, 41, 100‑115.

 

Rasch, G. (1960/1992) Probabilistic Models for Some Intelligence and Attainment Tests. Copenhagen and Chicago: MESA Press.

 

Reckase, M.D. (1974) An interactive computer program for tailored testing based on the one-parameter logistic model. Behavior Research Methods and Instrumentation 6(2): 208‑212

 

Reise, S.E. (1995) Scoring method and the detection of person misfit in a personality assessment context. Applied Psychological Measurement, 19, 213‑229.

 

Reise, S.E. and Due, A.M. (1991) The influence of test characteristics on the detection of aberrant response patterns. Applied Psychological Measurement, 15, 217‑226.

 

Roskam, E.E. and Jansen, P.G.W. (1984) A new derivation of the Rasch model. p. 293-307 in E. Degreef & J. van Buggenhaut (Eds), Trends in Mathematical Psychology. Amsterdam: North-Holland.

 

Rudner, L. (1998) An On-line, Interactive, Computer Adaptive Testing Mini-Tutorial. ERIC Clearinghouse on Assessment and Evaluation.

 

Schoonman, W. (1989) An applied study on computerized adaptive testing. Rockland, MA: Swets & Zeitlinger.

 

Shewhart, W.A. (1939) Statistical Method from the Viewpoint of Quality Control. Washington: Dept. of Agriculture.

 

Siegmund, D. (1985) Sequential Analysis: Tests and Confidence Intervals. Springer‑Verlag, New York.

 

Smith, G. (1999) No more No. 2 pencil. ABC Internet News.

 

Snijders, T. (1999) Asymptotic distribution of person‑fit statistics with estimated person parameter. Psychometrika.

 

Stevenson J. (1987) Computerized Adaptive Testing in the Montgomery County, Maryland Public Schools. St. Paul, MN: Assessment Systems Corporation: MicroCAT News April 1987.

 

Sutton, R. (1991) Equity and Computers in the Schools: A Decade of Research, Review of Educational Research. 61:4, 475-503.

 

Urban, C.M. (1986) Inequities in Computer Education Due to Gender, Race, and Socioeconomic Status. Exit Project, Indiana University.

 

Vale C.D., and Giaculla, K.A. (1988) Evaluation of the efficiency of item calibration. Applied Psychological Measurement 12 53-67.

 

Vale C.D., and Weiss, D.J. (1987) MicroCAT Testing System. Assessment Systems Corporation, St. Paul, Minnesota

 

van der Linden, W.J. (1999) Multidimensional adaptive testing with a minimum error-variance criterion. Journal of Educational and Behavioral Statistics. 24:4, 398-412.

 

van Krimpen-Stoop, E.M.L.A., and Meijer, R.R. (1999) CUSUM-Based Person-Fit Statistics for Adaptive Testing. Research Report 99-05. University of Twente. Educational Measurement and Data Analysis.

 

Warm, T.A. (1989). Weighted likelihood estimation of ability in item response theory. Psychometrika, 54.

 

Weiss, D.J. (1983) Introduction in Weiss D.J. (Ed.) "New Horizons in Testing" New York: Academic Press

 

Weiss, D.J., and Kingsbury, G.G. (1984) Application of computerized adaptive testing to educational problems. Journal of Educational Measurement, 21:4 361-375

 

Wright, B.D. (1987) Testing to a Standard. Chicago: University of Chicago, MESA

 

Wright, B.D. (1988) Practical adaptive testing. Rasch Measurement Transactions 2(2): 21

 

Wright, B.D. (1988) Rasch model from Campbell Concatenation. Rasch Measurement Transactions 2:1, p.16.

 

Wright, B.D. and Bell, S.R. (1984) Item banks: what, why, how. Journal of Educational Measurement 21: 331‑345

 

Wright, B.D. and Douglas, G. (1975) Best test design and self-tailored testing. MESA Memorandum No. 19. Department of Education, Univ. of Chicago

 

Wright, B.D. and Masters, G.N., (1982) Rating Scale Analysis: Rasch Measurement. Chicago: Mesa Press

 

Wright, B.D. and Panchapakesan, N. (1969) A procedure for sample-free item analysis. Educational & Psychological Measurement 29 1 23-48

 

Wright, B.D. and Stone, M.H. (1979). Best test design. Mesa Press, Chicago.

 

Yao, T. (1991) CAT with a poorly calibrated item bank. Rasch Measurement Transactions 5:2, p. 141.

 

Appendix: The UCAT computer-adaptive testing program.

 

Program 1: The UCAT.BAS CAT Administration and Bank Recalibration Program

 

'$DYNAMIC

'- Computer‑adaptive test presentation and scoring program

'- Written by John Michael Linacre 1986 ‑ modify freely

'

' UCAT Control Options

'/D-------- go into debug mode ‑ display item difficulties and answers

'------ ----while item is administered.

'

'/Annn----- set standard error of final estimate (i.e. length of test)

'---------- in local units

'

'/S-------- means supervisor conducts test ‑ reports scores to screen

'---------- and allows item bank recalibration

'

'/Ifilename provide name of item bank of test questions

'---------- e.g. /Imathbank

'---------- if appended by ".SEC" then itembank is in secure format:

'---------- /Imathbank.sec

'

'/Pfilename provide name of data file for person responses

'---------- e.g. /Pstudent

'---------- if appended by ".SEC" then person data is in secure format:

'---------- /Pstudent.sec

'

'e.g. to give a standard secure CAT test without a supervisor,

'---- but with a S.E. of .5 logits = 4.5 CHIP units:

'

'C:>UCAT /Iitembank.sec /Pdata.sec /A4.5

'

'Security:

'

'The program "SECURE" converts between secured ".SEC" and non‑secured files.-

'- Put this on your diskette but not on the students!

'

'At DOS prompt:

'

'c:>SECURE itembank

'---------- write secured file "itembank.sec" from file "itembank"

'

'c:>SECURE itembank.sec

'---------- write unsecured file "itembank" from file "itembank.sec"

'

'------------ Explanation of BASIC variable names

'Variable------ Description

'‑‑‑‑‑‑‑‑------ ‑‑‑‑‑‑‑‑‑‑‑

'ABILITY------- Estimate of ability, sometimes assumes next answer wrong

'ABILRIGHT----- Estimate of ability, if next answer right

'ACCURACY------ Maximum width of likely zone of estimate, =2*standard error

'ANSWERS$------ Valid responses to questions:

'---------------- Update the list if responses not "12345"

'BIAS---------- Adjustment for statistical bias

'CURSCOL%------ Current cursor column on screen

'CURSROW%------ Current cursor row on screen

'FNL----------- Function to convert external units to logits (‑10 to +10)

'FNU----------- Function to convert logits to external units (1‑200)

'I------------- Subscript index and numerical working variable

'KEYSTR$------- Last key pressed

'L------------- Subscript index and numerical working variable

'MAXITEMS------ Number of questions in item file (calculated by program)

'MAXPERSONS---- Maximum number of persons to re‑estimate (set by user)

'MSG$---------- Message to be sent to screen

'N------------- Numerical working variable

'NAM$---------- Name of test taker

'P------------- Current location in test‑taker array

'PABILITY()---- Estimated test‑takers' abilities

'PADJ---------- Total of previous ability estimates

'PANSWER()----- Answers keyed in by test‑taker to questions asked

'PASKED-------- Number of questions asked or number of answers to a question

'PEXP---------- Expected score by test‑taker

'PQUESTION()--- Location in QTEXT$ array of questions asked test‑taker

'PRESULT------- Count of questions asked a test‑taker

'PSCORE()------ Count of test‑taker's correct answers, i.e. raw score

'PSE()--------- Standard error of estimation (accuracy) of ability estimates

'PSUM---------- Sum of all ability estimates

'PTOTAL-------- Total number of test‑takers being reestimated

'PVAR---------- Variance of expected score for a test‑taker

'Q------------- Location in question arrays

'QASKED()---- Number of times question has been asked

'QCOUNT-------- Number of questions in question file

'QDIFF()------- Difficulty estimates for questions

'QEXP()-------- Estimated score based on ability and difficulty estimates

'QFIL$- --------Name of question text file

'QSCORE()------ Count of number of correct answers to each question

'QSELECT------- Location of next question to be displayed in question array

'QTEXT$(,10)--- Text of questions and answer options (10 lines per question)

'QTOTAL-------- Total number of questions being reestimated

'QVAR()-------- Variance of expected score by test‑taker's on a question

'RECOUNT------- Working variable to control recounting and reestimating

'RESIDUAL------ Difference between actual and estimated scores

'RESPONSE$----- Response to the question

'RESULT%(,)---- Answers by test‑takers to questions:--

'----------------- 1=correct 0=incorrect ‑1=unknown (not taken)

'SE------------ Standard error of estimation of ability measure

'SUCCESS------- Probability of correct answer by test‑taker to question

'TEXT$--------- Text data

'TFIL$--------- Name of file of test‑taker's abilities and responses

'TREVFIL$------ Name of revised test‑taker file

'VALID$-------- Valid responses for for pressed keys

'

' Arrays are dimensioned for MAXPERSONS=500 test‑takers.

'

' Modify this code for your own Logit to Reporting Unit Conversion

' Currently, external units are set at 10 units = 1 logit

' External units=(logits*10) ... logits=(external units*0.1)

 

10 'Conversion between logits and user's measurement units

- DEF FNU (i) = CINT(i * 10) : DEF FNL (TEXT$) = VAL(TEXT$) * .1

 

' End of reporting unit modification

 

' Mainline of code: check command line switches.

' this program can be invoked with command line switches.

' COMMANDLINE$=COMMAND$

' if the line above is not supported, you cannot use DOS command line prompts

' enter your prompt here:

20 ' UCAT program control options

- INPUT "COMMAND OPTIONS (/D /S FOR FULL DISPLAY) OR PRESS ENTER KEY: ",_

------- COMMANDLINE$

 

- IF INSTR(UCASE$(COMMANDLINE$), "/D") > 0 THEN debug% = ‑1 'Debug information

- i% = INSTR(UCASE$(COMMANDLINE$), "/A")' set accuracy limit

- IF i% > 0 THEN

---- ACCURACY = FNL(MID$(COMMANDLINE$, i% + 2))

- ELSE

---- ACCURACY = .7- 'measure ability within zone of .7 LOGITS

- END IF

- IF INSTR(UCASE$(COMMANDLINE$), "/S") > 0 THEN super% = ‑1 '/S supervisor mode

- '------------------------------- prints number of items in bank

- i% = INSTR(UCASE$(COMMANDLINE$), "/I")'item bank

- IF i% > 0 THEN

----- j% = INSTR(i%, UCASE$(COMMANDLINE$) + " ", " ")

----- QFIL$ = MID$(COMMANDLINE$, i% + 2, j% ‑ i% ‑ 2)

- END IF

- i% = INSTR(UCASE$(COMMANDLINE$), "/P")'person file

- IF i% > 0 THEN

----- j% = INSTR(i%, UCASE$(COMMANDLINE$) + " ", " ")

----- tfil$ = MID$(COMMANDLINE$, i% + 2, j% ‑ i% ‑ 2)

- END IF

 

30 ' Initialize

- MAXPERSONS = 500 'Update to reflect maximum number of persons

- RANDOMIZE TIMER- 'set random number generator so it differs every time

- CLS : PRINT "Preparing to administer test questions .."

40 ' Obtain the name of the question file

- IF QFIL$ = "" THEN

---- INPUT "What is the name of your pre‑existing file of questions"; QFIL$

- ENDIF

50 ' Verify the question file

- GOSUB 850 'Find how many options AND HOW MANY ITEMS

60 ' Report number of items and options

- IF super% THEN

---- PRINT "There are" + STR$(maxitems) + " items in the bank, with"_

------- + STR$(maxanswer%) + " options each"

- ENDIF

70 ' Establish the item and person arrays in memory

- DIM QASKED(maxitems), QDIFF(maxitems), QEXP(maxitems), QSCORE(maxitems)

- DIM QTEXT$(maxitems, MEASURE%), QVAR(maxitems), result%(MAXPERSONS, maxitems)

- IF maxitems > MAXPERSONS THEN MAXPERSONS = maxitems'TO ALLOW ENOUGH ROOM

- DIM PABILITY(MAXPERSONS), PANSWER(MAXPERSONS), PQUESTION(MAXPERSONS)

- DIM PSCORE(MAXPERSONS), PSE(MAXPERSONS)

80 ' Input the question text

- GOSUB 870 'Read in the questions

90 ' Identify output file

- IF tfil$ = "" THEN

----- INPUT "What is the name of your output file of test‑takers"; tfil$

- ENDIF

120- 'Test administration begins

--IF super% THEN MSG$ = "Do you want to give a test?": GOSUB 810

- IF (RESPONSE$ = "Y") OR NOT super% THEN

------- GOSUB 180: GOSUB 2660 'administer test and write results

------- IF super% GOTO 120'Administer another- test

- END IF

130 ' Reestimate item difficulties

- IF super% THEN

--- MSG$ = "Do you want the computer to reestimate question difficulties?"

--- GOSUB 810: IF RESPONSE$ = "Y" THEN GOSUB 960: GOTO 120'reestimate

--- PRINT "Then we have finished. Review the responses in file " + tfil$

- END IF

--WHILE LEN(INKEY$) > 0: WEND

- PRINT "Thank you! ‑ Please press any key to conclude test session"

- WHILE LEN(INKEY$) = 0: WEND

- SYSTEM

' UCAT concludes.

 

180 ' Conduct a test session

- CLS : PRINT "Welcome to a Computer‑administered test session!": PRINT

- INPUT "Please type your name here:", nam$

200 ' Establish initial ability

- ABILITY = qmean ‑ (.5 + .5 * RND) 'Starting ability is between 90 and 95

- ABILRIGHT = ABILITY + 1: SE = ACCURACY'Upper ability estimate 100‑105

220 ' Flag questions as unasked

- FOR Q = 1 TO qcount: QASKED(Q) = 0: NEXT Q '0 means question not asked

- PASKED = 0: presult = 0

230 ' select first question

- GOSUB 460'select starting question

240 ' ask question and update ablity estimates

- WHILE QSELECT <> 0: GOSUB 330

250 ' select next question, then read answer to this one!

- GOSUB 460: GOSUB 540: WEND'choose next question, check previous answer

--- ' test is finished

- IF PASKED = 0 THEN RETURN' no questions asked

270- ' Do another estimation to refine the measurement and finish test

- GOSUB 380

 

280 'End of test processing

- CLS : PRINT : PRINT "You have finished your test."

- IF super% THEN

--- PRINT "You"; : GOSUB 610'Display ability estimate

--- PRINT nam$ + ", please call the test supervisor now."

--- MSG$ = "Is the test supervisor at the keyboard?": RESPONSE$ = "N"

--- WHILE RESPONSE$ <> "Y": GOSUB 810: WEND: GOSUB 640

- END IF

- RETURN'Show test results

 

- 'PRINT multiple LINE TEXT AND ONE SPACE

313- WHILE (LEN(TEXT$) > 79) OR (INSTR(TEXT$, "@") > 0)

' @ is the forced end of line code

----- LX = INSTR(MID$(TEXT$, 1, 80), "@")

----- IF LX > 0 THEN

-------- PRINT LEFT$(TEXT$, LX ‑ 1)

----- ELSE

-------- IX = 1

-------- WHILE IX <= 79:

----------- LX = IX: IX = INSTR(IX + 1, TEXT$ + " ", " ")

-------- WEND

-------- PRINT LEFT$(TEXT$, LX)

----- END IF

----- TEXT$ = MID$(TEXT$, LX + 1)

----- WEND: PRINT TEXT$: RETURN

'

'- Display the question on the screen and update ability estimate

330- CLS : PRINT "Question identifier:"; QTEXT$(QSELECT, 1): PRINT

- PRINT "Please select the best answer to the following question:"

- PRINT : TEXT$ = QTEXT$(QSELECT, 2): GOSUB 313

- PRINT : PRINT "The answer is one of:": PRINT

- FOR i = 1 TO maxanswer%

----- TEXT$ = MID$(ANSWER$, i, 1) + ". " + QTEXT$(QSELECT, i + 2): GOSUB 313

- NEXT i

- PASKED = PASKED + 1: PQUESTION(PASKED) = QSELECT

- QASKED(QSELECT) = 1'This question has been asked

- IF debug% THEN 'REPORT THE STATUS SO FAR

--- CURSROW% = CSRLIN: CURSCOL% = POS(0) ' SAVE POSITION

--- LOCATE 24, 1, 0 ' PENULTIMATE ROW

--- PRINT " item: SEQU NO- DIFFICULTY- ANSWER-- person: SCORE- MEASURE- SE";

--- LOCATE 25, 1, 0

--- PRINT USING _

---- "------- ####------ #####---- \ \------------- ###--- #####- #####";_

---- PASKED; FNU(QDIFF(QSELECT)); QTEXT$(QSELECT, correct%); presult; _

---- FNU(ABILITY); FNU(SE);

--- LOCATE CURSROW%, CURSCOL%, 1 'RESTORE POSITION

- END IF

'

'Estimate ability based on current score

380- PEXP = 0: PVAR = 0: FOR P = 1 TO PASKED

'Probability of success

- SUCCESS = 1 / (1 + EXP(QDIFF(PQUESTION(P)) ‑ ABILITY))

- PEXP = PEXP + SUCCESS: PVAR = PVAR + (SUCCESS * (1 ‑ SUCCESS)): NEXT P 'sum

- SE = SQR(1 / PVAR)'standard error of estimation = accuracy

- IF PVAR < 1 THEN PVAR = 1'limit change in estimates

430 ' Estimate low and high abilities for wrong and right answers

- ABILITY = ABILITY + ((presult ‑ PEXP) / PVAR)'ability so far

- ABILRIGHT = ABILITY + (1 / PVAR): RETURN' ability if next answer right

'

'- Select useful next question if needed for accuracy and available

460- QSELECT = 0: IF ACCURACY > SE OR PASKED = qcount THEN RETURN

- n = INT(qcount * RND) + 1'Starting point to look for suitable question

- ABILHALF = (ABILRIGHT + ABILITY) * .5: QSELECT = 0

- FOR QQ = n + 1 TO qcount + n

- IF QQ > qcount THEN Q = QQ ‑ qcount ELSE Q = QQ

- IF QASKED(Q) = 0 THEN ' this question has not yet been asked

--- i = QDIFF(Q)

--- IF i >= ABILITY AND i <= ABILRIGHT THEN QSELECT = Q: RETURN'found one

--- IF (QSELECT = 0) OR (ABS(i ‑ ABILHALF) < QHOLD) THEN

----- QSELECT = Q: QHOLD = ABS(i ‑ ABILHALF)' nearest available

--- ENDIF

- ENDIF

- NEXT QQ

- RETURN 'If none are very close, default to last possibility

'

'- Get and check person's answer to question: update ability if right

540- PRINT

- PRINT "Type the number of your selection here:";

- VALID$ = ANSWER$ + CHR$(19) 'Valid responses to questions on screen + Ctrl‑S

- GOSUB 1900

- IF RESPONSE$ = CHR$(19) THEN

----- PASKED = PASKED ‑ 1: QSELECT = 0: RETURN'FORCE END

- ENDIF

- n = VAL(RESPONSE$): PANSWER(PASKED) = n'Update answer array, update score

- i = VAL(QTEXT$(PQUESTION(PASKED), correct%))'Determine correct answer

- IF n = i THEN presult = presult + 1: ABILITY = ABILRIGHT'Update if correct

- RETURN

'

'- Display estimates of ability

610- PRINT " scored in the range from "; LTRIM$(STR$(FNU(ABILITY ‑ SE))); _

------ " to "; LTRIM$(STR$(FNU(ABILITY + SE)));

- PRINT " at about "; LTRIM$(STR$(FNU(ABILITY)));_

------- " after "; LTRIM$(STR$(PASKED)); " questions."

- RETURN

 

'- Record person's ability and answers on disk

640- PRINT "Summary report on questions administered to " + nam$

- PRINT "Identifier", "Difficulty", "Answer", "Right/Wrong"

- FOR P = 1 TO PASKED: Q = PQUESTION(P): n = PANSWER(P)

- IF n = VAL(QTEXT$(Q, correct%)) THEN

----- i = 1: TEXT$ = "RIGHT"

- ELSE

----- i = ‑1: TEXT$ = "WRONG"

- ENDIF

760 ' Is this response very unexpected?

- IF (ABILITY ‑ QDIFF(Q)) * i < ‑2 THEN TEXT$ = "SURPRISINGLY " + TEXT$

- PRINT QTEXT$(Q, 1), FNU(QDIFF(Q)), n, TEXT$

-- NEXT P

- PRINT nam$; : GOSUB 610: RETURN'Display estimated ability

 

-'- This routine checks for Yes/No answers ‑ no Enter key required

810- IF LEN(MSG$) < 61 THEN PRINT MSG$;- ELSE PRINT MSG$

- PRINT "- Yes or No (Y/N):"; : VALID$ = "NY": GOSUB 1900: RETURN

 

'- Load the question file (9 lines per question +blank) into an array

'FIND NUMBER OF OPTIONS IN QUESTION FILE

850- IF INSTR(UCASE$(QFIL$), ".SEC") > 0 THEN qsec% = ‑1

- n = 0: i = 0: OPEN QFIL$ FOR INPUT AS #1: TEXT$ = "A"

- WHILE NOT EOF(1) AND (TEXT$ + " " <> " "): GOSUB 1800: i = i + 1: WEND

- maxanswer% = i ‑ 5: ANSWER$ = LEFT$("123456789", maxanswer%)

- correct% = maxanswer% + 3: MEASURE% = maxanswer% + 4

- ' FIND NUMBER OF ITEMS

- maxitems = 1: WHILE NOT EOF(1): maxitems = maxitems + 1

----- FOR i = 1 TO maxanswer% + 4: GOSUB 1800: NEXT i

----- IF NOT EOF(1) THEN

-------- GOSUB 1800 'READ ANOTHER LINE

-------- IF TEXT$ <> "" THEN

--- --------PRINT "Blank line expected at line" + STR$(n)

----------- GOTO 930- 'WE HAVE AN ERROR

-------- ENDIF

----- ENDIF

- WEND

- CLOSE #1: RETURN

'

'READ IN QUESTIONS FILE ‑ ITEMBANK

870- qcount = 0: n = 0: qmean = 0

- OPEN QFIL$ FOR INPUT AS #1: WHILE NOT EOF(1)

- qcount = qcount + 1: i = 0

- WHILE i < maxanswer% + 4: i = i + 1: GOSUB 1800

- QTEXT$(qcount, i) = TEXT$

- WEND: IF NOT EOF(1) THEN GOSUB 1800

- IF VAL(QTEXT$(qcount, 1)) <= VAL(QTEXT$(qcount ‑ 1, 1)) THEN 930'Check ID

- i = VAL(QTEXT$(qcount, correct%))

- IF i < 1 OR i > maxanswer% THEN 'answer a possibility?

----- PRINT "Incorrect answer: " + QTEXT$(qcount, correct%)

----- GOTO 930

- ENDIF

- i = FNL(QTEXT$(qcount, MEASURE%))

- IF i < FNL("1") OR i > FNL("2000") THEN 'DIFFICULTY IN RANGE?

----- PRINT "Incorrect difficulty: " + QTEXT$(qcount, MEASURE%)

----- GOTO 930

- ENDIF

- QDIFF(qcount) = i

- qmean = qmean + i

- WEND: CLOSE #1

- IF qcount > 0 THEN qmean = qmean / qcount: RETURN'if all ok

- PRINT "No questions found"

930- PRINT "Error in question file, " + QFIL$ + ", at or before line "; n

- PRINT "Test session ended": STOP

'

'- Reestimation routine for question and test‑taker measurements

960- PRINT "Reading test‑takers' answers..."

- PASKED = 0: OPEN tfil$ FOR INPUT AS #2: WHILE NOT EOF(2)

- LINE INPUT #2, TEXT$: IF INSTR(TEXT$, "Test‑taker") = 0 THEN 1030

-- '- We have another test‑taker ‑ set his responses to unknown

- PASKED = PASKED + 1: FOR Q = 1 TO qcount: result%(PASKED, Q) = ‑1: NEXT Q

- PABILITY(PASKED) = 0: GOTO 1110

'

'- Read previous estimate of test‑taker's ability

1030- i = INSTR(TEXT$, "ability"): IF i = 0 OR PABILITY(PASKED) > 0 THEN 1050

- PABILITY(PASKED) = FNL(MID$(TEXT$, i + 8)): GOTO 1110

1050- i = INSTR(TEXT$, "identifier"): IF i = 0 THEN 1090'is this a question id?

- Q = VAL(MID$(TEXT$, i + 11))'Question identifier ‑ look up in table

- FOR i = 1 TO qcount: IF Q = VAL(QTEXT$(i, 1)) THEN Q = i: GOTO 1110

- NEXT i: Q = 0: GOTO 1110'if not found flag as zero which is unused

1090- IF INSTR(TEXT$, "RIGHT") > 0 THEN

------- result%(PASKED, Q) = 1: GOTO 1110 'save answer as correct

----- ENDIF

- IF INSTR(TEXT$, "WRONG") > 0 THEN result%(PASKED, Q) = 0 '1=right 0=wrong

1110- WEND: CLOSE #2

1120- PRINT "Totalling scores...": QTOTAL = 0: PTOTAL = 0: recount = 0

- FOR Q = 1 TO qcount: QASKED(Q) = 0: QSCORE(Q) = 0: NEXT Q

- FOR P = 1 TO PASKED: presult = 0: PSCORE(P) = 0: FOR Q = 1 TO qcount

----- n = result%(P, Q): IF n < 0 THEN 1180

----- presult = presult + 1: QASKED(Q) = QASKED(Q) + 1

----- PSCORE(P) = PSCORE(P) + n: QSCORE(Q) = QSCORE(Q) + n

1180- NEXT Q: IF presult = 0 THEN 1210

--- IF PSCORE(P) > 0 AND PSCORE(P) < presult THEN

------- PTOTAL = PTOTAL + 1: GOTO 1210

--- ENDIF

--- recount = 1: FOR Q = 1 TO qcount: result%(P, Q) = ‑1: NEXT Q

1210- NEXT P: FOR Q = 1 TO qcount: IF QASKED(Q) = 0 THEN 1240

-- IF QSCORE(Q) > 0 AND QSCORE(Q) < QASKED(Q) THEN

------ QTOTAL = QTOTAL + 1: GOTO 1240

-- ENDIF

-- recount = 1: FOR P = 1 TO PASKED: result%(P, Q) = ‑1: NEXT P

1240- NEXT Q

- IF PTOTAL < 2 OR QTOTAL < 2 THEN PRINT "Not enough data to reestimate": RETURN

- IF recount = 1 THEN 1120

- BIAS = 1 'modify this to allow for statistical bias

- FOR Q = 1 TO qcount: IF QASKED(Q) <> 0 THEN QDIFF(Q) = FNL(QTEXT$(Q, MEASURE%)) / BIAS

- NEXT Q: PADJ = 0: FOR P = 1 TO PASKED

- IF PSCORE(P) > 0 THEN

----- PABILITY(P) = PABILITY(P) / BIAS: PADJ = PABILITY(P) + PADJ

- ENDIF

- NEXT P- 'Sum current abilities to determine average ability level

'

1340 ' Now perform reestimation for 10 iterations.

- PRINT "Reestimating for"; PTOTAL; "test‑takers and"; QTOTAL; "questions"

- recount = 1: Cycle% = 1

- WHILE recount > 0 OR maxresidual > .1

- recount = 0: Cycle% = Cycle% + 1: maxresidual = 0

- PRINT "Estimation cycle no."; Cycle%

- PSUM = 0: FOR Q = 1 TO qcount: QEXP(Q) = 0: QVAR(Q) = 0: NEXT Q

- FOR P = 1 TO PASKED: IF PSCORE(P) = 0 THEN 1470

- PEXP = 0: PVAR = 0: FOR Q = 1 TO qcount: IF QASKED(Q) = 0 THEN 1420

- IF result%(P, Q) = ‑1 THEN 1420'Look at each valid answer

'Probability of success

- SUCCESS = 1 / (1 + EXP(QDIFF(Q) ‑ PABILITY(P)))

'Accumulate estimated scores

- QEXP(Q) = QEXP(Q) + SUCCESS: PEXP = PEXP + SUCCESS

'sum variance

- n = SUCCESS * (1 ‑ SUCCESS): QVAR(Q) = QVAR(Q) + n: PVAR = PVAR + n

1420- NEXT Q

- RESIDUAL = PSCORE(P) ‑ PEXP'difference between actual and estimated

- IF ABS(RESIDUAL) > maxresidual THEN maxresidual = ABS(RESIDUAL)

- IF PVAR > 1 THEN RESIDUAL = RESIDUAL / PVAR'amount to adjust by

- PABILITY(P) = PABILITY(P) + RESIDUAL'new ability estimate

'standard error

- PSE(P) = 1 / SQR(PVAR)

' ability sum across test‑takers

- PSUM = PSUM + PABILITY(P)

1470- NEXT P: PSUM = (PSUM ‑ PADJ) / PTOTAL'What is change in mean ability?

- FOR P = 1 TO PASKED

1480 'Keep mean ability of test‑takers constant

--- IF PSCORE(P) > 0 THEN PABILITY(P) = PABILITY(P) ‑ PSUM

- NEXT P-

- FOR Q = 1 TO qcount: IF QASKED(Q) = 0 THEN 1540'reestimate questions

--- RESIDUAL = QSCORE(Q) ‑ QEXP(Q)'difference between actual and estimated

--- IF ABS(RESIDUAL) > maxresidual THEN maxresidual = ABS(RESIDUAL)

--- IF QVAR(Q) > 1 THEN RESIDUAL = RESIDUAL / QVAR(Q)'amount to adjust by

--- QDIFF(Q) = QDIFF(Q) ‑ RESIDUAL'new question difficulty estimate

1540- NEXT Q: WEND: PRINT "Reestimation complete."

'

1550 ' Write out update item difficulties

- INPUT "What is the name of the updated question file"; QFIL$

- OPEN QFIL$ FOR OUTPUT AS #1: FOR Q = 1 TO qcount'- write out all questions

- FOR i = 1 TO correct%

--- PRINT #1, QTEXT$(Q, i): NEXT i: IF QASKED(Q) = 0 THEN 1600

--- i = QDIFF(Q) * BIAS: QDIFF(Q) = i 'statistical bias adjustment, if any

--- SE = BIAS / SQR(QVAR(Q))'- new difficulties

' insert new difficulty in line 9 of item bank

--- PRINT #1, FNU(i); ","; FNU(i ‑ SE); "‑"; FNU(i + SE); ",";

1600- PRINT #1, QTEXT$(Q, MEASURE%): PRINT #1, "": NEXT Q:

--- FOR Q = 1 TO qcount

--- PRINT #1, Q; FNU(QDIFF(Q) * BIAS)

--- NEXT Q

--- CLOSE #1'Append old estimate

 

' Now rewrite the test‑taker file with revised abilities

1620- INPUT "What is the name of the revised test‑taker file"; TREVFIL$

- IF tfil$ = TREVFIL$ THEN 1620'must be a different file

- OPEN TREVFIL$ FOR OUTPUT AS #1: PASKED = 0'read previous test‑taker file

- OPEN tfil$ FOR INPUT AS #2- 'output revised test‑taker file

- WHILE NOT EOF(2): LINE INPUT #2, TEXT$: PRINT #1, TEXT$'copy over

- IF INSTR(TEXT$, "Test‑taker") = 0 THEN 1720'is this next test‑taker ?

- PASKED = PASKED + 1: IF PSCORE(PASKED) = 0 THEN 1720'is his ability revised?

- ABILITY = PABILITY(PASKED) * BIAS: SE = PSE(PASKED) * BIAS'remove bias

1700 ' Update test‑taker ability

- PRINT #1, "Revised estimated ability:"; FNU(ABILITY)

- PRINT #1, "Probable ability range:"; FNU(ABILITY ‑ SE); "‑"; FNU(ABILITY + SE)

1720- WEND

 

1703 ' output the matrix of Responses for external analysis

- PRINT #1, ""

- FOR P = 1 TO PASKED

- x$ = "Responses="

- FOR Q = 1 TO qcount: x$ = x$ + LEFT$(LTRIM$(STR$(result%(P, Q))), 1): NEXT Q

- PRINT #1, x$

- NEXT P

- CLOSE #2: CLOSE #1: tfil$ = TREVFIL$ 'Use new test‑taker file if testing continues

- RETURN

'

' READ IN THE NEXT LINE OF THE DATA FILE

1800- TEXT$ = ""

---- LINE INPUT #1, ttt$

------ IF qsec% THEN

-------- FOR tti% = LEN(ttt$) TO 1 STEP ‑1

---------- ttx% = ASC(MID$(ttt$, tti%, 1))

---------- IF ttx% >= 32 THEN

---- MID$(ttt$, tti%, 1) = CHR$((ttx% AND 224) + (((ttx% AND 31) + 16) AND 31))

---------- ENDIF

-------- NEXT tti%

------ END IF

------ ttt$ = RTRIM$(ttt$): n = n + 1

---- IF LEN(ttt$) > 0 THEN

' continuation is \, forced end of line is @

-------- WHILE (RIGHT$(ttt$, 1) = "\") OR (RIGHT$(ttt$, 1) = "@")

----------- IF RIGHT$(ttt$, 1) = "\" THEN MID$(ttt$, LEN(ttt$), 1) = " "

----------- TEXT$ = TEXT$ + ttt$

----------- LINE INPUT #1, ttt$

------ IF qsec% THEN

-------- FOR tti% = LEN(ttt$) TO 1 STEP ‑1

---------- ttx% = ASC(MID$(ttt$, tti%, 1))

---------- IF ttx% >= 32 THEN

--- MID$(ttt$, tti%, 1) = CHR$((ttx% AND 224) + (((ttx% AND 31) + 16) AND 31))

---------- ENDIF

-------- NEXT tti%

------ END IF

------------- ttt$ = RTRIM$(ttt$): n = n + 1

-------- WEND

----- END IF: TEXT$ = TEXT$ + ttt$

-- RETURN

'

' READ IN A VALID KEY ‑ VALID RESPONSES IN VALID$

1900- CURSROW% = CSRLIN: CURSCOL% = POS(0): RESPONSE$ = "ZZ"

1901- WHILE INSTR(VALID$, RESPONSE$) = 0

---- LOCATE CURSROW%, CURSCOL%, 1

---- RESPONSE$ = INKEY$: WHILE LEN(RESPONSE$) = 0: RESPONSE$ = INKEY$: WEND

---- RESPONSE$ = UCASE$(RESPONSE$)

-- WEND

-- PRINT RESPONSE$;

-- LOCATE CURSROW%, CURSCOL%, 1' CONFIRM OR DENY

-- KEYSTR$ = INKEY$: WHILE LEN(KEYSTR$) = 0: KEYSTR$ = INKEY$: WEND

-- IF KEYSTR$ <> CHR$(13) THEN RESPONSE$ = KEYSTR$: GOTO 1901

-- WHILE LEN(INKEY$) <> 0: WEND

- RETURN

 

'

' add next test‑taker to the file

2660- OPEN tfil$ FOR APPEND AS #1

- pl$ = "Test‑taker's name: " + nam$: GOSUB 658

- pl$ = "Estimated ability:" + STR$(FNU(ABILITY)): GOSUB 658

- pl$ = "Probable ability range:" + STR$(FNU(ABILITY ‑ SE)) + _

-------- "‑" + STR$(FNU(ABILITY + SE)): GOSUB 658

- pl$ = "Score =" + STR$(presult) + " out of" + STR$(PASKED): GOSUB 658

- pl$ = "": GOSUB 658

- rstring$ = STRING$(qcount, "‑")

- FOR P = 1 TO PASKED: Q = PQUESTION(P): n = PANSWER(P)

- pl$ = "Question identifier:" + QTEXT$(Q, 1): GOSUB 658

- pl$ = "Estimated difficulty:" + STR$(FNU(QDIFF(Q))): GOSUB 658

- pl$ = "Question text:" + LEFT$(QTEXT$(Q, 2), 50): GOSUB 658

- pl$ = "Answer:" + STR$(n) + ", " + LEFT$(QTEXT$(Q, n + 2), 50): GOSUB 658

-- '- Find if answer is right or wrong and if unexpectedly so.

- IF n = VAL(QTEXT$(Q, correct%)) THEN

------- i = 1: TEXT$ = "RIGHT"

------- MID$(rstring$, Q, 1) = "1"

--- ELSE

------- i = ‑1: TEXT$ = "WRONG"

'output the wrongly chosen distractor

------- MID$(rstring$, Q, 1) = MID$("ABCDEF", n, 1)

--- END IF

- IF (ABILITY ‑ QDIFF(Q)) * i < ‑2 THEN TEXT$ = "SURPRISINGLY " + TEXT$

- pl$ = "This answer is: " + TEXT$: GOSUB 658

- pl$ = "": GOSUB 658 'blank line after answer

- NEXT P

- pl$ = "Responses=" + rstring$ + " " + nam$: GOSUB 658

- CLOSE #1

- RETURN

'

' check for security coding in operation

658- IF INSTR(UCASE$(tfil$), ".SEC") > 0 THEN

------ FOR tti% = LEN(pl$) TO 1 STEP ‑1

---------- ttx% = ASC(MID$(pl$, tti%, 1))

---------- IF ttx% >= 32 THEN

--- MID$(pl$, tti%, 1) = CHR$((ttx% AND 224) + (((ttx% AND 31) + 16) AND 31))

---------- ENDIF

------ NEXT tti%

-- END IF

-- PRINT #1, pl$

-- RETURN

 

' end of UCAT program.

 

 

Program 2:- SECURE.BAS to encrypt and decrypt the data files.

 

' Here is a separate BASIC program to institute a simple

' security recoding to render the item bank unreadable.

' ascii values must be above 31

' take the low order bits and add 15 to them and then save

CLS

' Mainline of code: check command line switches.

' this program can be invoked with command line switches.

' COMMANDLINE$=COMMAND$

' if the line above is not supported, you cannot use DOS command line prompts

' enter your prompt here:

- INPUT "NAME OF ITEMBANK FILE TO ENCRYPT OR DECRYPT: ", COMMANDLINE$

 

f$ = UCASE$(COMMANDLINE$)

f% = INSTR(f$, ".")

IF f% = 0 THEN ofile$ = f$ ELSE ofile$ = MID$(f$, 1, f% ‑ 1)

IF INSTR(COMMANDLINE$, ".SEC") = 0 THEN

- ofile$ = f$ + ".SEC"

- PRINT "Writing secure file to " + ofile$

ELSE

- PRINT "Writing unsecured file to " + ofile$

END IF

OPEN f$ FOR INPUT AS #1

OPEN ofile$ FOR OUTPUT AS #2

WHILE NOT EOF(1)

------ LINE INPUT #1, l$

------ FOR i% = LEN(l$) TO 1 STEP ‑1

---------- x% = ASC(MID$(l$, i%, 1))

---------- IF x% >= 32 THEN

---- MID$(l$, i%, 1) = CHR$((x% AND 224) + (((x% AND 31) + 16) AND 31))

---------- ENDIF

------ NEXT i%

------ PRINT #2, l$

WEND

CLOSE

PRINT "converted"

SYSTEM

STOP