2.2.1 Overview of the Method
This method identifies misvalued CPT [Current Procedural Terminology] codes in terms of either total or intra-service work based on a small-group panel comparison of codes within families. The objective is to identify statistical outliers that appear to be either misaligned or compressed in terms of overall physician work effort employing a simpler approach than magnitude estimation. The method is based on original research undertaken by Dr. Robert Florin, a retired neurosurgeon and current member of the AMA RUC [American Medical Association Relative Value Update Committee]. Rasch paired comparison combines methods developed from educational research and statistical regression to, first, reorder families of codes, then convert the new cardinal scoring system to total work RVUs [Relative Value Units]. This method is likely to be only one of a number of psychometric methods that could be used to obtain estimates on physician work. Time and resource constraints precluded a more exhaustive search of alternative methods.
2.2.2 Background
After the first 5-year review of the Medicare fee schedule, Dr. Florin began a systematic study of new ways of identifying ranking anomalies among families of codes as well as responding to the general impression among many surgeons that the RBRVS [Resource-based Relative Value System/Scale] scales were compressed in certain families-and possibly across families and specialties. The RUC approach to generating RVU weights for new procedures suggested a form of paired comparison. That is, the RUC asks surveyed physicians (usually through medical societies) to report the estimated time and complexity bounded by the two reference set procedures closest to the new code in question. Recognizing the burden on respondents and problems of sample bias, Dr. Florin turned to an alternative psychometric method for generating a cardinal rank ordering of small families of procedures. This procedure does not require extensive surveys; only a modest number of participants (20-30) who could quickly fill out a page or two of comparisons as part of another meeting.
The underlying approach is called Rasch measurement analysis,
first developed by Georg Rasch in
1950s-1970s. It has been used in a wide variety of disciplines
including education and test grading, health outcomes
research, physiology, psychophysics, writing performance,
mathematics, marketing, physics, and ethical valuation.
Paired comparison is a sub-analysis under the broader rubric of
Rasch
analysis. Rasch methods are grounded in the psychometric literature
dealing with how to "count things." Rasch measurement models are
based on a simple performance measure,
Lni = Bn/Di,
where Bn = the level of ability of the n-th person
(i.e., test taker or rater) and Di = the difficulty of
the i-th test item (Andrich, 1988). The measure incorporates both
the abilities of the test taker (if relevant) and the difficulty of
the items (questions) on the test. The greater the ability of the
test taker, the higher the Rasch performance measure while the
greater the item difficulty the lower the score or rating. (For
physicians rating the work involved between two procedures, the
basic Rasch ratio is reversed, with higher difficulty a positive
factor in the numerator and the physician's ability to perform
difficult procedures in the
denominator.)
The probability of observing a particular Rasch score is assumed
to be distributed logistically as
(Lni) = Lni/(1 + Lni) =
(Bn/Di)/Gni,
where Gni = 1 + (Bn/Di) is a
normalizing factor. On any item scored
zero or one (e.g., right versus wrong, more versus less), the
probability of scoring a 1 is Lni/(1 + Lni),
while the probability
of a zero is 1/(1 + Lni). Note that the two probabilities
sum to
1.0. Thus, the Rasch is a cumulative model. As the tester's ability
increases relative to the difficulty of the test items, the measure
increases. Conversely, the more difficult the test items relative
to a tester, the lower the score.
Rasch measurement is flexible enough to rate both the abilities of different testers and the relative difficulties of the test items. In evaluating physician work, we would like differences in raters' "abilities" (i.e., perceptions of procedure difficulty) to cancel out, leaving just the relative difficulties of the procedures. This can be done by calculating the odds of a person's rating of work on two items:
Pb(1,0)/Pb(0,1) = [(Bn/D1)/Gn]/[(Bn/D2)/Gn] = D2/D1
where Pb(1,0) = the probability that a single rater would rate the first item a 1 (or more work) versus a second item (=0). Note that the rater's ability cancels out when odds ratios are taken. Also note that the odds of rating item 1 as more work depends positively on the difficulty of item 2 and inversely with item 1. This is backwards and is easily corrected by recoding the procedure with more work as a zero.
Next, in rating two items, the likelihood of either being rated more work can be expressed as:
(1a) Prob12(1,0) = 1/D1//(1/D1 + 1/D2) = D2/(D1+D2)
(1b) Prob21(0,1) = 1/D2//(1/D1 + 1/D2) = D1/(D1+D2)
where Prob12(1,0), for example, is the probability of rating item 1 more work than item 2, conditional on the fact that the single rater is comparing only the two procedures and not both to a third procedure. Note that the rater's ability cancels out in the numerator and denominator (leaving only 1's). Multiplying through the top and bottom of (Ia) by D2 and (Ib) by D1 gives the last expression in the probability formulas. Thus, the probability of rating procedure 1 as more work than procedure 2 depends on the difficulty of procedure 2 as a proportion of the combined difficulty of the two procedures. (Again, the ratings need to be reversed if procedure 1 is regarded as more work.) Note that the two probabilities sum to 1.0.
To build up an estimate of the relative difficulties of the two items, Rasch relies on multiple respondents scoring the two items as more or less work (which will be expanded to include more items below). The probability of observing a given frequency of 0,1 responses for the two items can be determined using a binomial distribution, i.e.,
(2) Pb(f12,f21; D1,D2) = [F12!/f12f21!] Prob12f12Prob21F12-f21
where f12,f21 = positive ratings for item 1 over 2 and 2 over 1, respectively; and F12 = the total number of times items 1 and 2 are rated. Eq. (2) gives the probability of observing the exact combination of positive ratings for items 1 and 2 ( = f12,f21) based on the true underlying probabilities of observing the individual patterns, (1,0) and (0,1), for the two items. Note that the relative difficulty of the two items, or work effort, is embedded in the Prob-probabilities (which add to 1.0).
Eq. (2) can be expanded to consider all pairs in a set of many items, thereby producing a likelihood function of all pairs. The question then becomes: What is the set of individual probabilities, Probij, that maximize the likelihood of observing the set of rater 0,1 scores, fij, for all the individual pairs? This is determined by first taking logs of the overall likelihood function (derived by multiplying (2) by all ij combinations), differentiating with respect to the Probij's (or the deltaij's = logs of the Dij's embedded in the Probij's), and setting the resulting equations for the i-items equal to zero:
(3) -Sumj fij + Sumj Fij Probij = 0 i=l ... L .
The constraints are then solved iteratively for the optimizing Probij's. In order to produce absolute ratings, instead of relative difficulties, a further constraint is imposed that the sum of the (logged) difficulties (the deltaij's) are set equal to zero. Hence, some items will be scored negatively, in logs, and others, positively. Taking antilogs gives positive final item scores greater or less than 1.0. Because the probabilities are not independent, they must be solved iteratively to meet the conditions for the L equations implied in (3). The maximizing conditions implied by (3) require that the weighted sum of probabilities that a particular item will be preferred over other items (i.e., rated higher work) be equal to the total number of times the item is rated positively, or greater work, across all paired comparisons. The weights are the number of times a particular pair is evaluated (i.e., the Fij). The F-weights effectively normalize for the number of times a particular item is rated, which is necessary in that an item will likely receive more positive scores the more times it is compared with other items. Relative, and absolute, difficulty of each procedure compared to others is determined by the frequency with which it is rated more difficult with respect to each of the other alternatives.
An added flexibility of the Rasch method is its linking ability when raters do not rate all pairs. Linking is crucial in devising tests of varying difficulty when different groups of test takers are not given all questions on a test (or may not respond to all of them because of their difficulty). This is called tailored testing. What is required is some overlapping items. So long as some items are rated by both groups (e.g., general and neurosurgeons), Rasch methods can extend the results to produce a single common scale.
Dr. Florin has personally conducted several small-group rating sessions using Rasch methods. In early 1998, he took advantage of a group of over 100 neurosurgeons to rerank 12 laminectomy codes from the CPT manual (63001-63047). The audience filled out a ranking sheet containing matched pairs of codes. According to the example rating sheet used by the participants, physician work was defined as "the time of the operation [times] the intensity and complexity of the procedure." The responses were then analyzed at the University of Chicago by Prof. Ben Wright using Rasch computer software. Several codes were found to be misaligned. Procedure 63011 was seriously undervalued while 63042 was seriously overvalued. In the Spring of 1998, Dr. Florin conducted another paired comparison study; this time on 19 surgical operations in the basic reference set. He surveyed 9 general surgeons for the ranking, which ranged from CPT 99291, Critical Care, 1 hour (RVU = 4) to 48150, Pancreatectomy (RVU = 43.48). While all the codes except for Critical Care were surgical in nature, they spanned the range of surgeries across families and specialties. Again, Dr. Florin found a few codes over- or undervalued and out of order. On the other hand, many new RVU values were quite similar to original values, which is interesting given the wide range of codes and the fact that only 9 general surgeons were used for rating purposes.
The Rasch methodology involves a few steps that produce a linear scaling of codes (called Rasch measures) based on matching pairs of codes. Respondents are given one or two pages of code pairs and are asked to circle the code on each line that involves the most work (however defined). No single respondent is given all the possible pairs, and each respondent has a set of overlapping pairs that "anchor" responses across respondents. The results are then inputted into Rasch computer software that keys on the log-odds ratios of one code's work effort versus another. The software puts the codes in rank order in terms of work effort based on the frequency of times respondents say they involve more or less work relative to other codes. It also spreads out the ranking onto a linear scale.
Once the codes are "Rasched", Dr. Florin next converts the arbitrary psychological scale into new RVUs. The conversion is done based on an Ordinary Least Squares regression of Rasch scores onto existing RVU values. This amounts to a linear transformation of Rasch scores into RVUs, thereby maintaining the proportionality of the Rasch measures. Finally, each code's actual current RVUs are compared to the RVUs "predicted" by its Rasch score using the linear regression line.
Suppose the raters' results based on paired comparisons produces a lower Rasch score for code #1 relative to code #2. Both Rasch scores would have a predicted number of RVUs based on linear regression. Then, each code's actual RVUs would be compared with its Rasch-predicted value. If code #1 was misaligned, its Rasch-predicted RVUs might be considerably lower than its actual RVUs; lower, even, than code #2's actual RVUs.
2.2.3 Data Requirements
Data requirements for paired comparison analyses are minimal. A small group of clinicians is required for making the paired comparisons - either at a meeting or possibly surveyed using fax or e-mail. Participants work "blind" in not knowing or discussing the way in which their colleagues are rating pairs of codes.
Worksheets would be created with 40-60 code pairs on 1-2 pages with some overlapping pairs on different worksheets to link respondent ratings. Circled codes implying more work are then used to construct a matrix reporting the number of times one code was rated higher than another and vice-versa.
2.2.4 Detailed Description of the Method
Step 1: Identify a representative small group panel of clinical experts (at least 10) familiar with a given family of codes.
Step 2: Distribute in a meeting or by mail a worksheet with 40-60 code pairs in the family and ask participants to circle the code in each pair requiring more work effort. Different definitions of work effort could be tested with the same group using separate worksheets. For example, work could be defined, first, as total work for a global 90-day service and. second, only for the intra-operative work.
Step 3: Prepare a matrix of survey results on the likelihood of one code being preferred to another for input into the Rasch software.
Step 4: Output from the software produces a Rasch yardstick graph listing each code from mos. to least work effort scaled, visually, on the graph. Considerable statistical output on mode accuracy and reliability is also produced, such as model root mean square error and a Chi square test of equal RVUs for all procedures.
Step 5: Create a table listing each procedure ordered by CPT code or by current RVUs. Include a code descriptor, code number, and current MFS [Medicare Fee Schedule] work units.
Step 6: Convert Rasch scores to RVUs by first regressing Rasch scores on current RVUs. Then generate a predicted (revised) RVU using each code's Rasch score.
Step 7: Transfer the new Rasch-based RVUs to your table and create a new column showing the difference between the old and new codes. Also create a Rasch-based rank order column showing misaligned codes at a glance.
Step 8: Based on the overall degree of misalignment, consider the family "aligned" and in no further need of investigation or "misaligned" and in need of further study to verify the small-group informal Rasch-based results.
Step 9: The Rasch software also indicates codes that appear far out of line with the other codes on a linear scale. These may be candidates for detailed study and may suffer from poor work definitions or simply not belong with the family of codes for some reason.
A Rasch analysis could be performed on a small or large family of codes by specialty.
2.2.5 Illustrative Example
As an example of how paired comparison analysis is performed, consider the examination of laminectomy codes, taken from Dr. Florin's research. Figure 2-1 shows a worksheet of pairs of laminectomy codes ranging from 63001 to 63047. In this example, work is defined as intra-service = surgery time x intensity. The reviewer is instructed to read across the rows one at a time and circle the code involving greater work. For example, on the first line, the reviewer is asked to rate whether 63011 involves more or less work than 63030. (The 1997 MFS work RVUs for 63011 and 63030 are 13.4 and 11.1, respectively.) The alphabetic codes at the far left signify the paired grouping. For this evaluation, code 63011 = A and 63030 = B. Several of the raters will rate combination AB, gb, etc., building up the probability matrix of relative work. Each evaluator would be given a similar, but not identical, worksheet. Some identical comparisons would appear on several worksheets to support linking the responses across raters.
Paired Comparisons for Revaluation of Laminectomy Codes | ||||
| Group 1 | ||||
| AB | 63011 | LAMINECTOMY /SACRAL REGION | 63030 | LAMINOTOMY, ONE LEVEL FOR HERNIATED DISC, UNILATERAL, LUMBAR |
| gb | 63017 | LAMINECTOMY /EXPL/DECOMP, LUMBAR CORD OR CAUDA EQUINA, >2 SEGS | 63030 | LAMINOTOMY, ONE LEVEL FOR HERNIATED DISC, UNILATERAL, LUMBAR |
| DE | 63047 | LAMINECTOMY FR COMPLETE DECOMPR, STENOSIS, LUMBAR ONE LEVEL | 63006 | LAMINECTOMY /EXPL /DECOMP CORD &/OR CAUDA EQUINA, 1-2 SEGS, LUMBAR |
| FG | 63001 | LAMINECTOMY FOR EXPLORATION /DECOMP CORD, 1 OR 2 SEGS, CERVICAL | 63017 | LAMINECTOMY /EXPL/DECOMP, LUMBAR CORD OR CAUDA EQUINA, >2 SEGS |
| . . . |
. . . |
. . . |
. . . |
. . . |
| AL | 63011 | LAMINECTOMY /SACRAL REGION | 63046 | LAMINECTOMY FOR COMPLETE DECOMPR, STENOSIS, CERVICAL, ONE LEVEL |
| CE | 63020 | LAMINOTOMY, ONE LEVEL FOR HERNIATED DISC, UNILATERAL, CERVICAL | 63005 | LAMINECTOMY /EXPL/DECOMP CORD &/OR CAUDA EQUINA, 1-2 SEGS, LUMBAR |
| IO | 63042 | LAMINOTOMY FOR DISC, ANY LEVEL, EXTENSIVE OR RE-EXPLORAT, LUMBAR | 63047 | LAMINECTOMY FR COMPLETE DECOMPR, STENOSIS, LUMBAR ONE LEVEL |
| GJ | 63017 | LAMINECTOMY /EXPL/DECOMP, LUMBAR CORD OR CAUDA EQUINA, >2 SEGS | 63015 | LAMINECTOMY FOR EXPLORATION /DECOMP, CERVICAL CORD, >2 SEGS |
| Compare the pair of codes in each row
(left to right) and circle the CPT cod of
the one that requires more physician work. Physician work = the time of the operation x the intensity and complexity of the procedure | ||||
Figure 2-2 shows the resulting Rasch yardstick of linear measurement. This particular panel more often rated code 63040, Cervical laminotomy with decompression and/or excision of herniated disk and re-exploration, as more work than any other code in the family. Conversely, a lumbar laminotomy (63030) was rated least work relative to all the other codes. The linear measures, ranging from 020 to 158, have been derived and standardized (to code 63047) based on the frequency of respondent indications of more or less work. Based on Rasch measures, code 63047 is 5 times more work than 63030. Code 63040 is rated 58 percent more work than code 63047. The yardstick shows at a glance how similar or different the codes are in terms of perceived work. For example, 63016 and 63001 are considered essentially equal in terms of work while both are roughly double the work of 63020 and 63045.
|
RASCH LINEAR
MEASURE of Amount of Physician Work |
RASCH Procedure Codes YARDSTICK (Laminectomy) |
| . | |
| 158 K | 63040 Laminotomy::disc any level extensive or re-explor CERVICAL |
| . | . |
| 146 J | 63015 Laminectomy:explor/decomp CERVICAL cord >2segs |
| . | .. |
| 129 A | 63011 Laminectomy:sacral region |
| 124 H | 63016 Laminectomy:explor/decomp thoracic cord >2segs |
| 123 F | 63001 Laminectomy:explor/decomp cord 1-2 segs, CERVICAL |
| . | . |
| . | . |
| 100 D | 63047 Laminectomy::complete decomp stenosis LUMBAR 1 level |
| 099 E | 63005 Laminectomy::explor/decomp cord &/or cauda equina, 1-2 segs, LUMBAR |
| . | . |
| 083 L | 63042 Laminotomy:: disc any level extensive or re-explor LUMBAR |
| . | . |
| 076 C | 63020 Laminotomy::1 level for herniated disc, unilateral, CERVICAL |
| 075 I | 63045 Laminectomy:complete decomp stenosis CERVICAL 1 level |
| . | . |
| 067 G | 63017 Laminectomy:explor/decomp LUMBAR cord or cauda equina >2 segs |
| . | . |
| . | . |
| . | . |
| 020 B | 63030 Laminotomy::1 level for herniated disc, unilateral, LUMBAR |
| . | |
| SOURCE: Based on Rasch Computer Software developed by J.M. Linacre & B.D. Wright | |
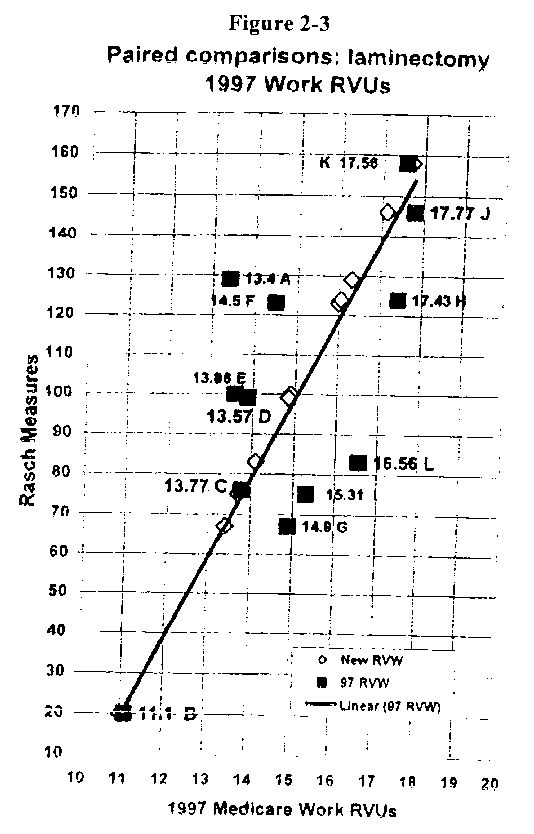
Figure 2-3 shows the linear regression relationship between the Rasch scores and the 1997 RVUs. RVUs predicted by the Rasch scores are indicated by the white diamonds along the linear line. A companion figure (not shown) provides 95 percent confidence bands (Cl's) to the left and right of the regression line.

Table 2-2 ranks the 12 codes under consideration from least to most intra-service work according to their Rasch scores. Also listed are the actual 1997 MFS RVUs. The column headed New Work RVUs are based on predicted RVUs from a linear regression of Rasch scores on 1997 RVUs. They automatically rise from lowest to highest in accord with the Rasch ranking. The last column shows how the codes are actually ranked based on the 1997 RVUs.
| CPT | Rank Order based on Paired Comparison Descriptor Procedure: Spine; laminectomy & laminotomy |
1997 MFS Work RVUs | Sort Paired Comparison (Rasch Measures) |
New Work RVUs | 1997 Rank Order | |
| B | 63030 | LAMINOTOMY, ONE LEVEL FOR HERNIATED DISC, UNILATERAL, LUMBAR | 11.1 | 20 | 11 | 1 |
| G | 63017 | LAMINECTOMY/EXPL/DECOMP, LUMBAR CORD OR CAUDA EQUINA, >2 SEGS | 14.9 | 67 | 13 | 7 |
| I | 63045 | LAMINECTOMY/COMPLETE DECOMPR, STENOSIS, CERVICAL, ONE LEVEL | 15.31 | 76 | 14 | 8 |
| C | 63020 | LAMINOTOMY, ONE LEVEL FOR HERNIATED DISC, UNILATERAL, CERVICAL | 13.77 | 76 | 14 | 5 |
| L | 63042 | LAMINOTOMY FOR DISC, ANY LEVEL, EXTENSIVE OR RE-EXPLORAT, LUMBAR | 16.58 | 83 | 14 | 9 |
| E | 63005 | LAMINECTOMY/EXPL/DECOMP CORD &/OR CAUDA EQUINA, 1 OR 2 SEGS, LUMBAR | 13.88 | 99 | 15 | 6 |
| D | 63047 | LAMINECTOMY/COMPLETE DECOMPR, STENOSIS, LUMBAR, ONE LEVEL | 13.57 | 100 | 15 | 4 |
| F | 63001 | LAMINECTOMY FOR EXPLORATION/DECOMP, CORD, 1 OR 2 SEGS, CERVICAL | 14.5 | 123 | 16 | 3 |
| H | 63016 | LAMINECTOMY FOR EXPLORATION/DECOMP, THORACIC CORD >2 SEGS | 17.43 | 124 | 16 | 10 |
| A | 63011 | LAMINECTOMY/SACRAL REGION | 13.4 | 129 | 16 | 2 |
| J | 63015 | LAMINECTOMY FOR EXPLORATION/DECOMP, CERVICAL CORD >2 SEGS | 17.77 | 146 | 17 | 12 |
| K | 63040 | LAMINECTOMY FOR DISC, ANY LEVEL, EXTENSIVE OR RE-EXPLORAT, CERVICAL | 17.58 | 158 | 18 | 11 |
|
SOURCE; Florin, R.E. "A Study of Relative Work Values for a Series of Laminectomy Codes using a Technique called Paired Comparisons," unpublished study based on responses of a panel of neurophysicians, March 1998. | ||||||
From Figure 2-3 and Table 2-2 it would appear that code 63011 (A) is most out-of-line. According to the panel's evaluation, this code should be rated much higher (10th of 12) in the family in terms of work instead of second lowest. Code 63001 also appears to be somewhat undervalued. Several other codes, by contrast, appear overvalued, including 63042 and 63045. Based on the 95 percent Cl's, 3-4 procedures seem clearly misaligned, i.e., 63011, 63042, 63045, and 63016.
From this study, one could conclude that (a) the family of laminectomy codes are in need of detailed examination, and (b) code 63011 may be seriously undervalued while a couple of codes involving laminotomies with re-exploration may be overvalued. Of course, the difference in this example may simply be due to the difference in how work was defined. For paired comparison valuation, only intra-service work was rated while the 1997 MFS RVUs naturally include pre/post work as well. In a real application, identical measures of work would be used. However, the example illustrates the technique. The results could be forwarded to the RUC for intensive review to determine if, in fact, the work of a few of the codes has changed. The suspect codes would be identified, although the RUC may not wish to share this information with any survey respondents they collect data from.
2.2.6 Strengths and Weaknesses of Method
Strengths
Structuring small-group valuations of CPT codes using Rasch measurement techniques provides a systematic psychometric underpinning to the rating system. An extensive formal literature exists on using individual perceptions about differences in items to construct a cardinal scale ranking codes from most to least work (defined as intra-service or total).
Rasch measurement places a minimal burden on respondents, who can generally decide which of two codes is more work within a few seconds. Filling out an entire worksheet may require 10- 15 minutes.
Unlike magnitude estimation, Rasch methods do not require clinicians to quantify the relative work of procedures.
Small groups of clinicians would not have to meet in one place but could easily fill our their worksheets off-site and fax or e-mail them to an evaluator. Working independently would avoid the considerable time required of an entire panel of clinicians discussing and reaching consensus on the ordering and precise RVUs of codes.
The Rasch method has been validated for families of services within a specialty and has been tested for within specialty adjustment of RVUs.
The method could be used as a first-stage approximation to a more in-depth realignment process. If applied to many families (25-50) based on off-site worksheets sent to several specialty panels, the resulting Rasch measurements may be able to systematically eliminate many families from further review as well as identifying I or 2 very problematic codes within a family.
Potential Weaknesses
Rasch rank orderings will be more or less sensitive to the number and selection of clinical participants depending upon the heterogeneity of experience of the panelists. Surgeons, for example, may see systematically different patients undergoing a particular operation, e.g., benign versus malignant stomach tumor; female versus male bypass surgery. The efficient number of respondents is not known beforehand.
Rasch rank orderings will be more or less sensitive to the equivocalness of the work definitions in a family of codes, e.g., is total work being rated or just intraservice work. This could produce unstable, inconsistent pairing by the respondents and raise questions about the existence of a linear relation among the codes.
Practitioners may not be familiar with all the codes under study, although the method can handle blank responses. Ms would add error and uncertainty to some of the codes. Participants ideally would be fairly familiar with each procedure being paired and what a typical patient and practice modality would involve.
Rasch measures would produce an alternative ordering of codes and even a new set of RVUs through regression analysis. Criteria would have to be established to guide HCFA analysts in deciding whether to leave the old codes unchanged, investigate 1 or 2 in-depth, or possibly replace with the new Rasch-based RVUs.
Converting Rasch measures to predicted RVUs using a linear regression could compress values at the tails of the distribution. A nonlinear predicting equation may give a better fit.
Rasch measures and resulting rank order and RVUs do not explain why some codes seem misaligned. Detailed Rasch statistics, however, can be used to identify an outlier respondent who is disproportionately influencing the anomalous results. Reasons for unusual rankings can be gleaned from the respondent, which could lead to recommendations to split codes.
Care would have to be taken to exactly specify the type of work being rated, e.g., total work versus intra-service work.
Given that the work component of the MFS is based on magnitude estimation, it could be inconsistent to revise one or more families of codes based on paired comparison methods.
Rasch paired comparison does not necessarily allow for face-to-face discussion which may produce biased results.
While the Rash method has been validated for families of services within a specialty, Us method has not been validated for reviewing and adjusting RVUs for codes in families performed by different specialities.
2.2.7 Likely Response by Key Stakeholders
2.2.8 Time Frame
The Rasch method identifies misvalued CPT codes in terms of either total or intra-service work based on a small group comparison of pairs of codes' work estimates within small clinical families. These comparisons may be made in a face-to-face meeting or through the use of a mail survey instrument. The time frames for both of these data collection modes have been discussed previously in 2.1.8. The primary difference between the two modes in terms of time is one month, the face-to-face meeting method generally takes longer because of scheduling challenges. It is anticipated that identification of inappropriately valued work RVUs using the Rasch paired comparison method can be completed within five months from the start of the project, if a mail survey mode is used. A six month time frame should be anticipated if a face-to-face data collection mode is used. Exhibit 2-3 displays the timing of the tasks described in Section 2.2.4 for conducting a Rasch paired comparison of work RVUs.
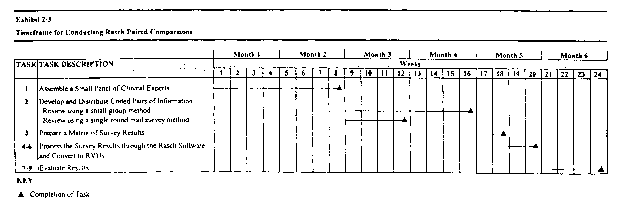
Task 1: Assemble a small panel of clinical experts
The first step will be to determine the number and composition of the panels that will be used in this method. We estimate that it will take approximately two months to assemble the necessary panels of clinical experts. During this time, we recommend HCFA seek nominations from a variety of different physician organizations, e.g., the American Medical Associations Relative Value Update Committee, specialities societies, and local medical associations, to ensure broad representation to the panels. Materials need to be distributed to the targeted physician organizations specifying the qualifications of the physicians being sought, the proposed dates for the meeting and the location, if a face-to-face meeting will be conducted, or the time period during which the physicians are expected to complete the paired comparison task, if a mail survey mode is selected. Follow-up with nominated physicians to ensure their interest and availability also will be necessary as will written confirmation of their appointment to a panel, once the final selections have been made.
Task 2: Develop and distribute information to the panelists
We estimate that the mail survey can be conducted during the third month or the face-to-face meetings can be held during the third and fourth month of this project. Development of the paired comparison worksheets can be completed during the first week of this task, regardless of data collection mode. At the beginning of the second week, we recommend sending the mail survey instrument to all panelists via Federal Express, following up with the panelists during the third week, and collecting completed instruments from late responders during the fourth week. If face-to-face meetings are held, they can commence starting the second week of this task.
Task 3: Collect and process the responses from the panelists
It is anticipated that collecting and processing the responses from the panelists should be completed within two weeks of the survey ending or the panel meetings concluding. A matrix of survey results on the likelihood of one code being preferred to another needs to be prepared for input into the Rasch software.
Task 4-6: Process the survey results through the Rasch software and convert to RVUs
The output from the Rasch software must be converted to work RVUs and tables developed displaying the current and predicted work RVUs generated from the Rasch software. Development of tabular presentation materials of these results should be doable within a two week time period.
Tasks 7-9: Identify misvalued services
It is anticipated that an additional four weeks would be spent identifying outlier codes from 0 the ratings obtained from the panelists and processed through the Rasch software. Individual codes or small families of codes should be determined to be aligned or misaligned and referred to the RUC for review as appropriate.
Task 10: Send to the RUC
The last step in this method is the submission of identified services to the RUC for the review and HCFA review of any proposed new work RVUs. A specific time frame for the RUC deliberations and HCFA review is not included in Exhibit 2-3 as it can vary depending upon the number of services submitted to the RUC, the number of specialties that need to be surveyed, and availability of RUC internal resources. In Chapter 3, we provide a more general discussion of the timing of these activities within the context of the next five year review.
2.2.9 References
Andrich, David, Rasch Model for Measurement, (Newbury Park: Sage University Paper 68, 1984)
Florin, Robert, "A Study of Relative Work Values for a Series of Laminectomy Codes Using a Technique Called Paired Comparisons," unpublished paper, March, 1998.
Florin, Robert, "Paired Comparisons: A Method for Ranking Physician Work," unpublished working paper, January, 1999.
Florin, Robert, "Report on the Study of General Surgery Key Reference Procedures by Paired Comparison of Work Values," memo to ACS Physician Reimbursement Committee, July 1, 1998.
Wright, Ben, "Fundamental Measurement in Social Science & Education, www.rasch.org/memo33a.htm, March 30, 1983.
Wright, Ben, "Fundamental Measurement for Outcome Evaluation," www.rasch.org/memo66.htm 1997.
Extracted from:
Five Year Review of Work Relative Value Units: Final
Report.
Section: The Identification of Potentially Misvalued Work
RVUs.
by Nancy T. McCall, Jerry Cromwell, and Michelle L. Griggs. June
15, 1999. Health Economics Research,
Inc.,
411 Waverley Oaks Road, Suite 330, Waltham MA 02452-8414,
(781)788-8100, FAX (781)788-8101
The research presented in this report was performed under Health Care Financing Administration (HCFA) Prime Contract No. 500-97-0443. Task Order No. 2004, Jim Menas, Project Officer. The statements contained in this report are solely those of the authors and no endorsement by HCFA should be inferred or implied.
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/florin.htm