Using the KeyFIM...

Instantaneous Measurement and Diagnosis

Presented at Outcome Measurements in Rehabilitation

by John Michael Linacre
MESA Psychometric Laboratory

Instantaneous measurement and diagnosis by means of observations on rating scales can be explained and demonstrated by means of a practical example: The KeyFIM - Self-Measuring Score Form.

The Functional Independence Measure (FIM^SM) is an observation instrument used to track the improvement of patients during rehabilitation. In its most widely distributed version, the instrument is merely a data collection form on which the ratings of the 18 FIM items are recorded. The data are then entered into a computer system and analyzed elsewhere and later. The clinical staff may never be informed of the results. With a redesigned form, however, data collection can immediately encompass measurement and fit diagnosis.

Comprehensive Rasch analysis of FIM data has been undertaken (see References). This has enabled the construction of a self-measuring version of the FIM, the KeyFIM. An abbreviated version, containing only the 5 cognitive items of the FIM is presented here.

The KeyFIM form is used for data collection, then measurement construction, and finally diagnostic analysis. First, the form is turned on its side for data collection. The rating given to each item is recorded, and the corresponding value circled on the pre-calibrated expected-score scale (obtained from a calibration run using normative data, and reported in BIGSTEPS Table 2.2). When extreme ratings are observed (1 and 7 in the KeyFIM), the circle extends from the printed extreme rating value to the edge of the active area.

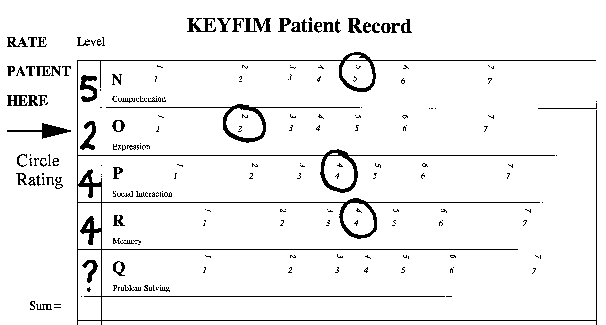
In clinical settings, different staff members rate different items. In this example, Item Q, "Problem Solving" has not yet been rated (and may never be).

Second, the form is used for measurement construction. Once some data has been recorded, the KeyFIM is rotated back to the vertical. A line is drawn across it, by eye, through the middle of the bulk of the ratings (ignoring outliers) to represent this patient's usual level of functioning. Looking across to the "FIM Raw Score" column, this patient's general level of performance corresponds to a FIM score of "21". We can also fill in a useful predicted rating value for unobserved item Q at "3". (Note that this would give a FIM sum-of-ratings score of 18. It is lower than the expected score of 21 because we ignored the outlying rating of "2" on item O, "Expression".)

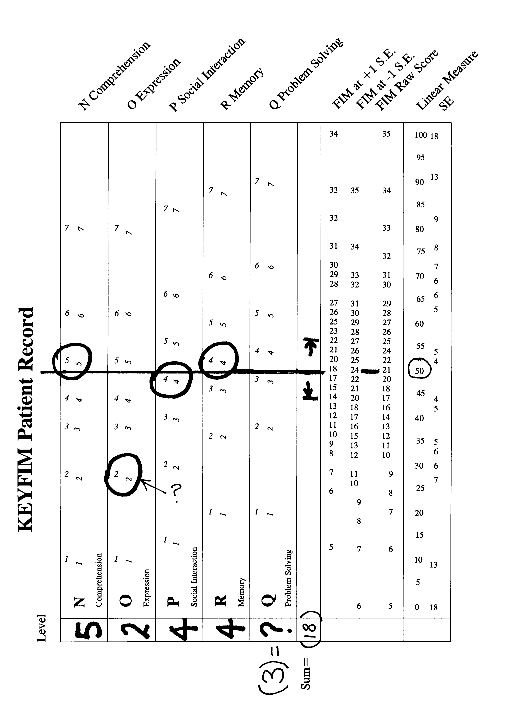
To the right can be seen a linear measure for this patient on a convenient logit rescaling from 0 to 100. 0 corresponds to the lowest meaningful logit measure on this instrument, 100 to the highest. The patient's measure is 50±6 measurement units (FIMITs). This S.E. is estimated by eye to be about 6 FIMITs, rather than the indicated "4", due to one unobserved rating and one misfitting rating. The measurement imprecision inherent in a complete set of ratings can be seen by locating the FIM raw score values in the columns marked "FIM at +1 S.E." and "FIM at -1 S.E." and "FIM Raw Score". These three locations indicate the FIM measure and ±1 S.E. relative to it.

Third, the KeyFIM is used to identify and diagnose unexpected response patterns. In this example, the patient's deficit in "Expression", Item O, is glaring, and would immediately attract clinicians' attention for substantive reasons. The imprecision of a single rating is about 15 FIMITs overall (and less than 10 FIMITs in the center of the scale). This rating is over 20 FIMITs less than the patient's typical level of performance and so it is also somewhat surprising on statistical grounds. The KeyFIM has now given as much guidance to the clinical staff, in seconds, as an elaborate computer analysis gives in months!

Self-measuring forms are simple to construct. Most of the effort goes into making them as helpful and convenient as possible for the users.

References:

Fisher A.G., Bryze K.A., Granger C.V., Haley S.M., Hamilton B.B., Heinemann A.W., Puderbaugh J.K., Linacre J.M., Ludlow L.H., McCabe M.A., Wright B.D. (1994) Applications of conjoint measurement to the development of functional assessments. International Journal of Educational Research 21(6) p.579-594

Granger C.V., Hamilton B.B., Linacre J.M. Heinemann A.W., Wright B.D. (1993) Performance profiles of the Functional Independence Measure. American Journal of Physical Medicine and Rehabilitation 72:2 April 84-89.

Heinemann A.W., Hamilton B., Linacre J.M., Wright B.D., Granger C.V. (1995) Functional status and therapeutic intensity during inpatient rehabilitation. American Journal of Physical Medicine and Rehabilitation. 74(4) p. 315-326.

Heinemann A.W., Linacre J.M., Wright B.D., Hamilton B., Granger C.V. (1994) Measurement characteristics of the Functional Independence Measure. Topics in Stroke Rehabilitation 1(3) p.1-15. Fall.

Linacre J.M., Heinemann A.W., Wright B.D., Granger C.V., Hamilton B.D. (1994) The structure and stability of the Functional Independence Measure. Archives of Physical Medicine and Rehabilitation 75(2), 127-132, Feb.

Linacre J.M., Wright B.D. (1991) BIGSTEPS Rasch Analysis Computer Program. Chicago IL: MESA Press.

Linacre J.M., Wright B.D., Heinemann A., Hamilton B. (1991) Criterion-sensitive measurement. Paper presented at AERA Annual Meeting. April. Chicago. (ERIC ED 333 048)

Wright B.D., Linacre J.M., Heinemann A.W. (1993) Measuring functional status in rehabilitation. Physical Medicine and Rehabilitation Clinics of North America 4(3) 475-491. August.

This appeared in
Physical Medicine and Rehabilitation
11 (2) pp. 315-324, June 1997

Go to Top of Page
Go to Institute for Objective Measurement Page

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	Journal of Applied Measurement
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

FORUM

Rasch Measurement Forum to discuss any Rasch-related topic

Our current URL is www.rasch.org

The URL of this page is www.rasch.org/memo60.htm