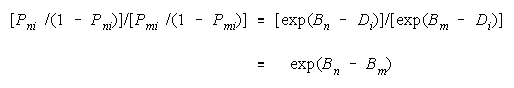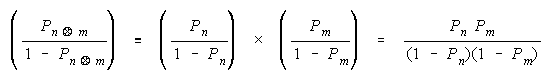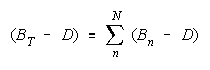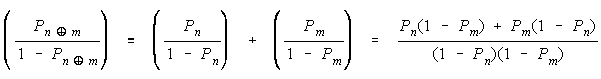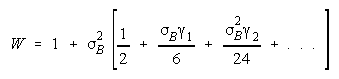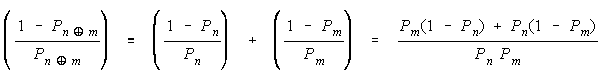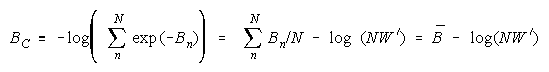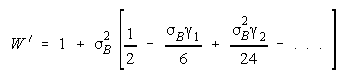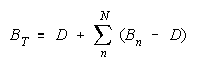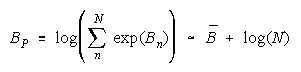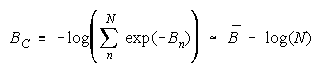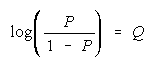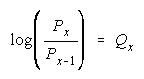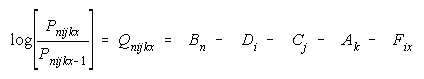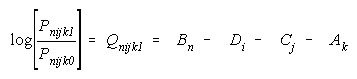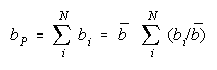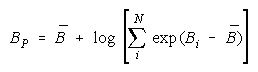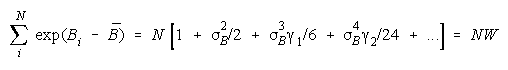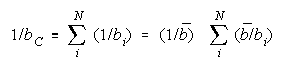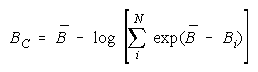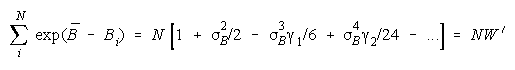Composition Analysis: Teams, Packs, Chains
Bookstein's deductions that any distribution function reducing to
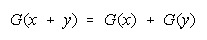
or
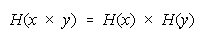
will be resilient to
aggregation ambiguity is applied to performance odds. The Rasch model and three measurable
compositions result. TEAMs work as unions of perfect agreement doing best with easy problems.
PACKs work as collections of perfect DISagreements doing best with intermediate and hard problems.
CHAINs work as connections of IMperfect agreements doing better than TEAMs with hard problems.
Four problem/solution necessities for inference are reviewed: uncertainty met by probability, distortion
met by additivity, confusion met by separability and ambiguity met by divisibility. Connotations,
properties and applications of TEAM, PACK and CHAIN groups are ventured.
INTRODUCTION
Why do some organizations succeed while others fail? Why do groups of a particular kind work
well in some situations but poorly in others? The psychology of group organization is rich but
qualitative (Freud, 1921). Questions about how groups work seem non-mathematical. Nevertheless,
algebra undertaken to obtain hierarchically stable measurement leads to a mathematics of group
productivity.
Groups are composed of subgroups, subgroups of elements, elements of parts. Aggregations
separate into sub-aggregations and come together into super-aggregations. The "entities" we experience
become understood and useful as we learn how to see down into their substructures and up into the
compositions they construct.
We know from experience that the way group members work together affects group success.
But we do not know how to measure these effects, nor how to calculate effective group organizations.
Quantification requires models which measure group strength as functions of member strengths. These
models must be hierarchically robust. They must maintain their metric across descending and ascending
levels of composition. Can a mathematics be developed which defines the different ways group
members might work together such that their individual measures can be combined mathematically to
calculate an expected measure for the group?
COMPOSITION ANALYSIS
"Composition analysis" is our name for the mathematics of how component measures combine
to produce composite measures. Our deliberations will lead to measurement models which are infinitely
divisible and, hence, inferentially stable. The models will compose and decompose smoothly from one
level of aggregation to another. When the models work for groups of individuals, they will work for
individuals within groups. When they work for individuals, they will work for parts within individuals.
Although presented here as groups of persons, these models apply to groups of any kind: ideas,
problems, cells.
COMPOSITION RULES.
Bookstein (see Appendix) shows that any distribution function that reduces to

or
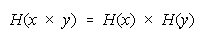
will be indifferent to the intervals used for grouping and hence resilient to aggregation ambiguity.
Bookstein's functions specify the divisibility needed for composition analysis. They also specify the
arithmetic needed for quantitative comparisons. To relate these functions to the procedures of
measurement, we enlarge the + and x arithmetic inside functions G and H to include "procedural"
compositors
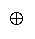
and

. These procedural "additions" and "multiplications" represent whatever
empirical procedures are discovered to operationalize measurement, as in "aligning sticks end-to-end" to
"add" length, and "piling bricks top-to-bottom" to "add" weight.
Two composition rules follow:
A Procedural Addition rule:
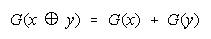
A Procedural Multiplication rule:
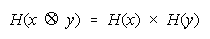
These rules compose and decompose ad infinitum, as in:

To discover the consequences for composition analysis, we will apply each rule to observation
probabilities. Observation probabilities are addressed we intend to use these rules on data in order to
estimate measures for empirical compositions. These probabilities will be expressed as odds because
0 < P < 1 is an awkward measure while 0 < [P/(1 - P)] < maintains equal ratios and loge odds maintain
equal differences. Our application of Bookstein's functions to odds will determine what compositions
compositors
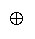
and
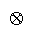
imply and hence what compositions are quantifiable.
Three compositions will result:
1. a TEAM union of perfect agreement,
2. a PACK collection of helpful DISagreements and
3. a CHAIN connection of IMperfect agreements.
We will deduce measurement models for these compositions, which, because of their divisibility,
are indifferent to composition level and resilient to aggregation ambiguity. The resulting models will be
the stable laws of composition analysis.
Finally we will place divisibility in the theory of inference which motivates these deductions and
venture some interpretations of the three compositions.
THE MEASUREMENT MODEL
In order to apply the composition rules, we need a stochastic measurement model with
parameters that follow the rules of arithmetic and estimates that enable comparisons between strengths
Bn and Bm of objects n and m which are invariant with respect to whatever relevant, but necessarily
incidental, measuring agents are used to manifest the comparison.
Measurement means quantitative comparison. Quantitative comparison means differences or
ratios. Since odds are ratios, ratios are their comparison. The procedural comparison
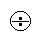
of objects
n and m is:
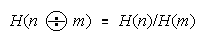
Defining H as odds [P/(1 - P)] gets:

Estimation requires that strengths Bn and Bm be manifest by a relevant measuring agent i of
difficulty Di. Inferential stability requires that the comparison (Bn - Bm) be independent of task difficulty
Di.
The necessary and sufficient model is:
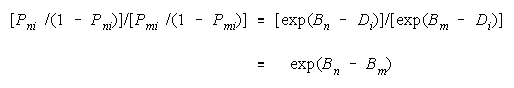
because task difficulty Di cancels so that the n
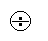
m comparison maintains the same difference of
strengths regardless of which tasks are convenient to manifest these strengths (Rasch, 1960).
THREE COMPOSITIONS
TEAM UNION OF PERFECT AGREEMENT.
Applying procedural multiplication to success odds defines group success odds, when group
members work according to the procedural operator
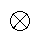
as the following product of group member success odds:
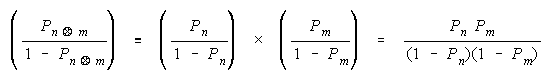
The group composition specified by this first law of stable measurement can be seen by applying
probabilities Pn and Pm to the outcomes possible when persons n and m work on a task according to the
multiplication of their success odds. Figure 1 shows the two outcomes which occur in this composition.
Figure 1.
Outcomes Occurring for a TEAM.
|
m loses
0 |
m wins
1 |
n loses
0 |
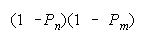
TEAM 00 loses |
Disagreement
Absent |
n wins
1 |
Disagreement
Absent |
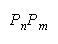
TEAM 11 wins |
Agreement (11) wins or agreement (00) loses. Disagreements (10) and (01) are absent because
they do not occur in the equation which defines TEAM composition. TEAMs work as unions of perfect
agreement.
Applying Rasch odds to TEAM work with group strength represented by
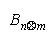
gets:
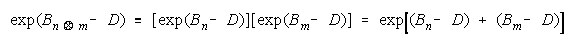
Taking logs and generalizing to any size group defines N-member TEAM strength as:
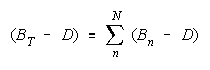
The strengths of TEAM members, relative to task difficulty (Bn - D), add up to TEAM strength, relative
to task difficulty (BT - D). TEAMs are concatenations of relative strengths, accumulated in linear form.
PACK COLLECTION OF PERFECT DISAGREEMENTS.
Applying procedural addition to success odds defines group success odds, when group members
work according to the procedural operator
as the following addition of group member success
odds:
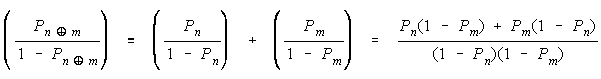
The group composition specified by this second law of stable measurement can be seen by
applying probabilities Pn and Pm to the outcomes possible when persons n and m work on a task
according to the addition of their success odds. Figure 2 shows the three outcomes which occur in this
composition.
Figure 2.
Outcomes Occurring for a PACK.
|
m loses
0 |
m wins
1 |
n loses
0 |

PACK 00 loses |
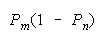
PACK 0 1 wins |
n wins
1 |
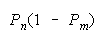
PACK 1 0 wins |
Agreement
Absent |
Helpful disagreements (10) and (01) win. Unhelpful disagreement (00) loses. Agreement (11)
is absent because it does not occur in the equation which defines PACK composition. PACKs work as
collections of perfect DISagreements.
Applying Rasch success odds to PACK work gets:
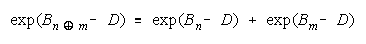
or

This is also a concatenation, but of absolute (not relative to problem difficulty) strengths, accumulated
in exponential form.
Taking logs and extending to a group of any size defines N-member PACK strength BP as:

with
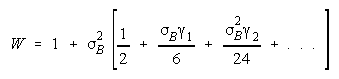
Loge (NW) is the amount PACK strength increases with PACK size N and member heterogeneity
W. W brings in member heterogeneity through member strength variance B2, skew:

kurtosis:
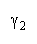
Positive skew and kurtosis amplify the impact of stronger PACK members.
The homeostasis of most groups induces homogeneity. When heterogeneity emerges, members
regroup toward homogeneity. As long as member strength variance B2 stays small, so that B<.3 for
1< W <1.1 or B<.5 for 1<W<1.2, then PACK strength can be modelled as:
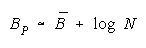
The perfect disagreements of PACK members collect to benefit the PACK. As PACK size
increases so does PACK strength. Unlike TEAMs, PACK strength is independent of task difficulty.
CHAIN CONNECTIONS OF IMPERFECT AGREEMENTS.
Applying procedural addition to failure odds defines group failure odds, when group members
work according to the procedural operator
as the following addition of group member failure
odds:
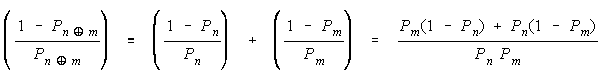
The group composition specified by this third law of stable measurement can be seen by
applying probabilities Pn and Pm to the outcomes possible when persons n and m work on a task together
according to the addition of their failure odds. Figure 3 shows the three outcomes which occur in this
composition.
Figure 3.
Outcomes Occurring for a CHAIN.
|
m loses
0 |
m wins
1 |
n loses
0 |
More than one loss
Absent |
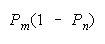
CHAIN 0 1 loses |
n wins
1 |
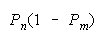
CHAIN 1 0 loses |
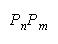
CHAIN 11 wins |
Perfect agreement (11) wins. Disagreements (10) or (01) lose. Outcome (00) is absent because
it does not occur in the equation that defines CHAIN composition. CHAINs work as connections of
IMperfect agreements.
Applying Rasch failure odds to CHAIN work gets:

or
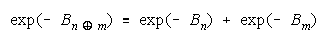
a concatenation of absolute weaknesses in exponential form.
Taking logs and extending to a group of any size defines N-member CHAIN strength BC as:
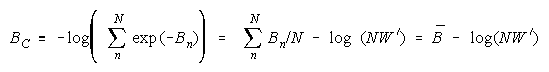
with
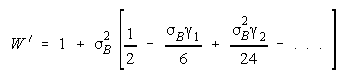
which member homogeneity simplifies to:
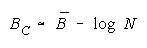
The imperfect agreements of CHAIN members are connect against the danger of harmful
disagreement. Like PACKs, CHAIN strength is independent of problem difficulty. Unlike PACKs, as
CHAIN size increases, CHAIN strength decreases.
COMPARING COMPOSITIONS
To see the differences among TEAMs, PACKs and CHAINs consider the possibilities for groups
of three in Figure 4 and for groups of any size in Figure 5.
Figure 4.
Outcomes for Three Member Groups.
|
TEAM |
|
PACK |
CHAIN |
| WIN |
Agreement
111 |
|
Helpful
Disagreement
100,010,001 |
Agreement
111 |
|
LOSE |
Agreement
000 |
|
Disagreement
000 |
Harmful
Disagreement
011,101,110 |
|
|
|
|
|
| ABSENT |
100,010,001
110,101,011 |
|
111
110,101,011 |
000
100,010,001 |
Figure 5.
Outcomes for Any Size Group.
|
AGREE |
DISAGREE |
| WINS |
TEAM
all 1's |
PACK
a single 1 |
| LOSES |
TEAM
all 0's |
CHAIN
a single 0 |
or
|
TEAM |
PACK |
CHAIN |
| all 1's |
WINS |
*** |
WINS |
both
0's & 1's |
***
*** |
One 1
WINS |
One 0
loses |
| all 0's |
loses |
loses |
*** |
*** Absent
TEAMs are united in perfect agreement. Win or lose, no disagreement can occur. PACKs and
CHAINs distinguish disagreement, but conversely. PACKs win by a single winning disagreement.
CHAINs lose by a single losing disagreement.
To help a TEAM, a member's strength must be stronger than problem difficulty. Members weaker than
problem difficulty decrease TEAM strength. Adding to a PACK increases PACK strength. Adding to a
CHAIN decreases CHAIN strength.
The measurement models for composition analysis in Figure 6 enable us to deduce which of
these compositions works best against problems of different difficulties.
Figure 6.
Measurement Models for Composition Analysis.
TEAMs:
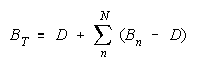
Bn > D helps
Bn < D hurts
PACKs:
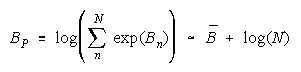
more N helps
CHAINs:
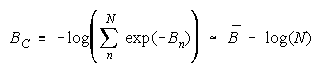
more N hurts
TEAMs vs PACKs. When is one united TEAM agreement on what is best more effective than a
collection of PACK disagreements?
Since
BT = BP when
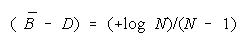
BT > BP requires
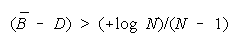
TEAMs do better than PACKs when average group strength is greater than problem difficulty by
[(+loge N)/(N - 1)]. This defines the upper curve in Figure 7.
TEAMs vs CHAINs. When is TEAM organization better than CHAIN organization?
Since
BT = BC when
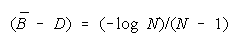
BT > BC requires
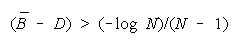
This is the lower curve in Figure 7.
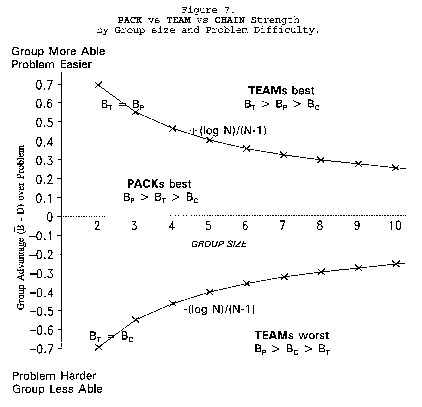
To read Figure 7, find group size N = 4 on the horizontal axis. Go up to the upper curve and left
to the vertical axis to read that a group of four must average half a logit more strength than problem
difficulty to do better as a TEAM than a PACK.
When problem D is harder than
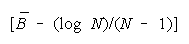
PACK disagreement is more
productive than TEAM agreement. As problem difficulty (D - B) increases, the value of TEAM work
declines. The turning point at which PACKs become better than TEAMs is always greater than zero.
Below (B - D) = (-loge N)/(N - 1), a TEAM becomes the least productive group organization. Figure 8
formulates the relative strengths of TEAMs, PACKs and CHAINs.
Figure 8.
Relative Strengths of TEAMs, PACKs and CHAINs.
WHEN: THEN:
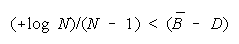
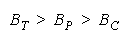
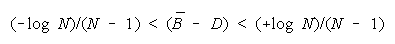
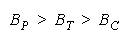
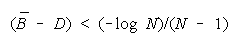
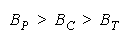
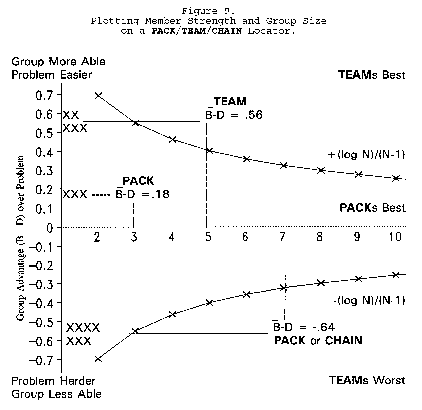
Figure 9 uses Figure 7 to show how relationships between problem difficulty, group size and
group organization can be used to design optimal work groups. The upper group of five, averaging .56
logits more able than their problem, should work best in TEAM agreement. The middle group of three,
averaging only .18 logits more able than their problem, should work better in PACK disagreement. The
bottom group of seven, averaging .64 less able than their problem, however, encounter an additional
consideration. Optimal organization for this group depends on the cost/benefit balance between success
and failure. When opportunity invites, PACK disagreements should be more productive. When danger
looms, however, CHAIN commitment to maintain agreement may be safer.
VISUALIZING GROUP MIXTURES. When empirical measures BG are estimated from group
performance, we can see where each BG fits on the line of TEAM, PACK and CHAIN compositions
implied by its member measures {Bn for n = 1,N} by plotting BG at:
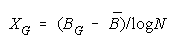
and
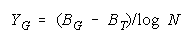
in an XY-plot benchmarked by a TEAM, PACK, CHAIN line with intercept (AND, 0), slope one and
composition reference points:
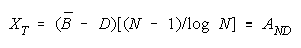

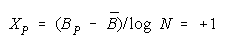
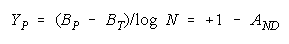
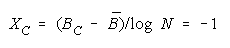
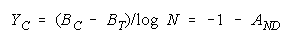
GENERALIZING THE MEASUREMENT MODEL
To expand probability

in Q, write its log
odds
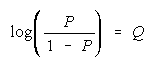
Subscripting P and (1-P) to P1 and P0 for

leads to
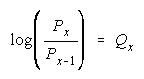
a Rasch model for any
number of ordered steps: x = 1, 2, 3, , , m-1, m, ... , . This
model constructs additive conjoint measurement from data obtained
through any orderable categories: dichotomies, ratings, grades,
partial credits (indexing xi and Qix to item i), comparisons,
ranks, counts, proportions, percents...
We can use this model to articulate a variety of frequently
encountered facets. To represent a measure for person n, we
introduce person parameter Bn. To produce an observable response
xni, we provoke person n with item i designed to elicit
manifestations of the intended variable. To calibrate item i,
and so construct a quantitative definition of the variable, we
introduce item parameter Di. To calibrate the resistance against
moving up in item i from category x-1 to x, we add item step
parameter Fix. With Di and Fix in place, we can estimate test-free
person measures which, for data which follow the model, are
stable with respect to item selection.
When person n responds directly to item i, producing
response xni, we can collect xni's over persons and items and
construct person measures on the item-defined variable. But,
when persons are observed through performances which are not
self-scoring, then we need a rater j to obtain rating xnij of
person n's performance on item i. But we know that even the best
trained raters vary in the way they use rating scales. To
calibrate raters, we add rater parameter Cj. With Cj in place,
we can estimate rater-free, as well as test-free, person measures
which, for data that fit, will be stable with respect to rater
selection as well as item selection.
As comprehension of the measurement context grows, we can
add more facets, a task parameter Ak for the difficulty of the
task on which person n's performance is rated by rater j on item
i to produce xnijk and so on.
In order to obtain inferential stability [Fisher sufficiency
(1920), Thurstone invariance (1925), a stochastic Guttman scale
(1944), Rasch objectivity (1960), and Luce and Tukey conjoint
additivity (1964)] we need only combine these parameters
additively into a many-facet model (Linacre, 1989) such as:
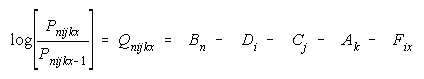
where Bn is the person parameter, Di is the item parameter, Cj is
the rater parameter, Ak is the task parameter and Fix is the item
step parameter.
Compositions can be studied in any facet of a many-facet
model. Consider:
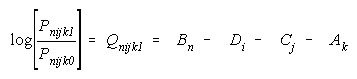
rewritten for x = 0,1 to simplify presentation. The measurement
models for TEAMs of animate elements, persons and raters, and for
BLOCKs of inanimate elements, items and tasks, are listed in
Figure 10.
Figure 10.
Facet Measures for TEAMs and BLOCKs.
Group Type Measurement Model
Person TEAM n = 1,...,N
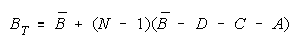
Item BLOCK i = 1,...,L

Rater TEAM j = 1,...,M

Task BLOCK k = 1,...,H
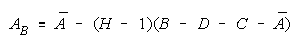
For TEAM and BLOCK measures to increase with group size, the
average measure of the grouped facet must exceed:

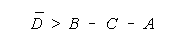
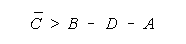
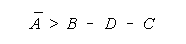
The PACK and CHAIN formulations in Figure 11 are simpler.
For PACKs and CHAINs the levels of other facets do not matter.
More persons make person PACKs stronger, but person CHAINs
weaker. More items, raters or tasks make PACKs easier to
satisfy, but CHAINs more difficult.
Figure 11.
Facet Measures for Homogeneous PACKs and CHAINs.
PACKs CHAINs
Persons


Items

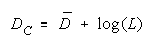
Raters

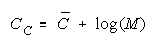
Tasks

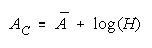
NECESSITIES FOR INFERENCE
Four problems interfere with inference:
Uncertainty is the motivation for inference. We have only
the past by which to infer the uncertain future. Our solution is
to contain uncertainty in probability distributions which
regularize the irregularities that disrupt connections between
what seems certain now but must be uncertain later.
Distortion interferes with the transition from data
collection to meaning representation. Our ability to figure out
comes from our faculty to visualize. Visualization evolved from
the survival value of safe body navigation. Our solution to
distortion is to represent data in bilinear forms that make the
data look like the space in front of us. To "see" what
experience "means", we "map" it.
Confusion is caused by interdependency. As we look for
tomorrow's probabilities in yesterday's lessons, interactions
intrude and confuse us. Our solution is to force the
complexities of experience into few enough invented "dimensions"
to make room for clear thinking. The authority of these fictions
is their utility. We will never know their "truth". But, when
our fictions "work", they are usually useful.
The logic we use to control confusion is enforced
singularity. We investigate the possibilities for, define and
measure one dimension at a time. The necessary mathematics is
parameter separability. Models which introduce putative "causes"
as separately estimable parameters are the founding laws of
quantification. They define measurement. They determine what is
measurable. They decide which data are useful, and which are
not.
Ambiguity is the fourth problem for inference. We control
hierarchical ambiguity by using measurement models which embody
divisibility.
Bookstein's functions:

and

for resilience to aggregation ambiguity contain the divisibility
necessary to stabilize quantitative inference (Feller, 1966).
They also contain the parameter separability and linearity
necessary to alleviate confusion and distortion. Models which
follow from Bookstein's functions implement:
1. the concatenation and conjoint additivity which Norman
Campbell (1920) and Luce and Tukey (1964) require for
fundamental measurement,
2. the exponential linearity which Ronald Fisher (1920)
requires for estimation sufficiency and
3. the parameter separability which Thurstone (1925) and
Rasch (1960) requires for objectivity.
The measurable compositions are TEAMs, PACKs and CHAINs.
The measurement models necessary and sufficient for quantitative
composition analysis are linear mixtures of the Rasch models for
measuring these compositions. Figure 12 summarizes the problems
of inference and their current.
Figure 12.
Foundations of Inference.
| PROBLEMS |
SOLUTIONS |
PARENTS |
UNCERTAINTY
have want
now later
statistic parameter |
PROBABILITY
distribution
regular irregularity
misfit detection |
Bernoulli 1713
De Moivre 1733
Laplace 1774
Poisson 1837 |
DISTORTION
non-linearity
unequal intervals
incommensurability |
ADDITIVITY
linearity
arithmetic
concatenation |
Luce/Tukey 1964
Fechner 1860
Helmholtz 1887
N.Campbell 1920 |
CONFUSION
interdependence
interaction
confounding |
SEPARABILITY
sufficiency
invariance
conjoint order |
Rasch 1960
R.A.Fisher 1920
Thurstone 1925
Guttman 1944 |
AMBIGUITY
arbitrary grouping
ambiguous hierarchy |
DIVISIBILITY
independence
stability
reproducibility
exchangeability |
Kolmogorov 1932
Levy 1924
Bookstein 1992
de Finetti 1931 |
For Bernoulli, De Moivre, Laplace and Poisson see Stigler (1986).
For Kolmogorov and Levy see Feller (1966).
The prevalence, history and logic of the addition and
multiplication rules establish Rasch measurement models as the
necessary and sufficient foundations for measurement. Models
which contradict the inferential necessities of: probability,
linearity, separability and divisibility, cannot survive the
vicissitudes of practice. Only data which can be understood and
organized to fit a Rasch model can be useful for constructing
measures.
CONNOTATIONS, PROPERTIES AND STORIES
Mathematics leads to three reference compositions which
empirical composites must mix to be measurable. We can use group
member measures to calculate TEAM, PACK and CHAIN expectations.
We can use these expectations and empirical group measures to
study TEAM/PACK/CHAIN mixtures. So much for mathematics. What
can TEAMs, PACKs and CHAINs say about everyday life? How might
we bring these mathematical ideas to practice as useful
formulations for better living? Can these abstractions help us
manage our infinitely complex experiences with living
compositions, hierarchies of functioning, families of ideas and
tasks? Can we construct maps by which to "see" how the
compositions of which we are, by which we think and within which
we live, might be better worked? Figure 13 lists some
connotations which TEAMs, PACKs and CHAINs bring to mind. Figure
14 lists some properties which they imply. We end with some
stories in which these compositions might participate.
Figure 13.
Connotations of TEAM, PACK and CHAIN.
|
SAFE
SURE |
DANGEROUS
UNSURE |
|
AGREE |
TEAM
government
formality
convention |
CHAIN
survival
security
discretion |
|
DISAGREE |
PACK
science
opportunity
invention |
chaos
anarchy
|
|
TEAM |
PACK |
CHAIN |
|
WIN |
virtue
satisfaction
justice |
pride
triumph
progress |
safety
relief
security |
|
LOSE |
guilt
indignation
worry |
shame
frustration
disappointment |
fear
recrimination
despair |
Football. When a TEAM of players huddle to call a play, win or
lose, they intend to act united. Should one of them err, he will
hurt the TEAM. TEAM success is jeopardized by weak links in its
CHAIN of players.
Lost Keys. What is the best way to look for a lost key? Should
we all agree to look in the same place? Or, should we all agree
to disagree as to where to look and spread out?. Each in a
different place has the better chance of success. PACK work is
the way to look for lost keys.
Mountain Climbing. Climbers rope for safety. As one climbs,
everyone else hangs on. Then, should a climber slip, his
anchored mates may be able to save him. When, however, a
supposedly anchored mate is not hanging on or moves out of turn,
then all may fall. CHAIN work is the way to climb mountains.
Cops and Robbers. When a crime is reported, the perpetrator is
often unknown. Solving the problem begins hard. PACKs of
detective TEAMs fan out to search of suspects. As evidence
accumulates, however, deciding who's guilty becomes easier. The
PACK of TEAMs converges in their solutions to one TEAM agreement
and detains the most likely suspect.
Should the suspect go to trial, judgement will depend on a
jury TEAM decision. But, if a contrary jurist holds out, the
jury TEAM may become a failing CHAIN.
Figure 14.
Properties Implied by TEAM, PACK and CHAIN.
| TEAM |
PACK |
CHAIN |
| unite |
collect |
connect |
| consolidate |
accumulate |
protect |
| evaluate |
explore |
preserve |
| unify |
discover |
secure |
| agree |
attack |
defend |
uphold
ground |
gain
ground |
guard
ground |
capitalize
consensus |
optimize
difference |
survive
together |
| play safe |
take chance |
hang on |
smug
secure |
daring
hopeful |
cautious
worried |
virtue
disapproval |
pride
shame |
safety
danger |
usual
events |
rare
events |
dangerous
events |
easy
problems |
hard
problems |
risky
problems |
successful
jury |
missing
key |
mountain
climbing |
A Common Source of Misapprehension. A weak shooter, in solitude,
misses repeatedly. But then, in sudden company, is seen to hit on
what is now his Nth try. His PACK ability:
BPN = B + loge N => BP1 = B' + loge 1 = B', when only his finally
successful shot is seen, will appear to be the ability B' of a
stronger shooter who hits on his first try.
A strong shooter, in solitude, hits repeatedly. But then, in
sudden company, is seen to miss on what is now her Nth try. Her
CHAIN ability: BCN = B - loge N => BC1 = B" - loge 1 = B" , when only
her finally unsuccessful shot is seen, will appear to be the
ability B" of a weaker shooter who misses on her first try.
Solving Problems. When problems are easy, TEAMing ideas into one
course of action should work best. When problems are hard,
however, putting every egg in a single basket may not be as
productive as deploying a PACK of diverse undertakings. When a
mistake is fatal, however, then PACK diversity risks CHAIN
weakness.
MESA Memorandum 67, 1994
Benjamin D. Wright
MESA Psychometric Laboratory
REFERENCES
Bookstein, A. (1992). Informetric Distributions, Parts I and II, Journal of the American Society for Information Science,
41(5):368-88.
Campbell, N.R. (1920). Physics: The elements. London: Cambridge University Press.
de Finetti, B. (1931). Funzione caratteristica di un fenomeno aleatorio.
Atti dell R. Academia Nazionale dei Lincei, Serie 6. Memorie, Classe di
Scienze Fisiche, Mathematice e Naturale, 4, 251-99.
[added 2005, courtesy of George Karabatsos]
Fechner, G.T. (1860). Elemente der psychophysik. Leipzig: Breitkopf & Hartel. [Translation: Adler, H.E. (1966). Elements
of Psychophysics. New York: Holt, Rinehart & Winston.].
Feller, W. (1966). An introduction to probability theory and its applications, Volume II. New York: John Wiley.
Fisher, R.A. (1920). A mathematical examination of the methods of determining the accuracy of an observation by the mean
error and by the mean square error. Monthly Notices of the
Royal Astronomical Society,(53),758-770.
Freud, S. (1921). Group psychology and the analysis of the ego.
New York: Norton.
Guttman, L. (1944). A basis for scaling quantitative data.
American Sociological Review,(9),139-150.
Helmholtz, H.V. (1887). Zahlen und Messen erkenntnis-theoretisch betrachet. Philosophische Aufsatze Eduard Zeller gewidmet.
Leipzig. [Translation: Bryan, C.L. (1930). Counting and
measuring. Princeton: van Nostrand.].
Linacre, J.M. (1989). Many-facet Rasch measurement.
Chicago: MESA Press.
Luce, R.D. & Tukey, J.W. (1964). Simultaneous conjoint measurement.
Journal of
Mathematical
Psychology,(1),1-27.
Rasch, G. (1960). Probabilistic models for some intelligence and attainment tests. [Danish Institute of Educational Research
1960, University of Chicago Press 1980, MESA Press 1993]
Chicago: MESA Press.
Stigler, S.M. (1986). The history of statistics. Cambridge: Harvard University Press.
Thurstone, L.L. (1925). A method of scaling psychological and educational tests. Journal of Educational Psychology,(16),
433-451.
APPENDIX
Properties of Robust Functions
A. Bookstein, University of Chicago
INTRODUCTION
The concern of this appendix is our ability to observe and
describe regularities in the face of ambiguity. Since much of
Social Science data are based on ill-defined concepts, this ability
has serious practical implications.
Policy decisions are often based on assumptions about how
certain characteristics are distributed over an affected
population. Such assumptions tend to be expressed in terms of
functions describing statistical distributions. Although these
functions critically influence our decisions, they are usually
created ad hoc, with little or no theoretic support. We are
interested in situations in which the particular values entering
the function could be quite different, given a plausible
redefinition of the concepts being probed. In such situations, it
is reasonable to demand of the functions involved, that reasonable
redefinition of key concepts not result in new functions that
change the decisions being made.
We examined one case in which counts were described in terms
of an unknown function, f(x) (Bookstein, 1992). We had a
population of items, each with an associated latent parameter, x,
indicating its potential for producing some yield over a period of
time. The number of items with values of x between x0 and x0 +
is given by f(x)*. It is convenient to let f(x) = A*h(x), with
h(x) defined so h(1)=1.
The function, h(x) is unknown, but we would like the form that
it takes not to depend on the size of the interval chosen.
Demanding this constraint led to the condition that h(x) must obey:
h(xy)=h(x)h(y). This functional constraint in many cases
determines the function itself. For example, for h(x) a "smooth"
function, only the form h(x)= A/x is permitted.
The functional constraint, h(xy)=h(x)h(y), also resulted from
examining a wide range of other ambiguities in counting. Similar
requirements occur in other contexts. In an interesting and
important example, Shannon, in defining the properties of a measure
of information, first considers the uncertainty of which of M
equally likely events will occur. He argues that, if this is given
by a function f(M), this function must obey f(MN) = f(M) + f(N).
A discussion of the consequences of this assumption is found in Ash
(1965).
In the example of information, a transition is made between
discrete counts and continuous variables, the probabilities of
events. But the constraint also plays a critical role in number
theory, where a number of key "number theoretic" functions have a
similar property (though it is usually assumed that the values
corresponding to M and N are relatively prime.) For example, the
function (n) giving the number of integer divisors of an integer
n satisfies this condition. An excellent treatment of number
theoretic functions from this point of view may be found in Stewart
(1952).
Thus we find that the constraint is both strong, in the sense
of determining the form of the functions satisfying it, and
widespread. Both information and counts are central to much of
Social Science policy making. It is the purpose of this appendix
to show that other types of commonly occurring constraints are
simply related to the one given above.
OTHER FORMS
The previous section defined a key relation that it is
attractive for our functions to obey h(xy)=h(x)h(y). Given such
a function, we can define other functions with interesting
functional properties. For example, k(x) = loge(h(exp(x))). Using
the properties of loge, h, and exp, it is easy to see that k obeys
k(x+y) = k(x) + k(y). Similarly, given such a function k(x), we
could define a function h(x) = exp(k(loge(x))) which obeys the
initial condition.
EVALUATING k(x)
We have some freedom in evaluating k(x), but not much. We can
now list some consequences of the constraint.
1. We immediately see that, if k(x) satisfies the additivity
condition, so does A*k(x), for any constant A. This allows us
to choose k for which: k(1) = 1.
2. But if so, we can evaluate k(1/m), for any integer m,
1= k(1) = k({1/m + 1/m + ... + 1/m}m) = m*k(1/m), so,
k(1/m) = 1/m.
3. Similarly, k(mx) = m*k(x), so given any positive rational
number, m/n, we have, k(m/n)= mk(1/n) = m/n.
4. Since k(x) = k(x+0) = k(x) + k(0), we must necessarily
have, k(0) =0.
5. Also, since 0 = k(0) = k(x + (-x) ) = k(x) + k(-x), we can
conclude that, k(-x) = -k(x), for arbitrary x.
Thus we see that the additivity condition strictly imposes
values that k can take on the rational numbers, a set dense in the
real number line. If k(x) is smooth, then, in general, we must
have k(x) = Ax.
We can make a stronger statement: If k(x) is monotonic, say
monotonically increasing, in any interval I, no matter how small,
then it must be continuous in that interval and throughout its
range. Thus, k(x) = Ax. For suppose k(x) is monotonic in a small
interval including the irrational value x0. Then we can find
rational numbers r1 and r2, also in I, for which r1 < x0 < r2. Thus,
we have k(r1) < k(x0) < k(r2). This is true even if we choose a
sequence of r1 and r2 increasingly close to x0. For such values,
k(r1) = r1 and k(r2) = r2 both approach x0, so k(x0) must itself
equal x0. Thus, at least in I, k(x) = x, for irrational as well as
rational x.
But now consider any x. Certainly k(x) = k(r+(x-r)) =
r+k(x-r), for r a rational number near enough to x that there
exist values x1 and x2, both in I for which x1 - x2 = x - r. Then,
k(x-r) = k(x1 - x2) = k(x1) - k(x2). But in this interval, we saw
k(x)=x. Thus we have k(x) = r + x1 - x2 = r + (x - r) = x, as it
was intended to prove.
REFERENCES
Ash, R. (1965) Information Theory, New York: Wiley.
Bookstein, A. (1992) Informetric Distributions, Parts I and II, Journal of the American Society for Information Science,
41(5):368-88.
Stewart, B.M. (1952) Theory of Numbers, New York: MacMillan.
DERIVATION for pages 5 and 7 of COMPOSITION ANALYSIS by
Benjamin Drake Wright
Derivation of PACK and CHAIN measure approximations from their
exponential (ratio) parameter definition.
PACK definition:
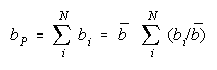
where
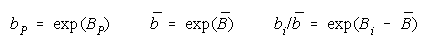
so that
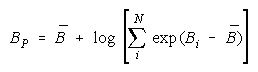
Since
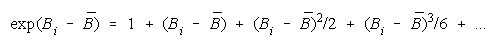
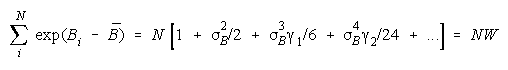
PACK measure becomes
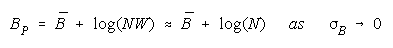
CHAIN definition:
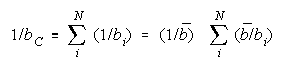
so that
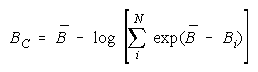
Since
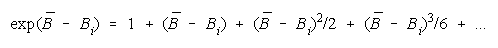
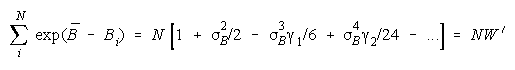
CHAIN measure becomes
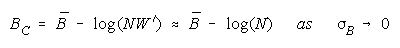
Go to Top of Page
Go to Institute for Objective Measurement Page
| Rasch-Related Resources: Rasch Measurement YouTube Channel |
|---|
Rasch Measurement Transactions &
Rasch Measurement research papers - free |
An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse |
Rasch Measurement Theory Analysis in R, Wind, Hua |
Applying the Rasch Model in Social Sciences Using R, Lamprianou |
El modelo métrico de Rasch:
Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition),
Manuel González-Montesinos M. |
| Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar |
Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
Rasch Models for Measurement, David Andrich |
Constructing Measures, Mark Wilson |
Best Test Design - free, Wright & Stone
Rating Scale Analysis - free, Wright & Masters |
| Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias |
Diseño de Mejores Pruebas - free, Spanish Best Test Design |
A Course in Rasch Measurement Theory, Andrich, Marais |
Rasch Models in Health, Christensen, Kreiner, Mesba |
Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen |
| Rasch Books and Publications: Winsteps and Facets |
|---|
| Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene |
Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver |
Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone |
Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale |
Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland |
| Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes |
Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang |
Statistical Analyses for Language Testers (Facets), Rita Green |
Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind |
Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M |
| Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind |
Rasch Measurement: Applications, Khine |
Winsteps Tutorials - free
Facets Tutorials - free |
Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre |
Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan |
| Rasch Meta-Metres of Growth for Some Intelligence and Attainment Tests: A Meta-metre for some Intelligence and Attainment Tests, David Andrich, Ida Marais, Sonia Sappl |
|
|
|
|
| Coming Rasch-related Events |
|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/memo67.htm