Explorations into Local Independence with T-Rasch

T-Rasch is a computer program that evaluates the conformance of dichotomous data to the local independence axiom of the Rasch model. This analysis yields insights into what is meant by "fit" to the model.

An example data file, Example1.dat, is provided with the Demo version of T-Rasch. This is shown as a Guttman scalogram in the Table. Item 8 is the easiest item, item 2 the hardest. "+"s flag the item and person best-fitting (i.e., most Guttman-pattern-like)according to their INFIT and OUTFIT mean-squares computed by Winsteps. "?"s flag the worst fitting. It can be seen that persons in the bottom half of the scalogram (from person 7 down) challenge the item hierarchy.

Person       Item
    | 8 9 6 310 1 4 5 7 2 | Fit
-------------------------------
 15 | 1 1 1 1 1 1 1 1 1 1 |
 12 | 1 1 1 1 1 1 1 1 1 0 |
 14 | 1 1 1 1 0 1 1 1 1 1 |
 17 | 1 1 1 1 1 1 1 0 1 1 |
 20 | 1 1 1 1 1 1 1 0 1 1 |
  3 | 1 1 1 1 1 1 0 1 0 1 |
  8 | 1 1 1 1 1 1 0 1 0 1 |
 23 | 1 1 1 0 1 0 1 1 1 1 | +
 24 | 1 1 1 1 1 1 1 0 0 0 |
 26 | 1 1 0 1 1 1 1 0 1 0 |
  9 | 1 1 1 0 1 0 1 0 1 0 |
 25 | 1 1 1 1 0 0 0 1 1 0 |
  1 | 1 1 1 0 1 0 0 1 0 0 |
  4 | 1 1 0 1 0 1 0 1 0 0 |
  - - - - - - - - - - - - - -
  7 | 0 0 1 1 0 1 0 1 0 1 | ?
 13 | 1 1 0 0 0 0 1 1 1 0 |
 28 | 1 0 1 1 0 1 0 0 0 1 |
 22 | 1 0 1 0 0 0 1 0 1 0 |
  2 | 1 0 0 0 1 0 0 1 0 0 |
 10 | 0 0 0 1 0 0 0 1 0 1 | ?
 11 | 0 0 1 1 0 1 0 0 0 0 |
 16 | 1 1 0 0 1 0 0 0 0 0 |
 27 | 1 1 0 0 1 0 0 0 0 0 |
 30 | 0 1 0 0 0 0 1 0 1 0 |
  5 | 0 0 1 0 0 0 0 1 0 0 |
  6 | 0 0 0 0 0 0 1 0 1 0 | ?
 18 | 0 0 0 1 0 1 0 0 0 0 |
 19 | 0 0 0 0 0 0 1 0 0 0 | ?
 29 | 0 0 0 0 1 0 0 0 0 0 |
 21 | 0 0 0 0 0 0 0 0 0 0 |
-----------------------------
Fit:| +       ?   ? ?     |
    | 8 9 6 310 1 4 5 7 2 |

Since this scalogram is so small, we can quickly determine by eye some of the structural features in it. Items 8 and 9 pair up. Perhaps this is because they are both easier items, but perhaps they contradict the criterion of local independence. Items 3 and 1 pair up for person 18 (near the bottom), and also frequently as the eye follows them up the scalogram. Similarly for items 4 and 7 from person 6 up. In contrast, items 4 and 5 tend to be in opposition.

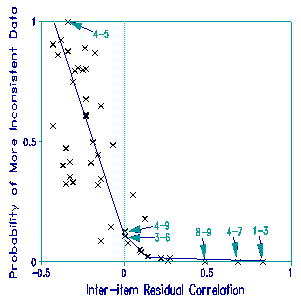
T-Rasch recommends the investigation of specific item pairs, but also implements a test of the general hypothesis that pairs of items exhibit local independence under the Rasch model. The graph presents the results. For each item pair, the x-coordinate is the correlation of the observation residuals (computed by Winsteps). The y-coordinate is the probability of observing more inconsistent data (i.e., data apparently more locally dependent) under Rasch model conditions. The trend line is drawn by eye.

The three item pairs identified by eye are the three item pairs reported as .000 by T-Rasch. These also have the highest inter-item residual correlations. .000 means that in simulating 1,000 data sets that with the same characteristics as the observed one, but under Rasch model conditions, none manifested less local independence than the observed data set for these pairs of items. Thus, these pairs of items fail this test of local independence.

Item pairs 4-9 and 3-6 exhibit empirical local independence, because their residual correlations are zero. If the data fit the Rasch model exactly, then all residual correlations would be statistically zero.

Item pair 4-5 is reported as being more consistent with the local Rasch model than 996 of 1000 simulated data sets. It is seen that the negative correlation of this pair is interpreted as indicating more local independence than even a zero correlation.

This is a thought-provoking reversal of a frequent misunderstanding in interpreting Rasch fit statistics. The usual temptation is to conceptualize misfit as occurring in only one direction, that is away from a perfect Guttman pattern. The more the departure, the worse the fit. This way of thinking overlooks that fact that some randomness is need in the data in order to construct a measurement system.

In the case of local independence, however, the fit interpretation is reversed. The closer the data comes to the perfect Guttman pattern the less local independence there is, and so the worse the fit. But this does not mean that the further from the Guttman pattern, the better, as item pair 4-5 demonstrates.

The moral of the story: Whenever a data set looks too good according to the fit criterion of the moment, the analyst needs to be especially alert to failure of the data to meet other, perhaps more crucial, criteria.

John Michael Linacre

Ponocny, I. & Ponocny-Seliger, E. (1999) T-Rasch program. Groningen, The Netherlands: ProGAMMA.

; Winsteps control and data file
title="T-Rasch Data"
prcomp=R  ; raw residuals
name1=2 ; start of person id
namelength=2 ; length of person id
item1=6 ; start of response string
ni=10 ; number of items
xwide=2 ; responses are 2 characters wide
codes=" 1 0" ; valid response codes
&end
8  ; original item number
9
6
3
10
1
4
5
7
2
END NAMES
 15 | 1 1 1 1 1 1 1 1 1 1 |
 12 | 1 1 1 1 1 1 1 1 1 0 |
 14 | 1 1 1 1 0 1 1 1 1 1 |
 17 | 1 1 1 1 1 1 1 0 1 1 |
 20 | 1 1 1 1 1 1 1 0 1 1 |
  3 | 1 1 1 1 1 1 0 1 0 1 |
  8 | 1 1 1 1 1 1 0 1 0 1 |
 23 | 1 1 1 0 1 0 1 1 1 1 | +
 24 | 1 1 1 1 1 1 1 0 0 0 |
 26 | 1 1 0 1 1 1 1 0 1 0 |
  9 | 1 1 1 0 1 0 1 0 1 0 |
 25 | 1 1 1 1 0 0 0 1 1 0 |
  1 | 1 1 1 0 1 0 0 1 0 0 |
  4 | 1 1 0 1 0 1 0 1 0 0 |
  7 | 0 0 1 1 0 1 0 1 0 1 | ?
 13 | 1 1 0 0 0 0 1 1 1 0 |
 28 | 1 0 1 1 0 1 0 0 0 1 |
 22 | 1 0 1 0 0 0 1 0 1 0 |
  2 | 1 0 0 0 1 0 0 1 0 0 |
 10 | 0 0 0 1 0 0 0 1 0 1 | ?
 11 | 0 0 1 1 0 1 0 0 0 0 |
 16 | 1 1 0 0 1 0 0 0 0 0 |
 27 | 1 1 0 0 1 0 0 0 0 0 |
 30 | 0 1 0 0 0 0 1 0 1 0 |
  5 | 0 0 1 0 0 0 0 1 0 0 |
  6 | 0 0 0 0 0 0 1 0 1 0 | ?
 18 | 0 0 0 1 0 1 0 0 0 0 |
 19 | 0 0 0 0 0 0 1 0 0 0 | ?
 29 | 0 0 0 0 1 0 0 0 0 0 |
 21 | 0 0 0 0 0 0 0 0 0 0 |

Explorations into Local Independence with T-Rasch Ponocny, I., Ponocny-Seliger,E. … Rasch Measurement Transactions, 1999, 13:3 p. 710

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt133m.htm

Website: www.rasch.org/rmt/contents.htm