The Saltus Model

A fundamental concept underlying most Rasch model applications is Thurstone's 1928 precept: "Within the range of objects for which the measure instrument is intended, its function must be independent of the object of measurement." (American J. of Sociology, 33, 529-554)

But what if this isn"t so? What if there are two or more types of person to be measured for which the measuring instrument behaves differently? For instance, a language test administered to native and non-native speakers. If the persons can be separated by type, then an immediate solution is to construct a measuring system for each type. If the persons can"t be separated, then there is a "mixture" situation. One population (or type) of persons is mixed with another.

A particular "mixture" is that addressed by the Saltus (Lat. "leap") model (Wilson, 1989). The persons are at different levels of psychological development - and the leap from one level to the next changes the way in which the measuring instrument operates. We can guess an individual's level, but not with certainty. We assume that we can identify those items which we expect to operate differently for persons at different levels.

In the simplest case, it is hypothesized that, at each level, the persons can be treated as randomly sampled from a normally distributed population, with a specific mean and standard deviation for that level. Also, while in other mixture models, each dichotomous item has a specific difficulty calibration for persons at that level, the Saltus model is simpler and estimates a much smaller number of parameters: the amount (measured in logits) that each set of items "shifts" in difficulty when encountered by persons in each level.

Thus what needs to be estimated are:
(a) The mean and standard deviation of each level's sample.
(b) The proportion of the total sample at each level.
(c) The difficulty calibration of each item at each level.

An estimation approach is to apply the MMLE (marginal maximum likelihood) formulation with an EM (expectation-maximization) algorithm. At each point, some of the parameters are estimated while others are held steady. Generally this process converges to a stable set of estimates.

From the final estimates, the probability that any particular person belongs to any particular level can be computed. These probabilities can be summed, so that, for instance, the proportion of second-grade boys at a particular level can also be estimated. For individual reporting purposes, it is conventional to consider each person to be at the level with the highest probability for that person, although some people may have a profile of probabilities that are fairly equal across levels.

Mark Wilson kindly assisted with this description.

Mislevy, R.J., & Wilson, M. (1996). Marginal maximum likelihood estimation for a psychometric model of discontinuous development. Psychometrika, 61(1), 41-71.

Wilson, M. (1989). Saltus: A psychometric model for discontinuity in cognitive development. Psychological Bulletin, 105, 276-289.

Wilson M. & Draney K. (1997) Partial credit in a developmental context: the case for adopting a mixture model approach. Chap. 18 in M. Wilson, G. Engelhard, Jr., K Draney, Objective Measurement: Theory into Practice, vol. 4. Greenwich CT: Ablex.

A computer program for estimating this model (and a polytomous version) is available from Karen Draney (kdraney at clink.berkeley.edu).

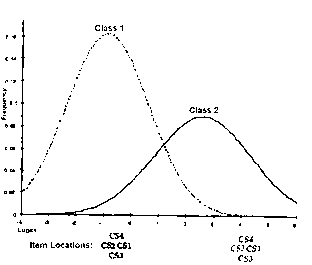
Results of a dichotomous Saltus analysis (Wilson & Draney, 1997)

Items CS1-4 are shown at their difficulty levels for Class 1 (to left) and Class 2 (to right) in the same frame of reference. In this unusual example, the items are more difficult for the higher ability class, because their increased knowledge misleads them into using an incorrect answering strategy.

The Saltus Model, Wilson M. … Rasch Measurement Transactions, 2004, 17:4 p.953

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt174c.htm

Website: www.rasch.org/rmt/contents.htm