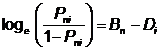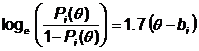Rasch Dichotomous Model vs. One-parameter Logistic Model (1PL 1-PL)

Aspect	Rasch Dichotomous Model	Item Response Theory: One-Parameter Logistic Model
Abbreviation	Rasch	1-PL IRT, also 1PL
For practical purposes	When each individual in the person sample is parameterized for item estimation, it is Rasch.	When the person sample is parameterized by a mean and standard deviation for item estimation, it is 1PL IRT.
Motivation	Prescriptive: Distribution-free person ability estimates and distribution-free item difficulty estimates on an additive latent variable	Descriptive: Computationally simpler approximation to the Normal Ogive Model of L.L. Thurstone, D.N. Lawley, F.M. Lord
Persons, objects, subjects, cases, etc.	Person n of ability Bn, or Person ν (Greek nu) of ability βn in logits	Normally-distributed person sample of ability distribution θ, conceptualized as N(0,1), in probits; persons are incidental parameters
Items, agents, prompts, probes, multiple-choice questions, etc.; items are structural parameters	Item i of difficulty Di, or Item ι (Greek iota) of difficulty δι in logits	Item i of difficulty bi (the "one parameter") in probits
Nature of binary data	1 = "success" - presence of property 0 = "failure" - absence of property	1 = "success" - presence of property 0 = "failure" - absence of property
Probability of binary data	Pni = probability that person n is observed to have the requisite property, "succeeds", when encountering item i	Pi(θ) = overall probability of "success" by person distribution θ on item i
Formulation: exponential form e = 2.71828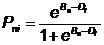
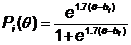Formulation: logit-linear form loge = natural logarithm
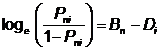
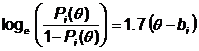
Local origin of scale: zero of parameter estimates	Average item difficulty, or difficulty of specified item. (Criterion-referenced)	Average person ability. (Norm-referenced)
Item discrimination	Item characteristic curves (ICCs) modeled to be parallel with a slope of 1 (the natural logistic ogive)	ICCs modeled to be parallel with a slope of 1.7 (approximating the slope of the cumulative normal ogive)
Missing data allowed	Yes, depending on estimation method	Yes, depending on estimation method
Fixed (anchored) parameter values for persons and items	Yes, depending on software	Items: depending on software. Persons: only for distributional form.
Fit evaluation	Fit of the data to the model Local, one parameter at a time	Fit of the model to the data Global, accept or reject the model
Data-model mismatch	Defective data do not support parameter separability in an additive framework. Consider editing the data.	Defective model does not adequately describe the data. Consider adding discrimination (2-PL), lower asymptote (guessability, 3-PL) parameters.
Differential item functioning (DIF) detection	Yes, in secondary analysis	Yes, in secondary analysis
First conspicuous appearance	Rasch, Georg. (1960) Probabilistic models for some intelligence and attainment tests. Copenhagen: Danish Institute for Educational Research.	Birnbaum, Allan. (1968). Some latent trait models. In F.M. Lord & M.R. Novick, (Eds.), Statistical theories of mental test scores. Reading, MA: Addison-Wesley.
First conspicuous advocate	Benjamin D. Wright, University of Chicago	Frederic M. Lord, Educational Testing Service
Widely-authoritative currently-active proponent	David Andrich, Univ. of Western Australia, Perth, Australia	Ronald Hambleton, University of Massachusetts
Introductory textbook	Applying The Rasch Model.T.G. Bond and C.M. Fox	Fundamentals of Item Response Theory. R.K. Hambleton, H. Swaminathan, and H.J. Rogers.
Widely used software	Winsteps, RUMM, ConQuest	Logist, BILOG
Minimum reasonable sample size	30	200 (Downing 2003)

See also: Andrich, D. (2004) Controversy and the Rasch model: A characteristic of incompatible paradigms? Medical Care, 42, 7-16. Reprinted in E.V. Smith & R.M. Smith, Introduction to Rasch Measurement: Theory, Models and Applications. JAM Press, Minnesota. Ch. 7 pp 143-166.

Downing S.M. (2003) Item response theory: applications of modern test theory for assessments in medical education. Medical Education, 37:739-745.

Linacre J.M. (2005). Rasch dichotomous model vs. One-parameter Logistic Model. Rasch Measurement Transactions, 19:3, 1032

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt193h.htm

Website: www.rasch.org/rmt/contents.htm