
The only requirement on the judging plan is that there be enough linkage between all elements of all facets that all parameters can be estimated without indeterminacy within one frame of reference. Fig. A.5 illustrates an ideal judging plan for both conventional and Rasch analysis. The 1152 ratings shown are a set of essay ratings from the Advanced Placement Program of the College Board. These are also discussed in Braun (1988). This judging plan meets the linkage requirement because every element can be compared directly and unambiguously with every other element. Thus it provides precise and accurate measures of all parameters in a shared frame of reference.
Less data intensive, but also less precise, Rasch estimates can be obtained so long as overlap is maintained. Fig. A.7 illustrates such a reduced network of observations which still connects examinees, judges and items. The parameters are linked into one frame of reference through 180 ratings which share pairs of parameters (common essays, common examinees or common judges). Accidental omissions or unintended ratings would alter the judging plan, but would not threaten the analysis. Measures are less precise than with complete data because 83% less observations are made.
Judging is time-consuming and expensive. Under extreme circumstances, judging plans can be devised so that each performance is judged only once. Even then the statistical requirement for overlap can usually be met rather easily. Fig. A.8 is a simulation of such a minimal judging plan. Each of the 32 examinees' three essays is rated by only one judge. Each of the 12 judges rates 8 essays, including 2 or 3 of each essay type. Nevertheless the examinee-judge-essay overlap of these 96 ratings enables all parameters to be estimated unambiguously in one frame of reference. The constraints used in the assignment of essays to judges were that (1) each essay be rated only once; (2) each judge rate an examinee once at most; and (3) each judge avoid rating any one type of essay too frequently. The statistical cost of this minimal data collection is low measurement precision, but this plan requires only 96 ratings, 8% of the data in fig. A.5. A practical refinement of this minimal plan would allow each judge to work at his own pace until all essays were graded, so that faster judges would rate more essays. A minimal judging plan of this type has been successfully implemented (Lunz et al., 1990).
|
Judge Essay |
1 ABC |
2 ABC |
3 ABC |
4 ABC |
5 ABC |
6 ABC |
7 ABC |
8 ABC |
9 ABC |
10 ABC |
11 ABC |
12 ABC |
|
Person1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
553 454 434 345 443 544 545 553 343 564 535 436 445 446 548 644 414 334 747 443 242 564 446 332 543 644 342 343 433 542 325 644 |
686 542 544 426 548 846 665 763 643 766 524 644 486 533 855 653 817 655 745 666 443 765 566 422 664 764 346 463 444 564 514 744 |
877 445 343 232 656 843 454 655 643 884 537 444 657 333 743 547 625 443 837 735 336 747 753 334 544 955 334 335 323 244 313 445 |
687 534 555 545 545 565 667 675 645 776 544 546 566 344 746 545 628 445 756 556 465 666 646 433 657 756 344 334 446 655 425 545 |
777 334 433 445 657 633 755 775 534 655 545 666 246 545 766 643 536 243 755 557 245 864 444 322 646 545 346 465 334 445 315 533 |
685 344 544 225 448 367 646 653 523 667 435 555 366 343 656 454 518 473 847 557 243 577 565 214 544 658 234 573 333 224 314 553 |
565 433 563 464 558 788 773 773 665 875 546 574 368 463 665 556 425 445 664 588 263 667 475 423 454 655 256 341 235 546 334 567 |
667 526 443 456 466 673 785 656 674 778 557 445 448 353 765 467 618 747 688 667 245 576 388 223 448 867 256 475 336 575 225 584 |
586 444 554 642 464 666 874 784 753 778 326 745 467 354 854 666 717 654 737 666 441 667 576 323 547 776 345 442 423 645 525 664 |
567 445 454 446 448 566 565 576 546 667 446 356 348 346 666 447 627 445 656 557 253 557 557 313 545 646 345 243 336 446 314 447 |
776 533 443 445 547 564 745 573 545 649 456 763 569 462 862 558 639 435 847 476 342 667 557 233 456 756 256 462 323 432 324 556 |
696 534 343 335 348 454 447 574 765 888 334 676 349 363 844 667 436 334 938 488 254 785 776 223 464 885 253 272 343 555 314 364 |
Figure A.5. Complete judging plan for the Essay data.
(Courtesy: Robert G. Cameron of the College Board).
|
Judge Essay |
1 ABC |
2 ABC |
3 ABC |
4 ABC |
5 ABC |
6 ABC |
7 ABC |
8 ABC |
9 ABC |
10 ABC |
11 ABC |
12 ABC |
|
Person1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
553 436 445 747 343 |
686 542 533 666 444 |
445 343 743 336 244 |
555 545 545 756 666 |
445 657 536 557 444 |
448 367 473 243 214 |
788 773 368 667 454 |
785 656 353 388 867 |
784 753 854 323 345 |
546 667 447 545 243 |
649 456 639 756 323 |
334 676 334 253 555 |
|
31 32 |
rating performed by any available judges rating performed by any available judges |
|||||||||||
Figure A.7. Rotating test book judging plan.
|
Judge Essay |
1 ABC |
2 ABC |
3 ABC |
4 ABC |
5 ABC |
6 ABC |
7 ABC |
8 ABC |
9 ABC |
10 ABC |
11 ABC |
12 ABC |
|
Person 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 |
... ... 4.. ... ... 5.. ... ... ... ... ... 4.. .4. ..6 .4. ... ... ... ... ... ... ... ... ... ... ... ... .4. ... ..2 ... ... |
... ... ... .2. ... ..6 ... .6. ... ... ... ... ... .3. ... 6.. ... ... 7.. ... ... ... ..6 ... ... ... ... ..3 ... ... ... ... |
... ... ... ... ... ... ... ... ... ... ... ... ... ... ... .4. .2. ... ... 7.. ... ..7 7.. ... ... ... .3. ... 3.. ... ... ..5 |
... 5.. ... ... ... ... ... ... ... .7. ... ..6 ..6 ... ... ... 6.. ... ..6 .5. ... ... ... ... ... ... ... ... ... ... .2. ... |
... .3. ... ... ..7 ... .5. ... .3. ..5 ... ... ... ... ... ... ..6 ... ... ... ... 8.. ... ... ... ... ... ... ... ... ... 5.. |
... ... ... ..5 ... ... ... ... ... ... ... ... ... ... ... ... ... 4.. .4. ... 2.. ... ... 2.. .4. ... ... ... ... ... ..4 .5. |
.6. ... ... ... ... ... ..3 ... 6.. ... ... ... ... 4.. ... ... ... .4. ... ... .6. ... ... ..3 ..4 ... ... ... ... ... ... ... |
..7 ... ... ... ... ... ... ..6 ..4 ... ... ... ... ... ... ... ... ... ... ... ... ... .8. ... ... ... 2.. ... .3. 5.. 2.. ... |
5.. ... ... ... ... ... ... ... ... 7.. ..6 ... 4.. ... ..4 ... ... ... ... ..6 ... .6. ... ... ... .7. ... ... ... ... ... ... |
... ..5 .5. 4.. .4. ... ... 5.. ... ... ... ... ... ... 6.. ... ... ... ... ... ..3 ... ... ... ... ..6 ... ... ... ... ... ... |
... ... ..3 ... 5.. .6. ... ... ... ... 4.. ... ... ... ... ..8 ... ... ... ... ... ... ... ... 4.. ... ..6 ... ... .3. ... ... |
... ... ... ... ... ... 4.. ... ... ... .3. .7. ... ... ... ... ... ..4 ... ... ... ... ... .2. ... 8.. ... 2.. ..3 ... ... ... |
Figure A.8. Minimal effort judging plan.

Raw scores provide a Procrustean solution to the problem of connectedness: a rating of "1" implies the same level of performance everywhere, i.e, all judges are equally severe. Rasch says that the meaning of a "1" depends on its context. This enables more meaning to be extracted from the data, but also requires more care of the analyst and test designer. In Facets, Procrustean solutions are still available through the use of anchoring.
Facets attempts to discover if the data permit the construction of one unambiguous measurement system. Specify Subset detect=No to bypass detection. Use this to speed up later runs, once data connectivity has been verified.
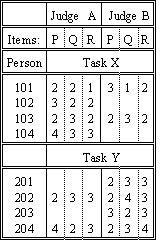
A continuing practical problem in rating performances is eliminating ambiguity introduced by deficient judging plans. Consider the data shown in the table. At first glance, all seems well. The three items, P, Q, R, can be in one frame of reference, because they share the same judge-person-task combinations. The two judges, A, B, can be in the same frame of reference, because they rate every second person together. Now comes the problem. The persons seem to share the same frame of reference because so many of them are rated on the same tasks. But there are two tasks. Why are the four 100-group people rated lower on Task X than the four 200-group people on Task Y? Are the 100-group people less able than the 200-group? Is Task X is harder than Task Y? These data cannot say which!
Resolving this ambiguity requires perception and decision. The first step is to notice the problem. If you detect it during data collection, a slight change to the judging plan can remedy the situation. For instance, some people could be asked to perform both tasks. Nevertheless, continue to be on the look out for this ambiguity during analysis.
"Complete data" such as when every judge rates every person on every item is almost always connected. Lack of connectedness is usually a result of the accidental or deliberate manner in which the data was collected, e.g., the judging plan.
Two elements are connected if there exist connections through
either i) patterns of non-extreme high ratings
and ii) patterns of non-extreme low ratings
or iii) constraints, such as anchor values.
Facets examines the data for connectedness using a much enhanced version of a joining algorithm (Weeks D.L. and Williams D.R., 1964, A note on the determination of connectedness in an N-way cross classification. Technometrics, 6/3, 319-324).
There are exotic forms of connectedness which Facets may falsely report as disconnected. Please alert MESA Press if this happens in a practical situation.
Beware! Lack of connectedness means that Facets output is ambiguous, perhaps even misleading. Only measures in the same subset are directly comparable. A separate set of vertical rulers is produced for each disjoint subset. These help you identify causes and remedies.
When a lack of connectivity is discovered, Facets reports subsets of connected elements:
---------------------------------------------------------------------------------- |Obsvd Obsvd Obsvd Fair | Calib Model | Infit Outfit | | |Score Count Average Avrge | Logit Error | MnSq Std MnSq Std | Nu student | ---------------------------------------------------------------------------------- | 16 10 1.6 1.5 | 0.09 0.64 | 0.8 0 0.8 0 | 1 1 | in subset: 1 | 11 10 1.1 1.0 | -2.25 0.85 | 0.5 0 0.4 -1 | 2 2 | in subset: 1 | 16 10 1.6 1.3 | -0.45 0.64 | 0.9 0 0.8 0 | 11 11 | in subset: 2 | 8 10 0.8 0.9 | -3.67 0.76 | 0.8 0 0.6 0 | 12 12 | in subset: 2
Students 1 and 2 are connected in subset 1. Students 11 and 12 are connected in subset 2. The relationship between subsets 1 and 2 is ambiguous. This means that all logit values in subset 1 can be increased or decreased by the same amount, relative to subset 2, without altering the fit of the data to the measurement model. Student 1 is 0.09+2.25=2.34 logits more able than student 2, but student 1's relationship to student 11 is not known, and may not be 0.09+0.45=0.54 logits more able.
Data collection may have already concluded before the first Facets analysis is made. Consequently, when Facets warns you of lack of connectedness, as in this example, there are two choices for resolving the problem. Either the tasks are "said to be alike" or the people are "said to be alike". It is wise to try both options. If Task X and Task Y were intended to have the same difficulty, then anchor them together at the same calibration, usually 0. This resolves the ambiguity, and interprets the overall score difference between the 100-group and the 200-group of persons as a difference in ability levels. On the other hand, you may have intended that the tasks be different by an amount unknown as yet, but have allocated persons to the tasks more or less at random, intending to obtain two randomly equivalent groups. Then a solution is to treat the two groups of persons as though they estimate the same mean ability. Code each person element with a 0 logit ability and a group number. Then specify group anchoring to set the mean ability level of the 100-group at the same value as the mean ability level of the 200-group. Now the overall score difference between the 100-group and the 200-group will express a difference in difficulty between Task X and Task Y.
Whenever possible, Facets should be run on available data even before data collection has concluded. Then elements identified as disconnected can be targeted for inclusion in the rating process. Thus, if it is discovered that one panel of judges has been rating the boys and another panel the girls, then some judges can be switched between panels, or some boys rated by the "girls" panel and some girls by the "boys" panel. In the example, some of these examinees, or other students like these examinees, could perform both Task X and Task Y. This would establish the relative difficulty of the tasks.
MESA Research Note #3 by John Michael Linacre,
August 1997
Go to Top of Page
Go to Institute for Objective Measurement Page
| FORUM | Rasch Measurement Forum to discuss any Rasch-related topic |
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
Our current URL is www.rasch.org
The URL of this page is www.rasch.org/rn3.htm