Are men taller than women? Are women more patient than men? We answer such questions by comparing putatively normal distributions. A typical analysis computes a t-test of differences between sample means. When samples are large, any difference between means will be declared "statistically significant". Before drawing substantive conclusions from a "significant" result, however, it is wise to discover how much the distributions overlap, contradicting any finding of clear "difference".
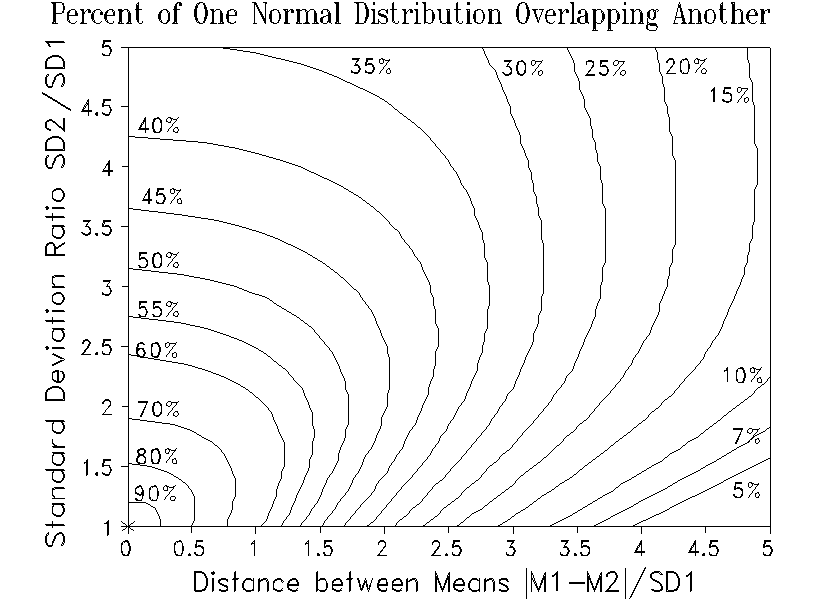
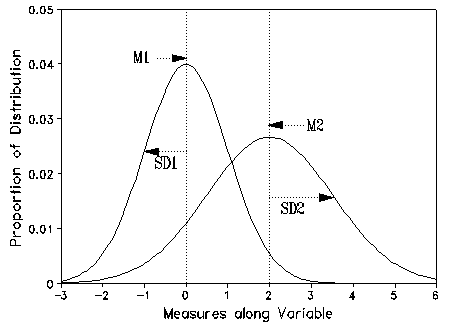
Consider two normal distributions, N1 and N2, with the same sample sizes but different means (M1 and M2) and standard deviations (SD1 and SD2). Number the samples so that N1 has the smaller standard deviation, SD1. To discover the expected percentage by which each sample distribution overlaps the other, consult the nomogram. For the x-coordinate, compute a standardized absolute distance between the means, |M2- M1|/SD1. For the y-coordinate, compute the ratio of the standard deviations, SD2/SD1. Interpolate by eye between contours to estimate the percent, p%, of each distribution that is in common with the other. The unique amount of each distribution is then 100-p%.
If M1=2.4, SD1=1.6, and M2=3.2, SD2=2.0, then |M2-M1|/SD1=0.5, SD2/SD1=1.25, and, by reference to the nomogram, about 80% of each distribution overlaps the other.
These results were computed using numerical integration of the areas under the normal curves.
Overlapping normal distributions. Linacre JM. … Rasch Measurement Transactions, 1996, 10:1 p.487
| Rasch Publications | ||||
|---|---|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch | Applying the Rasch Model 3rd. Ed., Bond & Fox | Best Test Design, Wright & Stone |
| Rating Scale Analysis, Wright & Masters | Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. | Statistical Analyses for Language Testers, Rita Green |
| Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement | Rasch models for measurement, David Andrich | Constructing Measures, Mark Wilson | Rasch Analysis in the Human Sciences, Boone, Stave, Yale |
| in Spanish: | Análisis de Rasch para todos, Agustín Tristán | Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez | ||
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Aug. 11 - Sept. 8, 2023, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Aug. 29 - 30, 2023, Tue.-Wed. | Pacific Rim Objective Measurement Society (PROMS), World Sports University, Macau, SAR, China https://thewsu.org/en/proms-2023 |
| Oct. 6 - Nov. 3, 2023, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Facets), www.statistics.com |
| June 12 - 14, 2024, Wed.-Fri. | 1st Scandinavian Applied Measurement Conference, Kristianstad University, Kristianstad, Sweden http://www.hkr.se/samc2024 |
The URL of this page is www.rasch.org/rmt/rmt101r.htm
Website: www.rasch.org/rmt/contents.htm