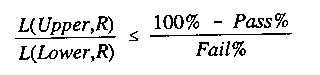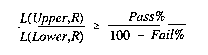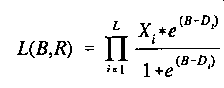Classification and Measurement

Even classification problems that require only ordinal information are assisted by good measurement practice.

A typical classification problem is: "What SAT score is a useful cut-point for College admission?" Let's disregard questions about the SAT's validity and assert that it is positively correlated with academic success. We could rank-order all College graduates and drop-outs by SAT score, and discover the one at which, in general, students at or above that score graduate and students below that score fail. Discovering the best location of that SAT score to categorize student applicants as either probable graduates or probable drop-outs is a classification problem.

The SAT example makes clear, however, that this classification problem only requires that SAT scores be ordinal indicators, not linear measures. In fact, were they only nominal, the problem might be easier. We would simply generate two lists: SAT scores with 50% or more graduation rate, and SAT scores with less than 50% graduation rate.

In practice, subjects may fall into numerous subgroups based on combinations of ordinal and nominal indicators. An example is Stineman et al.'s (1994) classification of rehabilitation patients into 53 functionally related groups based on length of stay at a rehabilitation facility and the type and severity of their impairments.

Good classification has much in common with good measurement: "An important criterion for a good classification procedure is that it not only produce accurate classifiers (within the limits of the data) but that is also provide insight and understanding into the predictive structure of the data" (Breiman et al. 1984 p.7 ­Emphasis theirs).

CAT Pass-Fail Decisions

One area where classification and measurement coincide is in making pass-fail decisions. Eggen & Straetmans (E&S, 1996) point out that a pass-fail decision on a computer-adaptive test can be thought of as a problem either in measurement or in classification.

A measurement solution could be that anyone whose measure is (a) 2 S.E.'s above the cut-point is a clear pass, (b) 2 S.E.'s below is a clear fail, (c) statistically near the cut-point is administered another item. The range from 2 S.E.'s above the cut-point to 2 S.E.'s below the cut-point forms a region of uncertainty, which reduces as more items are administered. The choice of 2 S.E.'s (or 3 S.E.'s etc.) reflects how much confidence one wants in the pass-fail decision.

E&S's classification solution is also based on measurement ideas, but implemented differently. As in the measurement solution, first choose the cut-point. Now, in advance, choose the boundaries of a hypothetical region of uncertainty, say .2 logits above the cut-point, but only .1 logit below it. We are saying that anyone whose ability lies between .2 logits above and .1 below the cut-point is too close to it for us to make a pass-fail decision. Then quantify the confidence you want in your pass-fail decision. How sure do you want to be that you pass those who should pass,and fail those who should fail? For brain-surgery, you may wish to be 90% sure to pass those who should pass, but 99% sure to fail those who should fail. For teacher recertification, you may wish to be 95% sure to pass those who should pass, but only 50% sure to fail those who should fail.

Then administer some test items using your favorite item selection algorithm so that, say, the examinee now has a score of R correct responses on L items. How do we classify this examinee as a clear pass, a clear fail or uncertain (i.e., administer more items)?

Instead of estimating the person measure, estimate the likelihood that a person whose measure is located at the upper boundary (.2 logits above the cut-point) would score R on those L items. Then compute the likelihood that a person at the lower boundary (.1 logits below the cut-point) would score R on those same L items. The classification is made from the ratio of these two likelihoods.

Mathematically, the examinee is classified a fail if:

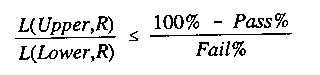
where L(Upper,R) is the likelihood of a score of R on these L items by a person whose ability is at the upper boundary, and L(Lower,R) is the likelihood for a person at the lower boundary. Pass% is the confidence level that one passes those who should pass, i.e., those whose ability is actually at or above the upper boundary. Fail% is the confidence level that one fails those who should fail, i.e.,those whose actual ability is at or below the lower boundary.

The examinee is classified a pass if

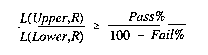
Otherwise the classification is "uncertain". If there is more than one cut-point, this same calculation can be made for the upper and lower boundaries of each cut-point. E&S perceive that, with the Rasch model, the contradictory result of passing a high cut-point, but failing a low one, can never occur.

The likelihood function is merely the product of the probabilities of each response:

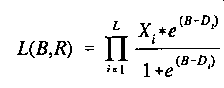
where B is the ability level corresponding to the upper or lower boundary, and X_i is 0 or 1, the scored response to item i whose difficulty is D_i. E&S report that this technique performs satisfactorily for any reasonable selection item method.

The choice between the measurement and classification solutions to CAT pass-fail decision depends on which set of pass-fail criteria is more easily established by the testing agency and simpler to explain to test consumers.

John M. Linacre

Breiman L., Friedman J.H., Olshen R.A., Stone C.J. (1984) Classification and Regression Trees. Belmont CA. Wadsworth International Group.

Eggen T.J.H.M., Straetmans G.J.J.M. (1996) Computerized Adaptive Testing for Classifying Examinees into Three Categories. Measurement and Research Department Report 96-3. Arnhem, The Netherlands: Cito.

Stineman M.G., Hamilton B.B., Granger C.V., et al. (1994) Four methods of characterizing disability in the formation of function related groups. Archives of Physical Medicine and Rehabilitation 75:12 1277-1283.

Linacre J.M. (1996) Classification and measurement. Rasch Measurement Transactions 10:2 p. 498-499.

Classification and measurement. Linacre J.M. … Rasch Measurement Transactions, 1996, 10:2 p. 498-499

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt102g.htm

Website: www.rasch.org/rmt/contents.htm