Guttman-style Item Location Maps

Maps locate, organize, identify, direct and simplify. A road map locates roads relative to important geographical features (e.g., cities), colors them according to type (major, minor, etc.), identifies them by numbers, shows us how to get from here to there, and simplifies the roads by drawing them wider than they really are,and straightening them out. All this to increase the utility of the map. A map covering the same area, but of geological formations, looks different.

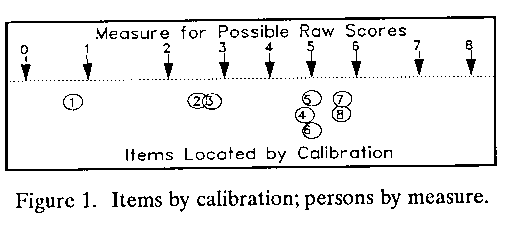
The construction of item maps follows the same logic. The purpose of a map is to communicate and inform. A map must be accurate for its intended use, but need not be bound by pedantry. A useful item map for understanding a variable locates each item exactly at its calibration and each raw score at its measure. Figure 1 is based on 8 easy Knox Cube Test items (Wright & Stone, 1979, p. 152). The items (shown below the line) are numbered in order of difficulty. Persons are measured above the line by their raw score on this test. Extreme scores (of 0 and 8) are located at the measures corresponding to expected scores that are 0.5 score points less extreme(i.e., 0.5 and 7.5).

Though this map is familiar to Rasch practitioners, it contains a paradox. A person with a raw score of 1 is to the right of item 1, i.e., above item 1. But a person with a raw score of 2 is to the left of item 2, i.e., below item 2. Yet, when asked to explain "What's the most likely way to score a `2'", we have to say, "By passing items 1 and 2".

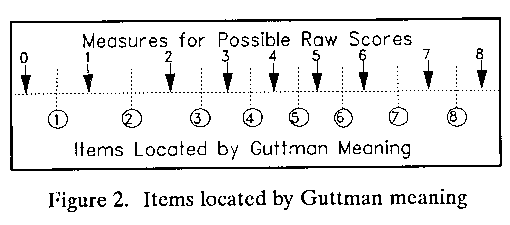
An alternative mapping technique overcomes this paradox by describing person performance informatively, at the cost of mapping items only approximately. This technique borrows from Guttman.

"If a person endorses a more extreme statement, he should endorse all less extreme statements" (Guttman 1950, p. 62).

Accordingly, we maintain the person measures, because that is the focus of this version of the map. But we relocate the items. First, we rank order the items by difficulty from easy to hard. Ties are not allowed, so items of equal difficulty are ranked according to some criterion meaningful to the intended audience (e.g., entry order on the test). Then we position each item to the left (easier-side) of the raw score corresponding to its rank, mid-way between that raw score and the one below. Thus, item 2 is relocated half-way between the measures for a score of 2 and for a score of 1 (see Figure 2).

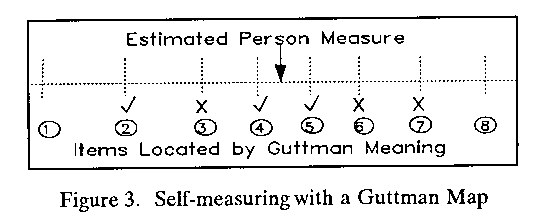
This Guttman map is particular useful for self-measuring forms, because it works even for partial test performances. Figure 3 shows a person's performance on a subset of the items. The easiest and hardest items were not administered. The estimated measure is located so that the number of failures, "X", to the left of the arrow matches the number of successes, "", to the right. This has located the person usefully in the measurement system.

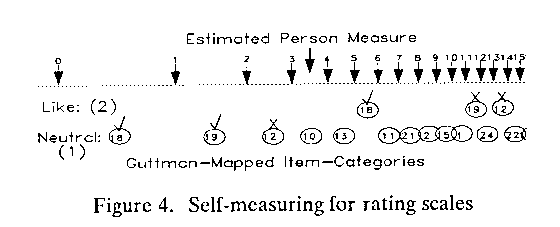
For items with rating scales, each item has as many locations as steps, i.e., ordered categories above the bottom category. The initial locations for each item (before rank ordering) are the measures for which the expected scores are the category values. The top category location corresponds to a raw score 0.25 score points less than the top category value. For a Liking for Science item (Wright & Masters,1982) the categories are 0, 1, 2. The expected scores on the upper categories are 1 and 1.75. The equivalent initial item measures for a challenging item might be 1.16 and 2.21 logits.

Once the initial locations for all categories of all items are estimated, they are rank-ordered, again ties are not allowed. Each item-category is then positioned to the left of the raw score corresponding to its rank, following the same rules as for dichotomies. Figure 4 shows part of a Guttman Map for the Liking for Science data.

Scoring and measuring are simple. Item 18 was rated "Like", so both 18 on the"Like: (2)" row and 18 on the "Neutral: (1)" row are checked. Item 19 was rated"Neutral", so on the Neutral row it is checked, but on the "Like" row it is X'd. Item 12 is rated "Dislike" (the bottom category), so it is X'd in both places. A useful measure, just by eye, for this raw score of 3 out of 6 is at a measure located between scores of "3" and "4" on the complete test.

John M. Linacre and Benjamin D. Wright

Guttman L. 1950. The basis for scalogram analysis. In S.A. Stouffer et al.Measurement and Prediction. The American Soldier Vol. IV. New York: Wiley.

Linacre J.M., Wright B.D. (1996) Guttman-style item location maps. Rasch Measurement Transactions 10:2 p. 492-493.

Guttman-style item location maps. Linacre J.M., Wright B.D. … Rasch Measurement Transactions, 1996, 10:2 p. 492-493

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt102h.htm

Website: www.rasch.org/rmt/contents.htm