Negative Information
Statistical information is a concept originated by Ronald Fisher
(1922, 1925). The information in an observation quantifies how much we
learn about the modeled variable from that observation.
There are many types of information in an observation. If we discover
from an observation that an MCQ item has an incorrect scoring key, then
we have acquired substantive information that leads us to reconsider all
statistical information acquired for that item to date. Similarly, if
we conclude from an observation that a person is applying a response set,
mechanically marking the same response option to several items, then that
behavioral information leads us to reconsider the statistical information
acquired for that person.
Suppose the data do fit the model. Then we would expect that each
extra observation would give us more statistical information, making our
conclusions more secure. For the Rasch model, this is always true. The
statistical information, Ini,in the dichotomous response
(right or wrong) of person n to item i is:
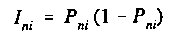
where Pni is the
probability of success. If the item is very hard then Pni is
small, and there is little statistical information (but the opportunity
for plenty of misfit if the person succeeds!). Similarly, if the item
is very easy, then (1-Pni) is small, also yielding little
information. Ini is largest when Pni=0.5, i.e.,
when the item is targeted on the person. It is with this targeting that
we have the greatest uncertainty about how the person will answer, and
so the greatest opportunity to learn more about the relationship between
the person's ability and the item's difficulty.
When an observation contains negative information, then we know
less about the variable after collecting the observation
than we did before, even when the data fit the model. Though this
paradox cannot occur with the Rasch model, it occurs in most 3PL (3-PL, three parameter logistic model)
analyses.
Imagine an ideal adaptive test. For both 3PL and Rasch, when a person
fails an item, then it is likely that the item is hard for that person,
and so an easier item is administered next.
But what if the person succeeds? Under Rasch model conditions, it is
likely the item is easy for that person, and so a harder item is
administered next. Under 3PL conditions, however, a quandary arises.
The person succeeds, but why? If success is because the item is easy for
that person, then a harder item is administered next. But if success is
due to lucky guessing, then the item is too hard for the person. (There's
no point to guessing on easy items!) This means that an easier item
should be administered next. So 3PL requires us to administer both a
harder and an easier item next leaving us more uncertain, i.e.,
less statistically informed, about the ability of the person relative to
the difficulty of the item than before the observation was made! We have
lost information, i.e., we have acquired negative statistical
information! (See Bradlow, 1996, for a mathematical formulation of this
paradox.)
Of course, the quandary can be avoided by arranging targeting and test
conditions so that respondents have little incentive to guess. This also
removes any justification for including a guessing component in the
statistical model. The few remaining lucky guesses are readily
identifiable as misfits to a guessingless-model. These can then be
dropped from the data for the purposes of calibrating the items, or
included for the purposes of measuring and diagnosing person
performance.
Benjamin D. Wright
Bradlow E.T. 1996. Teacher's corner: Negative information and the
three-parameter logistic model. Journal of Educational
Statistics 21:2 179-185.
Fisher R.A. 1922. On the mathematical foundations of theoretical
statistics.Proceedings of the Royal Society 222: 309-368.
Fisher R.A. 1925. Theory of statistical estimation. Proceedings
of the Cambridge Philosophical Society, 22: 700-725. Also in
Collected Papers of R.A. Fisher, ed.J.H. Bennett. Adelaide: The
University of Adelaide.
Wright B.D. (1996) Negative information. Rasch Measurement
Transactions 10:2 p. 504.
Negative information. Wright B.D. … Rasch Measurement Transactions, 1996, 10:2 p. 504