A Standard Setting Exercise

Longford (1996) poses an interesting problem in standard setting. 17 writing performances were randomly selected from all scored performances. They had ratings in the range 4-12. These 17 writers were each assessed as pass or fail by each of 16 experts. Now, what is the minimum rating for a pass?

-------------------------------------------------------------------
|         Expert's Classification of Writers: 1=Pass, 0=Fail      |
|-----------------------------------------------------------------|
|Writer: | 6 10 14  1  4  5  9 11 13 15 12  8 16  7 17  2  3|     |
|--------+--------------------------------------------------+-----|
|Rating: |10 12  9  8 11  8  7 11  6  8 10  9  6  6  7  4  5|Total|
|--------+--------------------------------------------------+-----|
|Expert 6| 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  0|  16 |
|    2   | 1  1  1  1  1  1  1  1  1  1  1  0  1  1  1  1  0|  15 |
|   11   | 1  1  1  1  1  1  1  1  1  1  1  1  1  1  0  1  0|  15 |
|   12   | 1  1  1  1  1  1  1  1  1  1  1  1  1  1  1  0  0|  15 |
|    5   | 1  1  1  1  1  1  1  1  1  1  1  1  1  0  0  0  0|  13 |
|    7   | 1  1  1  1  1  1  1  1  1  1  1  1  1  0  0  0  0|  13 |
|    9   | 1  1  1  1  1  1  1  1  1  1  1  1  1  0  0  0  0|  13 |
|   14   | 1  1  1  0  1  1  1  1  1  0  1  1  1  1  1  0  0|  13 |
|   16   | 1  1  1  1  0  1  1  1  0  1  1  1  1  1  1  0  0|  13 |
|    1   | 1  1  1  1  0  1  1  1  1  1  0  1  1  1  0  0  0|  12 |
|    4   | 1  1  1  1  1  1  1  1  0  1  0  0  0  1  1  0  0|  11 |
|   15   | 1  1  1  1  1  0  1  0  1  1  0  1  0  1  1  0  0|  11 |
|    3   | 1  1  0  1  1  1  1  1  1  0  1  0  0  0  0  0  0|   9 |
|    8   | 1  1  1  0  0  1  0  1  1  0  1  0  1  0  1  0  0|   9 |
|   10   | 1  1  1  1  1  0  0  0  1  1  1  1  0  0  0  0  0|   9 |
|   13   | 1  0  1  1  1  0  0  0  0  1  0  0  0  0  0  0  1|   6 |
|--------+--------------------------------------------------+-----|
|Total   |16 15 15 14 13 13 13 13 13 13 12 11 11  9  8  3  1|  193|
-------------------------------------------------------------------

A routine Rasch analysis of Longford's data (shown Guttman-sorted in the Table) reveals that some data editing is needed. Expert 13 is the most severe and yet was the only expert to pass Writer 3 (the `1' in the bottom right corner of the data matrix). This causes Expert 13 to have large misfit statistics and a negative correlation with the other experts. He is not part of any consensus. The pass verdicts for Writer 17 also correlate negatively with the judges' perspectives of the other writers. This idiosyncratic Writer is also not part of any consensus. Once these irregular rating patterns are removed, consensus appears. Writer 3 is failed by everyone. Writers 6 and 10 are passed by everyone. In a second Rasch analysis, the writers are measured, establishing a frame of reference within which to identify the pass-fail criterion. In a third analysis, all writers are anchored at their measures from the second analysis (including Bayesian estimates for writers with extreme scores). Then measures are obtained for all experts, so that all (except 13) participate in setting the mean pass-fail point.

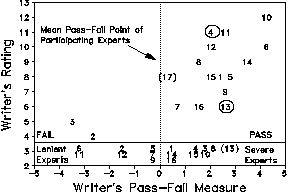Writer's ratings vs. pass-fail measures are plotted in the Figure. The experts' severity measures are across the bottom of the plot. An expert of average severity would be expected to pass all performances to the right of the Y-axis. Also shown, for reference only, are Expert (13) and Examinee (17). We see that the bulk of the experts would be expected to pass papers rated 6 or more.

This plot also warns that the original ratings themselves are dubious. Writer 13, with a rating of 6, was deemed a more certain pass by these experts than Writer 4 with a rating of 11. The standard setting process could also be improved. Rather than selecting papers at random, focus on ratings near the expected pass-fail point using a stratified random sample. A better sampling plan would eliminate most of the papers rated 9-12, and select papers rated 4-7.

John Michael Linacre

Longford NT (1996) Reconciling experts' differences in setting cut scores for pass-fail decisions. Journal of Educational Statistics 21:3 203-213.

A standard setting exercise. Linacre J.M. … Rasch Measurement Transactions, 1996, 10:3 p. 521.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt103k.htm

Website: www.rasch.org/rmt/contents.htm