Investigating Judge Local Independence

Local independence is required of data that are to support Rasch measures. Local independence exists when the Rasch measures explain all systematic differences among the data, so that there is independence among the residual differences between the observed data and those expected from the Rasch measures. When judges award ratings, it may not be obvious whether their task is to act as independent experts or merely to code data. An investigation into local independence can help to clarify this.

"Analysis of the fit of data to [local independence] is the statistical device by which data are evaluated for their measurement potential - for their measurement validity" [Wright 1991 RMT 5:3 p.159]. Yet typical chi-square fit statistics, such as INFIT and OUTFIT, detect lack of local independence only indirectly. If the same item is repeated twice in an MCQ test, then each item predicts the responses to the other too well. This means that the residuals for both items are smaller than expected, leading to smaller than expected chi-square statistics. But no direct indication is given that the two small chi-squares are caused by an interaction between these two particular items. An investigation of response covariance would immediately flag the interdependency of the two items.

Can covariance investigation also detect a lack of judge independence? A carefully conducted study of judge behavior was Rasch analyzed. Examinees performed several writing tasks. Each examinee-task performance was rated separately by each judge.

Initial analysis indicated that the spread of judge severities was about one-third that of examinee abilities. Certainly too big to be ignored. The judge mean-square chi-square fit statistics for these well-trained judges ranged from 0.5 to 1.4 - not unusual for this type of rating situation. Even though these judges seemed to be exercising their expertise independently enough, judge rating covariances were investigated.

The actual judge rating covariances were calculated from the observed ratings. Then a simulation of independent ratings was generated from the Rasch estimates of judge severity, examinee ability, writing task difficulty, and rating scale structure. The judge covariances for the simulated data were also estimated. Comparison of the covariances is intriguing.

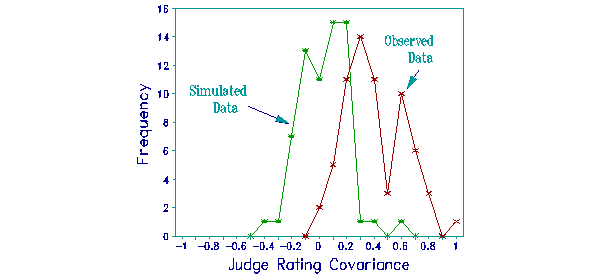
The judge plot shows the frequency of judge covariance size for the observed and simulated data sets. The covariances for the simulated, locally independent data are centered on 0, and rarely get above 0.5 score points. But none of the observed covariances are below 0, and one is just above 1 score point. The largest covariance is between two judges identified as most unpredictable (noisy) by the chi-square statistics. The covariances of the other judges with the most predictable judge are generally about 0.25 score points.

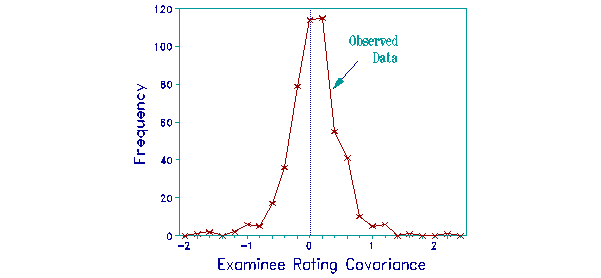
As a check on the study, the covariance of examinee responses was also computed. These are shown in the examinee plot. They raise no special concerns because their center is close to 0, with most covariances less than 0.5 score-points.

Positive judge covariances imply that when one judge gives a higher than expected rating to a particular examinee on a particular task, then the others also tend to, or when one gives a lower than expected rating, then so do the others. These tendencies are apart from any systematic rating patterns across examinees or tasks, which would raise or lower the corresponding measures. It seems there is something in particular examinee-task performances that prompts the judges, en masse, to raise or lower their severity levels. Perhaps this indicates that the judges are not exhibiting the local independence the model specifies, or perhaps it indicates local strength or weakness by subsets of examinees on tasks.

What are the measurement implications of judge over-conformity? Lack of local independence, just like other forms of misfit, degrades the measurement process and increases standard errors. The judges are acting like bathroom scales with the 0 calibrated at different weights. There must still be an adjustment for their relative severities. On the other hand, their ratings are not fully independent, so that each extra rating does not contain as much new statistical information as previous ones. This means that the precision of measurement is not as great as the number of ratings suggests. Consequently, model-based standard errors are too small.

John Michael Linacre

Investigating Judge Local Independence. Linacre J. M. … Rasch Measurement Transactions, 1997, 11:1 p. 546-7.

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt111h.htm

Website: www.rasch.org/rmt/contents.htm