Linking Tests with the Rasch Model

Equal-interval scaling provides the theoretical basis for linking tests, but linking tests is not a mechanical process. Careful thought is required. We need to consider five "C"s when undertaking the process of linking: Clean, Close,Consistent, Control and Constant.

Clean data is necessary. Item analysis quickly identifies improper scoring of items as well as those with unsatisfactory distractors. Rescore or drop such items. Off-target items provoke off-dimension responses: guessing, carelessness, response sets. Remove off-target responses. For typical multiple-choice tests, begin by discarding all test records with raw scores less than 1/3 of the maximum possible raw score. This is a conservative practice especially when the same test is given to a whole grade.

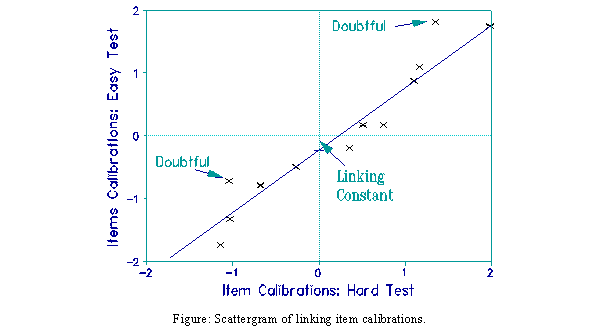
Close-together tests have the most consistent links. Close tests have item difficulty ranges of two logits or less and a mean item difficulty difference of about 3/10 of a logit. Greater separation between linked tests results in more items showing noticeable difficulty changes when plotted on a linking scattergram (see Figure). Linking tests that are too far apart is a common error. It has been shown experimentally that one logit difference in mean difficulty between two tests is too far apart for stable calibration of the two tests onto one scale.

Consistent adherence by the items to the variable measured is necessary. Tests items must lie along the same variable. Linking two tests that measure slightly different variables is a problem the severity of which increases with the difference in variables. Examine the item hierarchy. Does each item harmonize reasonably well into a common construct? Weed out discordant items that are inconsistent with the intended variable. It takes at least 40 items to get a reasonable confluence of item effects for measuring a variable.

Control over the linking items is necessary because the purpose of linking is to adjust all items in a test, not just those in the link. We need the linking items to be representative of the other items in each of the two tests that are being linked. We do not always have control over selection of the linking set of items, but when this is possible use items close to the center of difficulty for two tests rather than items of extreme difficulty. The practice of using a set of linking items that are the hardest items of one test and the easiest items on the other test is counter-productive, because off-target items are also the most unstable.

An item can be calibrated acceptably in each of two tests and yet act differently in those tests. Item interaction or specific learning of one group could be the cause. Drop these items from the linking set, and code them as different items in each test.

The linking constant must be sturdy. Rasch practitioners have often followed the rather crude practice of defining a set of items a priori, then averaging the calibrations of that set as they appeared in the two different tests, in order to establish a calibration difference that becomes the linking value to equate the two tests. This is too chancy. A link can almost always be "cleaned up" by excluding one or more of the items from the set of linking items, and this is often necessary to make the link defensible.

Replicating the linking value is helpful in deciding which linking items to omit. A third "linking" test, containing different linking items, is linked independently with each of the two tests originally linked. Hopefully this third testis close to the two original tests in difficulty. The algebraic sum of the links between the third test and the two original tests is compared with the direct link. This should confirm the accuracy of the direct link.

George Ingebo

Linking Tests with the Rasch Model. Ingebo G. … Rasch Measurement Transactions, 1997, 11:1 p. 549.

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt111k.htm

Website: www.rasch.org/rmt/contents.htm