PROX for Guessing and Carelessness

Test items don't guess and test items aren't careless. The greatest clarity comes from the detection of guessing and carelessness as misfit on the person level. Nevertheless, it is sometimes useful to work with an assertion that some items induce guessing and some items induce carelessness. Minimum competency testing procedures often encourage low performers to guess on items that are impossibly difficult for them. Some of the National Adult Literacy Survey test items are so easy that they provoke carelessness among the highly literate.

The dichotomous Rasch model can be extended to accommodate guessability and carelessness as item characteristics:

where u_i is the upper, asymptotic "carelessness" coefficient for item i, and c_i is its lower, asymptotic "guessability" coefficient, P_ni, B_n and D_i have their usual meanings.

For this model to be estimable, u_i and c_i must be specified ahead of time. They cannot be estimated simultaneously with person ability B_n and item difficulty D_i. Reasonable values for u_i and c_i can often be deduced by inspection of the items themselves or from response summary statistics for very high and very low scoring groups of test-takers.

Having made the large assertion that carelessness and guessing can be induced by items, let us further assert that the item difficulty distribution and person ability distribution can be usefully summarized by their means and standard deviations. Then PROX (normal approximation algorithm) estimates (Cohen, 1979) of ability and difficulty will be satisfactory.

Rewriting (1)

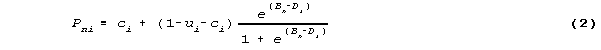
Asserting that person abilities are normally distributed, and following the argument in RMT 8:3, p. 378,

where S_i are the number of successes by the N_i persons who encountered item i. µ_i is the mean ability and _i the standard deviation of those N_i persons. is the logistic ogive. 2.9 is the standard divisor. 2.65 is a better value (RMT 11:2 p. 569).

Rearranging, produces an estimation equation for D_i, the logit difficulty of item i,

with model standard error,

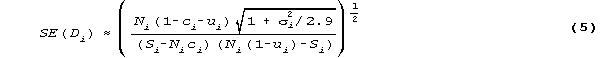
For B_n, the ability of person n, consider the items in groups, such that c_i=c_g and u_i=u_g are set constant across items within group g. Then B_ng is the ability estimate for person n based on group g of items:

where R_ng is the raw score achieved by person n on N_ng items, and µ_ng and _ng summarize the distribution of those N_ng item difficulties.

B_ng has a model standard error,

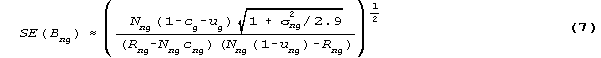
The {B_ng} can be combined to produce an estimate for B_n (RMT 8:3 p. 376):

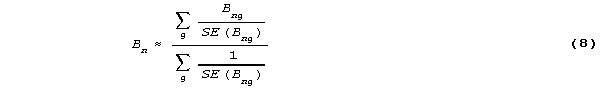
with standard error,

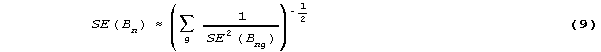
These equations can be solved iteratively, with one constraint such as D_i0, to produce estimates for the measures of all elements.

When data are complete, or responses are missing at random, and u_i=u, c_i=c are set constant across items, then µ_i and _i can also be treated as constant across items. Similarly, µ_n and _n can be treated as constant across persons. Then non-iterative solutions are:

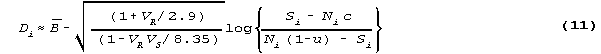
where is the mean person ability, the mean item difficulty is zero and 8.35 is the standard value. 7.0 is a better value (RMT 11:2 p. 569). Also,

To perform this by hand, see Wright & Stone (1979), Chapter 2.

John M. Linacre

Cohen, L. 1979. Approximate expressions for parameter estimates in the Rasch model. British Journal of Mathematical and Statistical Psychology 32(1) 113-120.

Wright B.D., Stone M.H. (1979) Best Test Design. Chicago: MESA Press.

PROX for Guessing and Carelessness. Linacre J. M. … Rasch Measurement Transactions, 1997, 11:2 p. 570-571.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt112n.htm

Website: www.rasch.org/rmt/contents.htm