Insights through Graphing

Conventional item analysis presents its results as tables of numbers. The Rasch model provides a framework in which familiar results can be made more meaningful and new insights can emerge. Graphical presentation is the key.

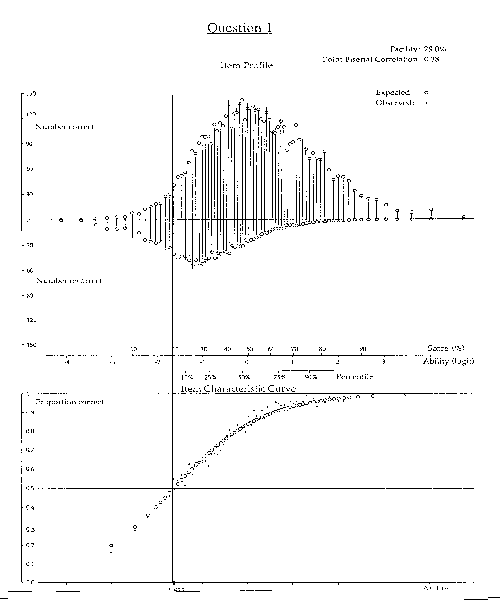
The Figure overleaf summarizes the performance of 7,132 students on Question 1 of the 1990 Australian Higher School Certificate Physics Examination. Overall, 79% of the sample succeeded on it.

The ability distributions of the students who succeeded and failed on this item are shown in the top panel of the Figure. The x-axis shows the variable in terms of percent correct on the whole test (clearly squeezed together around 50%), and also logit abilities relative to the mean sample performance. The y-axis indicates the number of students.

A secondary x-axis, immediately below the ability measures, locates percentiles for this sample. The students meriting special attention are at the tails.

The item calibration (which targets students with 50% probability of success) is shown by the vertical rule. We can confirm this by eye, because it corresponds to the location on the variable where the succeed and fail bars are of equal length.

Based on performance on the test as a whole, we would expect each vertical bar to end at a . Only a few bars are much shorter or longer, indicating generally good fit of the item for this sample.

Another perspective on Question 1 is given by the comparison of its item characteristic curves in the bottom panel. The model curve, , follows the logistic ogive for this right/wrong item. The empirical ICC is shown by . It is somewhat fuzzy, but close to the model line. High performers have done a little better than expected on this item. The few low performers somewhat worse. There is no evidence of a lower "guessing" asymptote. Most intriguing is the slight sag in performance among those about 1 logit above the item (around 70% correct). Perhaps these students have a usually successful, but slightly faulty approach: "A little knowledge is a dangerous thing!"

Andrew Stephanou
Centre for the Study of Higher Education (CSHE)
The University of Melbourne, Australia

Insights through Graphing.Stephanou A. … Rasch Measurement Transactions, 1997, 11:2 p. 571-572.

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt112p.htm

Website: www.rasch.org/rmt/contents.htm