Pivot-Anchoring Items for Construct Definition

The placement of items along a variable defines the construct. For dichotomies, the location of items by their measures is unambiguous. Construct development proceeds immediately, see Chapter 5 of Best Test Design (Wright & Stone, 1979). For rating scales, item location is more nebulous. Chapter 7 of Rating Scale Analysis (Wright & Masters, 1982) points out how the construct is redefined when different standpoints on item difficulty are adopted. When an instrument contains multiple item types, the challenge is to build a clear, comprehensive, useful and defensible construct definition.

When data are collected on a rating scale, each category threshold, "step", has its own difficulty. This can be parameterized as D_ij, the calibration of the jth step from category j-1 to category j for item i relative to the local origin of the measurement system. It can also be parameterized as D_i + F_ij, where D_i is the calibration of the item relative to the local origin and F_ij is the calibration of step j relative to D_i. Mathematically, the two forms are equivalent. Conceptually they are different.

Consider the SF-36 Health Survey instrument. It contains not only dichotomies but also rating scales with 3, 5 and 6 categories. In discussing an item on a 6 category rating scale ("All of the time" to "None of the Time"), such as "Did you feel tired", we would overwhelm ourselves, as well as our audience, were we to describe all 5 of its step calibrations. Rather, we want to locate that item at one point along the variable, so that it can be compared with a "Yes/No" dichotomy, such as "Accomplished less than you would like".

The mathematically convenient item location is the one at which F_ij=0 for the item. This is the point along the variable at which the highest and lowest categories for item i are equally probable, a type of mathematical "middle". The substantive meaning of this mathematical location, however, is usually obscure because it is an accident of how the categories have been labelled.

A more meaningful item location could be obtained by collapsing the rating scale into a dichotomy. The dichotomization of each item would be guided by one master criterion, such as "healthy vs. sick", with the actual pivot point for each item being decided by clinical judgement. Since the rating scale will not actually be collapsed into two categories, the pivot point may be in the middle of an ambivalent category, e.g., "Don't Know". Such uncertain categories, however, often contribute more noise than information and so are better treated as missing data.

Once the pivot point for each rating scale has been chosen by inspection of the category labels, then matching step calibrations can be imposed on the analysis. For instance, for the three category scale, "1. Yes, Limited A Lot", "2. Yes, Limited A Little", "3. No, Not Limited At All", the essential dichotomy between sickness and health contrasts categories 1 and 2 against category 3. The pivot point is between categories 2 and 3, where the step calibration is F_i3. This is the location relative to which the item difficulty is to be defined. Mathematically, D_i + F_i3 D_i, so, to obtain this pivot, set (anchor) F_i3=0.

The effects of anchoring steps are:

1) the data do not change unless explicitly recoded,

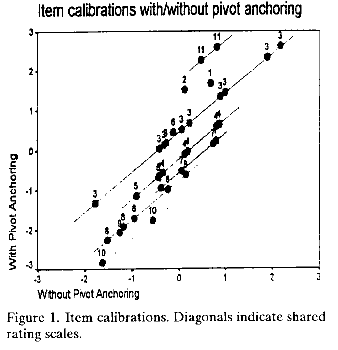
2) item difficulties do change (see Figure 1), redefining the construct. At bottom of Figure 1, the new "easiest item" is "13", previously it was the "3" at extreme left.

3) but items on the same rating scale retain their relative difficulties, so that these subsets retain their sub-construct definitions (diagonals in Figure 1),

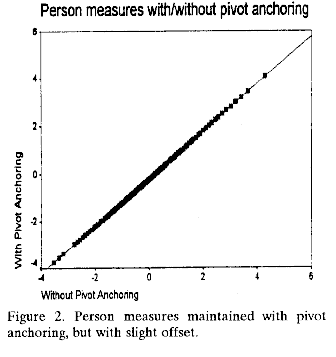
4) persons performances do not change nor do their relative measures (see Figure 2),

5) since the local origin of the measurement system is the mean item difficulty, all person measures may be changed, but by the same offsetting amount (diagonal offset in Figure 2).

Now each item difficulty is located according to a substantive criterion. Consequently, their ordering and relative location also have substantive meaning, aiding us in perceiving the criterion definition of the underlying construct.

Rita Bode
Rehabilitation Institute of Chicago

Pivot-Anchoring Items for Construct Definition. Bode R. … Rasch Measurement Transactions, 1997, 11:3 p. 576-7

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt113e.htm

Website: www.rasch.org/rmt/contents.htm