L_z - An All-Purpose Person Fit Statistic?

Li & Olejnik (1997) investigate six person fit statistics and conclude that "Practitioners need no longer be confused by the large number of possible person-fit indexes available to detect nonfitting examinees. The l_z index will provide as reliable and accurate identification of unusual responding as other person fit statistics" (p. 229). Oh joy! Oh rapture! Our fit detection problems are finally over! - But wait, Klauer (1995) cautions "a given person [index] implies a bias for detecting the [index]-specific deviations and a bias against detecting other kinds of deviations" (p. 109). Since Li & Olejnik consider only dichotomous tests, let us contain our joy while we evaluate the utility of l_z for polytomies.

l_z (Hulin et al., 1983) is a likelihood-based statistic, computed in several steps:

Step 1. Compute the likelihood, _n, of the observed response string for person n of estimated ability B_n,

where P_nix is the Rasch-model probability that person n on item i would respond in the observed category x of a 0,M rating scale. This has log-likelihood,

Step 2. Compute the expected log-likelihood,

Step 3. Compute the log-likelihood variance,

Step 4. Compute the l_z index,

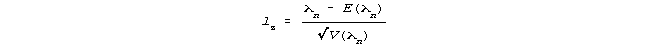
The l_z index is standardized, so that a value of 0.0 is intended to reflect a perfectly typical response string. Values greater than 2.0 could indicate unexpectedly good fit (overfit). Values below -2.0 could indicate unexpectedly poor fit (noise).

Applying this to Smith's (1996, RMT 10:3 p.516-7) simulated polytomous data produces the results in the Table. In Section A, l_z is skewed. Response strings simulated to fit the model have values around .75, rather than the proclaimed 0.0.

In Section B, overfitting (Guttman-like) response strings reach only as far as 1.9, and so are not large enough to be flagged. Response patterns corresponding to misuse of the ratings scale (central tendency, extremism, erratic behavior), often detected by INFIT and OUTFIT, are not detected by l_z.

In Section C, large negative values of l_z do usefully pin-point grossly aberrant response patterns. Even so, there was only one instance in which l_z flagged misbehavior which INFIT and OUTFIT missed. This was for the "one category" response set (Block V, line 1) which the l_z value of -2.06 flags as unexpected. However, the RPM (point-measure correlation, similar to point-biserial) value of 0.0 provides a powerful and immediate diagnosis of this response string. In general, l_z does not flag borderline response strings.

Alas, l_z is markedly less useful than INFIT and OUTFIT mean-squares. Our joy must be deferred.

John M. Linacre

Later note: Adjustment to l_z is suggested in "Assessment of Person Fit for Mixed-Format Tests", Sandip Sinharay, Journal Of Educational And Behavioral Statistics July 13, 2015

Snijders, T. (2001). Asymptotic null distribution of person-fit statistics with estimated person parameter. Psychometrika, 66, 331-342 (for dichotomous items)

Sinharay, S. (2016). Asymptotically correct standardization of person-fit statistics beyond dichotomous items. Psychometrika, 81, 992-1013 (for polytomous items)

Hulin, C.L., Drasgow F., Parsons C. (1983) Item Response Theory: Applications to Psychological Measurement. Homewood Il: Dow & Jones Irwin.

Klauer K.C. (1995) The assessment of person fit. p. 97-110. In G.H. Fischer & I.W. Molenaar (Eds.) Rasch Models: Foundations, Recent Developments and Applications. New York: Springer Verlag.

Li M.F, Olejnik S. (1997) The power of Rasch person-fit statistics in detecting unusual response patterns. Applied Psychological Measurement 21:3, p. 215-231

"It is recommended that with real tests, identification of significantly nonfitting examinees be based on empirical distributions of l_z generated from Monte Carlo simulations using item parameters estimated from real data."
l_z Person-Fit Index to Identify Misfit Students With Achievement Test Data. Dong Gi Seo and David J. Weiss. Educational and Psychological Measurement 2013;73 994-1016. epm.sagepub.com

This is the BIGSTEPS control file for the data above:

&inst
TITLE='COMPUTING STATISTICS'
NI=20
ITEM1=1           ; include response strings in person name
name1=1
namlen=30
CODES=0123
ptbis=no          ; compute point-measure correlation
INUMB=YES         ; no item labels
TFILE=*
6        ; Table 6 - persons in fit order
18       ; table 18 - persons in entry order
*
IAFILE=*          ; item anchor values - uniform
1 -1.9
2 -1.7
3 -1.5
4 -1.3
5 -1.1
6 -0.9
7 -0.7
8 -0.5
9 -0.3
10 -0.1
11 0.1
12 0.3
13 0.5
14 0.7
15 0.9
16 1.1
17 1.3
18 1.5
19 1.7
20 1.9
*
SAFILE=*          ; step anchor values
0 0
1 -1
2 0
3 1
*
&end
33333132210000001011 modelled
31332332321220000000 modelled
33333331122300000000 modelled
33333331110010200001 modelled
33222222221111111100 most expected
33333222221111100000 most likely
33333333221100000000 high discrimination
32222222221111111110 low discrimination
32323232121212101010 tight progression
33333333332222222222 high (low) categories
22222222221111111111 2 central categories
33333322222222211111 only 3 categories
32222222201111111130 noisy outliers
33233332212333000000 erratic transitions
33333333330000000000 extreme categories
33133330232300101000 noisy progression
22222222222222222222 one category
12121212121212121212 central flip-flop
03202002101113311002 random responses
01230123012301230123 rotate categories
03030303030303030303 extreme flip-flop
11111122233222111111 folded pattern
22222222223333333333 high reversal
11111111112222222222 central reversal
00111111112222222233 Guttman reversal
00000000003333333333 extreme reversal

An All-Purpose Person Fit Statistic? Linacre J.M. … Rasch Measurement Transactions, 1997, 11:3 p. 582-3.

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt113n.htm

Website: www.rasch.org/rmt/contents.htm