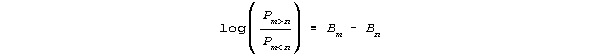
A paradox of statistics is that more elaborate, highly parameterized models often neither describe the data better nor provide as robust a basis for inference as simpler measurement models. A case in point is M. H. Birnbaum's (1991) finding that three types of judgements must be combined to successfully scale the items on the Schedule of Recent Events (Holmes & Rahe, 1967). In his study, 95 subjects contrasted 15 stressful events, by being asked to judge:
(1) the relative stress of pairs of events as ratios, e.g., 1/8, 1/4, ½, 1, 2, 4, 8;
(2) the relative stress of pairs of events as differences, using a 200-point rating scale where 0 = No difference between the pair, 100 = event 1 very much more stressful than event 2, and -100 = event 2 is very much more stressful than event 1;
(3) the stress produced by all possible combinations of one, two, and three events, where 0 = No stress at all and 100 = maximal stress.
These resulted in 309 judgements per subject, which were then consolidated to produce a "unified" scale of stressful events.
Is such a complex data-intensive procedure necessary to produce a useful scale for these stressful events? The Rasch model for dichotomous paired-comparisons:
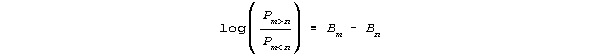
is not only much more simple, but encompasses both ratio and difference scaling. Like every Rasch model, it requires the data to fit the model according to probabilistic specifications. As a result, problems caused by data imprecision and sample dependence are exposed and addressed.
Using new judgements of the 15 stressful events, in which 13 persons each made only 14 paired-comparison judgements, a Rasch-calibrated scale was constructed. The Figure plots it against Birnbaum's scale. The two methods produce the same scale of stressful events, but each Rasch subject made 95% fewer judgements. The Rasch data also distinguish between "Divorce" and "Jail Term" and so are more plausible than Birnbaum's data which scales them the same.
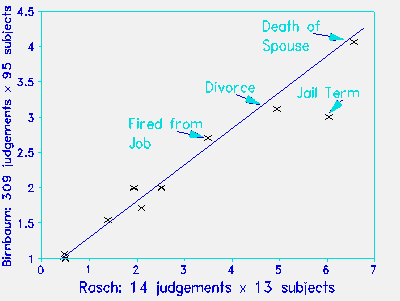
William of Occam asserted that "What can be accounted for by fewer assumptions is explained in vain by more." When choosing between equally fruitful approaches, the simpler one is to be preferred. Complex item response models are often mistaken to be more effective than simpler, more profound models. This illustration refutes that misguided notion.
Karabatsos G. (1998) Occam's Razor At Work. Rasch Measurement Transactions 11:4 p. 587-8.
Birnbaum M.H., Sotoodeh Y. (1991) Measurement of stress: Scaling the magnitudes of life changes. Psychological Science 2(4) 236-243.
Holmes T.H., Rahe R.H. (1967) The social readjustment scale. Journal of Psychosomatic Research 11 213-218.
Occam's Razor At Work. Karabatsos G. … Rasch Measurement Transactions, 1998, 11:4 p. 587-8.
| Rasch Publications | ||
|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch |
| Applying the Rasch Model 2nd. Ed., Bond & Fox | Best Test Design, Wright & Stone | Rating Scale Analysis, Wright & Masters |
| Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. |
| Statistical Analyses for Language Testers, Rita Green | Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement |
|
|
|
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| June 19-21, 2013, Wed.-Fri. | SIS 2013 Conference on Advances in Latent Variables: Methods, Models and Applications, Brescia, Italy, meetings.sis-statistica.org/index.php/sis2013/ALV |
| July 1 - Nov. 30, 2013, Mon.-Sun. | Online Course: Introduction to Rasch Measurement Theory (D. Andrich, RUMM), www.education.uwa.edu.au/ppl/courses |
| July 5 - Aug. 2, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| July 15, 2013, Monday | Application deadline: UIC Educational Research Methodology online graduate certificate program, www.go.uic.edu/OnlineMESA |
| July 22, 2013, Monday | Submission deadline: 2014 AERA Annual Meeting, Philadelphia PA, www.aera.net |
| Aug.1-5, 2013, Thur.-Mon. | TERA-PROMS Annual Meeting, Kaohsiung, Taiwan, tera.education.nsysu.edu.tw |
| Aug. 9 - Sept. 6, 2013, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Aug. 22, 2013, Thursday. | Symposium in honor of Svend Kreiner, Copenhagen, Denmark, biostat.ku.dk/kreinersymposium |
| Sept. 4-6, 2013, Wed.-Fri. | IMEKO TC1-TC7-TC13 Symposium: Measurement Across Physical and Behavioural Sciences, Genoa, Italy, www.imeko-genoa-2013.it |
| Sept. 13 - Oct. 11, 2013, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 18-20, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 23-25, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 26-27, 2013, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Oct. 18 - Nov. 15, 2013, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Oct. 20 - Oct. 25, 2013, Sun.-Fri. | International Association for Educational Assessment (IAEA) 39th Annual Conference, Tel Aviv, Israel, www.iaea-2013.com |
| Dec. 11-13, 2013, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| March 12-14, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| April 3-7, 2014, Thurs.-Mon. | AERA Annual Meeting, Philadelphia PA, www.aera.net |
| May 14-16, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| May 19-21, 2013, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| July 4 - Aug. 1, 2014, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 8 - Sept. 5, 2014, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
| Sept. 10-12, 2014, Wed.-Fri. | In-person workshop: Introductory Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 12 - Oct. 10, 2014, Fri.-Fri. | On-line workshop: Rasch Applications in Clinical Assessment, Survey Research, and Educational Measurement (W.P. Fisher), www.statistics.com |
| Sept. 15-17, 2014, Mon.-Wed. | In-person workshop: Intermediate Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| Sept. 18-19, 2014, Thurs.-Fri. | In-person workshop: Advanced Rasch (A. Tennant, RUMM), Leeds, UK, www.leeds.ac.uk/medicine/rehabmed/psychometric |
| The javascript to add "Coming Rasch-related Events" to your webpage is: <script type="text/javascript" src="http://www.rasch.org/events.txt"></script> | |
The URL of this page is www.rasch.org/rmt/rmt114b.htm
Website: www.rasch.org/rmt/contents.htm