Do Correlations Prove Scores Linear?

Alan Tennant writes:
"My concern is that papers are being published which (1) use correlations between raw scores and Rasch measures to argue that raw scores are interval if the correlation between the two is high, and (2) link the center of the ogive to interval-level measurement."

"What must I do to break this link between the near equal-spaced progression of central raw scores and the argument that the underlying raw score metric must therefore be interval? This is critically important as most scales used in health studies are not subjected to Rasch analysis, but if a paper has been published that states that raw scores for an instrument are at the interval level, then arithmetical operations and statistical analyses for that instrument will be based on the original untransformed raw-score scale."

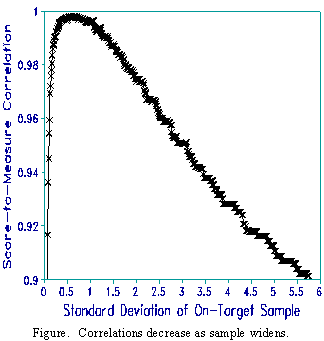
Response: If there are no missing data, then there is one logit measure corresponding to each possible raw score. Plotting one against the other will produce a monotonically increasing ogive. Further, if there is not much of the sample in the tails of the ogive, then the score-to-measure Pearson correlation will be about 1.0 (see Figure). The reason that raw scores "sort of work" is that the score-to-measure ogive usually has a straightish piece in the center. But, unless you do a Rasch analysis, you do not know:

(a) the precision (S.E.'s) of each score [but these are usually ignored and the raw scores analyzed as though they are exact, precise measures];

(b) which response strings make no sense (i.e., there is no quality control);

(c) which scores are not on the straightish part, for which analysis of raw scores is definitely misleading;

(d) whether the items in the instrument cooperate together to actually measure anything (the hierarchical item ordering and fit);

(e) whether the rating scale is being used as intended (the step parameters and fits).

Another fallacious argument is that "when raw scores correlate more highly with outcomes, they are better than Rasch measures". This capitalizes on local similarities between the curvature of raw scores and the characteristics of the sample. A prime example of this way of thinking is Grade Point Average (GPA). GPA correlates perfectly with average achievement across grades, but is notoriously non-linear (RMT 3:2, p. 60). To discover whether students are learning faster or slower in the higher grades we must use a measurement system that separates the details of the sample from the working of the measuring instrument.

Consider physical science: the spacing of the markings on a measuring rod is established independently of how the markings will be made (the test items) and is not biased by specifics of what is to be measured (the subjects).

Treating raw scores as interval measures is like driving in the fog: if the road is straight, you can succeed, but it's slow and difficult. It's easy to drift off the road or take a wrong turn without knowing it, and, if there's anything coming the other way, the outcome can be catastrophic.

John Michael Linacre

Linacre J.M. (1998) Do Correlations Prove Scores Linear? Rasch Measurement Transactions 12:1 p. 605-6.

Do Correlations Prove Scores Linear? Linacre J.M. … Rasch Measurement Transactions, 1998, 12:1 p. 605-6.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt121b.htm

Website: www.rasch.org/rmt/contents.htm