Two-Item Testing

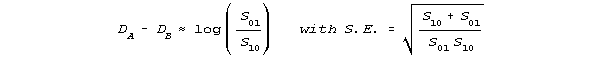
What is the shortest useful test? Here is how a test as short as two items can be productive. Imagine that a large sample of people have taken two dichotomous items, A and B, approximately as the Rasch model predicts. Here is the tabulation of their scored responses:

		Item B		Totals:
		Right: 1	Wrong: 0
Item A	Right: 1	S11	S10	TA1
	Wrong: 0	S01	S00	TA0
Totals:		TB1	TB0	T

According to the Rasch model, the difference between the item difficulties is estimated directly by

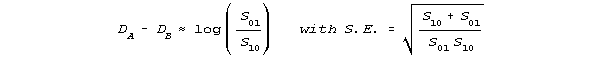
The sample distribution does not appear! Here is an immediate and useful application of the wonderful and essential sample-distribution-free consequence of the model.

If we think that the sample is normally distributed, then we can estimate the sample mean and standard deviation. The sample mean ability is relative to the average difficulty of the two items. A simulation study suggests the following estimator:

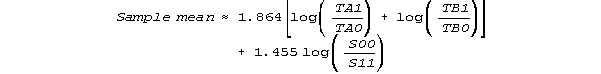
An estimator for sample standard deviation is:

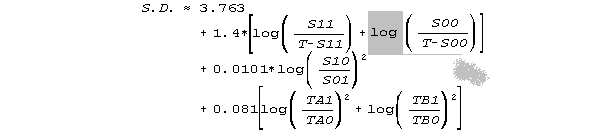
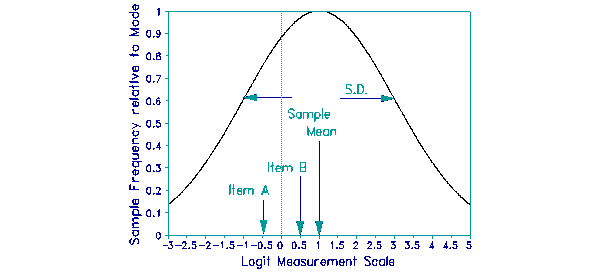
Suppose a normally distributed sample with mean of 1 logit and S.D. of 2 logits, (as shown in the Figure), take a test comprising two dichotomous items. The results for 1,000 examinees are shown in the Table:

Then, the difference between the difficulties of items A and B is log_e(81/221) = -1.0 logits. Item A is easier than Item B.

The sample mean is 1.864*[log_e(715/285) + log_e(575/425)] + 1.455*log_e(204/494) 1.0 logits above the mean of the items. So, if the local origin is set at the item mean, Item A is -0.5 logits difficult, Item B is at +0.5 logits, and the sample mean is at +1.0 logits.

The sample standard deviation is 3.763 + 1.4*[log_e(494/(1000-494)) + log_e(204/(1000-204))] + 0.101*log_e²(221/81) + 0.081*[log_e²(715/285) + log_e²(575/425)] = 2.0 logits. These results are shown in the figure on the previous page.

For tests of more than two items, compute these values for every combination of two items and average them.

If the two items had been previously anchored in a general item bank at D₁ and D₂, then the location of this sample, in the bank's frame of reference, is given by the linear transformations:

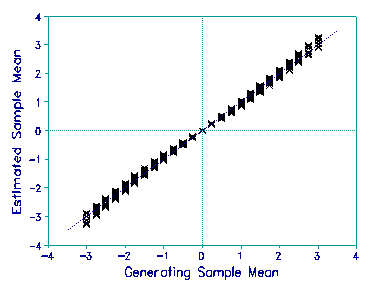
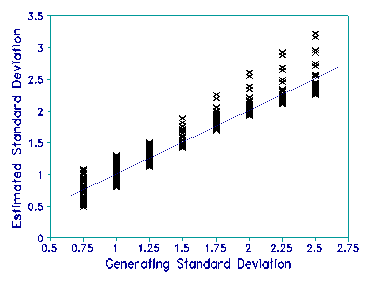
The overall success of recovering generating values in a simulation study is shown in the plots on this page. Data were simulated with a reasonable range of sample means and S.D.s, and also a reasonable range of item difficulties.
Benjamin D. Wright

Two-item testing? Wright B.D. … Rasch Measurement Transactions, 1998, 12:2 p. 627-8.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt122b.htm

Website: www.rasch.org/rmt/contents.htm