Rating, Judges and Fairness

Many types of performances require observers or "judges" to rate their quality: essays, spoken language, artistic and athletic activities, beauty contests, dog shows, science fairs. The construction of accurate measures from those ratings requires the judges to rate in valid ways. Tainted ratings can result from personal biases, idiosyncratic use of categories, and pressure to conform.

Judge training and assigning two or more judges to rate each performance are steps towards improving the quality of the ratings - but they are not an automatic solution to rating quality problems.

If disagreement is not permitted, then the judges are required to act as interchangeable "scoring machines", in much the same way as multiple optical scanners are used to scan forms for a large-scale MCQ test. This was long thought to be the ideal, and judge training focussed on unanimity: every judge must award the same rating to a particular performance. In practice, this ideal is never attained, no matter how much the judges are trained (brain-washed).

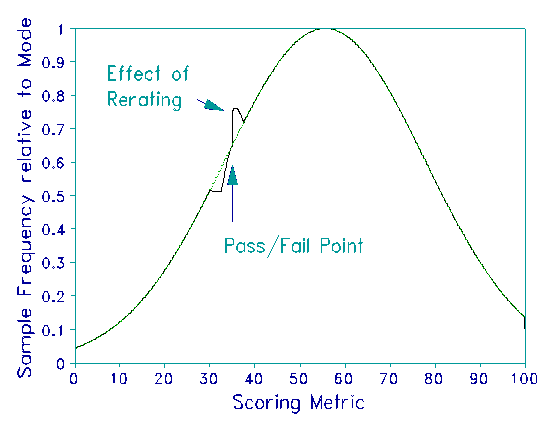
Rerating is one attempt to deal with judging deficiencies. If a "first prize" is to be awarded based on ratings, then the top ten performances may be rated several more times in order to try to assure that the best performance wins. If there is a criterion pass-fail point, then performances just below that level may be rerated and awarded the higher of the two sets or ratings. The British examination system uses this approach, producing a characteristic notch and bump in the performance distribution (see Figure).

If all ratings are equally crucial, then a system of paired judging is commonly used. Every performance is rated by two judges. Any disagreement of more than one rating point is resolved by having the performance rated by a third judge. Thus judge disagreement causes extra work for the judge panel. If judges disagree too much, one or both may be removed from the judging panel as "unreliable". This induces judges to minimize the risk of disagreement by increasing the chance that they agree. The implicit rule becomes, "when in doubt, avoid extreme categories". Disagreement of more than one category is less likely, or even impossible in many cases, when both judges use central categories. The overall effect is to promote conformity and to reduce the flow of possibly useful information among ratings. This produces an almost Guttman pattern of responses. When this type of data is submitted to Rasch analysis, it results in a scale for which the rating category steps are far apart. But linear measurement and fairness have been abandoned. Ratings given by two severe judges are considered numerically comparable to ratings given by two lenient judges, provided there is no gross disagreement within the pairs of judges.

From a Rasch viewpoint, the fact that raters know that agreement is preferable constrains their independence (each rater also considers the other rater when assigning a rating) and leads to deterministic features in the data. The Rasch analysis adjusts for this determinism by calibrating the rating scale category steps to reflect the amount of random behavior actually observed in the data. Since the randomness is small, the rating category steps are far apart. This induces an artificial security in the reported results. The rating scale is reported to be "highly discriminating", and the ordering of the performances is considered "highly reliable". But all this is illusory. The constraint of forced agreement has mandated it.

From the Rasch viewpoint, each judge is expected to rate independently of the other judges, but from the same point of view. "Independently" implies that judges are expected to exhibit some level of disagreement about the ratings to be awarded. Part of this disagreement is systematic, due to the different levels of leniency of judges. Part is stochastic, due to the myriad tiny factors that combine together to produce the observed rating. Judging "from the same point of view" implies that the judges understand the rating task and apply the rating scale in the same way.

The simplest aspect of this to verify is the use of the rating scale. Do judges encountering equivalent samples of performances award the rating scale categories with approximately the same frequencies? Avoidance of extreme categories is immediately obvious. Rasch rating scale statistics provide precise diagnosis of flaws in the use of individual categories. When judges rate a number of items on each performance (analytic rather than holistic rating), then rater-item interactions can be investigated.

If the judging plan includes a judge-linking network, then differences in judge leniency can be measured and adjusted for. Linking can be achieved by rotating judge pairings, or by having all judges perform some common tasks, such as rating videotapes or reading benchmark essays. Even without linking, the judging plan may assign candidates at random to judges. Judge severity can then be computed on the basis that the rated performances are randomly equivalent.

It is has been observed that ratings collected according to Rasch measurement ideals are computed to be less reliable than conventional paired ratings. But Rasch measurement has not degraded the data! Rather, Rasch measurement is giving an honest report on the validity of the rating process. The implicit constraints in conventional rating procedures, along with analysis of ratings as though they were point estimates on linear metrics, misleads the analyst into regarding the data points as more precise than they really are. Under those circumstances, a reported high reliability reflects highly replicability in the way judges award ratings, not high replicability of the performances themselves.

The Rasch analysis more honestly reflects the unevenness even within performances and the vagaries of even expert observers' impressions. It is only after these are honestly addressed that real improvements in the measurement of performances can result.
John Michael Linacre

Rating, judges and fairness.Linacre J.M. … Rasch Measurement Transactions, 1998, 12:2 p. 630-1.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt122f.htm

Website: www.rasch.org/rmt/contents.htm