When modeling the responses to true-false questions and minimum-competency MCQ, it may be useful to impose a lower asymptote on the dichotomous Rasch model. This lower asymptote is not established by a parameter to be estimated, but is defined by the construction of the test items.
Suppose that ki, a constant, is the probability that a respondent of infinitely low ability will select the "correct" answer to question i, of difficulty di. Then the Rasch model for the probability, Pni, of a correct response by person n of ability bn is:
The proportion correct, pr, for a person with r correct answers out of L is:
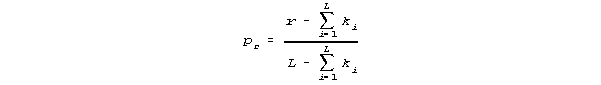
and the proportion correct, pi for item i, answered correctly by si persons out of N is
These proportions can be used directly in the PROX formulae (Best Test Design, Wright & Stone, 1979, chapter 2):
where
and the expansion factors, X and Y, are given by
John M. Linacre
PROX for guessing.Linacre J.M. … Rasch Measurement Transactions, 1998, 12:3 p. 655.
| Rasch Publications | ||||
|---|---|---|---|---|
| Rasch Measurement Transactions (free, online) | Rasch Measurement research papers (free, online) | Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch | Applying the Rasch Model 3rd. Ed., Bond & Fox | Best Test Design, Wright & Stone |
| Rating Scale Analysis, Wright & Masters | Introduction to Rasch Measurement, E. Smith & R. Smith | Introduction to Many-Facet Rasch Measurement, Thomas Eckes | Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr. | Statistical Analyses for Language Testers, Rita Green |
| Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar | Journal of Applied Measurement | Rasch models for measurement, David Andrich | Constructing Measures, Mark Wilson | Rasch Analysis in the Human Sciences, Boone, Stave, Yale |
| in Spanish: | Análisis de Rasch para todos, Agustín Tristán | Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez | ||
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 25 - March 8, 2023, Wed..-Wed. | On-line course: Introductory Rasch Analysis (M. Horton, RUMM2030), medicinehealth.leeds.ac.uk |
| Apr. 11-12, 2023, Tue.-Wed. | International Objective Measurement Workshop (IOMW) 2023, Chicago, IL. iomw.net |
| June 23 - July 21, 2023, Fri.-Fri. | On-line workshop: Practical Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
| Aug. 11 - Sept. 8, 2023, Fri.-Fri. | On-line workshop: Many-Facet Rasch Measurement (E. Smith, Facets), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt123k.htm
Website: www.rasch.org/rmt/contents.htm