Turbo Pascal Measurement Program

Comas M, Vilagut G, Prieto L.

The following application, programmed in Turbo Pascal, is intended to automate the estimation of measures with known polytomous item difficulties using the method proposed by Linacre (1998):

(Eq. 1)

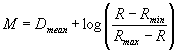(Eq. 2)

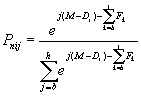(Eq. 3)

(Eq. 4)

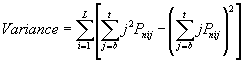(Eq. 5)

(Eq. 6)

The Turbo Pascal routine was initially developed to be applied to the responses of the VF-14 questionnaire. The VF14 measures functional capacity related to vision based on 14 daily life activities (items) affected by cataracts (Steinberg, 1994). Patients rate their difficulty doing each activity (0 "no difficulty" to 4 "unable"), final scores ranging from 0 (worst) to 100 (best). The item and step difficulties of the VF-14 were calibrated in a sample of 198 Spanish patients participating in an International study.

The specific parts of the routine related to this VF-14 are written in bold italics and must be replaced in case of using any other instrument.

PROGRAM RASCHVF14 (INPUT,OUTPUT);

CONST MIN=0; {minimum category of responses}

MAX=4; {maximum category of responses}

MAXI=14; {number of items}

MAXCAT=5; {number of response categories}

TYPE ITEMS = ARRAY [1..MAXI] OF REAL; {structure for item information}

CATEG = ARRAY [1..MAXCAT] OF REAL; {structure for category information}

PROB = ARRAY [1..MAXI] OF CATEG; {matrix of probabilities (MAXI x MAXCAT)}

CONST D:ITEMS=(1.27,0.48,-1.47,-1.58,-0.35,-0.13,0.64,0.26,-0.67,-0.5,-1.32,
-0.38,1.41,2.33); {difficulty measures of items. Insert your own item difficulties}

STEPS:CATEG=(0,-0.42,-0.49,0.98,-0.07); {steps for categories. Insert your own steps}

VAR R,Dmean,M,M2,SCORE,V:REAL; L:INTEGER; PUNT,DP:ITEMS; P:PROB;{R = Raw Score; Dmean = mean of difficulty measures of the answered items}

{M = M; M2 = M updated; SCORE = Score; V = variance of Rasch measurement}

{L = number of answered items; PUNT = array of responses}

{DP = array of difficulty measures of the answered items}

{P = matrix of probabilities}

{Initialization of variables}

PROCEDURE INITIALIZE(VAR R,M,M2:REAL;VAR L:INTEGER;VAR DP,PUNT:ITEMS;VAR P:PROB);

VAR I,J:INTEGER;

BEGIN

R:=0;M:=0;M2:=0;L:=0;

FOR I:=1 TO MAXI DO

BEGIN

PUNT[I]:=9; {the array of responses is initialized as missing

values}

DP[I]:=0; FOR J:=1 TO MAXCAT DO P[I][J]:=0;

END

END;

{Reads responses from keyboard and computes Dmean}PROCEDURE READ_INPUT(VAR PUNT,DP:ITEMS;VAR L:INTEGER;VAR Dmean:REAL);

VAR I:INTEGER;

P:ITEMS;

SUMADI:REAL;

BEGIN

L:=0;

SUMADI:=0;

FOR I:=1 TO MAXI DO

BEGIN

IF ((P[I]>=MIN) AND (P[I]<=MAX)) THEN

BEGIN

L:=L+1; {number of valid responses}

PUNT[L]:=MAX-P[I]; {Rescoring of initial responses of VF-14}

DP[L]:=D[I]; {array with difficulty measures of the
answered items}

SUMADI:=SUMADI+D[I]; {sum of difficulty measures}

END;

END;

IF L<>0 THEN Dmean:=SUMADI/L; {computation of the average item difficulty.
Eq. 1}

END;

{Computation of Raw Score R}

PROCEDURE RAW_SCORE_M(VAR R,M:REAL;Dmean:REAL;PUNT:ITEMS;L:INTEGER);

VAR I,Rmin,Rmax:INTEGER;

BEGIN

I:=1;

FOR I:=1 TO L DO R:=R+PUNT[I];

Rmin:=MIN*L;

Rmax:=MAX*L;

IF R=Rmin THEN R:=R+0.5;

IF R=Rmax THEN R:=R-0.5;

M:=Dmean+LN((R-Rmin)/(Rmax-R)); {Eq. 2}

END;

{Computation of the matrix of probabilities and M}

PROCEDURE PROBABILITIES(VAR P:PROB;PUNT,DP:ITEMS;M:REAL;VAR SCORE,V,M2:REAL;L:INTEGER;R:REAL);

VAR I,J:INTEGER;

F,DEN,EXP2,E2XP,E:REAL;

NUM:CATEG;

DIF:ITEMS;

BEGIN

FOR I:=1 TO L DO FOR J:=1 TO MAXCAT DO P[I][J]:=0;

SCORE:=0;

V:=0;

F:=0;

FOR I:=1 TO MAXI DO DIF[I]:=0;

FOR I:=1 TO L DO

BEGIN

F:=0;

DEN:=0;

FOR J:=1 TO MAXCAT DO NUM[J]:=0;

FOR J:=1 TO MAXCAT DO

BEGIN

F:=F+STEPS[J];

E:=((J-1)*(M-DP[I]))-F;

NUM[J]:=EXP(E);

DEN:=DEN+NUM[J];

END;

FOR J:=1 TO MAXCAT DO

BEGIN

P[I][J]:=NUM[J]/DEN; {Eq. 3}

SCORE:=SCORE+(J-1)*P[I][J]; {Eq. 4}

END;

END;

FOR I:=1 TO L DO

BEGIN

E2XP:=0;EXP2:=0;

FOR J:=1 TO MAXCAT DO

BEGIN

E2XP:=P[I][J]*SQR(J-1)+E2XP;

EXP2:=P[I][J]*(J-1)+EXP2;

END;

DIF[I]:=E2XP-SQR(EXP2);

V:=DIF[I]+V; {Eq. 5}

END;

M2:=M+((R-SCORE)/V); {Eq. 6}

END;

{Computation of Rasch measurement and its standard error and CI95%}

PROCEDURE RESULTS(M,V:REAL;VAR Q:CHAR;L:INTEGER);

VAR SE,PT,ICMIN,ICMAX:REAL;

BEGIN

SE:=0;

PT:=0;

ICMIN:=0;

ICMAX:=0;

IF L=0 THEN WRITELN('No valid responses')

ELSE

BEGIN

PT:=50.64+(11.75*M); {Rasch measurement on a 0 to 100 scale}

SE:=11.75*(1/SQRT(V)); {standard error}

ICMAX:=PT+1.96*SE; {upper confidence interval limit (CI95%)}

ICMIN:=PT-1.96*SE; {lower confidence interval limit (CI95%)}

{output:} WRITELN(PT:4:0,' (SE: ',SE:4:0,')');

WRITELN('IC: [',ICMIN:4:0,',',ICMAX:4:0,']');

END;

END;

{Main program}BEGIN INITIALIZE(R,M,M2,L,DP,PUNT,P); READ_INPUT(PUNT,DP,L,Dmean); IF L>0 THEN BEGIN

RAW_SCORE_M(R,M,Dmean,PUNT,L);

PROBABILITIES(P,PUNT,DP,M,SCORE,V,M2,L,R);

WHILE ABS(M2-M)>0.01 DO

BEGIN

M:=M2;

PROBABILITIES(P,PUNT,DP,M,SCORE,V,M2,L,R);

END;

END;

RESULTS(M,V,Q,L);

END.

REFERENCES

Alonso J, Espallargues M, Andersen TF, et al. International Applicability of the VF-14. An Index of Visual Function in Patients with Cataracts. Ophtalmology 1997; 104: 799-807.

Linacre JM. Estimating Measures with Known Polytomous Item Difficulties. Rasch Measurement Transactions 1998; 12: 638.

Prieto L, Alonso J, Valderas JM, et al. A Proposal of Content-Based Interpretation of Health-Related

Quality of Life Scores. Quality of Life Research 1998; 7: 652-653.

Steinberg EP, Tielsch JM, Schein OD, et al. The VF-14: an Index of Functional Impairment in Patients with Cataract. Archives of Ophtalmology 1994; 112: 630-638.

Turbo Pascal Measurement Program Prieto L, Comas M, Vilagut G … Rasch Measurement Transactions, 1999, 12:4 p.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt124i.htm

Website: www.rasch.org/rmt/contents.htm