MFORMS: one-step (concurrent) Item Banking and Concurrent Equating Computer Program

Persons concerned with item banking will be interested in a new computer program, MFORMS (Wright & Schulz, 1987). MFORMS is a derivative of MSTEPS (Wright, et al., 1986), and is similar to MICROSCALE (Wright and Linacre, 1985), in its ability to accommodate missing values in a data matrix.

The accommodation of missing values in MFORMS enables one to combine data from a network of multiple forms into a single matrix. The missing values in this matrix then arise because no one individual takes all of the items in all of the forms and no item is taken by all of the persons. This is the usual situation when building large item banks.

The data need not be submitted to MFORMS in the form of a large matrix with missing values, however. MFORMS can read records from multiple forms, and create its own internal matrix. The user must include a form-identification field in each record, and supply additional information that tells MFORMS the item-in-bank sequence number of each item-within-forms. MFORMS uses this information in two "../indexing" arrays.

The virtual memory needed by MFORMS to hold the data is less than would be needed to hold the large NI*NN matrix implied by all items (NI) and all persons (NN). MFORMS stores the data in NN*NIFORM bytes, where NIFORM is the maximum number of items per form.

MFORMS will accept initial estimates of item calibrations. This feature is particularly useful when the items cover two or more grade levels in an educational curriculum. Well chosen initial estimates enable the program to converge faster, as is shown in the following example.

The MFORMS program was used at the Chicago Public Schools to equate 960 test items covering the reading curriculum of grades 3 to 8. There were 160 items per grade level. A test linking network was set up for a total of 40 forms. Most forms were 40 items long, and contained 10 linking items. The remaining forms were 80 items long and contained 50 linking items. There were 8,496 records, 8,296 of which had non-perfect scores.

The virtual memory required by MFORMS to hold these data was 8496*80 (NN*NIFORM), or approximately 700K bytes. This is a critical savings of virtual memory, since about 8200K bytes (NN*NI) would be needed were there no indexing arrays in MFORMS. The indexing arrays in this case use 20K bytes. The total virtual memory used by MFORMS for this problem was 2760K.

The MFORMS program was used on the above data with three sets of initial item calibrations, corresponding to three sizes of expected difference between adjacent grades. The default initial calibrations were set at 0.0 logits between grades. That is, all items begin with 0.0. The other initial calibrations set differences of 0.5 logits or 1.0 logit between grades. With 0.5 logits difference, grade 3 items and grade 8 items were initialized at -1.25 and +1.25 logits respectively. With 1.0 logits difference, grade 3 and grade 8 items were set at -2.5 and +2.5 logits respectively. Intermediate grade levels had intermediate initial values.

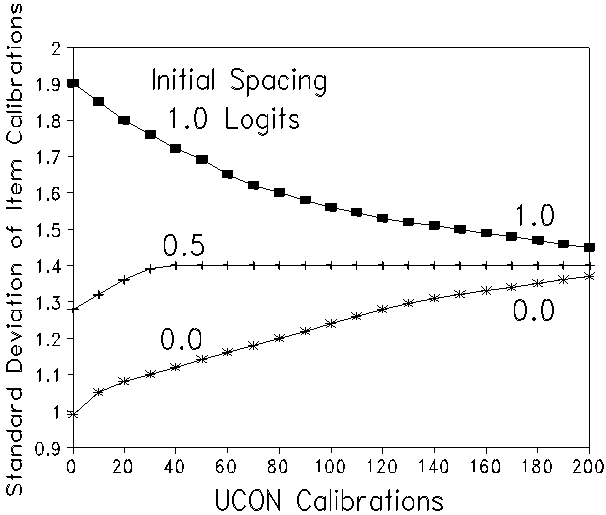
The MFORMS program took approximately 35 seconds of IBM 3033 CPU per JMLE (UCON) iteration. With initial calibrations of -1.25 to +1.25 logits, (0.5 logits between grade levels), the standard deviation of item calibrations reached 1.396 logits (N=960) on the 167th iteration, and remained there through the 300th iteration. Rounding, the standard deviation of items reached 1.4 on the 26th iteration, and 1.40 on the 131st iteration. The CPU times necessary to bank these items to accuracies of 1.4, 1.40, and 1.396, were 18.2 minutes, 78.5 minutes, and 98.2 minutes. The mean standard error of item calibration was 0.14 logits.

When no initial calibrations were provided, the standard deviation of items reached a rounded value of 1.4 on the 188th iteration, and had not reached 1.40 by the 250th iteration. When initial calibrations were 1.0 logits between grade levels (-2.5 to +2.5), the program reached 1.4 by the 180th iteration, but had not reached 1.40 by the 250th iteration.

Figure 1.

Figure 1 shows the plot of item standard deviations against UCON iterations for these three sets of preset calibrations. The advantage of supplying initial calibrations for one-step (concurrent) item banking with MFORMS is clear. With an initial difference of 0.5 logits between grade levels, the spread of item calibrations reaches a stable value sooner.

Regardless of whether initial item calibrations are provided, one-step (concurrent) item banking via the MFORMS, MSCALE, or MSTEPS programs offers the following advantages over multistep procedures of item banking: 1) simultaneous use of all the data bearing on a person measure or item calibration, 2) savings of man-hours, and 3) reduction of potential for error. The advantage of simultaneously using all the data bearing on parameter estimates is discussed by Kelderman (1986). Man hours are saved, in this case, by combining 40 separate Rasch analyses (40 forms) into one and eliminating the need for secondary analyses to compute and apply translation constants between forms. The potential for human error is reduced with a reduction in the time and handling of data needed to equate the items.

MFORMS is unique, however, in the following respects: 1) it takes less virtual memory to store the data, 2) it reads data from multiple forms and sets up the data matrix, and 3) it accepts initial estimates for the item calibrations, thereby reducing the CPU time necessary to reach convergence. MFORMS is available for IBM-compatible and DEC- compatible main- frame computers.

Kelderman, H. (1986). Common Item Equating Using the Loglinear Rasch Model (Research Report 86-9). Enschede, Netherlands: University of Twente, Department of Education, Division of Educational Measurement and Data Analysis.

Wright, B.D. and Linacre, J.M. (1985). MICROSCALE. Westport: MEDIAX.

Wright, B.D. and Schulz, E.M. (1987). MFORMS [A FORTRAN computer program for one-step (concurrent) item banking of dichotomous and partial credit data from multiple forms]. Chicago IL: MESA Press.

Wright, B.D., Schulz, E.M., Congdon, R.T. and Rossner, M. (1987) MSTEPS [A FORTRAN computer program for Rasch analysis of dichotomous and partial credit data]. Chicago IL: MESA Press.

Computer programs: MFORMS for one-step (concurrent) item banking and concurrent equating. Schulz EM. … Rasch Measurement Transactions 1:2 p.10-11

Computer programs: MFORMS for one-step (concurrent) item banking. Schulz EM. … Rasch Measurement Transactions, 1988, 1:2 p.10-11

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt12b.htm

Website: www.rasch.org/rmt/contents.htm