θ is hypothesized, but not estimated.
Are Rasch models merely an area within item response theory (IRT) or do they embody a distinctly different philosophical approach? Superficially, the answer appears obvious. Rasch is part of IRT. Indeed, Rasch models are central to thirteen of the twenty-eight chapters of the Handbook of Modern Item Response Theory (HMIRT, Wim J. van der Linden & Ronald K. Hambleton, Eds., New York: Springer, 1997).
"The central feature of item response theory (IRT) is the specification of a mathematical function relating the probability of an examinee's response to a test item to an underlying ability. ... In the 1940s and 1950s, the emphasis was on the normal-ogive response function, but for statistical and practical reasons this function was replaced by the logistic response function in the late 1950s" (HMIRT, p. v).
This quotation from the opening paragraph to the Preface of HMIRT hints at a more profound answer. IRT is a descriptive methodology. It hunts for convenient mathematical functions to describe a situation. If more "practical" mathematical functions were to be discovered, that are also "statistically tractable" (p. 4), then the logistic response function, including Rasch, would be relegated in the next edition of HMIRT to the same prominence that the normal-ogive function enjoys in this edition, i.e., one chapter.
"... IRT started out as an attempt to adjust test scores for the effects of such nuisance properties of test items as their difficulty, discriminating power, or liability to guessing. Realistic models with parameters for each of these effects were needed" (p. 22).
Now we are starting to identify substantive conceptual differences between Rasch and IRT. Are differences in item difficulties a "nuisance property"? According to Georg Rasch (1960, p. 72) "we must be able to confront the persons with a battery of test problems, preferably of widely varying difficulty, which can act as a measuring instrument." It is the differences in item difficulty (or their extension into rating scale categories) which define what is being measured. This is supremely "practical" and "realistic", yet is almost ignored in HMIRT. Only Susan Embretson, in Chapter 18 on Rasch "Multicomponent Response Models" mentions construct validity, i.e., are we measuring what we think we are measuring?
But how does IRT relate to measurement?
HMIRT makes a promising first step: "Long experience with measurement instruments such as thermometers, yardsticks, and speedometers may have left the impression that measurement instruments are physical devices providing measurements that can be read directly off a numerical scale. This impression is certainly not valid for educational and psychological tests. A useful way to view a test is as a series of small experiments in which the tester records a vector of responses by the testee. These response are not direct measurements, but provide the data from which measurements can be inferred" (p. 1).
At this point, the reader of HMIRT would expect a discussion of the measurement properties of thermometers (e.g., Choppin 1985) touching on linearity, additivity, objectivity, separability, sufficiency, and their "sample-free" and "test-free" properties. This would be followed by a discussion of how such measures can be inferred from ordinal observations, i.e., what models support parameters with those properties (e.g., RMT passim). But the reader with these expectations will be disappointed.
No discussion whatsoever of measurement principles is presented - not even a definition. The reader is lead to believe that all parameter estimates for every model described in HMIRT are automatically constructed in a linear frame of reference and have equal stability and usefulness. IRT is concerned with controlling errors, not constructing measures.
"The methodological problem of controlling responses for experimental error holds for tests. ... Unless adequate control is provided for such [background, nuisance or error] variables, valid inferences cannot be made from the experiment" (p. 1). Accordingly the very first model presented in HMIRT is the "true score" model of classical test theory (CTT). It is criticized, not for the non-linearity of its parameters, but because "true" scores cannot be generalized across different tests. "The reason is that each test entails its own sets of items and that each item has different properties. From a measurement point of view, such properties of items are nuisance or error variables that escape standardization" (p. 3, emphasis theirs).
IRT still yearns for the classical ideal of no error, no unexplained randomness. Rasch, in contrast, insists on "models which are indeterministic, where chance places a decisive role" (1960, p. 11, his emphasis).
"Each [of 27 chapters] in this book contains an up-to-date description of a single IRT model (or family of models) written by the author(s) who originally proposed the model or contributed substantially to its development" (p. v). Chapters follow a simple outline: Introduction, Presentation of the Model, Parameter Estimation and Goodness of Fit, a brief Empirical Example, and sometimes a Discussion. This does make HMIRT a useful reference work for the mathematics of the less familiar models.

|
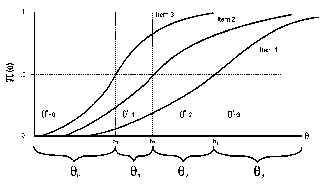
| Mokken's Figure 3. Double monotonicity. θ is hypothesized, but not estimated. |
For instance, Mokken scaling is often lumped with Rasch scaling because it is built on many of the same specifications. In Chapter 20, Robert J. Mokken describes his own model. It is based on Guttman ordering. If every item generates an equivalent order of person abilities, then the items have monotonic homogeneity. If, simultaneously, every person generates an equivalent order of item difficulties, then the items have double monotonicity, i.e., conjoint transitivity or Guttman ordering (see Figure above). Of course, monotonicity is rarely observed in practice, but, Mokken reports, "experience based on a few decades of numerous applications has shown that in practice [weak ordering] performs quite satisfactorily, delivering long and useful scales" (p. 361). This is encouraging, because, according to Mokken's criteria, Rasch scales are weakly ordered or better. The result could scarcely be otherwise, because weakly-ordered double homogeneity, otherwise known as probabilistic Guttman ordering, requires data which fit the Rasch model (RMT 6:2, 232).
Since Mokken scaling is non-parametric, it does not estimate person or item measures. So what are used?
(a) Raw scores, "an optimal statistic for various types of classification" (p. 358) - but Mokken fails to mention that these are non-linear. It is the Rasch model that converts raw scores to linear measures (RMT 3:2 62).
(b) The first principal component of the correlations in a matrix of weighted responses. For one weighting scheme, Mokken remarks that "This type of scoring seems intuitively satisfactory: Answering a difficult item correctly contributes heavily to the total score, whereas an incorrect response is not penalized too much" (p. 359). Let's hope they don't use this for driving tests and brain surgeons!
[Mokken references are listed below.]
In the context of the standard chapter format, the philosophical and practical attributes of the Rasch models sound much like those of the other models. The section introductions reinforce this. "The steps model by Verhelst, Glas and de Vries (Chap. 7), the (independently developed but formally identical) sequential model for ordered responses of Tutz (Chap. 8), the generalized partial credit model of Muraki (Chap. 9), and the partial credit model of Masters and Wright (Chap. 6) are variations of Samejima's graded response model [(Chap. 5)] ..., [but] the rating scale model of Andersen (Chap. 4) [was] developed as an extension of the Rasch model" (p. 30). Surely every one of these authors was amazed to read this taxonomy, and surely David Andrich was equally amazed to be omitted from it. In fact, all these models are Rasch models except for the unrelated models of Muraki and Samejima.
A virtue of HMIRT, however, is that less familiar Rasch models are presented. For instance, "Multiple-Attempt, Single Item Response Models" (MASI, Judith A. Spray, Chap. 12) are binomial trials models in which the number of successes, rather than the number of trials, are fixed. As always, it is the ratio of successes to failures that is key. MASI, however, invites distinctive applications. In educational applications, a one-success form of this model is "answer until correct". In sport's applications, it measures psychomotor ability.
John Michael Linacre
Choppin BHL. 1985. Lessons for psychometrics from thermometry. Evaluation in Education (now Internal Journal of Educational Rsearch), 9:1, 9-12.
Meditations on the Handbook of Modern Item Response Theory Linacre, J.M. … Rasch Measurement Transactions, 1999, 13:2 p. 690
Courtesy of Teresa Rivas Moya (1999) Ajuste del Modelo de Mokken con el Programa MSP 4.0: Una Aplicacion con Items de Razonamiento Inductivo Numerico. Revista Electrónica de Metodología Aplicada, 4, 2, 37-70
Ellis, J.L. & Wollenberg, A.L. van den (1993). Local Homogeneity in latent trait models. A characterization of the homogeneous monotone IRT model. Psychometrika, 58, 417-429.
Gifi, A. (1990). Nonlinear Multivariate Analysis. New York: Wiley
Grayson, D.A. (1988). Two-group classification in latent trait theory: Scores with monotone likelihood ratio. Psychometrika, 53, 383-392.
Guttman, L. (1945). A basis for analyzing test-retest reliability. Psychometrika, 10, 255-282.
Guttman, L. (1950). The basis for scalogram analysis. In S.A. Stouffer, L. Guttman, E.A., Suchman, P.F., Lazarsfield, S.A. Star, & J.A. Clausen (Eds.), Measurement and prediction. Princeton: Princeton University Press.
Lord, F.M. (1980). Applications of item response theory to practical testing problems. Hillsdale, New Jersey: Erlbaum.
Martínez, M. R. & Rivas, T. (1990). Análisis de escalas acumulativas: Modelo Probabilístico de Mokken para items dicotómicos. Psicothema, 3, 199-218.
Meijer, R.R., Sijtsma, K. & Smid, N.G. (1990). Theorical and empirical comparison of the Mokken and the Rasch approach to IRT. Applied Psychological Measurement, 14, 283-298.
Mokken, R.J. (1971). A Theory and procedure of scale analysis. The Hague: Mouton.
Mokken, R.J. (1997). Nonparametrics models for dichotomous responses. En W.J. van der Linden & R.K. Hambleton (Eds.). Handbook of Modern Item Response Theory. New York: Springer.
Mokken, R.J. & Lewis, C. (1982). A nonparametric approach to the analysis of dichotomous item responses. Applied Psychological Measurement, 6, 417-430.
Mokken, R.J., Lewis, C. & Sijtsma, K.(1986). Rejoinder to "The Mokken scale: A critical discussion". Applied Psychological Measurement, 10, 279-285.
Molenaar, I.W. (1982). Mokken scaling revisited. Kwantitatieve Methoden, 3, 145-164.
Molenaar, I.W. (1983). Rasch, Mokken and school experience. In S. Lindenberg & F.N. Stokman (Eds.) Modellen in the Sociologie. Deventer: Van Loghum Slaterus.
Molenaar, I.W. (1986). An exercise in item response theory for three ordered response categories. In G.F. Pikkemaat, & J.J.A. Moors (Eds.), Liber amicorum Jaap Muilwijk. Groningen: Econometrisch Institut.
Molenaar, I.W., Debets, P., Sijtsma, K. & Hemker, B.T. (1994). MSP 4.0: A program for Mokken Scale Analysis for Polytomous Items. Groningen: Iec ProGAMMA.
Molenaar, I.W. & Sijtsma, K. (1984). Internal consistency and reliability in Mokken's nonparametric item response model. Tijdschrift voor Onderwijs-research, 9, 257-268.
Molenaar , I.W., Sijtsma, K., Van Schuur, W.H. & Mokken, R.J. (1999). MSPWIN 5.0: A program for Mokken Scale Analysis for Polytomous Items. Groningen: Iec ProGAMMA.
Rivas, T. & Martinez, M. R. (1992). MOKPAS: Un programa para el escalamiento de items según el modelo TRI no paramétrico de Mokken. Investigaciones Psicológicas, 187-205.
Rivas, T., Martinez, M. R. & Hidalgo, R. (1996). MOKFOR1: A program to fit an accumulative scale to Mokken non parametric IRT model. 20th Biennial Conference of the Society for Multivariate Analysis in the Behavioral Sciences, ESADE, Barcelona.
Rosenbaum, P.R. (1984). Testing the conditional independence and monotonicity assumptions of item response theory. Psychometrika, 49, 425-435.
Rosenbaum, P.R. (1987). Comparing item characteristic curves. Psychometrika, 52, 217-233.
Sijtsma, K. (1998). Methodology Review. Non parametric IRT approaches to the analysis of dichotomous item scores. Applied Psychological Measurement, 22, 3-31.
Sijtsma, K. & Meijer, R.R. (1992). A method for investigating the intersection of item response functions in Mokken's noparametric IRT model. Applied Psychological Measurement, 16, 149-157.
Sijtsma, K. & Molenaar, I.W. (1987). Reliability of test scores in nonparametric item response theory. Psychometrika, 52, 79-97.
Torgerson, W.S. (1958). Theory and methods of Scaling. New York: Wiley.
| Forum | Rasch Measurement Forum to discuss any Rasch-related topic |
Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement
Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.
| Coming Rasch-related Events | |
|---|---|
| Jan. 16 - Feb. 13, 2025, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| Apr. 8 - Apr. 11, 2026, Wed.-Sat. | National Council for Measurement in Education - Los Angeles, CA, ncme.org/events/2026-annual-meeting |
| Apr. 8 - Apr. 12, 2026, Wed.-Sun. | American Educational Research Association - Los Angeles, CA, www.aera.net/AERA2026 |
| May. 15 - June 12, 2026, Fri.-Fri. | On-line workshop: Rasch Measurement - Core Topics (E. Smith, Winsteps), www.statistics.com |
| June 19 - July 25, 2026, Fri.-Sat. | On-line workshop: Rasch Measurement - Further Topics (E. Smith, Winsteps), www.statistics.com |
The URL of this page is www.rasch.org/rmt/rmt132d.htm
Website: www.rasch.org/rmt/contents.htm