Understanding (or Misunderstanding?) the Rasch Model

"Item Response Theory: Understanding the One-Parameter Rasch Model" is the perplexing title of a chapter by Catherine E. Cantrell in B. Thompson (Ed.) Advances in Social Science Methodology. Vol. 5. (Stamford, CT: JAI Press, 1999, p. 171-191).

The good news is that 15 of the 21 pages of this chapter are devoted to a Rasch analysis of a complete, but anonymous, dichotomous data set in which 36 people take an 18 item test. Could this be another administration of our old friend the Knox Cube Test (Wright & Stone, 1979)? Dare we hope that Social Science methodology has now advanced to 1979?

The best section in the chapter is too short. It is entitled "Evaluating Model Invariance". "To test whether the final item calibrations are truly person independent, researchers may choose to do a cross validation. By tradition, this is typically done by dividing persons in a large sample with a large spread into six ability groupings (e.g., extremely high ability, moderately high ability, ...). Item calibrations are then computed separately for each group. If the item calibrations ... are similar ..., then there is fairly compelling evidence that the final calibrations are sample independent." (p. 189) What a great tradition! (Why have I never heard of it before?) If followed, all other approaches would be crushed by the Rasch juggernaut, and there truly would be a giant advance in social science methodology.

The bad news in this chapter is that foundational concepts of Rasch and IRT are muddled. Here are some misconceptions, worth noting because our diligent, but unseasoned, author is probably not alone in them.

The Rasch model is explained to be a one-parameter IRT model in which "both guessing and item discrimination parameters are considered negligible, and therefore these influences are not modeled" (p. 174). In fact, with the Rasch model, guessing is not considered "negligible", it is considered a serious threat to measurement validity. It is conspicuously flagged for attention by the analyst. Item discrimination can never be "negligible"! For construct stability, item discrimination must be constant. Rasch analysis detects and reports deviation of item discrimination from this ideal.

"The fit of the model to the data must be evaluated ..., and not simply assumed." (p.187, author's emphasis). Wise advice, but better stated in a Rasch measurement context as "The fit of the data to the model ...".

"According to the [Rasch or] IRT model, if there were perfect model fit, everything to the left of the line [responses to the easier items] should be correct, denoted 1. Everything to the right [responses to the harder items] should be incorrect, denoted 0." (p. 187) But this is not perfect fit to a probabilistic model. It is Guttman's deterministic ideal. For Rasch and IRT models, perfect fit requires some failures on easier items and some successes on harder items.

"In fact, all items and persons found to be statistically significant are removed from the data and the entire analysis is repeated iteratively ... until no items or persons deviate to a statistically significant extent from the model" (p. 189). Since the Rasch model is the expression of an unreachable (but essential and useful) ideal, no data ever fit it perfectly. Consequently, it is not unusual to eliminate all the items and persons if this iterative procedure is followed! It is as though we peeled an onion to find the perfect core - only to be left with no onion at all! We have to stop the iterative procedure when the measures are good enough for the purposes they are intended - whatever the significance tests say.

"Lawson (1991) and Fan (1998) have both raised serious concerns about how substantial these advantages [of IRT and Rasch] are (or how bad the classical model results are).... classical and Rasch yielded almost perfectly correlated results. ... [For the author's sample,] the person abilities were again correlated using a regression analysis that yielded r =.997." (p. 189) Since the central part of the ogival model ICC is almost straight, a high correlation is expected between measures and raw scores for complete, on-target response patterns. But raw score analysis wilts when exposed to broader targeting, missing data, incoherent response patterns and test equating. Raw score analysis has little to say about construct validity, i.e., the item hierarchy, or predictive validity, i.e., the person hierarchy. Unfortunately, this chapter ignores these issues and fails even to mention that sine qua non of Rasch analysis, an item map. The author somewhat redeems herself with "although classical and Rasch parameters may be very similar (though scaled in different metrics), IRT theories and computer software do require the user to carefully examine aberrant data and make thoughtful decisions about which persons and what items should remain in the final calibration computations" (p. 191).

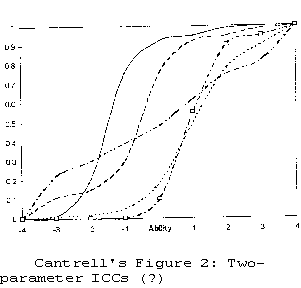
And finally, a curious plot of item characteristic curves: "Figure 2 presents ICCs from a two-parameter model. Note that the item characteristic curves are asymptotic to zero (i.e., intercept 0 at ability = -4)" (p.174). Asymptotic means that the curves approach, but never intercept their limits. Ogival ICCs can never dip below 0 probability, neither can they have little bumps nor sharp changes in direction. In Figure 2, the dotted ICC comes closest to a 2-PL ogive.

John Michael Linacre

Fan, X. (1998) Item response theory and classical test theory: an empirical comparison of their item/persons statistics. Educational and Psychological Measurement, 58, 357-381.

"I have just read an article by Fan comparing CTT and IRT. I am curious if anyone has read any other comparative pieces focusing primarily on the one-parameter Rasch model? If so, can you send me the reference?"

Stacie Hudgens

William P. Fisher, Jr., replies:

For other comparisons, especially given your health care interests, check out the following:

Fisher, W. P., Jr. (1993). Measurement-related problems in functional assessment. The American Journal of Occupational Therapy, 47(4), 331-338.

McHorney, C. A., Haley, S. M., & Ware, J. E. (1997). Evaluation of the MOS SF-36 Physical Functioning Scale (PF-10): II. Comparison of relative precision using Likert and Rasch scoring methods. Journal of Clinical Epidemiology, 50(4), 451-461.

Raczek, A. E., Ware, J. E., Bjorner, J. B., Gandek, B., Haley, S. M., Aaronson, N. K., Apolone, G., Bech, P., Brazier, J. E., Bullinger, M., & Sullivan, M. (1998). Comparison of Rasch and summated rating scales constructed from SF-36 physical functioning items in seven countries: Results from the IQOLA Project. Journal of Clinical Epidemiology, 51(11), 1203-1214.

Stucki, G., Daltroy, L., Katz, N., Johannesson, M., & Liang, M. H. (1996). Interpretation of change scores in ordinal clinical scales and health status measures: The whole may not equal the sum of the parts. Journal of Clinical Epidemiology, 49(7), 711-717.

van Alphen, A., Halfens, R., Hasman, A., & Imbos, T. (1994). Likert or Rasch? Nothing is more applicable than good theory. Journal of Advanced Nursing, 20, 196-201.

Zhu, W. (1996). Should total scores from a rating scale be used directly? Research Quarterly for Exercise and Sport, 67(3), 363-372.

In much the same vein, you might find these more technical source articles useful:

Andrich, D. (1989). Distinctions between assumptions and requirements in measurement in the social sciences. In J. A. Keats, R. Taft, R. A. Heath & S. H. Lovibond (Eds.), Mathematical and Theoretical Systems (pp. 7-16). North-Holland: Elsevier Science Publishers.

Wilson, M. (1989). A comparison of deterministic and probabilistic approaches to learning structures. Australian Journal of Education, 33(2), 127-140.

Understanding (or Misunderstanding?) the Rasch Model Cantrell, C.E. … Rasch Measurement Transactions, 1999, 13:3 p. 706

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt133i.htm

Website: www.rasch.org/rmt/contents.htm