Three Item Testing

With pre-calibrated items, only three items are needed to obtain useful estimates of population means on the same measurement scale as the items. Once a population mean is located relative to a set of known item calibrations, the population mean in raw score units on an entire instrument can also be determined. For studies in which the population parameters (measures or scores) are the main point of interest, this can mean huge savings in terms of time and money.

How is it possible to estimate population parameters without administering a complete instrument to a large sample? Data collected during the development of the Universal Nonverbal Intelligence Test (UNIT; Bracken & McCallum, 1997) and the Stanford-Binet Intelligence Test: Fourth Edition (Thorndike, Hagen, & Sattler, 1996) was used to investigate this question.

Any pair of items contains information about a population that answers them. Here is the performance of 9-year-olds on items 16 and 19 from the UNIT:

If most individuals in a population fail the pair of items, S₀₀, then the population mean is expected to be lower than the difficulty of the two items. Likewise, if the majority of a population pass a pair of items, S₁₁, then the population mean is expected to be higher than the difficulty of the items. Thus the ratio of S₁₁ to S₀₀ is related to the mean ability of the population on the entire test.

The other two cells, S₁₀ and S₁₀, reflect the difference in difficulty between the items. If Item 19 had been very easy and Item 16 very hard, most of the population would have fallen into cell S₀₁. Likewise, if Item 19 were hard and item 16 easy, most of the population would have been in cell S₁₀. In fact, the Rasch model predicts that log_e(S₁₀/S₀₁), the log-odds

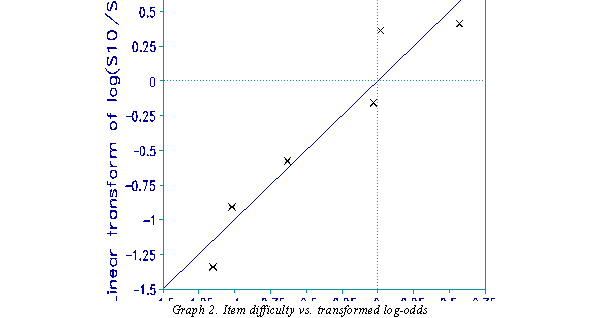
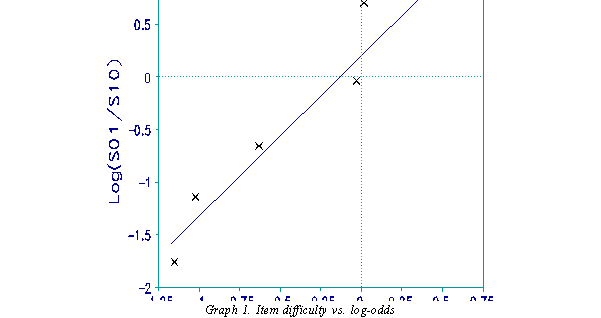
difference between the items, corresponds to their difference in difficulty. Graph 1 confirms this. Each point is the difference between the difficulty of a UNIT item and reference Item 19. The x-axis is the pre-calibration difference. The y-axis is the log-odds difference. The trace line is not the identity line because the scaling of the pre-calibrations is affected by other population and instrument characteristics. A simple linear transformation of the log-odds, however, places the points on an identity line (Graph 2).

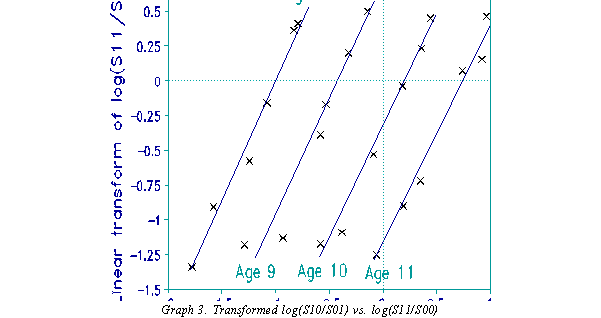
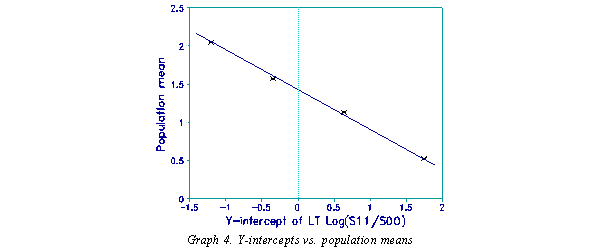
The same linear transformation is applied to the other ratio, log_e(S₁₁/S₀₀), so that all differences are on the measurement scale of the pre-calibrated items. Once this is done, plot the item difficulty differences, pre-calibrated or transformed log_e(S₁₀/S₀₁), against the transformed log_e(S₁₁/S₀₀) as in Graph 3. This graph yields x-intercepts which are reflect the population means. Graph 3 shows these plots for several different populations, while Graph 4 shows how the y-intercepts are related to the population means.

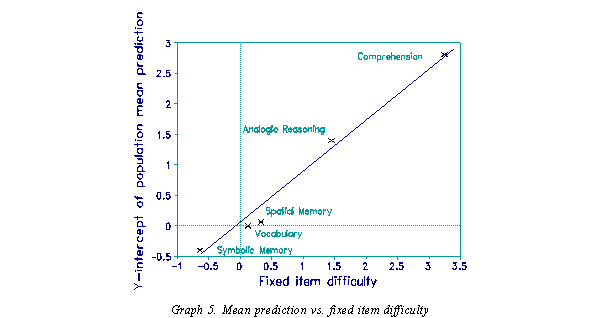
The formula for scaling the y-intercept of log_e(S₁₀/S₀₁) versus log_e(S₁₁/S₀₀) to the population mean is known in this case because the means are known. The slope of this line appears to be constant (m=-0.5) across multiple tests and populations. As graph 5 shows, the intercept is the difficulty of the constant item in the cross-tabs.

To summarize:

1. Administer three items from a calibrated test.

2. For two pairs of items (A,B and A,C) calculate the ratios, log_e(S₁₁/S₀₀) and log_e(S₁₀/S₀₁).

3. Linearly transform the two log_e(S₁₀/S₀₁) values to equal the A-B and A-C differences.

4. Apply the same linear transformation to the two log_e(S₁₁/S₀₀) values.

5. Estimate the y-intercept of the transformed log_e(S₁₁/S₀₀) versus transformed log_e(S₁₀/S₀₁) plot.

6. In our data, the y-intercept estimates the population mean as:

Kirk Becker
The Riverside Publishing Company

Bracken, B. A., & McCallum, R. S. (1998). The Universal Nonverbal Intelligence Test. Itasca, IL: Riverside.

Thorndike, R. L., Hagen, E. P., & Sattler, J. M. (1986). The Stanford­Binet Intelligence Scale--Fourth edition: Technical manual. Itasca, IL: Riverside.

Three Item Testing Becker, K. … Rasch Measurement Transactions, 2000, 13:4 p. 715

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt134a.htm

Website: www.rasch.org/rmt/contents.htm