Item Discrimination and Infit Mean-Squares

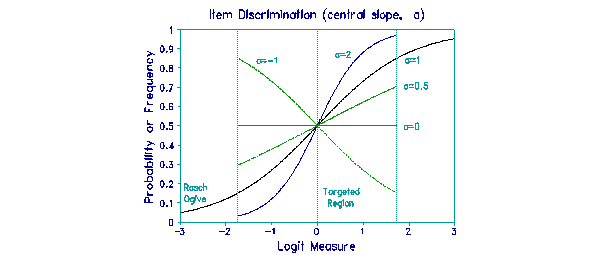
Descriptive approaches to item analysis parameterize differing central slopes in the empirical item characteristic curves (ICCs) as Item Discrimination, a. Rasch approaches detect differing slopes with quality-control fit statistics, most commonly the Infit mean-square (INFIT) statistic, an information-weighted chi-square statistic divided by its degrees of freedom. What is the numerical correspondence between INFIT and discrimination?

Before such an investigation can have meaning, obvious malfunctions in the data such as guessing, carelessness, data entry errors and mis-scoring are screened out. Then, Figure below shows various idealized ICCs, plotted in the region of the latent variable on which the item is targeted. The box covers the region equivalent to p=.15 to p=.85 of the Rasch ogive, i.e., -1.7 to +1.7 logits. Discrimination a=1 is the Rasch ogive for a dichotomous item, and is shown extending beyond the box. Empirical ICCs outside the box are better diagnosed by the Outfit Mean-square statistics and point-biserial correlation.

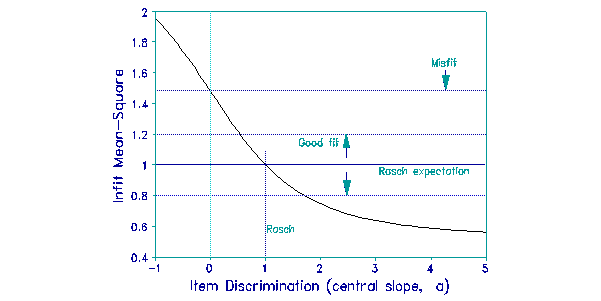
A simulation study produces the relationship shown in the Figure above. Central item discriminations from 0.5 to 1.7 produce good fit to the Rasch model, provided the part of the ICC away from the center is in reasonable conformance. This suggests that, for reasonably homogeneous items, empirical differences in item discrimination have no meaningful impact on measurement.

John Michael Linacre

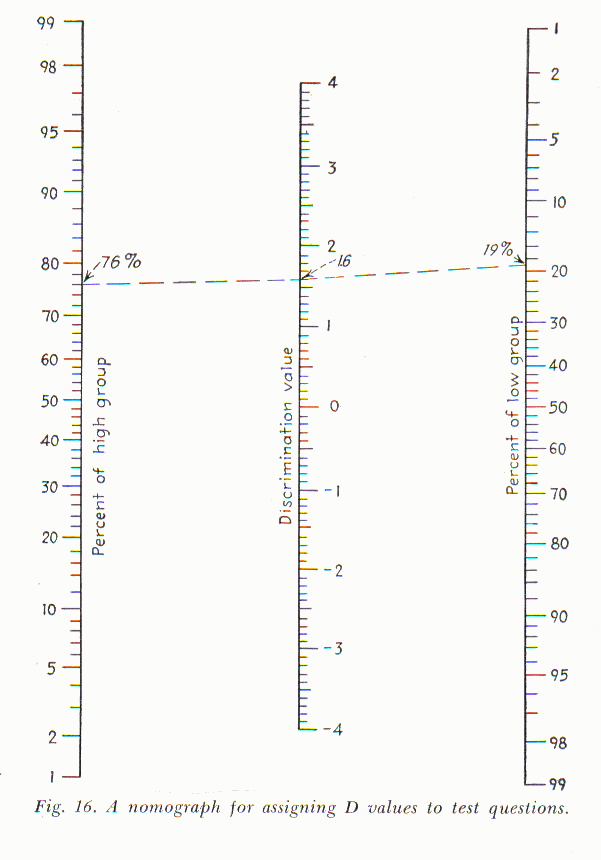
First, divide the sample into two strata (high and low). Second, compute the percentage of each strata succeeding on each item. Third, locate the two percentage points, one on each side of the nomograph. Fourth, the item discrimination is at the point where a line joining the two points crosses the middle line.
C.H. Lawshe, Jr. Principles of Personnel Testing. New York: McGraw-Hill, 1948, p. 190

Item Discrimination and Infit Mean-Squares. Linacre, J.M. … Rasch Measurement Transactions, 2000, 14:2 p.743

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt142a.htm

Website: www.rasch.org/rmt/contents.htm