Guttman Coefficients and Rasch Data

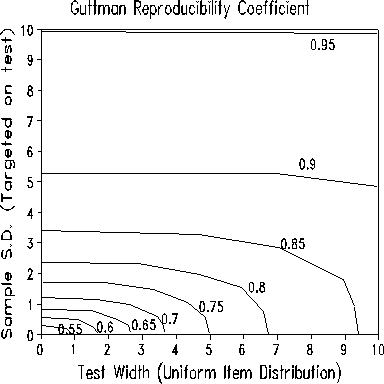
"I have been wondering if there has been any study on Guttman scaling (which is also known as implicational scaling in a number of sub-branches of linguistics) that looked at how likely it is, by sheer chance, to come up with a set of data that is highly reproducible (i.e., the coefficient of reproducibility is over .90) and also highly scalable (i.e., the Scalability Coefficient >> 0.60)."

Kenjiro Matsuda, Kobe Shoin Women's University, on the LINGUIST Forum.

The immediate answer to Matsuda's question is "highly unlikely". But to see why, let us go further and ask what are the expected values of the Guttman coefficients for various person and item dispersions, when the data fit a stochastic Guttman model, i.e., a Rasch model ("Rasch Model from Consistent Stochastic Guttman Ordering". RMT 6:3, p. 232).

On the LINGUIST Forum was also written:

"Guttman Scales are ones in which the items constitute a unidimensional series such that an answer to a given item predicts the answers to all previous items in the series (e.g., in an arithmetic scale, correctly answering a subtraction item predicts a correct answer to a prior item on addition, but not necessarily a later item on multiplication). That is, a respondent who answers an item in a positive way must answer less difficult items also in a positive way."

Coefficient of Reproducibility

Douglas W. Coleman, University of Toledo, writes:

"The coefficient of reproducibility measures how well we can predict any given student's responses from his/her position within the table; it should be at least .90."

The Coefficient of Reproducibility is:

C. of R. = 1 - Errors / (Total Responses)

First, sort the items (the columns) by item score, and persons (the rows) by person score, then display the responses as a table, called a Scalogram. For a perfect Guttman scale with no errors, the Scalogram will form a triangle of 1's (1 indicating a correct answer to the item) with no interior 0's and no exterior 1's (which would indicate passing a more difficult item but failing a less difficult one). A Guttman error is an interior 0 or an exterior 1 in the Scalogram.

Since, for practice, there is ambiguity in this definition, a convention, followed in SPSS-X and SAS (see RMT 5:4, p. 189), but not by Guttman or Menzel, is to act as though all persons with the same raw score are in the same row of the Scalogram, and all items with the same raw score are in the same column. (Guttman and Menzel sort the rows and columns opportunistically, apparently even regardless of their scores, in order to minimize the number of errors.)

The Figure above, from a simulation study, shows the results that can be expected when the data fit the Rasch model. The study indicates that C. of R. is essentially independent of test length or sample size (not shown here), but is influenced by test width and sample dispersion. It is seen that the benchmark number of 0.9 (Guttman, 1950) implies a wide sample.

Coefficients of Scalability

"The complete formula for the Coefficient of Scalability now reads: C. of S. = 1 - (Errors/Maximum Errors); where Maximum Errors is determined by whichever of the Maximum [Possible] Errors by Items [with fixed person marginals] and Maximum [Possible] Errors by Persons [with fixed item marginals] yields the smaller result."

Menzel, H. (1953) A new coefficient for Scalogram analysis. Public Opinion Quarterly, 17, 268-280.

and "The new level of acceptance [with C. of S.] may be somewhere between .60 and .65" (Menzel, p. 279)

But ...

"The scalability coefficient is defined as 1 minus the sum of the observed number of errors according to the Guttman scale model over the sum of the expected number of errors, assuming the responses to the items are independent across persons and the [item] marginals are fixed."

Debets, P., & Brouwer, E. (1989) MSP, a program for Mokken scale analysis for polychotomous items. Groningen, The Netherlands: ProGamma. (Following Loevinger, 1947, and Mokken)

A post to the LINGUIST Forum states that "C. of S. = 1 - (E/X), where E is the number of Guttman errors and X is the number of errors expected by chance", i.e., the second definition. It then adds: "By arbitrary convention, C. of S. should be .60 or higher to consider a set of items Guttman scalable."

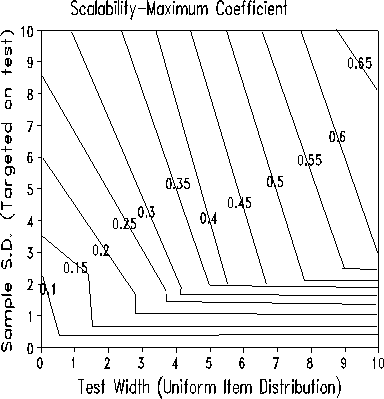
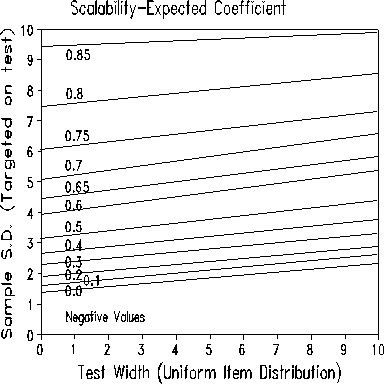
The two Figures above, again from a simulation study, show the expected values of the two scalability coefficients for "true/false" data that fit the Rasch model. It is seen that the two definitions yield very d different scalability coefficients. A major difference is that the "Maximum" Coefficient considers both persons and items, the "Expected" coefficient considers only items (according to my reading of the Guttman and Mokken literature). This disregard of the rows produces the counter-intuitive result that the wider the test, the lower the value of the "Expected" coefficient. We can the see that the benchmark value of 0.6 implies a wide test for the "Maximum" coefficient, but a wide sample for the "Expected" one.

Unfortunately, from the perspective of Rasch measurement, it appears that these coefficients have little to offer in evaluating data quality.

John Michael Linacre

Guttman, L. (1950) The basis for Scalogram analysis. In Stouffer et al. Measurement & Prediction, The American Soldier, Vol IV. New York: Wiley.

Loevinger, J. (1947) A systematic approach to the construction and evaluation of tests of ability. Psychological Monographs, 61, 4.

Mokken, R.J. & Lewis, C. (1982) A non-parametric approach to the analysis of dichotomous responses. Applied Psychological Measurement, 1982, 417-430.

Guttman Coefficients and Rasch Data. Linacre, J.M. … Rasch Measurement Transactions, 2000, 14:2 p.746-7

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt142e.htm

Website: www.rasch.org/rmt/contents.htm