Was the Rasch model Almost the Zermelo model?

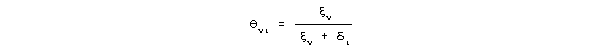
Here is Rasch's version of the familiar Rasch model: (Rasch, 1980, p. 168):

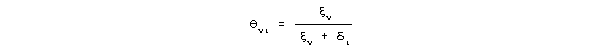
Here is Zermelo's (1929) model:

Both are multiplicative forms of the Rasch model. What is the difference? Rasch is contrasting persons with items. Zermelo is modeling paired comparisons. u_r and u_s are the strengths of two chess players. Zermelo notes that this model converts the strengths of the chess-players into probabilities, u_rs. These strengths are estimated from their tournaments scores. A draw is accommodated by adding 0.5 to the player's raw score. Zermelo omits to mention how he would use his model to predict draws. In current practice, the prediction of draws is facilitated by using a rating-scale model (RMT 11:3, p. 584). Zermelo, however, perceives that his model is robust against unplayed games (missing data) and able to accommodate linked tournaments! (Probably the first time these attributes of a Rasch model are noticed.)

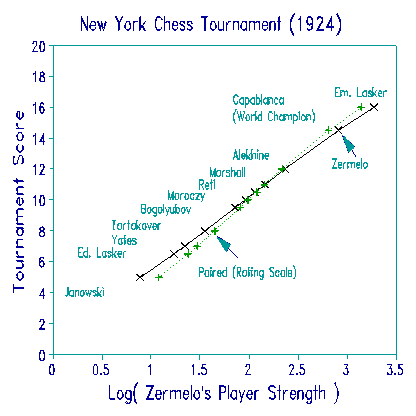
Why has Zermelo's model been ignored? His estimation technique is arduous, but worse, his explanation of the inferential meaning of the parameters is deficient. He fails to emphasize that u_r /u_s are the odds of success of player r relative to player s. Further, his paper lacks the fundamental insight that log_e(u_r) linearizes "Player strength", permitting the production of a useful picture. The Figure shows such a picture, plotted from Zermelo's own example analysis, which, we can see, lacks the drama which was present at the Tournament (Soltis, 1975). Zermelo's results are the same as those obtained using Facets with a dichotomous model and half-weighting of draws. A modern analyst, however, is more likely to use a rating scale model, so that draws can be predicted explicitly. For comparison, the player measures for a paired rating-scale model are shown in the Figure and are seen to differ little from Zermelo's estimates.

When Bradley and Terry (1952) independently formulated Zermelo's model, they observed that: "If the estimates are converted to logarithms, the values log_e [u_r] occur on a linear scale and permit overall comparisons of the experimental treatments [or chess players]. Any considerations of differences among treatments [or players] should be based on the values of the log [u_r]'s." (p. 326)

Bradley, R.A., and Terry, M.E. Rank analysis of incomplete block designs. I. The method of paired comparisons, Biometrika. 1952, 39, 324-45.

Soltis, A. (1975) The Great Chess Tournaments and Their Stories. Radnor, Pa.: Chilton.

Zermelo, E. (1929) The calculation of tournament results as a maximum-likelihood problem [German]. Mathematische Zeitschrift, 29, 436-460.

Was the Rasch model Almost the Zermelo model? Zermelo, E. … Rasch Measurement Transactions, 2000, 14:2 p. 754.

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt142k.htm

Website: www.rasch.org/rmt/contents.htm