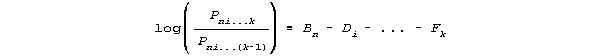Rating Scales, Disordering and Inferential Falsification

Andrich (1996) implies there are three levels of inferential validity inherent in a Rasch rating scale model: linearity, modality and decomposability.

1. Linearity without Decomposability
The construction of linear measures from ordinal data requires models resembling:

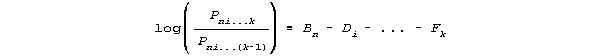
where P_ni...k is the probability that category k is observed when person n of ability B_n encounters item i of difficulty D_i. "..." represents other components of the measurement situation which intervene additively.

F_k is the difficulty of being observed in category k relative to category k-1, i.e., the step from category k-1 to category k. F_k corresponds to the position on the latent variable, relative to the item difficulty, at which categories k-1 and k are equally probable.

The estimate of F_k is dominated by the logarithm of the relative frequencies of the occurrence of categories k-1 and k in the data. Accordingly F_k may take any value from - to +. The derivation of a Rasch Rating Scale model from the standpoint of the measures implied by paired comparisons imposes no constraint on the {F_k} apart from that required for identifiability, which is conventionally F_k=0.

For usefully linear measures to be obtained from ordinal data, the data must approximate this model or one of similar form. The success of the approximation can be assessed by standard statistical techniques. In practice, however, "something is better than nothing", so the measures from even poorly fitting data are employed in preference to using raw scores or simply abandoning inference.

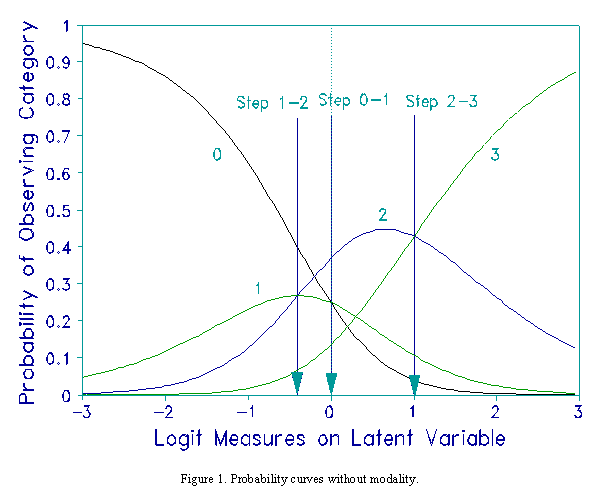
When F_k+1 is less than F_k, then the implication is that it is more likely that a higher category will be observed than the adjacent lower one, all else being equal. This is termed disordering. "... there is nothing ... that constrains [Rasch-Andrich] threshold estimates to be ordered ..." (Andrich, p. 20, his italics). Figure 1 illustrates this in terms of category probabilities. F₂, the step from category 1 to category 2 is less than F₁, the step from category 0 to category 1. Consequently category 1 is never a most likely, i.e., a modal, category.

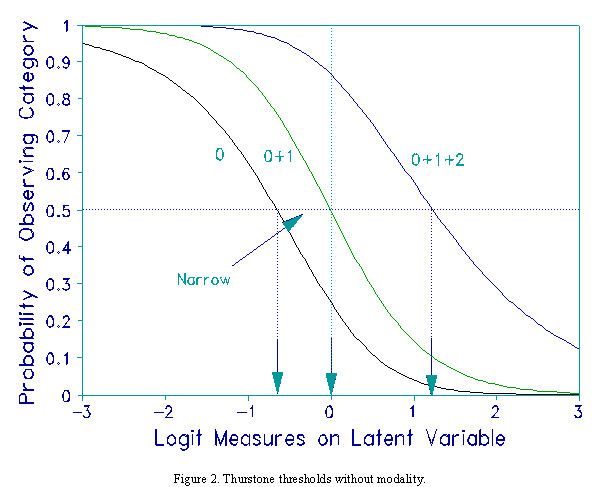
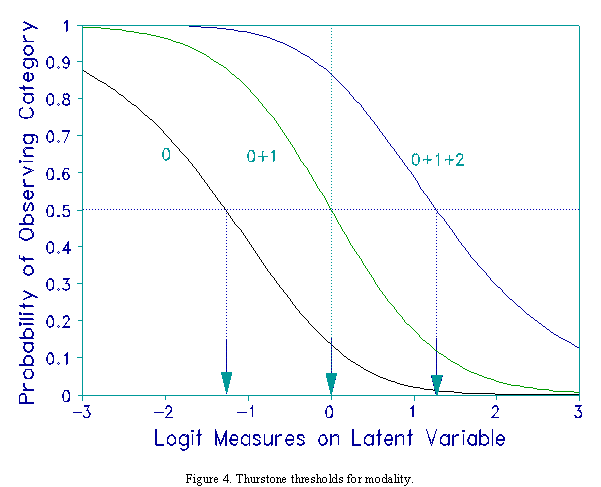
Disordering occurs because a category maps onto only a narrow interval on the latent variable. Figure 2 illustrates this in terms of Rasch-Thurstone thresholds. Category 1 is seen to occupy a rather narrow interval of the latent variable.

2. Modality or Dependent Decomposability
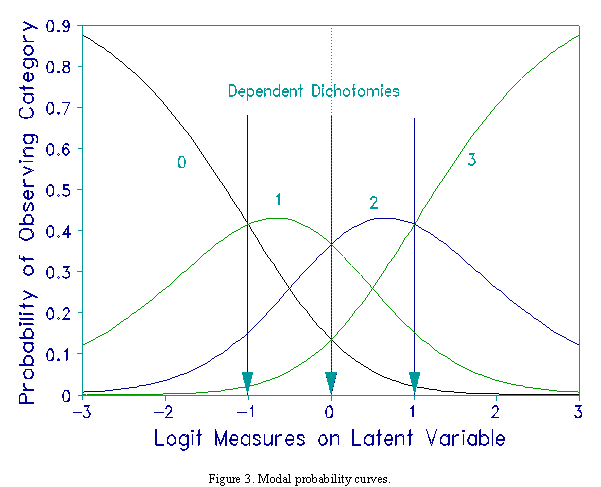
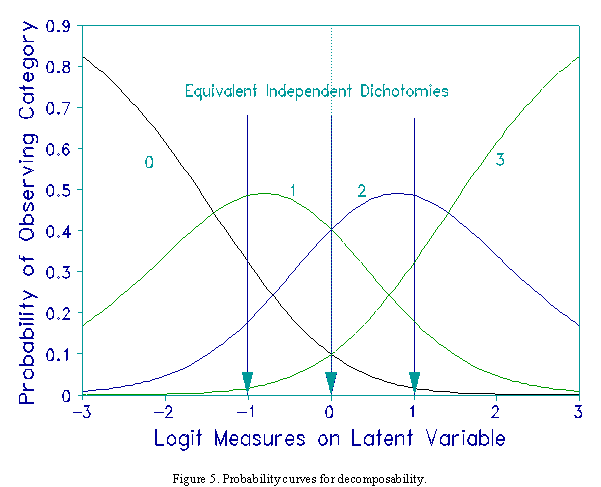
Andrich (p. 20) suggests "One hypothesis is that the [Rasch-Andrich] thresholds are ordered correctly." Correctly here means that the {F_k} have strictly ascending values. The implication of strict ascension is that each category in turn becomes modal on the latent variable. This is illustrated by the probability curves in Figure 3, in which the probability curves can be thought of as a "range of hills". Successive modality of categories has the inferential advantage that advances along the latent variable correspond strictly with advance in the category that is most likely to be observed. This facilitates communication and representation of the latent variable in terms of categories observed.

When modality is obtained, the categories can also be conceptualized as ordered dependent dichotomies. The dichotomies are located at the {F_k} and exhibit Guttman behavior, i.e., being observed in category k implies success on the kth and all earlier dichotomies. Figures 3 and 4 illustrate modality.

Andrich (p. 17) terms failure of the rating scale categories to exhibit successive modality as "falsification of the ordering of the categories". Of course, this is not a falsification of the substantive ordering of the categories, but on their failure to be ordered modally and so be representable as ordered dependent dichotomies. For instance, category 1, Disagree, may be rarely used on a particular survey, and so never modal on the scale "0=Strongly Disagree, 1=Disagree, 2=Agree, 3=Strongly Agree". Thus it is reported that the "ordering of the categories is falsified". This does not mean that Disagree implies more disagreement than Strongly Disagree, or more agreement than Agree. It merely implies that Disagree is rarely observed and so corresponds to a narrow interval on the latent variable.

3. Independent Decomposability
Andrich (p. 17) suggests the possibility of an even stricter criterion, that the rating scale be conceptualized as "independent dichotomous decisions". If a rating scale can be decomposed mathematically into independent dichotomies, then each dichotomous decision point can be identified with a conceptually independent location on the variable, further simplifying communication. This occurs transparently when a raw score on a multiple-choice test is treated as an ordinal category on a rating scale corresponding to the length of the test.

The mathematical requirements for a rating scale to be decomposable into dichotomies are complex (Huynh 1996), but, for practical purposes, unless each F_k is at least 1.4 logits greater than its predecessor, the rating scale is not decomposable. Figures 4 and 5 illustrate a decomposable rating scale.

John Michael Linacre

Andrich DA (1996) Measurement criteria for choosing among models with graded responses. Chapter 1 in A. von Eye & C.C. Clogg, Categorical Variables in Developmental Research. San Diego: Academic Press.

Huynh H (1996) Decomposition of a Rasch partial credit item ... Psychometrika 61:1 31-39.

Rating Scales, Disordering and Inferential Falsification. Linacre J.M. … Rasch Measurement Transactions, 2001, 15:1 p.795-7

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt151j.htm

Website: www.rasch.org/rmt/contents.htm