| |
Generalizability Theory
|
Rasch Measurement
|
| Purpose: |
Generalize, from observed raw scores or
responses, "universal" raw scores or responses.
Reduce unwanted variance in future studies. |
Construct, from observed responses, linear
measures for each facet element free of other facet
distributions.
Assess quantitative validity of each measure. |
| Inference: |
Relative decisions, ignoring decision-neutral
variance. Absolute decisions, including all
variance. |
Linear measures with standard errors (precision),
fit statistics (validity).
Frame of reference is criterion by items and
normative by persons. |
| Analysis stages: |
Generalizability: Collection and analysis of
data from which to generalize.
Decision: G-study results used to evaluate error
minimization and resource optimization
alternatives in future research. |
Test conceptualization: Model enables verifying
rating plan validity and estimating measurement
precision prior to, during and after data collection.
Measurement: Construction and statistical
validation of measures from data. |
| Data: |
Raw scores or responses. |
Raw responses. |
| Context: |
Universe of admissible observations that test-user accepts as interchangeable. |
All responses intended to manifest measures on
the same variable. |
| Data modelled as: |
Linear combination of context effects. |
Ordinal stochastic manifestation of linear
parameters. |
| Typical model: |
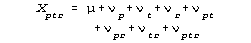
Xptr is observed datum.
v.. are context effects: p for persons,
vt for items, r for raters, etc
vptr is residual error. |
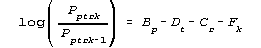
Pptrk probability of observing category k.
Bp, Dt, Cr are latent parameters: Bp is person
measure, Dt is item difficulty, Cr is rater severity
Fk quantifies rating scale non-linearity |
| Measurement target: |
Object of measurement (e.g., persons) and their
universe score variance. |
Measures for all parameters. |
| Facet: |
Aspect of situation (item, rater, time, but not
object of measurement), represented by its conditions (items, raters, times).
Each facet, generalized to the universe from its conditions, is a source of universe score
measurement error in the object of measurement. |
Any component of situation (person, item, rater,
time) containing its elements (persons, items,
raters, times).
Measure, error and fit statistics are estimated for
every element of every facet,as well as for every
specified element group within each facet. |
| Facet types: |
Random: Observed conditions are random,
exchangeables sampled from the facet universe
(e.g., raters represent all raters).
Fixed: Observed conditions are the universe
(e.g., this test has all items of interest). |
Measurement: Facet elements interact to cause
data (persons, items, raters).
Analysis: Measured elements are summarized or
decomposed according to other facets (sex,
ethnicity, item type).
Fixed effect: Facet elements replicate a fixed
effect (community attitude to new highway),
individual elements are not parameterized. |
| To work
successfully: |
At least one facet of random error. |
All elements of all facets must be linked in the
data or by constraints. |
| Assumptions: |
Error distributions remain fixed.
Items retain difficulty variance. |
Measurement structure remains fixed.
Facets retain construct validity. |
| Valid rating plans: |
Fully crossed: all conditions of each variance
source observed with all conditions of all other
sources.
Crossed: all conditions of one facet observed
with all conditions of another variance source.
Nested: two or more conditions of nested
variance source appear with only one condition
of another facet.
Partially nested: some conditions of nested
variance source appear with some conditions of
another facet. |
Implicit Links: Data network links all elements
of all facets such that all measures can be
estimated unambiguously in one frame of
reference.
Explicit Constraints: Relations between unlinked
elements (New York and Oregon) are specified
(New York and Oregon tests said to be equally
difficult, or New York and Oregon students said
to be equally able). |
| Estimation: |
Analysis of variance.
Restricted maximum likelihood.
Minimum variance quadratic estimation. |
Logit-linear maximum likelihood.
Least-squares. |
| Estimates: |
Variance components. |
Measures, errors, fits. |
| Ideal datum for
measurement: |
Object of measurement's mean score over all
acceptable observations. |
Sufficient responses for each element to estimate
its parameter. |
| Ideal test: |
Item difficulties are all equal. |
Item difficulties range across person abilities. |
| Effect of widening
item difficulty
range: |
More variability.
Less generalizability.
Reported as item condition variance. |
More measure range.
Slightly less measure precision.
Reported as item calibration variance. |
| Ideal raters: |
Identical rating machines. |
Self-consistent.
Shared understanding of rating scale. |
| Effect of severe
rater: |
More variability.
Less generalizability. |
No effect. |
| Effect of
interaction: |
More variability.
Less generalizability.
Reported separately or as residual variance. |
Less fit, reported by fit stats.
Motivates: DIF inquiry, test modification, bad
data removal, better rater instruction, etc. |
| Effect of random
and unidentified
variance: |
More variability.
Less generalizability.
Reported as residual variance. |
Reported in measure standard errors. Uneven
stochasticity reported by fit stats. Individual
improbable responses reported. |
| Departure from
ideal quantified
by: |
Dependability of generalizing from observed to
universe object of measurement score.
Generalizability is overall dependability. |
Precision measured by Standard Errors.
Quantitative validity measured by Fit Stats.
Utility measured by facet-element separation. |
| Diagnosis of data-model failure: |
Large residual error term.
Low generalizability. |
Large misfit or lack of construct validity indicate
some data do not support measurement. |
| Analysis results: |
Variance table, e.g., Shavelson & Webb, p. 102,
Table 7.2 |
Construct map. |