Lessons from Thermometry

Why be concerned about how an instrument is calibrated?:
"First, because an appreciation of the means of calibration and the precautions necessary to obtain accuracy should enable the user to take better advantage of his instrument where the highest accuracy is needed. In any event, a study of the precautions which have to be taken in the accurate calibration of instruments should provide some guide as to suitable means for minimizing errors in the practical measurement of temperature."
Quotations are from: National Physical Laboratory (1955) Calibration of Temperature Measuring Instruments. London: HMSO, p. 2ff.

"Secondly, because it may encourage him to accept, where this is appropriate, a lower standard of accuracy, with improved speed and less cost, perhaps by adapting testing methods in a simple form to his own problem."

"Finally, there is the intrinsic scientific interest of the problems involved in establishing and reproducing a scale of temperature."

Prerequisites to calibration:
"Before any temperature measuring instrument can be calibrated, there are three fundamental factors which must be taken into consideration: (i) the temperature scale to be used; (ii) the required accuracy of the calibration, and (iii) the choice of method and apparatus."

Difficulties in constructing a scale:
"Unfortunately, a fundamental scale of temperature is not very easily realized, and, as will be shown later, a considerable amount of work is necessary in order that such a scale may be uniquely defined. It is essential that whatever scale is adopted should be sufficiently reproducible to satisfy all likely requirements of accuracy."

Choosing the instrument to calibrate?
"The accuracy of the calibration of a particular instrument depends on the accuracy desired by the user and the accuracy of which the instrument is capable. The method of test is normally chosen so as to satisfy the user's requirements, but preliminary calculation and past experience may show that the readings of the instrument are not, in fact, sufficiently dependable to give the required accuracy, so that the user may be faced with the alternatives of accepting a lower accuracy or of adopting some other type of instrument for his measurements."

The practical problems of instrument equating:
"The temperature scale which is most familiar is that which appears on the ordinary mercury-in-glass thermometer. In an ideal instrument of this type, each graduation on the stem of the thermometer would correspond to an equal increase in the volume of mercury relative to the glass in which it is contained. Suppose we have two such ideal thermometers, identical in all respects except that they are made of different types of glass, and both divided so that they read 0 in melting ice and 100 in the vapor of water boiling under normal atmospheric pressure. If these two thermometers were subjected to a temperature somewhere midway between 0 and 100 they would not necessarily read the same. For example, if one thermometer were made from Jena 16 glass and read exactly 50, and the other were made of Jena 59 glass the latter would read about 49.92. That is, the two thermometers would define different temperature scales."

"Temperature" is a an idealized fiction!
"In fact, if the change in any physical property of any real substance is taken as a measure of temperature, the scale of temperature so defined is peculiar to that substance, and has no general theoretical significance. ... Such a scale cannot be realized directly in practice, and the usual way of arriving at a fundamental scale is to make measurements with a gas thermometer and to apply the corrections necessary to allow for the measured departures from perfection of the particular gas used."

"Absolute zero" is a fiction, independent of the properties of any real substance
"Consider the case of the volume of a gas. If we have a certain mass of gas occupying unit volume at 0C, and we take our temperature scale such that the freezing and boiling points of water are numbered 0 and 100 (that is, we adopt the Celsius or Centigrade scale), then, if we cool the gas by 1 its volume will be reduced by about 1/273 of its volume at 0C, and so on, in a linear fashion over a wide range of temperature, Clearly, if this law held over an indefinite range of temperature, by the time we reached a temperature of -273C the gas would cease to have any volume. However, before this temperature is reached any real gas will have become a liquid, and before that stage is reached, departures from the simple linear law will have become appreciable. Measurement of these departures enables us to compute what would have been the behavior of a "perfect gas" and we find that such a gas would cease to have any volume at a temperature of about -273.15C. This temperature is known as the absolute zero, and the scale defined by this perfect gas is independent of the properties of any real substance. This scale can also be shown to be identical with the "thermodynamic scale" defined by Kelvin in terms of the work done by a perfect heat engine operating between two temperatures, the temperature interval being proportional to work done."

Accuracy vs. reproducibility [=reliability]
"Unfortunately, a gas thermometer is not a convenient instrument to use, and, even worse, it is not capable of such a high degree of reproducibility of reading as is required for many purposes. On the other hand there are available temperature measuring instruments capable of a very high degree of reproducibility, and the use of these enables us to reproduce a temperature to a high degree of accuracy, even though we may not know its value so closely on the thermodynamic scale. We have, therefore, to draw a distinction between accuracy and reproducibility in temperature measurement."

Practical calibration of thermometers:
"In order to take advantage of the fact that we can reproduce a scale much more accurately than we can define it absolutely, all nations signatory to the Convention du Mètre have agreed on an International Temperature Scale. This scale is based on a number of fixed points, each of which has been the subject of reliable gas thermometer observations, and these are then linked by interpolation, using the instruments which offer the highest degree of reproducibility. In this way the International Temperature Scale is conveniently and accurately reproducible and provides means for identifying any temperature within much narrower limits than is possible on the thermodynamic scale."

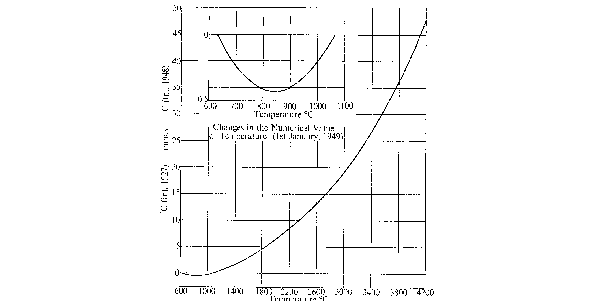
Maintaining the Temperature Scale:
"The scale was originally specified ... in 1927.... In 1948 certain changes were made, with the result that on the 1948 scale most temperatures are denoted by numerical values slightly different from those which would have been required by the 1927 scale. The differences are given in the figure and it will be seen that, for temperatures up to at any rate about 2000C, the changes are scarcely outside the normal limits of experimental error. For work of high precision, however, the scale which has been used must be specified. For example 800C (Int. 1927) is the same temperature as 800.4C (Int. 1948)."

Scale drift and deterioration: requirement to recalibrate instruments
"It is clear that the maintenance of [benchmark] standards of temperature requires a great deal of care and vigilance, for the standards are exceptionally liable to change or deteriorate by the mere fact of being used. The deterioration may be slow or rapid, according to the type of instrument and the temperatures involved, but, even if it is slow, it is none the less insidious."

"Deterioration is likely to be even more serious with instruments which are in regular use in industrial or research applications, and it is therefore very desirable that users of temperature-measuring instruments should be equipped to make regular routine checks of accuracy."

Lessons from Thermometry. National Physical Laboratory … Rasch Measurement Transactions, 2001, 15:1 p.810-11

Rasch Books and Publications
Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, 2nd Edn. George Engelhard, Jr. & Jue Wang	Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan
Other Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt151v.htm

Website: www.rasch.org/rmt/contents.htm