Standardized Mean-Squares: RUMM2010 and Winsteps

The normal distribution underlies most statistical theory. "Everyone believes in the normal law, the experimenters because they imagine it is a mathematical theorem, and the mathematicians because they think it is an experimental fact." (Gabriel Lippman, in Poincaré's Calcul de probabilités, 1896). But the normal distribution is a useful fiction. It describes the situation that would occur were there to be infinitely many, infinitely small fluctuations around some precise "true" value. We might imagine, for instance, that if the unexpectedness in a subject's response matches a prescribed normal distribution, then we have no need for further investigation.

Each subject's response to an item contains some amount of unexpectedness. The Rasch model predicts a certain amount of unexpectedness. We can compare these two unexpectednesses and compute a normal deviate. This deviate is the location in a unit normal distribution that has the same amount of unexpectedness as the subject's response.

As a subject takes more and more items, or an item is taken by more and more subjects, we can accumulate more and more normal deviates. If the distribution of observed unexpectedness matches the model-predicted unexpectedness distribution then our inclination is to imagine that the data accord with the Rasch model. But how are we to check this? There are infinitely many ways that an observed distribution can depart from a theoretical one.

One major departure is that the observed distribution has too much or too little variance. We can sum the squares of the normal deviates and compare this sum with its model predicted value. The sum has a chi-square distribution and its model-predicted value is its degrees of freedom, here the number of observations. When we divide a chi-square statistic by its degrees of freedom we obtain a mean-square statistic with an expected value of 1.0. When the mean-square value is less than 1.0 then the data are too predictable, i.e., information-deficient. When the mean-square is greater than 1.0 then there is too much unexpectedness, i.e., noise. This mean-square is called the "Fit MnSq" in Best Test Design, the "Unweighted Mean Square" in Liking for Science, and the "OUTFIT MNSQ" in Winsteps.

How far away does a mean-square need to be from 1.0 before we are concerned about it? There are two approaches: the substantive and the statistical. The substantive question states: "Is the departure big enough to impair the utility of the measures?" The statistical question states: "Is the departure so big that it is unlikely to occur when the data fit the model?"

Experience indicates that the substantive question is more relevant to every-day decision making, but let's answer the statistical question here. The mean-square itself has an expectation of 1.0 and a model-predicted variance. Consequently, the observed value of a mean-square can be converted, i.e., "standardized", into a unit normal deviate. If the unit normal deviate is unusually large or small, then it is likely that some of the data do not accord with the Rasch model. As data sets get larger, we are more likely to detect inevitable deficiencies, so that standardized statistics tend to loose their meaning. A "standardized" normal deviate (t or z) is called a "Fit Statistic t" in Best Test Design, an "Unweighted Fit t" in Liking for Science, an "OUTFIT ZSTD" in Winsteps, and a "Residual" in RUMM2010.

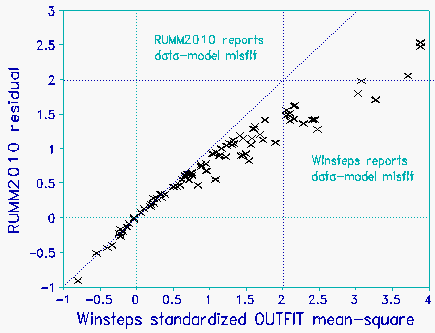
The Figure plots standardized statistics for RUMM2010 and Winsteps for the same data. From the Figure one might conclude: "Winsteps is more sensitive to misfit," or "RUMM2010 produces estimates that fit the data better." Both conclusions would be incorrect. For these data, RUMM2010 and Winsteps produce identical measures and standard errors. The plot depicts the effect of subtle differences in the choice of mean-square computations and standardizations.

John Michael Linacre

Standardized Mean-Squares. Linacre J.M. … Rasch Measurement Transactions, 2001, 15:1 p.813

Rasch-Related Resources: Rasch Measurement YouTube Channel
Rasch Measurement Transactions & Rasch Measurement research papers - free	An Introduction to the Rasch Model with Examples in R (eRm, etc.), Debelak, Strobl, Zeigenfuse	Rasch Measurement Theory Analysis in R, Wind, Hua	Applying the Rasch Model in Social Sciences Using R, Lamprianou	El modelo métrico de Rasch: Fundamentación, implementación e interpretación de la medida en ciencias sociales (Spanish Edition), Manuel González-Montesinos M.
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Rasch Models for Measurement, David Andrich	Constructing Measures, Mark Wilson	Best Test Design - free, Wright & Stone Rating Scale Analysis - free, Wright & Masters
Virtual Standard Setting: Setting Cut Scores, Charalambos Kollias	Diseño de Mejores Pruebas - free, Spanish Best Test Design	A Course in Rasch Measurement Theory, Andrich, Marais	Rasch Models in Health, Christensen, Kreiner, Mesba	Multivariate and Mixture Distribution Rasch Models, von Davier, Carstensen
Rasch Books and Publications: Winsteps and Facets
Applying the Rasch Model (Winsteps, Facets) 4th Ed., Bond, Yan, Heene	Advances in Rasch Analyses in the Human Sciences (Winsteps, Facets) 1st Ed., Boone, Staver	Advances in Applications of Rasch Measurement in Science Education, X. Liu & W. J. Boone	Rasch Analysis in the Human Sciences (Winsteps) Boone, Staver, Yale	Appliquer le modèle de Rasch: Défis et pistes de solution (Winsteps) E. Dionne, S. Béland
Introduction to Many-Facet Rasch Measurement (Facets), Thomas Eckes	Rasch Models for Solving Measurement Problems (Facets), George Engelhard, Jr. & Jue Wang	Statistical Analyses for Language Testers (Facets), Rita Green	Invariant Measurement with Raters and Rating Scales: Rasch Models for Rater-Mediated Assessments (Facets), George Engelhard, Jr. & Stefanie Wind	Aplicação do Modelo de Rasch (Português), de Bond, Trevor G., Fox, Christine M
Exploring Rating Scale Functioning for Survey Research (R, Facets), Stefanie Wind	Rasch Measurement: Applications, Khine	Winsteps Tutorials - free Facets Tutorials - free	Many-Facet Rasch Measurement (Facets) - free, J.M. Linacre	Fairness, Justice and Language Assessment (Winsteps, Facets), McNamara, Knoch, Fan

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt151x.htm

Website: www.rasch.org/rmt/contents.htm