Likelihoods, Scores and Measures

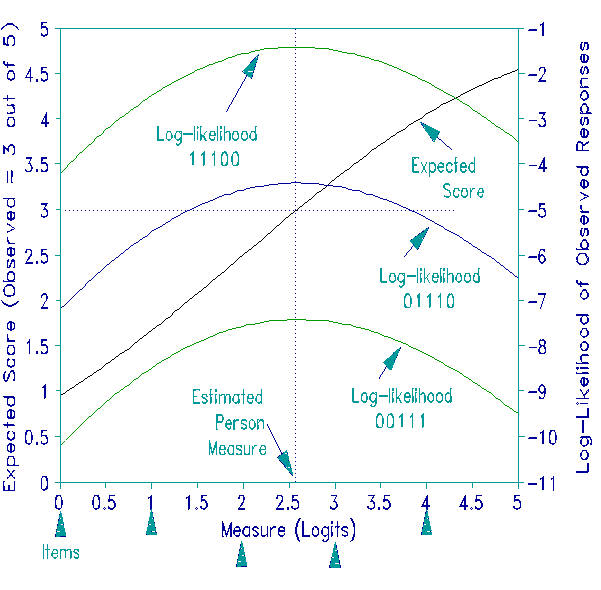
What is the "correct" estimate of a person's ability? Whatever the method used to estimate item difficulties, person measures are estimated as though the item difficulties are exactly known. But we can imagine several bases for estimation.

What is the ability for which a person's set of responses is most likely to be observed? R. A. Fisher proposed this approach. In the Figure below, there are 5 items of logit difficulties, 0, 1, 2, 3, 4. The target person has a score of 3 out of 5. The likelihood of this score is the product of the probabilities of the responses made by the person. Different response strings "11100", "01110", "00111" have different likelihoods for a person of a particular ability. For a person of low ability, any of these response strings is very unlikely, similarly for a person of high ability. Somewhere in the middle of the ability range, these likelihoods will reach their peaks.

Since likelihoods are numbers very close to zero, it is convenient to take their logarithms and express them as negative numbers. The Figure shows a surprising feature of the Rasch model. The log-likelihoods, and so the likelihoods, of all three response strings (and all similar ones) have their maxima at the same measure! 2.6 logits is the person ability estimate given by the Method of Maximum Likelihood.

Another approach, paralleling Gaussian least-squares, is to estimate the ability measure to be the measure at which the squared difference between the observed and expected score for the person is minimized. We can, in fact, reduce this difference to zero. The observed score is 3 out of 5. A low measure would predict a score less than 3, a high measure a score higher than 3. Somewhere a measure would exactly predict 3. The Figure shows that this occurs at a person ability estimate of 2.6 logits. Surprisingly, but conveniently, this is the same as the maximum likelihood estimate. This coincidence is a feature of the mathematical properties of the Rasch model.

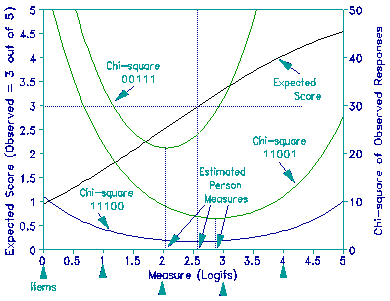
A third approach is to estimate the ability measure to be the value which gives the best fit according to some fit statistic. The second Figure shows the abilities estimated from three response strings based on minimizing a chi-square fit statistic. It is seen that different ways of making the same raw score yield different measures. Though this approach to estimation has a rich history, going back at least to Yule (1925), there is an arbitrariness in the choice of fit statistic, and an indeterminacy in the measure corresponding to a "score", that contradict the usual concept of "measurement."

John M. Linacre

Yule G.U. (1925) The growth of population and the factors which control it. Presidential address. Journal of the Royal Statistical Society 88 1-62 (261)

Likelihoods, Scores and Measures Linacre, J.M. … Rasch Measurement Transactions, 2001, 15:2 p. 815-6

Rasch Publications
Rasch Measurement Transactions (free, online)	Rasch Measurement research papers (free, online)	Probabilistic Models for Some Intelligence and Attainment Tests, Georg Rasch	Applying the Rasch Model 3rd. Ed., Bond & Fox	Best Test Design, Wright & Stone
Rating Scale Analysis, Wright & Masters	Introduction to Rasch Measurement, E. Smith & R. Smith	Introduction to Many-Facet Rasch Measurement, Thomas Eckes	Invariant Measurement: Using Rasch Models in the Social, Behavioral, and Health Sciences, George Engelhard, Jr.	Statistical Analyses for Language Testers, Rita Green
Rasch Models: Foundations, Recent Developments, and Applications, Fischer & Molenaar	Journal of Applied Measurement	Rasch models for measurement, David Andrich	Constructing Measures, Mark Wilson	Rasch Analysis in the Human Sciences, Boone, Stave, Yale
in Spanish:	Análisis de Rasch para todos, Agustín Tristán		Mediciones, Posicionamientos y Diagnósticos Competitivos, Juan Ramón Oreja Rodríguez

Forum

Rasch Measurement Forum to discuss any Rasch-related topic

Go to Top of Page
Go to index of all Rasch Measurement Transactions
AERA members: Join the Rasch Measurement SIG and receive the printed version of RMT
Some back issues of RMT are available as bound volumes
Subscribe to Journal of Applied Measurement

Go to Institute for Objective Measurement Home Page. The Rasch Measurement SIG (AERA) thanks the Institute for Objective Measurement for inviting the publication of Rasch Measurement Transactions on the Institute's website, www.rasch.org.

The URL of this page is www.rasch.org/rmt/rmt152a.htm

Website: www.rasch.org/rmt/contents.htm